织物拉伸弹性回复率与其力学性能的关系

赵立环，王兵兵

（天津工业大学 纺织学部，天津 300387）

织物拉伸弹性回复率与其力学性能的关系

赵立环，王兵兵

（天津工业大学 纺织学部，天津 300387）

为探究较精确、易行的测试表征和改善织物拉伸弹性回复性的方法，首先采用KES-F织物风格仪测试了织物的弯曲、剪切、拉伸和压缩性能，并在KES系统原有力学性能指标基础上引入两个新指标：残余弯曲曲率和残余剪切变形，通过数据分析分别建立了采用织物力学性能指标表示其拉伸弹性回复率和反复拉伸弹性回复率的回归方程；同时分析了织物拉伸弹性回复率和反复拉伸弹性回复率与各力学性能指标间的相关性.结果表明：在置信度区间95%条件下，拉伸弹性回复率均可由各力学性能指标的回归方程计算得到；拉伸功回复率和剪切刚度对织物拉伸弹性的影响最大，可以通过提高织物的拉伸功回复率及剪切刚度来改善织物的拉伸弹性回复性.

织物；拉伸弹性回复率；力学性能；回归方程；相关性

织物的拉伸弹性回复性反映了在规定条件下对织物施加拉力和卸除负荷后，拉伸变形能一定程度回复的织物性能.织物拉伸弹性回复性对弹性服装的外观风格及穿着舒适性起至关重要的作用，该性能的优劣在某种程度上直接决定弹性面料及其服装的品质与档次.因此面料与服装设计师在设计弹性面料及其服装时所关注的织物重要性能之一就是拉伸弹性回复性.目前，对织物拉伸弹性回复性的评价，主要是通过测试织物的拉伸弹性回复率和反复拉伸弹性回复率来分别衡量其单次拉伸弹性回复性和抗多次拉伸的疲劳变形性能，测试方法参照 FZ/T 01034-2008——纺织品机织物拉伸弹性实验方法；该方法在实际测试中应用较为广泛，但是其存在工作量大、试样耗费量大等缺点.另外，目前鉴于工厂在开发弹性面料时，需要反复的试纺、试织试验，从而造成人力、财力以及材料浪费的事实，迫切需要一种弹性面料的开发指导方法.因此，本文拟探索一种易操作、测量数据较精确且稳定的评价织物拉伸弹性回复性的方法，同时找出一种改善织物弹性回复性的途径.在前期研究中，发现织物拉伸弹性实质上是织物多种变形的综合体现[1-3]，织物的拉伸弹性回复性能与织物的力学性能指标之间必然存在一定的关系[4-5]，且未查到有关织物拉伸弹性回复性与其力学性能指标间关系的研究报道.在相关研究领域，张晓婷等[6-7]研究过织物弹性中的折皱弹性（即折皱回复性）与其物理力学性能指标间的关系；赵立环等[8]在张晓婷等人的研究基础上，进一步完善了织物折皱回复性与其力学性能指标间的关系研究.本文将在前期研究[8]的基础上，进一步研究织物的拉伸弹性回复性与其力学性能指标间的关系.

1 实验部分

1.1 样品准备

为了使实验结果具有代表性，从天纺投资控股有限公司收集了20块纬弹弹力布样品，包含多种原料（棉、锦纶、氨纶、陶氏纤维、PTT、涤纶、甲壳素、竹纤维、纽代尔）.样品均是经过染前和染色处理的织物，具体样品规格如表1所示.

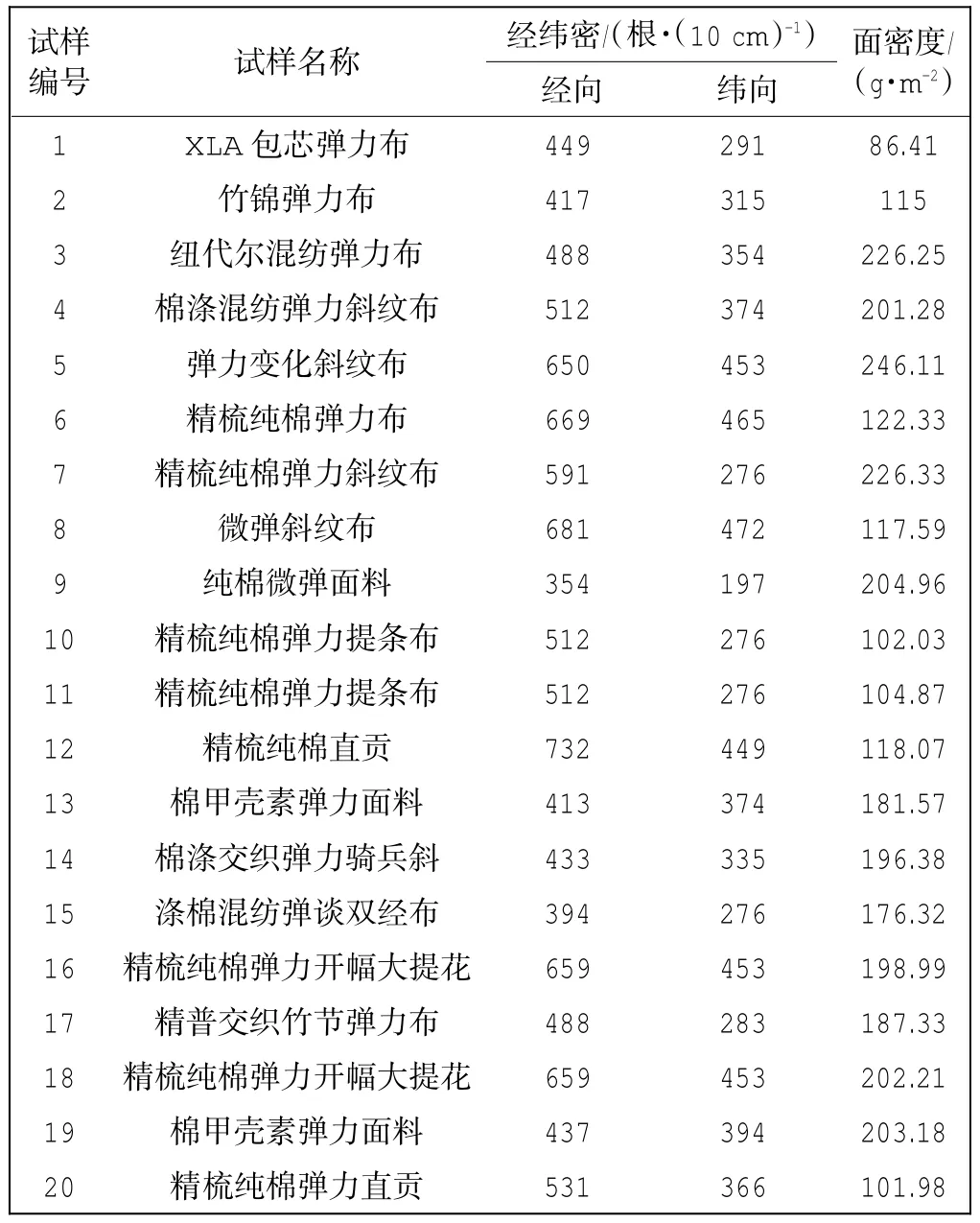
表1 样品规格Tab.1 Specifications of samples

1.2 实验过程

本实验采用KES-FB川端织物风格仪（KATO TECH CO.，LTD产品）测试各样品的力学性能指标.由于仪器较为精密，对试样平整度要求较高，因此为保证数据的精确度，试验前对有折痕的织物进行低温熨烫，以确保各样品的平整性.实验过程如下：①在距布边5 cm以上的位置，分别从样品的经、纬向各剪取试样3块（试样大小：20 cm×20 cm），然后使试样在恒温恒湿室内调湿24 h（温度为（20±2）℃，相对湿度为65%±3%）；②打开仪器，首先预热30 min，然后按照仪器操作规程开始实验，每种力学性能各测试样品的经、纬向试样各3块，依次进行压缩实验（FB-3）、纯弯曲实验（FB-2）和拉伸与剪切实验（FB-1）.

织物拉伸弹性回复率测试实验过程如下：①在恒温恒湿室（温湿度同上）内，按照FZ/T01034-2008的测定方法标准，从各样品的纬向分别剪取试样3块，试样长宽尺寸：200 mm×50 mm，并调湿24 h；②按照操作规程设置25 N的定力，将试样夹持在试样夹上，并施加0.3 N的预加张力；③启动INSTRON万能强力机，在100 mm/min的速率下拉伸试样至定力，并保持其定力1 min后读取试样长度L1，然后以相同速率使夹钳回复零位，停置3 min；④再以相同速率拉伸试样至规定的预张力0.3 N，读取试样长度L2.对于定力反复拉伸，采用10次循环次数，按照步骤②和③反复拉伸，至预定循环次数后，测其长度L1；再按步骤④测其长度L2.最后按①式计算每块试样的定力弹性回复率和定力反复拉伸弹性回复率.

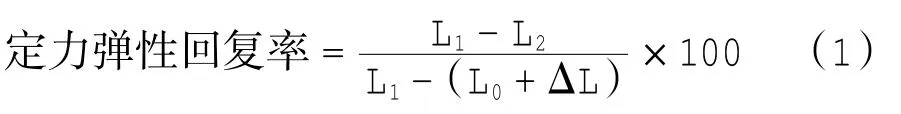
式中：L0为隔距长度（mm）；L1为试样拉伸至定力保持1 min后的长度（mm）；L2为试样回复至零位停置3 min后再施加预张力时的长度（mm）；ΔL为松式夹持试样时达到预张力时的伸长（mm）.

1.3 实验结果

实验结果如表2所示.

表2中包括织物拉伸弹性回复率D（%）、弯曲刚度B（cN·cm2·cm-1）、弯曲滞后矩H（cN·cm·cm-1）、残余弯曲曲率K（cm-1）、剪切刚度G（cN·（cm·（°））-1）、剪切角为0.5°时的剪切力滞后量H0.5°（cN·cm-1）、剪切角为5°时的剪切力滞后量H5°（cN·cm-1）、残余剪切变形Φ（°）、拉伸线性度L、拉伸比功P（cN·cm·cm-2）、拉伸功回复率R（%）、压缩线性度PL、压缩比功PP（cN·cm· cm-2）、压缩功回复率PR（%）.每块样品的拉伸弹性回复率均为取3块试样的平均值，经、纬向的剪切、弯曲、拉伸和压缩力学指标数据也均为取3块试样的平均值.

表2 实验结果Tab.2 Results of tests

2 数据处理与分析

2.1 拉伸弹性回复率与力学指标的回归分析

由纺织材料力学变形的基础理论可知，织物的拉伸弹性变形可能包含的基本变形形式有4种：拉伸、压缩、弯曲和剪切.因此，由KES系统测试的表2中的数据都可能与表征织物拉伸弹性回复性的拉伸弹性回复率有关.因此，借助Spss软件的回归分析方法，研究力学指标与拉伸弹性回复率的回归方程.回归方程分析的自变量为表2中所讨论的所有力学量.因变量为定力拉伸弹性回复率D1和织物经过10次定循环拉伸的定力弹性回复率D10.在置信度区间95%条件下，建立的多元回归方程如下：

由式（2）和式（3）看出，织物的定力拉伸弹性回复率和定力反复拉伸弹性回复率均可由各力学性能指标的回归方程计算得到，且表2中的所有力学性能指标都进入了回归方程，说明织物拉伸、压缩、弯曲和剪切性能的所有力学性能指标均与织物拉伸弹性回复性有关.

2.2 弹性回复率与力学指标的相关性分析

为了深入探究织物拉伸弹性回复变形的实质，并找出对拉伸弹性回复率影响较大的力学性能指标，以便改善织物的拉伸弹性回复性，本文分析了织物拉伸弹性回复率与其力学性能指标的相关性.

通过数据分析得到的织物各力学性能指标与拉伸弹性回复率的相关性由高到低如下（其中数字表示相关性系数）：

定力拉伸弹性回复率：

定力反复拉伸弹性回复率：

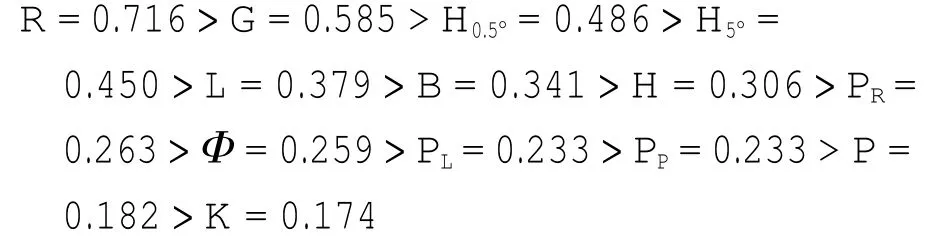
由以上织物各力学性能指标与定力拉伸弹性回复率和定力反复拉伸弹性回复率的相关性分析可以看出：①拉伸功回复率R和剪切刚度G对织物的定力拉伸弹性回复率和定力反复拉伸弹性回复率的影响较大；②剪切角为0.5°时的剪切力滞后量H0.5°、剪切角为5°时的剪切力滞后量H5°、拉伸线性度L对织物定力拉伸弹性回复率和定力反复拉伸弹性回复率的影响次之；③残余弯曲曲率K对定力拉伸弹性回复率的影响较大而对定力反复拉伸弹性回复率的影响最小；④压缩线性度PL和拉伸比功P对织物的定力拉伸弹性回复率和定力反复拉伸弹性回复率的影响均较小.

总结以上几点可以看出，提高织物的拉伸弹性回复性可以从改善织物的拉伸和剪切性能入手，提高织物的剪切刚度及织物的拉伸功回复率有利于改善织物的拉伸弹性回复率和反复拉伸弹性回复率.

3 结论

（1）本文通过试验及数据分析，分别建立了采用织物力学性能指标表示织物定力拉伸弹性回复率和定力反复拉伸弹性回复率的回归方程，且该回归方程的计算值与拉伸弹性回复率的实测值差异非常小，具有极大的实用性.

（2）通过分析织物拉伸弹性回复率与其力学性能参数的相关性，发现拉伸功回复率R、剪切刚度G对织物的拉伸弹性回复性影响最大，可以通过提高织物的剪切刚度及织物的拉伸功回复率来改善织物的拉伸弹性回复率和反复拉伸弹性回复率.

（3）本文所提出的2个织物力学性能指标，残余弯曲曲率K和残余剪切变形Φ，对织物拉伸弹性回复性有一定的影响作用，特别是残余弯曲曲率K对定力拉伸弹性回复率的影响较大，在精确表征织物拉伸弹性回复率的回归方程中是不可忽略的.

[1]赵立环，王府梅.服装廓形至关重要的织物弧度塑形性的研究：评价方法与设计要领[J].东华大学学报：自然科学版，2011，37（1）：28-34.

[2]秦丽，赵立环，王府梅.PTT织物记忆效果测试方法[J].纺织学报，2009，30（6）：39-43.

[3] ZHAO Lihuan，WANG Fumei.Evaluation methods forfabricwave plasticity[J].Tekstil Ve Konfeksiyon，2012（1）：32-39.

[4] ZHAO Lihuan，WANG Fumei.A study on the mechanism of fabric"wave"plasticity[J].Tekstil Ve Konfeksiyon，2013（3）：241-246.

[5]秦丽，张丽艳，赵立环，等.结构参数对PTT织物易塑型性和易护理性的影响[J].丝绸，2009（4）：30-34.

[6]张晓婷，高卫东，卢雨正.织物折皱回复角与其物理力学性能的关系[J].纺织学报，2008，29（6）：29-38.

[7]张晓婷.织物折皱回复性能的研究[D].无锡：江南大学，2008：25-32.

[8]赵立环，张杰.织物折皱回复角与其力学性能指标间的关系[J].纺织学报，2013，34（10）：39-42.

[9]张金秋，成玲，李佩隆，谷茜.羊绒针织物风格评定指标的优化分析[J].天津工业大学学报，2012，31（5）：42-45.

Relationship between fabric′s elastic recovery percentage of elongation and its mechanical properties

ZHAO Li-huan，WANG Bing-bing
（Division of Textiles，Tianjin Polytechnic University，Tianjin 300387，China）

To explore a more accurate and easy method for testing and characterization fabric′s tensile elastic recovery performance,the bending,shear,tensile and compression properties of fabrics were tested by KES-FB-AUTOA system tester,and two new parameters,residual bending curvature and residual shear deformation,were introduced based on the original mechanical parameters of KES system tester.Through data analysis,regression equations by which tensile elastic recovery rate and repeated tensile elastic recovery rate were calculated using mechanical parameters were established,respectively.The relationship between tensile elastic recovery rate and repeated tensile elastic recovery rate and mechanical parameters were analyzed.The results indicated that thtensile elastic recovery rate can be calculated by the regression equations with mechanical parameters under the condition of 95%confidence interval；Tensile response rates and shear stiffness have the greatest impact on the elastic recovery percentage of elongation,and hence fabric′s tensile elastic recovery performance can be enhanced by improving its tensile response rates and shear stiffness.

fabric；tensile elastic recovery rate；mechanical property；regression equation；relationship

TS101.1

A

1671-024X（2014）05-0018-04

2013-07-07

国家青年科学基金项目（51203114/E031401）；天津市教委科研计划项目（20120320）

赵立环（1981—），女，博士，讲师.E-mail:zhaolihuan@tjpu.edu.cn