一个博弈游戏的思考
王彦飞
摘要:本文通过一个游戏,探讨在不同的主体与目标下,对结果的影响。通过分析我们得出对于不同的主体,不同的目标,即使同一矩阵我们的结果会有很大差异。所以,面对不同的主体,我们不能简单地作出结论,我们要尽可能的了解对方,得到更多的信息,以便我们做出正确的判断。
关键词:博弈论;博弈分析
1.博弈论发展综述
博弈论英文译为Game theory,中文译为游戏理论,我认为其思想是战略与战略层面的,是怎样实现自我目标的学科。
冯·诺伊曼和摩根斯坦于1944年发表的《博弈论和经济学行为》一书,通常被看做是博弈论的开始。纳什在1950年提出将博弈论扩展到非零和博弈。“纳什均衡”概念的提出和证明奠定了现代非协同博弈论的基础,纳什均衡已成为大多数经济分析的关键概念。50年代是合作博弈发展的繁荣时期,60年代泽尔腾将纳什均衡概念引入动态分析,提出“精炼纳什均衡”概念,后期,海萨尼把不完全信息引入博弈论。
80—90年代是博弈论的成熟时期,博弈论已经作为一种一般的分析方法逐渐走进政治学,军事学,生物学,统计学,信息学等多门学科。
从1994年诺贝尔经济学奖授予了3位博弈论专家开始,共有6届的诺贝尔经济学奖与博弈论研究有关。可以看出博弈论再近几十年发展迅速,成果突出。
在一个博弈里主要有一下七个要素:游戏者,行动,信息,策略,收益,结果,均衡。
在博弈中,游戏者总是以利益或者效用极大化为自己的目标。
2.一个简单的博弈游戏
我们做一个简单的分析:
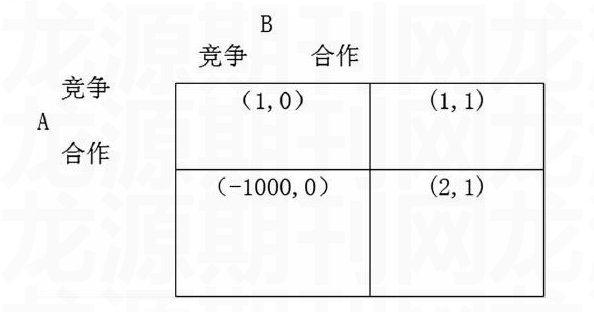
若A选择竞争,B选择竞争,结果是(1,0),B选择合作的结果是(1,1),所以此时B的收益为1(1>0),所以此时B会选择合作。若A选择合作,B选择竞争收益为0,B选择合作收益为1,所以B会选择合作。不管A怎么选B都是选择合作,合作是B的最优策略。
同样我们可以由B开始分析,若B选择竞争,A最好选择竞争(1>-1000),若B选择合作,A最好选择合作(2>1),所以B一定选择合作,而A知道B选择合作,则会选择合作,此时,均衡的结果是A合作,B合作,A收益为2,B收益为1。
以上结果是我们从博弈矩阵中得出的,仅是客观的,局外人来分析的均衡结果,但是如果我们是局内人,真的会有这么简单吗?
3.几个简单的假设
假设1:A与B是市场饿两家竞争垄断寡头,而且是仅有的生产同种商品的两家企业。
现在我们分析一下,会不会是(2,1)的结果。首先我们看A,A选择竞争,不管B是竞争还是合作,A的收益总是1。而若A选择合作,那么,若B选择竞争,结果是A得到-1000,B选择合作,A得到2,此时A的收益是不确定的收益,而且收益差异很大,虽然2选择合作是占优策略,但是如果B选择竞争,A选择合作,本来A想得到2,但是此时结果为(-1000,0)那么A的损失实在太大。
我们来看看B这样的威胁是否可信,总体上看B选择竞争与合作的收益总是0和1。两种结果(1,0)(2,1)两种结果都是B少收益1。(1,1)A,B收益相同,(-1000,0)中B的冒险选择竞争,所以这种威胁是可信的。
所以A的选择就会是竞争,此时如果B选竞争(想要打击A时)此时的结果是(1,0)A得1,B得0。此时与(2,1)结果中,A得2,B得1相比,B同样比A少1,所以(1,0)(2,1)结果是无差异的,但都是有利于A的;如果B选择合作,结果是(1,1),此时A,B两者收益相同,虽然相比(1,0)和(2,1),A的收益相对于B的优势减小,但是起码A与B的收益一样好。经过分析,A最好选择竞争。
此时我们再来分析B。如果B以同样的方式分析出A选择竞争,那么B最好是选择合作因为1比0好。接下来如果A也分析出B会选择合作,那么A的最好策略就是选择合作。但是此时的风险会太大,所以A依旧会选择竞争。
最后最有可能的结果就是(1,1)。当然如果B抱着打击A的心态选择策略的话,结果可能会是(1,0)。
假设2:A,B是两家完全竞争市场上的企业,生产同种商品。
同样,A看到B选择竞争时,对A的危害太大,所以A会选择竞争,B会选择什么呢?如果B确定A选择竞争,此时B应该会选择合作。但是如果B由此想,如果A推测B选择合作,那么A会选择合作,此时结果是(2,1),A得到的收益大于B的收益;那么B不如直接选择竞争,这既给A带来无威胁,同时收益又不为负,如果A选择合作,那么A很可能被淘汰出局,A选择竞争,结果是(1,0),和(2,1)相比,A的收益依旧比B的收益多,而且B没有更多的损失。在完全竞争的市场中,厂商多一个少一个对其他厂商几乎是没有影响的,所以B要干掉A,对B以后的发展及市场并没有太大的帮助,所以B最好选择合作,此时的结果是(1,1),A,B都得1的收益。
假设3:A,B是合作企业,是合谋者。
此时结果很明显。A,B同时选择竞争1+0=1;A竞争,B合作1+1=2;A合作,B竞争-1000+0=-1000;A,B都选择合作2+1=3。可以看出A,B都选择合作收益是最大的,当然得到的最大收益后,两家厂家可以协商进行收益的再分配。
当然我们可以做出其他假设,分析的过程可能存在很大差别。
4.结束语
可以看出,由于主体的不同和目标的不同,做出的策略有很大差别。策略的做出,首先要明确的是,我们的目标是什么,还有就是搞清楚大环境以及对手的情况,尽可能的手机对方各方面的信息。知己知彼,方能百戰不殆,信息越多,越能更好的分析出对手的优势和劣势,做出有利于自己的判断。同时在博弈中要注意对方的威胁是否可信。
笔者认为最困难的问题应该是博弈矩阵的确定。因为对信息的不充分问题,所以双方对对方的分析和自身的实际情况有很大不同,这会导致双方的博弈矩阵有所差别。这样就会使博弈双方在不同的矩阵中进行博弈。所以笔者认为,在未来,信息及数据的收集处理会至关重要。同样这也会使我们的生活产生巨大的变革。
博弈论是一门快速发展的学科,在它的发展过程中,会越来越多的应用到越来越广泛的领域,必将对各学科的发展起到巨大的推动作用。(作者单位:兰州商学院经济学院)
参考文献:
[1]李凌,王翔.论博弈论中的策略思维[J].上海经济研究,2010(1):35-41.
[2] 王文宾.演化博弈论研究的现状与展望[J].知识丛林,2009(3):158-161.
[3][以]罗伯特·j.奥曼.博弈论的目标[J].经济社会体制比较(双月刊),2006(4):1-22.

