气体管道路径自动寻优*

周 军 宫 敬 李晓平

(中国石油大学油气管道输送安全国家工程实验室)

近十年间，虽然全球经济低迷，但为满足人们的能源需求，全球的油气管道设计与建设仍然持续增长，2013年全球计划和在建管道有188 108km， 2011～2015年间计划与建设管道中75%为气体管道[1]。气体管道施工首先需确定管道路径，对于管道工程师已经是一项经常性和长期性的工作，并已做了大量尝试，传统上是在打印的地图上采用人工方式或优化理论进行求解，早在1971年Shamir U采用动态规划的方法确定手工网格上的管道最优路径[2]，2004年Hilde M和Joakim H、2012年 Marcoulaki E C等分别针对海底管道路径和地面管道路径优化问题，建立了考虑管道投资最少的数学优化模型，并采用模拟退火算法求解[3,4]。

路径选择需考虑管道的设计、建造、运行及维护等多种情况，如：管道的安全性、水力和热力条件、环境保护、历史遗迹、土木工程与水文条件以及建造要求等，目前基于智能算法的路径寻优，虽具有较好的全局性，但在考虑多因素和复杂环境约束条件下，目标函数的构建因人而异，且约束往往难于处理，此外，对于大规模网格下的路径优化问题，智能优化算法求解速度较慢，比如随着网格数目的增加，遗传算法中的染色体长度变长，计算时间显著增加[5]。笔者采用一种综合性的路径寻优算法，可简单、快速地确定管道路径。

油气管道路径规划问题的处理主要包括：油气产出、物性；管道起/终点，管道进/出口压力；管道通过的区域，区域高程，土地类型(岩石地，沙土等)；森林覆盖区、水源、河流、道路及铁路等不可穿越区；管道建设的材料、人工等费用，管径管材；地区法规；建设技术、建设目标(一般的投资费用最省)；其他影响管道建设的因素。笔者重点考虑环境因素，包括平面、起伏地形(高程)，不可穿越区以及不同的地表类型(岩石、河流、湿地等)等，采用数字化的地形数据，确定最优路径。

1 地形数据

路径寻优是在数字地图上进行的，连续的表用离散的数据替代，离散数据是连续地面起伏的近似表示，离散数据地图的分辨率越高，与真实地形越接近，优化的路径结果越准确，但是存在一个最高分辨率的限制，该格式与GIS(Geographic Information System)的栅格数据一致，具有良好的兼容性，称之为数字地图，取样地形如图1所示。

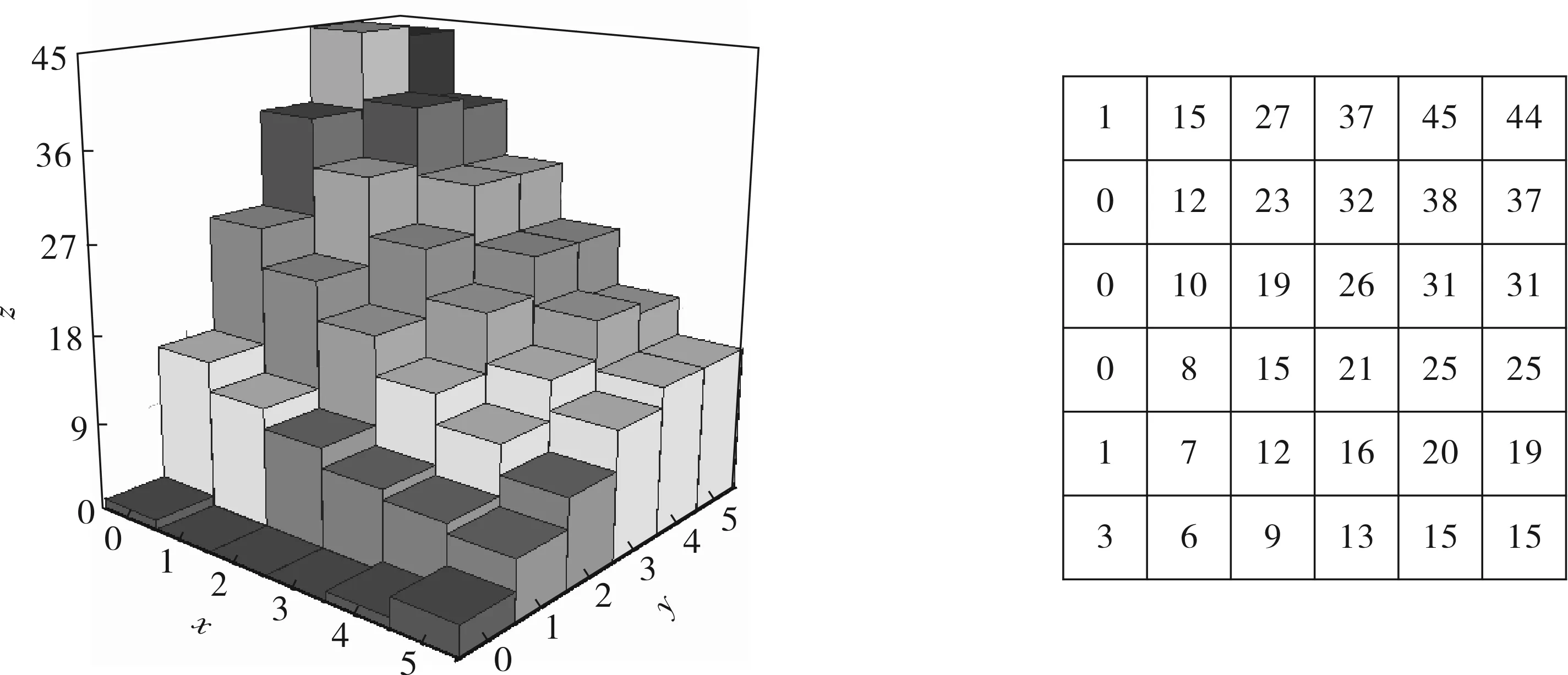
图1 取样地形(近似表示真实地形)

2 算法

最早、最著名的处理最短路径问题的算法是Dijkstra算法，该方法从起点开始逐步搜索并评估大量节点，计算并累加各节点的费用直至终点。由于此算法的搜索方向没有限制，对于大规模问题，计算时间很长。A*算法改进了Dijkstra算法，应用启发式的方式，在搜索过程中指导前进方向，减少了需评估节点的数量，降低了计算时间[6]。

2.1 邻接节点

从起点到终点选择一条路径，必须明确沿线节点搜索的选择方式，即从起点到终点确定最优路径中需评估的候选节点。在现实世界里人们决策时可向任意方向迈出一步，但是在数字地图上需要定义节点的邻接节点，一般包括3种方式：4邻接节点、8邻接节点和16邻接节点，图2中正中间的圆点定义为当前节点，其余各圆点为当前节点的邻接节点。

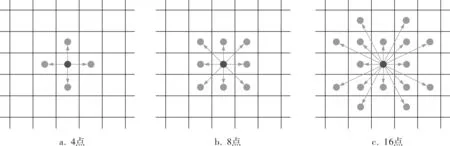
图2 邻接节点方式

2.2 费用与启发式函数

路径寻优的目的是确定费用最少的路径，这里的费用不仅是投资费用，它是更广义的费用，一般包括距离、投资、上升段长度以及管道积液量等。为了减少搜索区域，A*算法使用启发函数来指导搜索方向，比如搜索得到如图2b中正中间的圆点为当前节点，与此点邻接的有16个节点可作为下一个节点。对于这16个节点来说，总费用函数表示为：

f=g+h

(1)

式中f——起点到终点路径的总费用；

g——起点到当前节点的邻接节点实际累积费用，对于起点g=0，邻接节点的费用g等于起点到当前节点费用gc加上当前节点与邻接节点间的费用gn；

h——邻接节点到终点的评估费用，通常的评估函数包括曼哈顿距离函数、对角线距离函数和欧几里德距离函数3种[7]，笔者采用对角线距离函数。

算法(图3)通过评估邻接16个节点的总费用，取总费用最小的节点作为搜索的最优节点。该算法的主要部分包括OPENLIST和CLOSELIST两个列表，OPENLIST中容纳未访问的节点，CLOSELIST容纳已访问的节点，算法从OPENLIST取点加入CLOSELIST中直至找到终点。

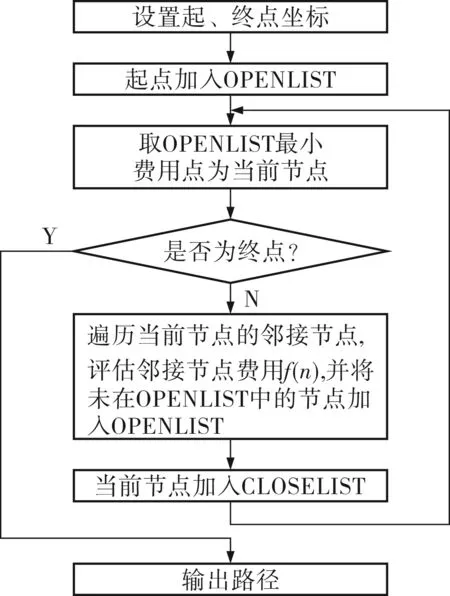
图3 程序框图

3 结果分析

使用地形模型函数生成数字地图，地形模型函数为：

(2)

地形模型函数的参数取值见表1。

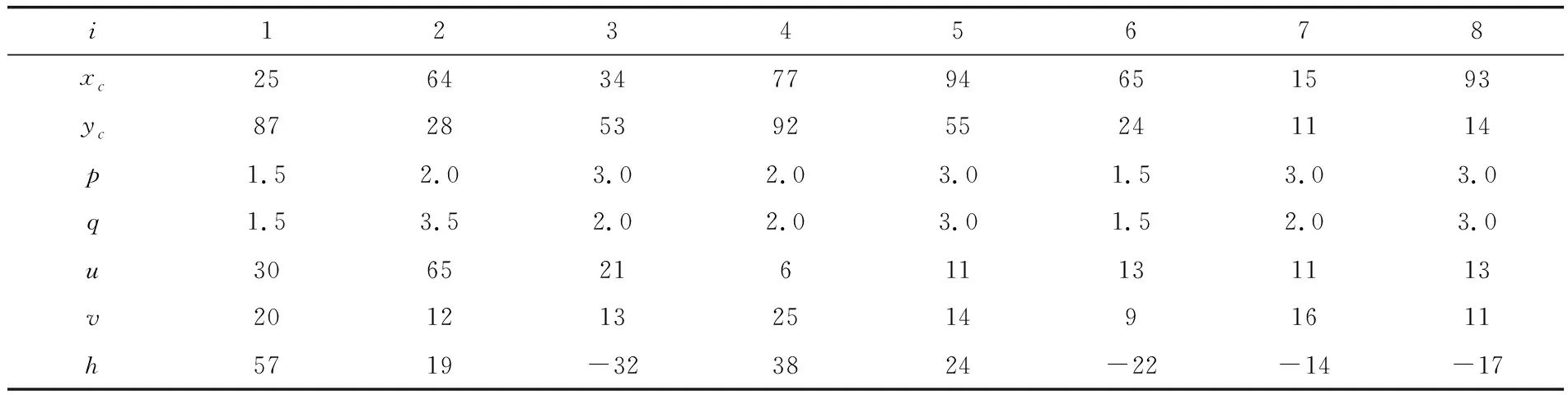
表1 地形模型函数的参数值

在此部分将介绍在模拟的栅格数据上不同条件下的路径规划，示例的数字地图如图4所示，网格数为20×20。

3.1 地形起伏下的最短路径

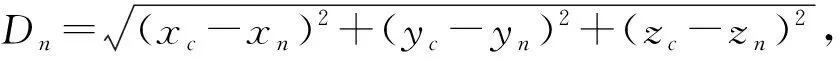
对于气体单相管流，管线压力损失主要来源于摩擦阻力，起伏地形下的最短路径即管道的最优路径，无需考虑水力约束。采用路径寻优程序可自动确定如图5所示起伏地形下的最短路径，从图5中还可以看出直线绕过低洼地区。

图5 起伏地形下的最短路径

3.2 避开障碍区的最短路径

如果在管道通过地区存在村庄、名胜古迹等不可通过区，管道需绕行，当此障碍信息输入计算程序后，可自动确定最优避障路径，如图6所示。

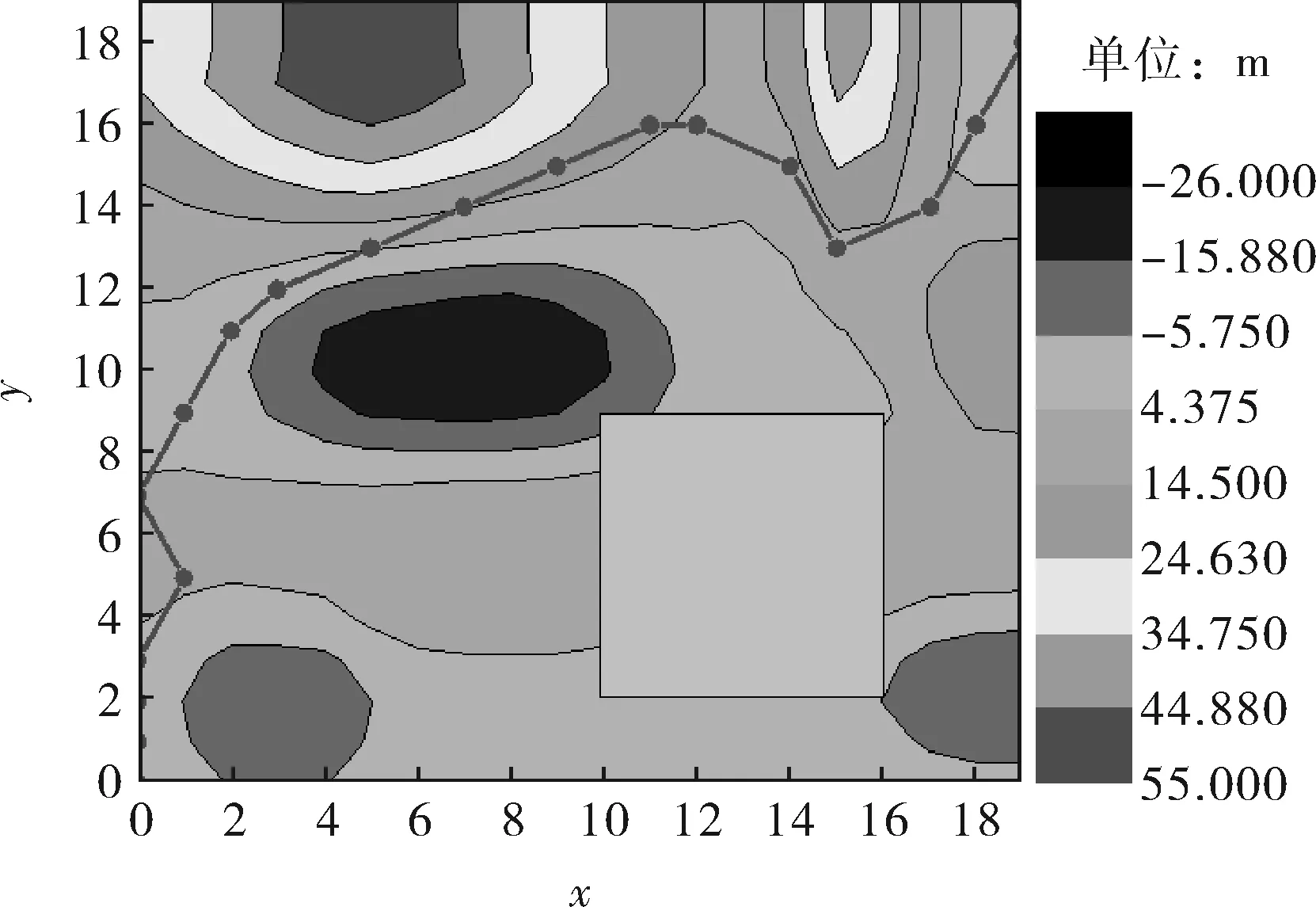
图6 避开障碍区的最短路径

3.3 地面类型

在管道铺设区域包括岩石、草地、沙土及河流等，称为不同的地面类型，管道经过这些地区时费用会有很大的差异，比如管道穿越河流时单位长度的费用远高于其他区域类型时的费用，该问题可描述为不同的区域类型下当前节点与邻接节点的费用gn不同。

笔者以含河流区域的管线最优路径为例，设非河流区域gn=Dn，河流区域gn=αDn，α为费用系数(根据管线穿越河流的具体情况而定)。

为了更好地说明此问题，另采用平面下不同类型图(图7)。图中深色为河流区域，白色为非河流区，设置20×20网格，网格大小1×1，设起点A(16，2)，终点B(16，17)，α=4。若管线采用直线穿越(虚线AB)，费用f=23.000，采用文中所示算法算得AB间路径的费用f=20.935，降低8.98%，穿越河流的费用系数越大，降低比例越大。同理，设置另一起点C(0，8)和终点D(19，19)，优化路径如图7所示，明显可看出，路径CD在河流最窄处进行穿越，可降低管线穿越费用。对于起伏地形和其他因素条件下的不同地面类型地图，该方法也可兼容。

对于复杂条件下的河流穿越问题，穿越河流有多种方式(开挖方式、气举沉管法、顶管和定向钻机穿越)，不同方式所用费用不同，管线穿越最终位置的确定应综合考虑水流、岸坡等因素，且应满足计算管线设计载荷[8]。该设计方法为工程设计人员提供了可供参考的路线设计方案。

图7 不同地面区域类型下的路径

4 结束语

笔者考虑各类环境因素，包括平面，起伏地形，不可穿越区，不同的地表类型(岩石、河流、湿地)等因素，使用数字化的地形数据，采用A*算法可自动确定气体管道最优路径。文中提到的管道路径设计框架，可根据工程实际费用进行扩充，为工程设计人员提供参考方案。油气管道路径寻优，管道管流包括单相和多相管道，多相管流不同于单相管流，对于一个起、终点高程相等的管线，如果是单相管流，上坡段损失的压力将在重力作用下在下坡段重新获得，因此管线压力损失来源于管道摩擦损耗，其仅是管道长度的函数而无需考虑沿线高程；在多相管流中，管线压降与沿线高程紧密相关，上坡与下坡段都是耗能过程，上坡段的能量损耗无法由下坡段重力补充，因此相同的起、终点位置和管线长度，不同的路径，沿线地形起伏不同管线具有不同的水力学特性。笔者只讨论了气体管道，重点论述多种环境因素的综合性路径优化方法，对于多相流管段具有兼容性。对于多相流管道，路径设计除考虑笔者提到因素，还需重视管道的水力特性，将路径寻优与水力条件结合。

[1] Tubb R.Pipeline & Gas Journal’s 2013 International Pipeline Construction Report[R]. Pipeline Gas Journal，2013.

[2] Shamir U.Optimal Route for Pipelines in Two-phase Flow[J].Society of Petroleum Engineers Journal，1971，11(3)：215～222.

[3] Hilde M，Joakim H，Gudmund O.Optimization of Pipeline Routes[C].The Fourteenth International Offshore and Polar Engineering Conference，France：2004: 50～55.

[4] Marcoulaki E C，Papazoglou L A，Pixopoulou N.Integrated Framework for the Design of Pipeline Systems Using Stochastic Optimisation and GIS Tools[J].Chemical Engineering Research and Design，2012，90(12)：2209～2222.

[5] 杨大地，冉戎.基于遗传算法的曲面最短路径求解[J].计算机仿真，2006，23(8)：168～169.

[6] Russell S，Norvig P.Artificial Intelligence: A Modern Approach[M].English：Prentice Hall，1995：97～101.

[7] Wichmann D R.Automated Route Finding on Digital Terrain[D].New Zealand：University of Auckland，2004.

[8] 王桂龙，黄红毅，陈遥，等.燃气管道穿越河流工程的设计[J].煤气与热力，2002，22(3)：266～268.