碳的雨贡纽状态方程及动压合成金刚石机理①——动压合成金刚石之二

张书达

（天津市乾宇超硬科技有限公司，天津 300384）

1 碳的雨贡纽状态方程

冲击波到达前方的固体后会在固体中传播，这时固体被强烈地压缩。冲击波越强，固体所受的压力越大，因而密度提高得也越多。冲击波压缩固体的过程必须遵守质量守恒、动量守恒和能量守恒三个定律以及固体状态方程。对于定常击波，服从多方过程规律pυk＝常数的完全气体，则有

式中：E——内能，υ——比容，ρ——介质密度，k——介质的等熵指数，υ＝1／ρ，p——介质压力。脚码1、2分别代表推动前和推动后。

上述关系式称为雨贡纽（Hugoniot）状态方程。这些守恒定律和关系在压力－比容平面上确定了一条曲线pH（υ）。这就是冲击压缩雨贡纽曲线（shock compression Hugoniot curve）。它代表了固体被不同强度的冲击波压缩后所达到的状态。有的文献亦称之为兰金－雨果扭曲线（Rankine－Hugoniot curve）或称为冲击绝热线、Hugoniot（雨贡纽）绝热线。

根据热力学第二定律，绝热的无限缓慢的压缩过程可以认为是等熵压缩。在等熵压缩过程中，系统的态函数——熵恒定，即ds＝0。

雨贡纽冲击绝热曲线或Hugoniot（雨贡纽）绝热线，表示适合于多方介质中冲击波的能量守恒定律。图1为雨贡纽冲击绝热曲线（Hugoniot线）的示意图。

图中点A（p1，υ1）——介质未扰动状态；点B（p2，υ2）——冲击波压缩后介质状态。显然，（p2－p1）／（υ1－υ2）＝tgα，α——直线AB与横坐标倾角，它决定了物理量D和u。D——爆速，等于化学反应区的移动速度，u——粒子速度。

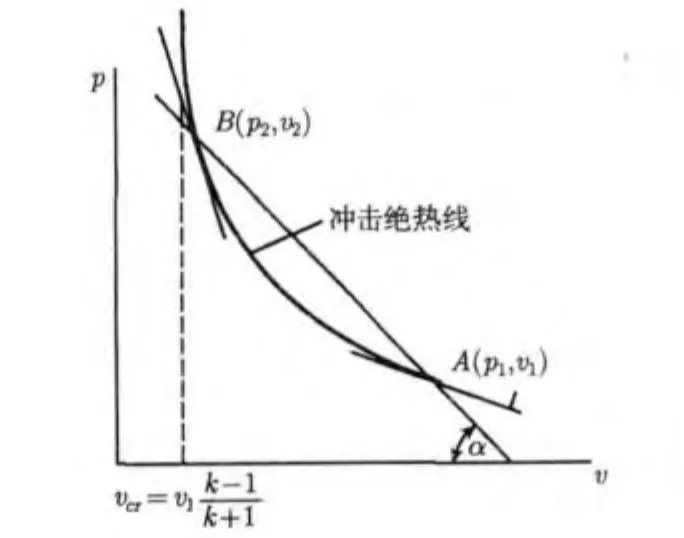
图1 雨贡纽冲击绝热曲线（Hugoniot线）Fig.1 Hugoniot impact adiabatic curve

诸多研究人员针对不同情况提出了多种雨贡纽冲击绝热曲线（Hugoniot线）的计算方法及计算结果［1～8］。

在研究动压时，常提到CJ面，即查普曼－儒盖面（D.L.Chapman－E.Jouguet）。它是指定常爆轰中区分化学反应区和爆轰产物的界面（图2中的H－H面）。

CJ面处爆轰产物的参数称为爆轰波参数或查普曼－儒盖（CJ）参数。原始炸药与化学反应区的分界面是冲击波阵面（图2中的B－B面）。所有查普曼－儒盖参数都以下标“H”的形式标出。

图2 爆轰波的基本关系Fig.2 The basic relationship between the detonation wave

D——爆速，等于化学反应区的移动速度；uH——波阵面后爆轰产物的速度；pH，ρH，TH——化学反应区后爆轰产物的状态参数；p0，ρ0，T0——化学反应区前原始炸药的状态参数。爆轰过程是定常的，即D＝常数。

Hugoniot绝热方程可写成下式：

式中：EH、E0分别是CJ面处爆炸产物和原始炸药的总比内能，2式中总比内能中包含了生成焓。众所周知，根据热力学的函数关系，总焓

将（3）代入（2）即可得出

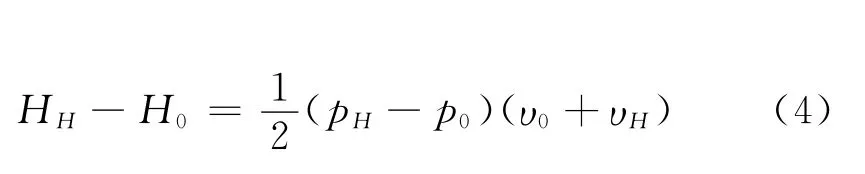
公式（4）更适用，因热力学手册通常给出理想状态下总焓值。

为计算动压中的参数，我们可以列出如下联立方程组

该方程组为5个未知数的四个方程联立组，只要给定冲击波的任一参数值，就可确定其余各参数值。

具体到金刚石和石墨，邵丙璜介绍了ПавловскийМ.Н.［9］和 Alder B.J.［10］的工作，雨贡纽方程可以简化成下式［11］：

其中A，n是常数，金刚石的A＝217.0GPa，n＝2.5；石墨的A＝52.7GPa，n＝1.22。用上式描述冲击绝热（雨贡纽）曲线误差不大（≤2%）。图3和图4分别示出了金刚石和石墨的雨贡纽曲线。

图3 金刚石的雨贡纽曲线Fig.3 Diamond Hugoniot curve

图4 石墨的雨贡纽曲线Fig.4 Graphite Hugoniot curve

Fried和 Howard［12］对碳的4种相态——石墨、金刚石、类石墨液碳（液相1）、类金刚石液碳（液相2）作了详细的研究，对碳的4种相的Gibbs自由能给出了精确的数值计算公式。碳的4种相的Gibbs自由能的具体计算公式适用范围：O≤p≤600GPa，300K≤T≤15000K。

李德华［13］通过计算认为，以下炸药爆轰产物CJ点的游离碳更可能存在的相分别为：

PETN（C5H8N4O12，ρ0＝1.77g／cm3）——类石墨液碳，

RDX（C3H6N6O6，ρ0＝1.80g／cm3）——类金刚石液碳，

HMX（C4H8N8O8，ρ0＝1.90g／cm3）——金刚石，

TNT（C7H5N3O6，ρ0＝1.64g／cm3）——类金刚石液碳，

TATB（C6H6N606，ρ0＝1.895g／cm3）——类石墨液碳，

Cyclotol（C5.045H7.461N6.876O7.753，ρ0＝1.743g／cm3）——类石墨液碳等。

对于炸药爆轰产物中的单组分的Hugoniot曲线，有详细的实验测量结果。实验结果可参考相关文献资料，如石墨和金刚石［14，15］等。

2 动压合成金刚石原理

2.1 相图

众所周知，在常压下金刚石是处于亚稳态而石墨是处于稳定态的；在高压下正好相反，金刚石处于稳定态，而石墨处于亚稳态。图5给出了碳的高压相图，不同的实验给出的数据是有差异的，但总的趋势是大体一致的。欲使石墨转变成金刚石，需要利用动压创造高温高压的条件。图（a）中给出了据BKW物态方程（Becker－Kistiakowsky－Wilson爆轰产物状态方程）计算的各种炸药爆轰产物在CJ面上的参数［16～18］；图（b）给出了不同合成方法在相图中的区间［19］。

金刚石与石墨的相平衡线可用Berman和Simon给出的下式估算［20］

而Strong和Haneman给出的计算公式如下［21］

杨向东等人［22］研究了高温高压下三相碳（石墨、金刚石、液相碳）的状态方程，包括高压下石墨到金刚石的固－固相变以及高温下石墨和金刚石的熔解曲线。计算所得到的金刚石熔解曲线具有正的斜率，石墨－金刚石－液相三相点为4400K、14GPa左右。

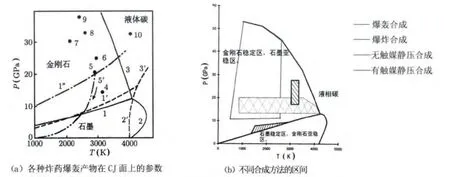
图5 碳的高压相态图Fig.5 High－pressure phase diagram of carbon

2.2 爆轰法

在密闭的爆炸罐中引爆炸药，利用负氧平衡的状态，使炸药爆轰产物中的部分固态碳在瞬间的超高压超高温下转变成金刚石。当然，爆轰波中的压力应符合金刚石的热力学稳定区条件（p≥10GPa）；而爆轰波形成的高温（T≥2000K）又可加速相变的进程。由于符合这一条件的时间很短，约为微秒级，故金刚石颗粒的粒径绝大部分处于10nm以细的范围。但由于二次团聚会形成20～100nm的颗粒。这就是爆轰纳米金刚石，可以说是没有多晶的纳米金刚石。

选择不同的炸药组合和不同的爆轰条件，纳米金刚石的产量和粒度会有不同。斯塔纽科维奇（СтанюковичК.П.）早期的工作比较系统［23］，表1列出了这些数据对比，现在仍有参考价值。试验是在2m3充以惰性气体的爆炸室中进行的。

表1 爆轰合成纳米金刚石的数据Table 1 Data of nanodiamond synthesis by detonation method

文潮等人［24］独辟蹊径，研发了用炸药爆轰法制备纳米石墨粉的方法。石墨结构的平均晶粒径为1.86nm～2.58nm，颗粒呈球形或椭球形。纳米石墨或许在不远的将来会开发出广泛的用途。

2.3 爆炸法

利用炸药的冲击波作用于石墨可以制造多晶纳米金刚石。它的晶粒是纳米级，在冲击波的强力压缩下形成聚晶体［25］。后者可以达到几微米甚至几十微米。为了确保石墨转化成金刚石的速度是有意义的，一般需要使压力达到10GPa和温度达到2000K。

邵丙煌等人用爆炸法做了制造多晶纳米金刚石的实验［26］。在强激波作用下，石墨转变为金刚石的显微结构表明，形成的金刚石是聚晶体，大小在1～5μm之间，和原始的石墨晶粒相当。聚晶体本身由两种晶格模型的单晶金刚石所组成，单晶体的大小在1～4nm和10～160nm之间。由这些聚晶体再进一步聚集，形成粒度小于36μm的金刚石微粉。这与静压法形成的金刚石的结晶形态不相同。他们还对爆炸作用下石墨转变为金刚石的机理和有关的力学参数进行了理论分析和计算。爆炸法人造金刚石与罕见的天然聚晶金刚石相似，各向同性，无解理面。由于聚晶结构使每个颗粒都具有大量微观切削点。因此在研磨和抛光宝石、瓷器、铁氧体等材料时，其速率和精度高于单晶的天然或人造金刚石。

为尽量减少金刚石向石墨的逆转变，加入大量的导热物质是有益的。波留米尔使用铜粉－石墨粉混合（92%铜，8%石墨），并采用大质量炸药（～1000kg），金刚石产出可达石墨质量的80%，金刚石尺寸1～100μm［27］。类似方法可合成cBN。

图6示出了爆炸法制金刚石相变过程在相图中的位置变化［28］。

图6 冲击引起石墨→金刚石相转变进行过程示意图Fig.6 Schematic diagram of phase transition process from graphite to diamond caused by impact

张万甲［28］对相变机理做了比较详细的研究。当冲击波达到稳定的峰值压力时，形成热斑的机制消失。热斑与周围介质达到热平衡。这相当于图6中的A→B过程，B态相应于波后状态。在稳定的B态，虽然还存在原子的热扩散，但热扩散速率很低，所以在冲击波阵面后，不管峰值压力的持续时间有多长，对金刚石的产出率都不会产生明显的影响。由此得出，热斑区在波阵面厚度的特征时间内，石墨发生了固－液－固或固－汽－液－固的顺序相变。即在冲击波阵面内完成了石墨→金刚石的相转变。由于相转变的特征时间很短（1μs左右），过冷度很大，在这种条件的制约下，使冲击合成金刚石微粉的粒度只能达到微米量级。图6中O－A－B阶段分别代表热斑区在波阵面厚度的特征时间内发生石墨→金刚石的转变过程。B－C－O阶段分别代表在波阵面后整个样品系统的稀疏膨胀和冷却过程。在这个阶段中将发生金刚石→石墨的逆转变。O－A－BC－O一个周期便决定了每次冲击合成时，金刚石的数量和质量，同时也决定了其它形式的碳如碳黑等的出现。

张凯提出了爆炸相变的结构转变模型——“凯”模型［29］。在ABC型石墨中，找到了具体的18个碳原子向金刚石晶胞转变的原子对应点结构，使活化能接近最小值。在AB型石墨转化中，除石墨网格平面间的压缩外，必须考虑层间剪切错动的作用，二者的概率同样多。标志其特征错动的距离是0.521h，h——层间压缩距离。

爆炸法的另一个应用是用冲击波作用于铸铁。由于铸铁块中的温度压力达到金刚石的热力学稳定区，其中的部分石墨会转变成金刚石。铸铁的散热效果好，金刚石逆变成石墨的几率较小。这种方法生产的金刚石都是单晶，以微米级为主。

2.4 激光法

刘常龄等测量了激光维持爆轰波（LSD波）的压力，在3.9×1014W·m－2激光辐射能流率（即通常所说功率密度）时，靶面峰值压力为2.38GPa［30］。激光脉冲上升时间可以短到纳秒级，而曹启明做到1.67ns［32］，长春艾克思科技有限责任公司研制的180NP－2激光探测器其脉冲上升时间仅180ps。如按这2个上升时间计算，压力上升速率为（1.43～13.2）×106GPa·s－1，此数值可以达到远高于爆轰波的压力上升速率。王荣波等人［33］测试了爆压为10GPa的爆轰波，上升时间小于4ns，即该爆轰波的压力上升速率为2.5×106GPa·s－1。可见，激光爆轰波与炸药爆轰波的压力上升速率大体相当。尽管激光爆轰波的压力比炸药爆轰波低很多，但压力上升速率有时可以做到远高于后者，这无疑有利于激光诱导石墨向金刚石的相变。所以，激光法合成金刚石应该作为动压合成金刚石的方法之一。

早在1983年，Fedoseev［34］首先用此法合成了金刚石。对于它的成功，早已无疑问了。但对它的合成机理较全面研究的却甚少，许多学者都希望仅从热力学和／或晶体微观结构角度得到解释。张书达［35］系统地分析了激光诱导合成金刚石的机理，并进行了多方面的较深入的探索。将宏观的热力学理论与微观的物质结构及相变的微观机理结合起来，能较好地阐明该相变机理。下文略加介绍。

2.4.1 光压和激光脉冲冲击波压力

麦克斯韦从经典的电磁波理论出发，推导出光压计算公式：

式中：P光——光压，C——光速，E——每秒入射到单位面积上的能量，ρ——界面反射系数，对于绝对黑体ρ＝0，对于理想镜面ρ＝1。

设激光源的功率密度为3.9×1014W·m－2，对于石墨或碳黑，可以近似认为ρ＝0。于是用公式（3）计算的相应的P光＝1.29MPa。

因激光脉冲可产生冲击波压力，已属于非线性光学的范畴，激光束的辐射力非常强。

按More的研究，激光脉冲冲击波压力可用下式计算［36］：

式中：p激——激光脉冲产生的冲击波压力，I0——入射激光辐射能流率（功率密度），以1018W·m－2为单位，计算中认为激光吸收效率～60%。

若I0＝3.9×1014W·m－2，则用（4）式计算得p激＝1.37GPa。

在强激光作用下，靶蒸汽前沿成为高密度等离子体，形成超声速的激光维持爆轰波（LSD波），于是对靶面造成了相当大的冲量和压力。刘常龄等人测量了LSD波的压力。在3.9×1014W·m－2的激光辐射能流率下，LSD波的靶面峰值压力为2.38GPa［31］。这比用公式（4）计算之值要大73%。

较新的激光器的输出功率可高达1012W量级［32］，如聚焦于500μm×500μm的范围内，则它的激光辐射能流率高达1018W·m－2量级，相应的光压已达104GPa。这早已到达金刚石的热力学稳定区。

2.4.2 热压力

晶体的状态方程可以写成［37］：

式中：E——晶体热振动总能量，U——总相互作用能即结合能，υ——比容。右边第一项是与晶体势能有关的压力；第二项是与晶格热振动有关的压力，称为热压力。从上式可以看出，晶体热压力等于它单位体积热振动能量的γ倍。大多数晶体γ为1～3倍（格林乃森常数）。

在高温时，

式中：N——阿佛加德罗常数，K——玻尔兹曼常数，T——温度。

若T为2500K，γ取平均值2，则p热≈0.3GPa。

2.4.3 纳米固体颗粒的表面高压

具有弯曲表面的材料，其表面应力正比于其表面曲率。由于纳米粒子表面曲率非常大，所以其表面应力也非常大，使纳米颗粒受到高压压缩。如半径为10nm的水滴，其压力有14MPa［38］。若为球形且各向同性，则粒子内部受到的压力为：

式中：r——颗粒半径，σ——表面应力。该式也适用于任意形状的小面化晶粒。

根据 W.D.Harkins原理［39］，晶体在0K时的表面能，等于破坏单位面积内全部键能所需能量之半。对于ABC型石墨，其晶胞表面积为0.6756nm2。取1个晶胞表面会切断18个σ键和12个大π键。其平均键能为360kJ·mo1－1，则可计算出每个C健的平均键能为1.495×10－19J。于是用公式（7）可计算出石墨的表面能平均为σ＝3.319J·m－2。

设r＝10nm，则p粒＝0.6638GPa。现在用爆轰法制备的纳米石墨，其平均粒径约为4nm，即r＝2nm，则p粒＝3.32GPa。

从以上分析可知，所用石墨原料颗粒越细，则所受压力越高，越有利于向金刚石的相变发生。

2.4.4 相变条件与光化学

关于石墨转变成金刚石的相变条件，经典的理论是△G＜0的判定法，即只有当△G＜0时，才能使相变进行下去。式中G是系统的吉卜斯自由能或称自由焓。根据这一理论计算出了上述相变在298K时的临界压力应为1.49GPa［40］。也就是说，当系统压力低于这一数值时，石墨转变成金刚石的相变是不可能发生的。

近年来在多种常压或低压下制备金刚石方法研究成功，这使得上述理论遭遇困难。事实上△G判定理论是由热力学理论引进相变过程研究中的。形成于19世纪的热力学的方法是根据由经验总结得到的自然界的基本规律而作的演绎推论，它的理论具有高度的可靠性与普遍性。但它的最大缺点是忽视了物质的微观结构，因而有许多现象不能解释，例如统计涨落、隧道效应等。

从微观角度解释，石墨变成金刚石的本质是C原子的电子态由SP2杂化转变成SP3杂化。而这一转化不一定要高压。一些化学反应证明了这一点。例如：

众所周知，CCl4是四面体结构，其C原子的电子态即是SP3杂化。

由光引起的化学反应叫光化学反应。研究光化学反应的光化学是化学领域的重要分支之一。可见光是可能改变原子的电子态的，而激光的本领更大于普通强光。激光可引发催化、分子剪裁、提纯、Ph突变、同位素分离……

光化学反应的速度常数K与热化学反应一样，满足Arrhenius方程：

式中：A——常数，E0——反应活化能，R——气体常数。与热化学反应相比，光化学反应中E0较小，因而可在较低温度下获得较大K［41］。

从物理化学的研究可知，光能使某些自由焓增加的反自发过程得以实现。激光的应用更使光化学进入崭新的阶段。实际上激光诱导合成金刚石是固体相变与光化学的交叉学科。

4.4.5 势垒的估算

由石墨到金刚石的相变，必须越过某一势垒。这一势垒远大于石墨与金刚石的焓差。二者的焓差约13～15kJ·mol－1（不同文献数据有差异）。至今为止，尚未见到具体计算这一势垒的文献。本文则试图作一估算。

内能是原子（分子）无规则热运动的机械能的统计平均值。通过对石墨加温加压使其直接转变成金刚石。用系统内能的增加量作为必须越过的势垒的量度是较为科学的。根据热力学函数的关系：

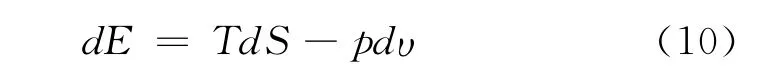
式中：E——内能，T——温度，υ——比容，p——压力。

根据文献［42］的数据，石墨的熵值为5.69（298.16K），11.65（600K）和28.45（1200K）J·mol－1·K－1等。作者利用此组数据总结出T与S有下述关系

此式的偏差约1%。

早在1963年，Bundy［16］就发表了他的直接转变结果：在12.5GPa和3000K的条件下，石墨在无触媒的参与下直接转变成金刚石。利用公式（11）可外推出3000K时石墨的熵值为58.35J·mol－1·K－1。于是：

Андреев通过金刚石晶体内的压缩石墨测量了石墨被压缩的效果：当内压为2.5GPa时，C轴的平面间距由dc＝0.337nm（常规，理论值为dc＝0.335nm）减小至dc＝0.320nm，而平面内无可测得出的变化［43］。据此，我们可以计算出石墨的压缩系数为2.018×10－11Pa－1。常态下石墨的比容：

在压力为12.5GPa时，其比容为3.952×10－6m3·mol－1。

由（10）（12）（13）可得：

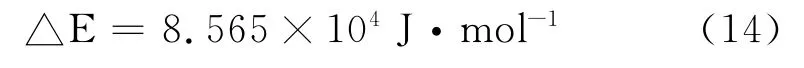
曾有人估算过由石墨形成金刚石晶核最少的碳原子数为98.1mol石墨的C原子数为6.022X 1023。于是，形成金刚石晶核需要越过的临界势垒为

作一粗略近似，如98个原子组成一个小立方体，可认为朝向激光束方向的晶面有21个碳原子。石墨层面内C－C键长为0.142nm，平均每个碳原子所占面积为2.6193×10－20m2。21个碳原子所占面积为5.50053×10－19m2。设激光束辐射能流率为1014W·m－2，则照射到相应于金刚石临界晶核的石墨层面上的能量为：

一般原子维持在激发态的时间为10－7～10－8S。上式计算中取了下限10－8S。

石墨可粗略认为接近绝对黑体。它对可见光的反射率和透射率都极小，这对它吸收激光能量是极为有利的。从上述计算可知，只要激光源的辐射能流率大于2.534×109W·m－2，即可能使98个碳原子越过势垒而形成金刚石晶核。上述计算数值与诸多所发表的工作是相符的。实际上，石墨吸收可见光能量高达90%以上。

据△E可计算出形成金刚石晶体时，平均每个石墨碳原子必须越过的势垒为1.422×10－19J。而波长为532nm的黄光中每个光子的能量为3.74×10－19J，只要一个碳原子吸收一个光子能量的38%，即可能由SP2态转变到SP3态。

碳的第一电离势为1.086×106J·mol－1［44］，此值远大于一个碳原子由SP2到SP3所需越过的势垒。所以，石墨在激光照射下转变成金刚石很可能是不经过等离子这一阶段的。这与某些工作者的分析是不同的。

2.4.6 表面原子振幅大

Prutton的研究表明，表面法线方向上原子振幅比体内的大很多。用FIM法观测到，单个原子有1eV数量级的（相当于1.602×10－19J）的动能［45］。

2.4.7 高温加大原子振幅

激光照射的高温效应是众所周知的。据德拜模型，高温时原子的均方位移（平均振幅）与温度T成正比［46］：

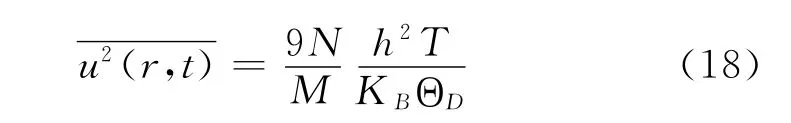
式中：M——晶体总质量，N——晶体中原子数目，KB——玻尔兹曼常数，h——普朗克常数，ΘD——德拜温度。

由公式（18）可见，2500K时的平均振幅是298K时的8.39倍。而强光照射到石墨表面达到2500K是不难办到的。

Pavlovska等人用实验证实了高温下晶体表面会粗糙化［47］，即证实了表面原子振幅加大。

2.4.8 石墨碳原子可连续吸收光子能量

通过研究晶格振动和晶体热容可知，在高温下量子效应可以忽略［48］。也就是说，在高温下石墨碳原子可连续吸收光子能量，从而有利于SP2向SP3转变。在连续吸收光子能量方面，可以把光看作经典光的条件是每立方波长的光子数必须远大于1。对于现代强激光场，这一数值高达1014，甚至更高［49］。

2.4.9 晶体结构转换机制

王金斌等人探讨了脉冲激光诱导液－固界面反应法（PLIIR：pulsed－laser induced liquid2solid interface reaction）制备金刚石纳米晶的物理化学机制，提出了金刚石纳米晶的成核机理，即由激光诱导石墨六方结构原子团过渡到石墨菱方结构、然后转变成立方金刚石晶核，以及由石墨六方结构直接转变成六方金刚石结构的相变模型，并讨论了基于液－固界面反应的纳米晶生长动力学，较好地从动力学上解释了PLIIR合成金刚石纳米晶的物理化学机制［50］。

［1］胡绍鸣，李辰芳.爆轰模型熵问题的探讨［J］.高压物理学报，2004，18（4）：345－352.

［2］李银成.爆轰产物物态方程（Ⅰ）——爆热、爆轰产物的等熵方程和物态方程［J］.高压物理学报，1998，12（4）：271－281.

［3］曾代朋，陈 军，谭多望.超压爆轰产物冲击绝热线的实验研究［J］.高压物理学报，2010，24（1）：76－80.

［4］杨向东，张宏，曾勇，等.石墨冲击压缩的理论研究［J］.高压物理学报，1997，11（1）：66－69.

［5］陈 军，曾代朋，谭多望，等.超压爆轰产物声速以及热力学CJ点的实验研究［J］.高压物理学报，2010，24（3）：201－205.

［6］曲志明，周心权，王晓丽，等.掘进巷道瓦斯爆炸冲击波状态参数的结构分析［J］.矿业安全与环保，2006，33（3）：1－6.

［7］安建军，张志杰，王文廉.利用冲击波速度间接测试超压值的可行性研究［J］.中国测试技术，2008，34（3）：131－134.

［8］丁广骧.煤矿巷道瓦斯爆轰理论分析和参数计算［J］.中国矿业大学学报，2000，29（1）：37－40.

［9］ПавловскийМ.Н.Физикатвёртоготела，1971，13（3）.

［10］Alder B.J.，Cristian R.M.Phsy.review letters，1961，7（10）.

［11］邵丙璜，汪金通.强击波作用下石墨转变金刚石的相变动力学［J］.物理，1979，8（3）：205－211.

［12］Fried L E.，Howard W.M.，Explicit gibbs free energy equation of state applled to the carbon phase diagram［J］.Phys.Rev.，2000，B 61（21）：8734－8743.

［13］李德华.炸药爆轰参数、生成热及爆热的理论研究［D］.成都：四川大学，2005.

［14］McQueen R.G.，Narsh S.P.，Behavior of Dense Nedia under High Dynamic Compression［M］.New York：Gordon and Bereaeh.1968.107

［15］Gust W.H.，Phys.Rev.，1980，B22：4744.

［16］Bundy F.P.，Direct conversion of graphite to diamond in static pressure apparatus［J］.J.Chem.Phys.1963，（38）：631～638.

［17］ГубинС.А.，ОдинцовВ.В.，ПепекинВ.И.，Оролифазового состояния углерота при оценке параметров детонации конденсированныхвеществ［J］.Хим.Физика.1984，3（5）：754～766.

［18］ГубинС.А.，ОдинцовВ.В.，ПепекинВ.И.，идр.Влияние формы и размера кристаллов графита и алмаза на вазовое равновесиёуглеродаипараметрыдетонации［J］.Хим.Физика.1990，9（3）：401～417.

［19］ГубаревичТатьянаМихайловна.私人通信，2001.

［20］R.Berman and F.Simon，Zeit fur Electrochemie［J］，1995，59：33.Ian L.Spain，Jac Paauwe.High Pressure Technology［M］.New York and Basel：Mzrcel Dekker，INC 1977，135.

［21］H.M.Strong，R.E.Hanneman，Crystallijation of Diamond and Graphite［J］.J Chem Phys，1967，46：3668～3676.

［22］杨向东，张宏，胡栋，等.高温高压下碳的状态方程及相变理论研究［J］.高压物理学报.1997，11（4）：250－253.

［23］СтанюковичК.П..Неустановившиесядвижениясплошной среды［M］.Москва：Наука，1971.855.

［24］文 潮，金志浩，关锦清，等.炸药爆轰法制备纳米石墨粉［J］.稀有金属材料与工程，2004，3（6）：628－631.

［25］勘探技术研究所.爆炸合成聚晶金刚石的试验［J］.人造金刚石，1977（3）：7－9.

［26］邵丙璜，周之洪，汪金通，等.爆炸法人造金刚石［J］.爆炸与冲击，1986，6（3）：198－207.

［27］ПрюмерР..Абработкапорошкообразныхматериаловвзрывом［M］.Москва：Мир，1990.200.

［28］张万甲.冲击引起石墨→金刚石相转变机理的探讨［J］.高压物理学报，2004，18（3）：209－219.

［29］张 凯，张路青.石墨通过爆炸相变为金刚石的新结构位置转变模型［J］.超硬材料工程，2013，25（2）：26－30.

［30］刘常龄，王春彦，袁永华，等.激光维持爆轰波的冲量和压力［J］.高压物理学报，1993，增刊：70

［31］钟锡华.现代光学基础（第二版）［M］.北京：北京大学出版社，2012，206.

［32］曹启明.基于可调纳秒脉冲LD的激光引信接收机测试光源系统研究［D］.天津：天津大学，2010.

［33］王荣波，田建华，李泽仁，等.GI－920炸药爆轰波阵面的光纤探针测量［J］.火炸药学报，2006，29（2）：7－9，14.

［34］D.V.Fedoseev，V.L＿Bukhovets，I.G.Varshvskaya，et a1［J］.Carbon，1983，21：237－241.

［35］张书达，孙 景，翟 琪.激光诱导合成金刚石的机理研究［J］.金刚石与磨料磨具工程，2005（6）：1－5.

［36］Richard M.More［J］.Laser Interaction and Related Physical Phenomena，1981，5：235.

［37］苟清泉，固体物理学简明教程［M］，北京：人民教育出版社，1979，85～86.

［38］姚寿山 李戈扬 胡文彬，等.表面科学与技术［M］.北京：机械工业出版社，2005，30.

［39］W.D.Harkins Energy Relations of the Surface of Sosids［J］.J Chem Phys，1942，10：268～272.

［40］王文清，等.物理化学习题解答［M］.北京：北京大学出版社，1991上册146.

［41］张永康.激光加工技术［M］.北京：化学工业出版社，2004，152.

［42］王光祖.人造金刚石探密 ［M］.杭州：浙江大学出版社，2001，44.

［43］В.Д.Андреевидр.［J］.Сверхтвердыематериалы，1990（2），13～15.

［44］车云霞，申泮文.化学元素周期系［M］.天津：南开大学出版社，1999，87.

［45］M.Prutton，Surface Physics［M］.Oxford：Clarend on Press，1983，109.

［46］王矜奉，范希会，张承琚.固体物理概念和习题指导［M］.济南：山东大学出版社，2001，122.

［47］A.Pavlovska，E.Beuer，The Structure and Dynamics of Cryztal Surface at High Temperatures［J］.Applied Physics A：Solid and Surface，1990，51：172～182.

［48］黄昆.固体物理学［M］.北京；人民教育出版社，1979，91～94.

［49］Jean－Patrick Connerde，Highly Excited Atoms［M］.詹明生，王谨译，高激发原子.北京：科学出版社，2003，341～342.

［50］王金斌，杨国伟.脉冲激光诱导液2固界面反应合成金刚石纳米晶中的结构相变模型［J］.高压物理学报，1999，13（2）：147－151.