一种两级供应商的混合循环取货模式研究
林纯肯,董宝力,程阳春
(浙江理工大学机械与自动控制学院,杭州310018)
一种两级供应商的混合循环取货模式研究
林纯肯,董宝力,程阳春
(浙江理工大学机械与自动控制学院,杭州310018)
针对由多级供应商构成的物流取货问题,为了进一步降低运输零部件的物流成本,在传统循环取货的基础上,设计了一种新型的混合循环取货模式。该模式考虑了两级供应商对运输成本的影响,因此设计了一种两级供应商混合循环取货成本模式,并运用Floyd改进算法对循环路径模型进行求解及优化。最后以某电动工具公司为优化实例,给出了混合循环取货的具体结果,且通过与传统循环取货的实际发生成本进行比较,以说明笔者给出模式的优越性,同时证明两级供应商的混合循环取货路径模型,能够有效地降低物流成本。
混合循环取货;Floyd改进算法;循环路径;两级供应商
循环取货是属于精益生产中一种拉动式的物流模式[1],在装配厂或RDC配送中心与一级供应商直接联系的基础上,通过规划和设计循环取货路径,保证了装配厂的零件及时供应并使其能够正常生产,最终实现供应链成本下降。围绕传统循环取货,国内外学者已经取得了一些研究成果。Chauah等[2]建立了循环取货运行的数值理论模型,探讨循环取货实际运行中各个变量对库存-成本关系曲线的影响。Berman等[3]针对供应链中备受关注的运输和库存问题建立了启发式算法及拉格朗日松弛等数学模型进行分析,得到了运输规划和库存成本最小化的入厂物流模式。汪安静等[4]构建了循环取货物流运作模式的取货路径数学模型,在约束条件下运用C-W算法获得符合满意解。王晓博[5]根据电子商务配送网络及配送策略侧重点的不同,建立了基于时间—成本的分散型配送中心选址模型和基于服务—成本的混合型配送中心选址模型,从而确立最有效选址方案,同时对车辆调度优化和运输路径规划的问题进行了研究。以上研究,只是单一地将一级供应商作为元素进行考虑,可以发现车辆在循环取货点仅发生装载活动,这就降低了时间的价值。
本文在传统循环取货的基础上,通过考虑多级供应商运输因素,将直接供应商与间接供应商覆盖到整个循环取货过程中,提出了一种两级供应商的混合循环取货模式且建立了数学模型,利用改进的Floyd算法[6]对其进行求解。这种混合循环取货能够更好地组织装配厂入场物流,还能兼顾多级供应商的物料供应。这将大幅度地缩短装配厂和供应商产品的生产周期,并且通过共同承担循环取货费用,降低各方的物流成本,提高时间效益,从而实现整体供应链的优化。
一、混合循环取货模式研究
传统循环取货模式是指生产制造商调度一辆运输货车按照一定的路径,并在设定好的时间,按照一定的规则到相互挨近的多个直接一级供应商SA,去获取其生产所需的零部件,然后运送至RDC配送中心或者直接送至装配厂的取货模式[7]。这种传统模式其优点在于能够确保装配厂所需的物料以少批量、多频次的形式发往RDC配送中心或装配厂,将库存控制在较低水平,同时省去了供应商车辆空车返回工厂的费用,进而让整车物流费用得到有效控制,实现总体供应链成本的降低。其缺点在于实施传统循环取货时,忽略了循环路径上存在的成本交叉性:在循环路径上或周围的间接供应商(如二级供应商)SB,可通过共同租用运载车辆及司机的方式来完成物料供应,间接供应商承担一定比例物流费,进而降低直接供应商的物流费用。这种共同承担物流费用的方式能够实现单趟整体供应链成本的降低。结合传统循环取货模式和传统送货制物流模式——供应商为需求商进行送货,本文提出了一种多级供应商的混合循环取货模式,如图1所示,其曲线表示供应商之间存在供应与被供应关系。

图1 传统循环取货与混合循环取货模式示意
混合循环取货继承了传统循环取货及送货制的特点,还具有以下4个特点。
(a)供应商的服务对象由原来的装配厂扩展到其他关联供应商。
(b)对装配厂或RDC配送中心来说,其承担费用的路径更短并通过为多级供应商代理取货,产生代理费用在一定程度上补偿循环取货发生的成本。
(c)对一级供应商来说,通过共同租用运载货车及司机,消除了原供应链上人员费用和运输车辆费用。
(d)对二级供应商来说,混合循环取货可以使得其库存保持在较低水平,空间成本将会减少且有效地完成对一级供应商的供货任务。
这一模式有效连接了RDC配送中心、一级供应商和多级供应商、装配厂三者,并发挥了时间的同步性,基于循环路径具有交叉性的前提下,添加二级供应商元素,发挥其为循环取货带来的成本降低的作用。
二、两级供应商的混合循环取货成本优化模型
传统循环取货路径只考虑循环路径必须路过每一个一级供应商,RDC配送中心负责全部循环路径上的运载费用,与之比较混合循环取货则添加了多级供应商元素,要求混合循环路径上必须途径一级和多级供应商,且多级供应商SB的取货顺序要优先级于相关一级供应商SA的取货顺序,RDC配送中心负责O点到相邻2供应商及一级供应商SA到二级供应商SB的运载费用,而一级供应商则承担对应二级供应商到一级供应商的运载费用。
假设条件如下:
(a)装配厂或者RDC配送中心,其零部件一级供应商及二级供应商须分布在同一个区块且供应商所提供的零部件是可以同车运输的[8]。
(b)在混合循环取货过程中,要保证每次在循环取货点发生装载/卸载活动时,其总装载体积不超过最大车载容积Vmax。
通过算法求得循环路径D最小值,最终实现混合循环取货的成本F(x)最优。
设置有向图U=(C,E),C={SAi、SBj}代表供应商集合,而且各级供应商之间,各级供应商与RDC配送中心的距离是已知的,E为任意2个循环取货点之间的弧。
根据上述分析,建立一种多级供应商的混合循环取货成本优化模型,参数如下:
K代表载物车辆的集合;
G代表所用供应商的总集合;
SAi与SBj分别代表任意的一级供应商与二级供应商;
O代表装配厂或者RDC配送中心;
DSAiO代表一级供应商在混合循环路径上以SAi为起始点到O点实际运输距离;
DSBjO代表二级供应商在混合循环路径上以SBj为起始点到O点实际运输距离;
DSAiSBj代表二级供应商SBj与其对应一级供应商SAi之间的实际运输距离;
VSAi代表载物货车在一级供应商SAi装载的物料体积;
VSBj代表载物货车在二级供应商SBj装载的物料体积;
Vmax代表载物货车的最大装载量;
R1代表载物货车在混合循环取货中的运输单价(暂不考虑不同批量、不同运输工具引起的成本);
R2代表一级供应商SAi和O协商的代理运输单价。
得到混合循环取货发生的总成本,目标函数如下:


所以,F(x)=

决策变量:
约束条件如下:
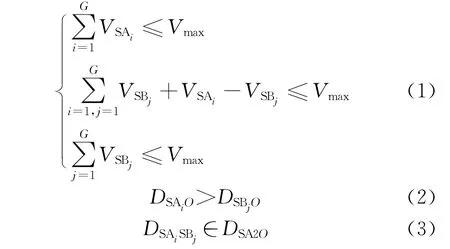

目标函数F(x)即为混合循环取货发生的总成本目标函数即整体物流成本。
约束条件(1)表示混合循环取货中任意供应商处,载物货车的运载体积不超过货车的最大装载量。约束(2)表示二级供应商SBj的装载顺序要优先于对应一级供应商SAi的装载顺序。约束(3)表示在混合循环取货路径上,以二级供应商SBj为起点到O点的最长路径中包含了以其他供应商为起点到O点的路径,保证了每个供应商点都能够被服务一次。约束(4)、(5)保证了混合循环取货是封闭循环。约束(6)、(7)表示了运载物料体积的非负数限制。
该模型实现的作用如下:1)通过为一级供应商SAi代理运载对应二级供应商SBj的物料,来向一级供应商SAi收取运输费用,以补偿整体供应链的费用。2)取消了二级供应商SBj向一级供应商SAi运输物料的车辆及人员。3)在一级供应商SAi同时发生卸载和装载事件,保证时间的有效性。4)整个混合循环取货的最终结果仍保证运输车辆的容载率保持满负荷水平,且不超出车载最大体积。5)在不影响装配厂或RDC配送中心的情况下,有效控制了间接供应商的库存量。
三、改进的Floyd算法
传统Floyd算法是针对所有点最短路径的一种求解算法,其基本原理是:将问题进行分解,首先找出最短距离[9]Dij,接着通过实际地图筛选出载物货车对应的行车线路。在循环取货路径上必须要经过若干个中间供应商点,i点与j点的最短距离存在2种情况,经过中间供应商w与不经过中间供应商w,可以令w=1,2,3…,m,其中m是供应商的数量。然后计算Dij与Diw+Dwj的数值,截止目前Diw+Dwj就是i点到j点,途径w的最短距离。通过不断迭代所有的w值,就能求出最短距离Dij。如图2所示,虚线表示两点不能直接连通:

图2 Floyd算法原理
本文涉及到多级供应商取货优先级问题,即二级供应商的取货顺序应该优先于对应的一级供应商,因此不能单纯地只考虑插入供应商点,来计算最优路径。改进的Floyd算法[7]能够在传统Floyd算法基础上,遵循多级供应商取货优先级来实现混合循环取货的路径优化,最终实现整体供应链成本最小。
求解步骤如下:
(1)设置原始距离矩阵D(0)=[d(0)ij]

(2)设置集合U1、U2。U1、U2内元素为对应关系。U1代表未被运输车辆访问的一级供应商点,U2代表未被运输车辆访问的二级供应商点。若U1、U2为空集,则迭代终止。若U1、U2为非空集,则跳转至步骤(3)。
(3)从U1中选择距离RDC最远的一家一级供应商SAi,建立起以RDC为起点,途径该一级供应商并最终返回RDC的初始循环路径,并且把一级供应商SAi从集合U1中删除。
(4)从U2中选择与上步骤对应一家二级供应商SBj,满足模型约束条件(2)插入到初始循环路径中的任意2个点(i,j)之间,同时计算造成的运输距离增量Δ(i,SBk,j)=diSBk+dSBkj-dij,选择最小Δ增量值作为最佳的插入位置并且把二级供应商SBj从集合U2中删除。
(5)从U1、U2中选取任意一一对应的一级供应商和二级供应商,满足约束条件(2)。分别插入到步骤(3)、(4)所构建的混合循环路径上,并依据最小Δ增量值,找出最佳插入位置。同时将元素从对应集合U1、U2中删除。
(6)重复步骤(5),满足模型约束条件(1),若D(w)=D(w+1)即Δ(i,w,j)=diw+dwj-dij=0,则迭代停止。否则,返回步骤(5),直至迭代结束。
改进的Floyd算法是针对具有不同优先级的多维数多顶点闭环,在多重约束条件下目前求解最短路径的有效算法。而一种多级供应商的混合循环取货模式是属于闭环运输,设定有始发点和终止点,且有明确的中间点,因此本文通过改进的Floyd算法来对模型进行求解。
四、模型仿真及成本比较
本文以某电动工具公司物流部门为研究对象,O为该工厂,SA1是O的上机壳、下机壳供应商,SA2是O的马达供应商,SA3是O的PCB电路板供应商,SA4是O的螺丝供应商,SA5是O的感应标签供应商,SA6是O的指示灯供应商。SB1是SA1、SA5的塑料供应商,SB2是SA2的铜线供应商,SB3是SA3的覆铜板供应商,SB4是SA4的碳钢供应商,SB5是SA5的敏感元件供应商,SB6是SA6的发光二极管供应商。各级供应商供货量及对应关系如表1所示。

表1 供应商的供货量
装配厂、一级供应商、二级供应商三者之间的距离(单位:km),如表2所示。

表2 装配厂与各级供应商的距离单位:km
运用Matlab进行数据仿真,设置矩阵A为邻接矩阵,对角线上都是0,其他位置上数字是指两点之间的距离,其中inf是∞的意思即两点之间未直接连通,n=length(D),设定n为矩阵D的长度,然后进行二次循环初始化循环路径,之后便进行三重循环得到更新路径,直至所有供应商点被遍历一次,得到最优路径图3。
最优路径为:装配厂—SB1—SB2—SA2—SA1—SB3—SA3—SB4—SB5—SA4—SA5—SB6—SA6—装配厂,混合循环路径上货车经过每个节点并无出现重叠交叉的路径。计算该混合循环取货发生的成本并与传统循环取货成本进行比较。计算过程如下:

图3 仿真最优路径
R1运输单价为5元/(km·m3);
R2一级供应商SAi和R协商好的代理运输单价为10元/(km·m3);
车体最大容积Vmax=45.5m3通过仿真得到混合循环取货的发生成本为:

传统循环取货的成本,其中dSAiO指传统循环取货下,一级供应商到装配厂的实际运输距离,查询表2可知:

在混合循环模式下,单趟循环取货可节约成本4 276元。
五、结束语
本文在传统循环取货模式的基础上,考虑了次级供应商取货问题,以此提出了两级供应商的混合循环取货模式。在此模式中RDC配送中心与一级供应商统一承担运载费用,供应商的供货对象由装配厂衍生到其他供应商,且供应商之间建立供货关系,使得各自承担物流成本降低。根据约束条件本文设计了多级供应商循环取货成本模型并利用改进的Floyd算法来针对模型进行求解,最后以某电动工具公司为实例,计算出混合循环取货成本,并与传统循环取货成本进行比较,进一步说明了混合循环取货的合理性。本文模型中尚未考虑时间窗约束、运输批量等因素。在未来研究中,可加入时间窗等约束,建立一种自适应混合循环取货模式,进一步分析动态供应链及时性等问题。
[1]汪金莲,蒋祖华.汽车制造厂零部件入厂物流的循环取货路径规划[J].上海交通大学学报,2009,(11):1703-1708.
[2]Chuah K H,Yingling J C.Routing for a just-in-time supplypickup and delivery system[J].Transportation Science,2005,39(3):328-339.
[3]Berman O,Wang Q.Inbound logistic planning:minimizing transportation and inventory cost[J].Transportation Science,2006,40(3):287-299.
[4]汪安静,龚本刚.基于CW算法的汽车零部件循环取货车辆路径优化研究[J].安徽工程科技学院学报:自然科学版,2010,25(2):91-94.
[5]王晓博.电子商务下物流配送系统优化模型和算法研究[D].哈尔滨:哈尔滨工业大学,2008.
[6]姜舒曼.汽车制造企业零部件入场物流循环取货路径优化:以华中某汽车制造企业为例[J].物流工程与管理,2013(3):76-79.
[7]陈建华,帅 颖,林东波,等.三级供应链循环取货成本优化模型[J].武汉理工大学学报:信息与管理工程版,2009,31(5):838-841.
[8]曹 强,张明智,李志强,等.CTI中车辆实时最佳路径搜索算法设计与实现[J].系统仿真学报,2009,21(21):6777-6780.
[9]王 荣,江 东,韩 惠.基于Floyd方法的最短路径算法优化算法[J].甘肃科学学报,2013,24(4):110-114.
Study on Mixed Milkrun Mode for Two-Level Suppliers
LIN Chun-ken,DONGBao-li,CHEN Yang-chun
(School of Mechanical Engineering and Automation,Zhejiang Sci-Tech University,Hangzhou 310018,China)
In allusion to logistics goods taking consisting of multi-level suppliers,a new mixed milkrun mode is designed on the basis of traditional milkrun in order to further reduce logistics cost of transportation parts.This mode takes into account of effects of two-level suppliers on transportation cost,so mixed milkrun mode involving two-level suppliers is designed.Besides,improved Floyd algorithm is applied to solve and optimize circulation path model.Finally,specific results of mixed milkrun are provided through regarding an electric tool comoany as an example.The superiority of the mode is shown through comparing with actual cost of traditional milkrun.Meanwhile,it is proven that the mixed milkrun mode can effectively reduce logistics cost.
mixed milkrun mode;improved Floyd algorithm;circulation path;two-level suppliers
TP311
A
(责任编辑:张祖尧)
1673-3851(2014)06-0460-05
2014-05-09
浙江省自然科学基金资助项目(LY12G02015)
林纯肯(1990-),男,浙江温州人,硕士研究生,主要从事精益生产的研究。
董宝力,电子邮箱:tydbl@zstu.edu.cn

