基于频谱和瞬时频率的雷达信号识别方法

马宁， 马亮

（上海无线电设备研究所，上海 200090）

基于频谱和瞬时频率的雷达信号识别方法

马宁， 马亮

（上海无线电设备研究所，上海 200090）

随着雷达技术的不断发展和应用，雷达信号识别对于雷达对抗和电子侦察具有重要意义。针对常用雷达信号的识别问题，提出了一种基于频谱和瞬时频率的雷达信号识别方法，通过定义的四个用于区分不同信号的特征值，可以对于常用的七种雷达信号进行有效识别。仿真实验证明了该方法的有效性和可行性。

雷达信号识别；频谱；瞬时频率；线性拟合

0 引言

随着现代电子战对抗的日趋激烈，雷达设备配置使用的范围不断扩大，雷达信号形式越来越复杂多变，雷达信号脉内特征识别成为电子情报（ELINT）和电子支援（ESM）系统中的重要组成部分[1]。通过对雷达信号细微特征的提取和分析，可以得到信号的调制特性以及一些脉内参数的估计，从而可以从敌方发射的信号中检测有用的信息，并且与其它方式获取的信息综合起来，引导我方做出及时、有效、准确的反应对整个雷达对抗起着至关重要的作用[2-3]。

目前国内外学者们研究了不少对于雷达脉内信号进行识别的方法，如时域自相关法[4]、时频变换法[5]、小波变换法[6]、神经网络[7]、模糊函数[8]等，它们在相应条件下能够较为准确地提取脉内调制特征，但目前这些算法针对的雷达信号识别种类较少，无法面向多种不同脉内调制雷达信号的识别。文献[9，10]提出了基于时频原子特征的雷达信号识别方法，以时频原子和信号内积的绝对值作为判断识别的输入特征，主要对线性调频信号和相位编码信号进行识别。文献[11]提出了一种雷达信号脉内调制类型识别方法，通过时域累加、时频变换以及瞬时自相关相结合的方法来实现调频信号和调相信号的细微识别。文献[12]介绍了频率键控-二相编码信号的识别方式，对复合调制信号进行了识别，针对的是特定雷达信号的识别。

本文主要介绍了对七种常见雷达信号进行识别的方法，该方法目前已经在硬件上实现并获得验证。七种雷达信号分别为单载频信号、频率分集信号、线性调频信号、非线性调频（抛物线型）信号、V字型调频信号、二相编码信号、四相编码信号。其中非线性调频（抛物线型）信号是指其频率随时间的变化规律呈抛物线型的非线性调频信号，而V字型调频信号则为其频率随时间的变化规律呈V字型的调频信号。

1 信号识别的特征值

1.1 识别预处理

将感兴趣的射频频带下变频到中频，以采样频率fA/D进行中频带通采样，然后进行16信道化，每个子信道输出的数据率为fs=（fA/D）/16，在每个子信道中进行信号检测与识别。

设第l个子信道输出为xl[n]，0≤n≤N-1，N表示信号长度，其瞬时相位为

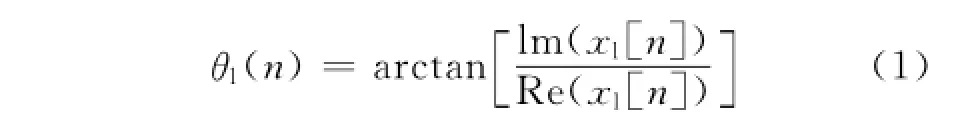
对其进行相位去绕，去除2π模糊，得到其瞬时频率

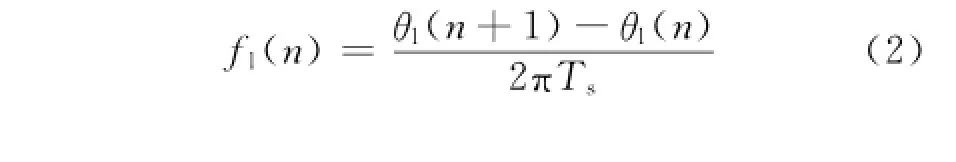
其中：

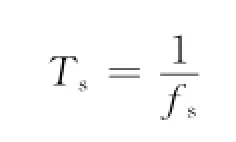
需要识别的常见雷达信号包括以下七种：

a）单载频信号；

b）频率分集信号；

c）线性调频信号；

d）非线性调频（抛物线型）信号；

e）V字型调频信号；

f）二相编码信号；

g）四相编码信号。

为了对上述七种雷达信号进行识别，首先定义四个用于区分不同信号的特征值，分别为检测离散谱线的特征值φ1、检测是否直线的特征值φ2、检测斜率是否为零的特征值φ3、检测非线性调频（抛物线型）信号的特征值φ4。

1.2 检测离散谱线的特征值φ1

为了区分频谱中最高谱线处是否存在明显的离散单频谱线，可以通过频谱最高谱线和其周围谱线的比值来设定特征值进行检测。

对xl[n]进行快速傅里叶变换（FFT）后得到Xl[k]，搜索得到频谱中的最大值和其对应的位置，分别记为ma和a。计算频谱中最大值点周围2m个点的平均值（不包括最大值点和其左右相邻两点），即

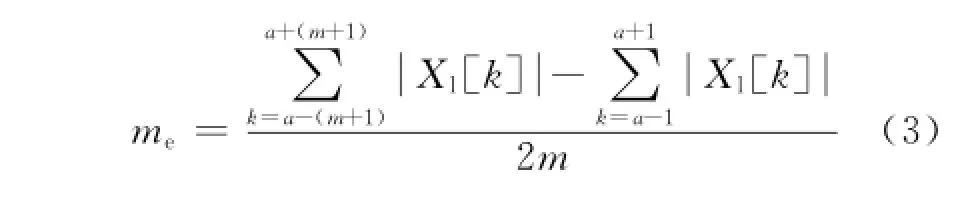
式中：m，k∈Z＋；0≤k≤N-1。为了防止频谱泄露引起漏检，此处消除了最高谱线的左右相邻谱线的影响。可以将k在[0，N-1]内循环取值，对最高谱线出现在频谱两端的特殊情况进行处理。

比较最大值点和其周围2m个点的平均值可以用来区分是否存在离散单频谱线，即选取特征值为

若存在离散单频谱线，则特征值φ1较大；若不存在离散单频谱线，则特征值φ1较小。显然，特征值φ1可以反映谱线的突出程度，当它大于某阈值时可以认为在最高谱线处检测到离散单频谱线，从而可以设置一个阈值φth1，当φ1＞φth1时，判断频谱中最高谱线处存在离散单频谱线；当φ1＜φth1时，判断频谱中最高谱线处不存在离散单频谱线。

1.3 检测是否直线的特征值φ2

为了区分瞬时频率曲线是否呈直线，可以先求出信号的瞬时频率，然后对其进行线性拟合，比较拟合直线与实际瞬时频率曲线之间的差值可以进行检测。

曲线拟合是指用连续曲线近似地刻画或比拟平面上离散点组所表示的坐标之间的函数关系。在数值分析中，曲线拟合就是用解析表达式逼近离散数据，即离散数据的公式化。若待定函数或解析表达式是线性的，就称为线性拟合。最小二乘法是一种较为简便的计算方法，可以用于曲线拟合，它通过最小化误差的平方和寻找数据的最佳函数匹配。

由式可以求出信号的瞬时频率，对其进行线性拟合，即求得

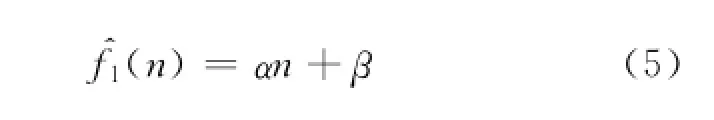
式中：α为拟合直线的斜率；β为拟合直线的截距。

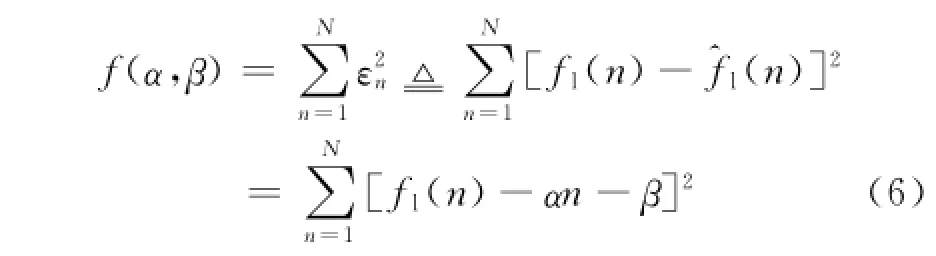
最小，可以求解如下联立方程

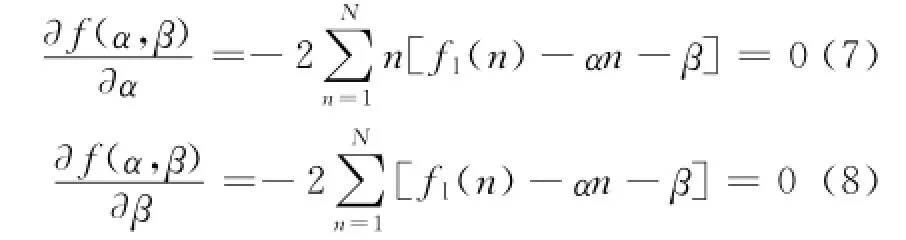
求解式和式可得

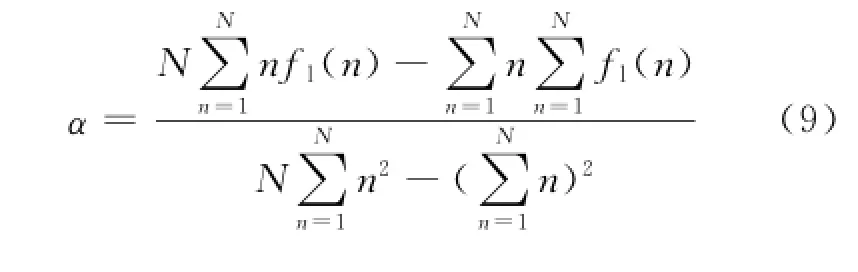
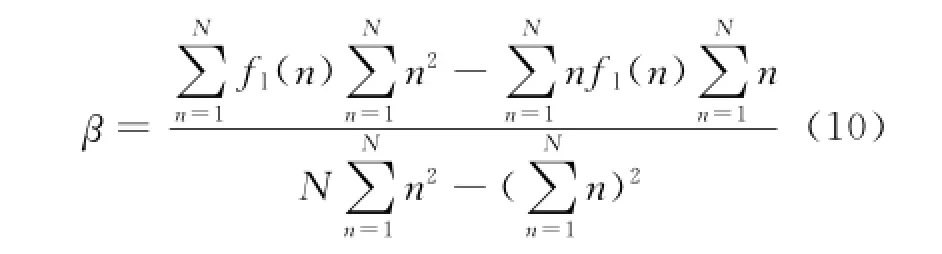
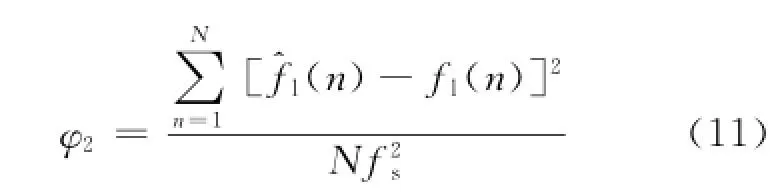
特征值φ2可以反映瞬时频率曲线是否呈直线，当它小于某阈值时可以认为瞬时频率曲线呈直线。从而可以设置一个阈值φth2，当φ2＜φth2时，判断瞬时频率曲线呈直线；当φ2＞φth2时，判断瞬时频率曲线不呈直线。

1.4 检测斜率是否为零的特征值φ3

可以很容易推导得出，V字型调频信号瞬时频率的线性拟合曲线的理论斜率为零。为了对V字型调频信号进行识别区分，选取特征值φ3=｜α｜用于判断瞬时频率的线性拟合曲线的斜率是否为零。可以设置一个接近于零的阈值φth3，当φ3＜φth3时，判断瞬时频率的线性拟合曲线的斜率为零；当φ3＞φth3时，瞬时频率的线性拟合曲线的斜率不为零。

1.5 检测非线性调频(抛物线型)信号的特征值φ4

为了区分线性调频信号和非线性调频（抛物线型）信号，理论上可以通过检测直线的特征值φ2进行区分。然而非线性调频（抛物线型）信号的二次曲率较小时，在低信噪比情况下出现误判的概率会偏大。因此为了区分上述两个信号，根据两种信号频谱的特点选取频谱最大值与次大值之间的比值可以进行检测，为了防止频谱泄露的影响，次大值的选取为频谱最大值及其左右各10个点置零后的最大值。若为线性调频信号，则频谱的最大值与次大值之间的比值φ4较小；若为非线性调频（抛物线型）信号，则频谱的最大值与次大值之间的比值φ4较大。可以设置一个阈值φth4，当φ4＜φth4时，判断为线性调频信号；当φ4＞φth4时，判断为非线性调频（抛物线型）信号。

2 信号识别流程

上述七种雷达信号识别流程图如图1所示，识别过程步骤如下：

a）第一步，首先对需要识别的接收信号进行FFT获得频谱，通过检测离散谱线的特征值φ1来区分出频谱最高谱线处是否存在离散单频谱线，若频谱的特征值φ1大于阈值φth1则判断接收信号为单载频信号或频率分集信号，否则为其它五种雷达信号；

b）第二步，若根据步骤一判决为单载频信号或频率分集信号，则进一步求出待识别接收信号的瞬时频率，并对其进行线性拟合，通过检测直线的特征值φ2来区分信号瞬时频率曲线是否呈直线，若信号瞬时频率的特征值φ2小于阈值φth2，则判断接收信号为单载频信号，否则为频率分集信号；

c）第三步，若根据步骤一判决为其它五种雷达信号，则将信号平方，对其进行FFT得到二次方频谱，通过检测离散谱线的特征值φ1来区分出二次方频谱最高谱线处是否存在离散单频谱线，若二次方频谱的特征值φ1大于阈值φth1则判断接收信号为二相编码信号，否则为其它四种雷达信号；

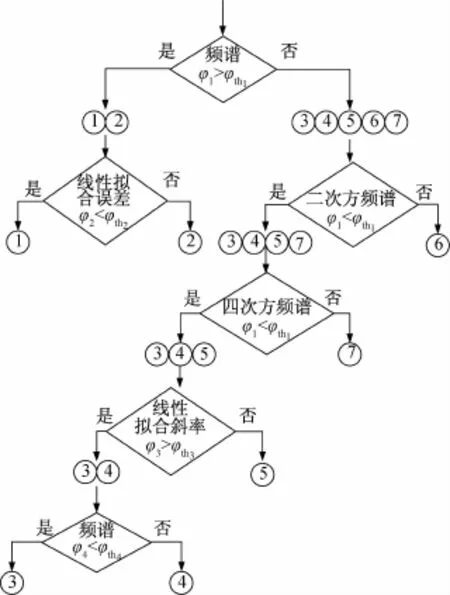
图1 雷达信号识别流程图

d）第四步，若根据步骤三判决为其它四种雷达信号，则将信号四次方，对其进行FFT得到四次方频谱，通过检测离散谱线的特征值φ1来区分出四次方频谱最高谱线处是否存在离散单频谱线，若四次方频谱的特征值φ1大于阈值φth1则判断接收信号为四相编码信号，否则为其它三种雷达信号；

e）第五步，若根据步骤四判决为其它三种雷达信号，则求出信号的瞬时频率，并对其进行线性拟合，通过检测斜率是否为零的特征值φ3来区分信号瞬时频率的斜率是否接近于零。若信号瞬时频率的特征值φ3小于阈值φth3则判断接收信号为V字型调频信号，否则为其它两种雷达信号；

f）第六步，若根据步骤五判决为其它两种雷达信号，则再次对信号的频谱进行分析，通过特征值φ4来检测非线性调频（抛物线型）信号，若信号频谱的特征值φ4小于阈值φth4则判断接收信号为线性调频信号，否则为非线性调频（抛物线型）信号。

3 仿真结果

为了验证算法的有效性，在不同信噪比下对上述七种雷达信号的识别进行了仿真。中频信号位于250 M Hz～450 M Hz频带中，以采样频率fA/D=500 MHz进行中频带通采样，加入高斯白噪声，然后信道化，每个子信道输出的数据为fs=（fA/D）/16=31.25 M Hz，中频信号脉宽为200 µs，线性调频信号、非线性调频（抛物线型）信号和V字型调频信号带宽为5 MHz，二相与四相编码信号子码宽度为0.2µs。信噪比（SNR）步进为2 dB，每个信噪比下进行200次蒙特卡罗实验仿真。仿真中各个阈值的选取采用经验阈值，其中阈值φth1取值为10，阈值φth2取值为0.5 Hz，阈值φth3取值为3×105Hz/s，阈值φth4取值为1.2。

图2给出了七种雷达信号在不同信噪比下的正确识别率。可以看出各种中频端接收雷达信号在SNR≥-4 d B时识别率均达到95%以上，说明在较低信噪比下本文提出的雷达信号识别方法具有较高的识别率，是一种比较有效的雷达信号识别方法。

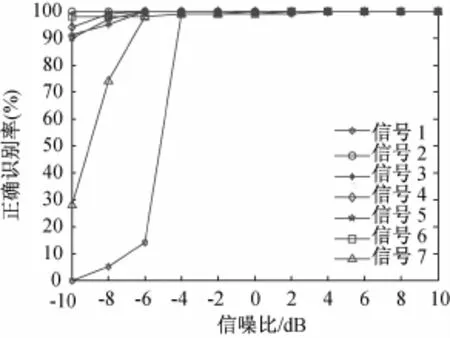
图2 雷达信号正确识别率

为了分析上述雷达信号在识别过程中各特征值的误判情况，表1给出了SNR=-8 d B时各种信号200次蒙特卡罗实验识别结果的统计数据。其中横排为待识别的接收信号，竖列为信号的识别结果。

从表1可以看出，在SNR=-8 d B时单载频信号基本被误判为频率分集信号，分析其原因在于随着信噪比的降低，噪声会逐渐增大，从而线性拟合曲线与实际瞬时频率曲线之间的误差也会增大，超过阈值φth2时就会误判为频率分集信号，也就如表1所示。可以通过增加阈值φth2来减小此处的误判率，然而如果φth2过大，则可能会将高信噪比时的频率分集信号误判为单载频信号，因此对于φth2的选择也不能过大，此处可以对阈值φth2进行适当的增大调整。表1中另外一个误判率比较高的是四相编码信号，它在SNR=-8 dB时有一定比例会被误判为线性调频信号或非线性调频（抛物线型）信号。通过图1可以分析得到，此处的误判原因在于四次方频谱的离散单频谱线阈值φth1取值过高，且此处线性调频信号或非线性调频（抛物线型）信号并没有被误判为四相编码信号，可以将此处的阈值φth1取值适当调整变小。事实上，各个特征值的阈值应当优先保证各种信号在高信噪比的情况下能得到有效的识别，在此基础上再进行适当的调整来提高低信噪比下的识别率，也可以在预先估计了信噪比的情况下，对同一个特征值在不同信噪比下设置不同的门限来提高识别率。

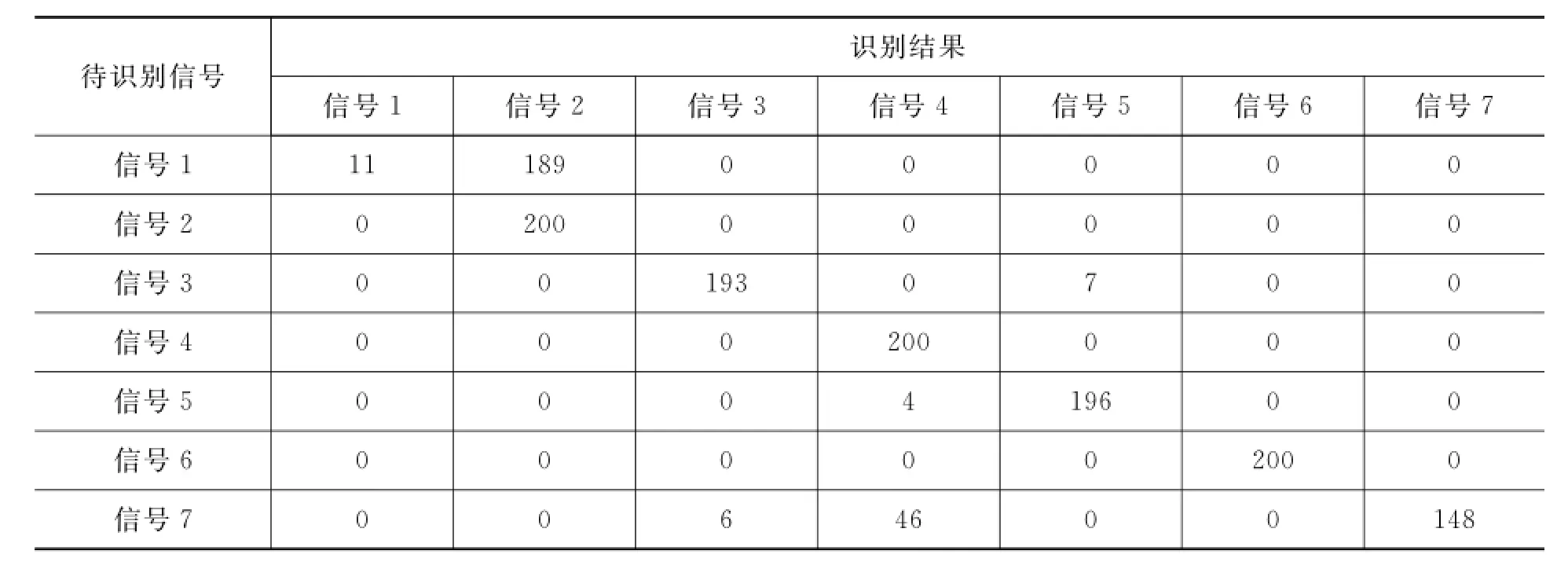
表1 七种雷达信号在SNR=-8 dB时的识别结果

4 结论

随着雷达技术的迅速发展和大量运用，如何从密集复杂的信号环境中分选和识别出特定的雷达信号，已成为雷达信号处理中的一个重要内容，对于电子侦察对抗具有重要意义。本文提出了一种基于频谱和瞬时频率的雷达信号识别方法，主要定义了四个用于区分不同信号的特征值，采用这些特征值进行雷达信号识别过程，在较低信噪比下具有较高的识别率，是一种有效的常用雷达信号识别方法。这种方法算法简单，实时性较好，适合于工程应用。

[1] Kawalec A，Owczarek R.Specific Emitter Identification Using Intrapulse Data[C].Poland：Proceedings of 15th International Conference on Microwaves，Radar and Wireless Communications，2004，2：435-438.

[2] Jan M.Specific Emitter Identification[D].Poland：International Radar Symposium，2008：1-4.

[3] 赵慧昌，张淑宁.电子对抗理论与方法[M].北京：国防工业出版社，2010.

[4] 翟孝霏，刘雅轩，陈涛，等.一种快速雷达信号脉内调制识别分析方法[J].现代雷达，2012，34（6）：16-19.

[5] Gustavo L R，Jesus G，Alvaro S O.Digital Channelized Receiver Based on Time-Frequency Analysis for Signal Interception[J].IEEE Transactions on Aerospace and Electronic Systems，2005，41（3）：879-898.

[6] Delpart N.Asymptotic Wavelet and Gabor Analysis：Extraction of Instantaneous Frequencies[J]. IEEE Transaction on Information Theory，1992，38（3）：644-664.

[7] Shieh Ching-sung，Lin Chin-teng.A Vector Neural Network for Emitter Identification[J].IEEE Transactions on Antennas and Propagation，2002，50（8）：1120-1127.

[8] 李林，姬红兵.基于模糊函数的雷达辐射源个体识别[J].电子与信息学报，2009，31（11）：2546-2551.

[9] 王希勤，刘婧瑶，孟华东，等.一种基于时频原子特征的雷达辐射源信号识别方法[J].红外与毫米波学报，2011，30（6）：566-570.

[10] 张昕然，谢红.一种低信噪比下基于时频原子的复杂调制雷达信号分选方法[J].应用科技，2013，40（3）：50-53.

[11] 司伟建，刘海朝，郝鑫.雷达信号脉内调制识别及其FPGA实现[J].弹箭与制导学报，2012，32（6）：147-150.

[12] 宋军，刘渝，王旭东.FSK/BPSK复合调制信号识别与参数估计[J].电子与信息学报，2013，35（12）：2868-2873.

A Method for Radar Signal Recognition Based on the Spectrum and Instant Frequency

MA Ning， MA Liang
（Shanghai Radio Equipment Research Institute，Shanghai 200090，China）

Along with the development and the application of radar technology，radar signal recognition is significant for radar countermeasure and electronic reconnaissance.In order to identify common radar signals，a method for radar signal recognition based on the spectrum and instant frequency is proposed.Four characteristic values are defined to distinguish different signals with this method.Seven common radar signals can be identified effectively by the defined characteristic values.The simulations are carried out to demonstrate the effectiveness and feasibility of this proposed method.

radar signal recognition；frequency spectrum；instant frequency；linear fitting

TN957.52

A

1671-0576（2014）03-0016-05

2014-06-10

马 宁（1985-），男，博士，工程师，主要从事雷达信号处理技术研究。