基于范数IOWGA算子的大学生就业信心指数组合预测模型
石琼强,杨桂元
石琼强,杨桂元
(安徽财经大学 统计与应用数学学院,安徽 蚌埠 233030)
自上世纪90年代以来,我国大学毕业生人数快速增长,“大学生就业难”问题日益突出,已经成为高等教育界乃至整个社会共同关注的焦点. 那么,作为当事人的大学生对于就业的看法如何?大学生对于就业的预期究竟几何?对于就业,他们是否充满信心?如何增加大学生的就业信心?如何对大学生的就业观进行定量研究?诸如此类的问题需要进行系统的研究. 为此,许多学者试图建立衡量大学生就业信心的指数或者指标体系,并以此为基础对大学生的就业信心进行定量研究.
近年来,大部分学者致力于大学生就业信心指数或者指标建立的系统研究[1-2],而对于指数的进一步分析与预测却相对较少. 对于大学生就业信心指数的预测可以在一定程度上了解大学生就业信心的变化趋势,为国家和学校制定适合社会需要的人才培养计划提供科学的依据,从而改善“大学生就业难”问题.
在CNKI搜索大学生就业信心指数预测发现2013年仅有127篇相关文章,文献[3-4]建立灰色神经网络模型和文献[5]建立GM(1,N)模型对大学生就业指数预测. 文献[3-5]等虽然从不同的角度考虑并建立不同的模型对大学生就业信心指数进行预测,但都有预测方法单一的缺陷,势必会造成预测结果的片面性,预测效果不尽如人意.
1 各种单项预测方法和基于范数的IOWGA算子组合预测模型介绍
1.1 GM(1,N)模型[5-6]
GM(1,N)模型即多变量一阶常系数微分方程的灰色预测模型.
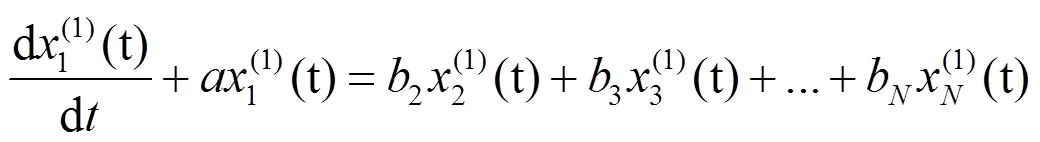
求解方程(1),得到GM(1,N)的预测公式:
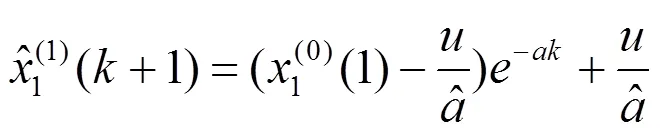
1.2 单指数平滑模型
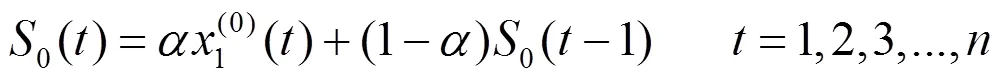
1.3 ARMAX模型[7]
包含个自变量的ARMAX(,)模型可以表示为:
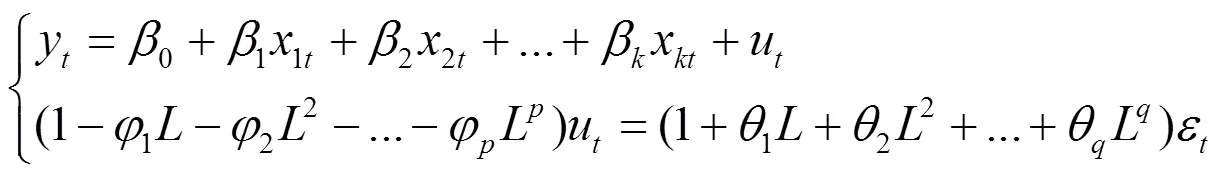
1.4 基于范数的IOWGA算子组合预测模型
1.4.1 IOWGA算子[8]
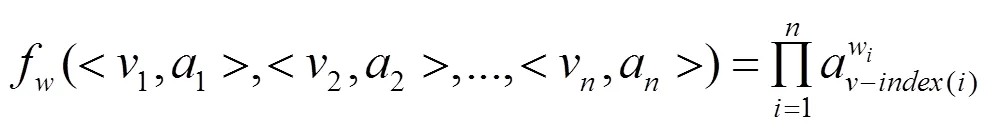
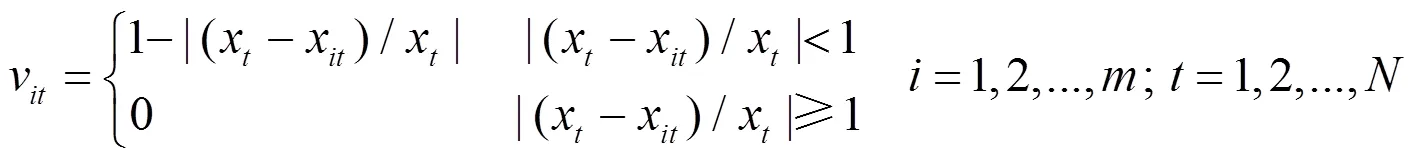
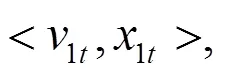

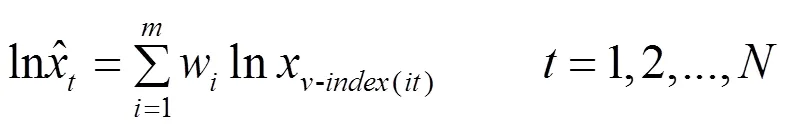
模型1
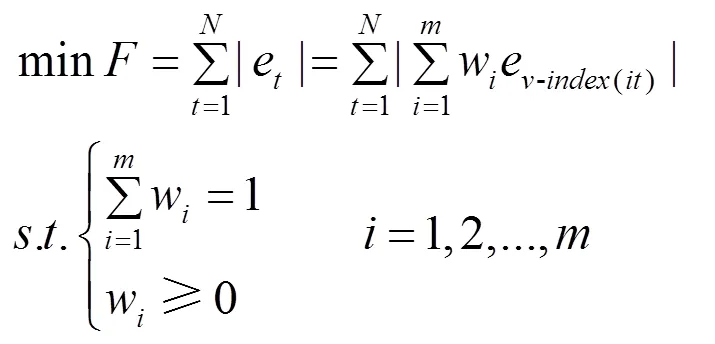
模型2
2 实证分析
本文引用文献[3-4]中山东省德州市某高校2000—2012年大学生就业信心指数数据(表1)进行实证分析. 如表1所示,本文讨论的影响全局信心指数的因素主要有3个,即经济景气指数、性别与学历层次,总共包含五个指标变量,即经济景气指数、男生信心指数、女生信心指数、本科生信心指数和专科生信心指数. 这里主要探讨对全局信心指数的预测.
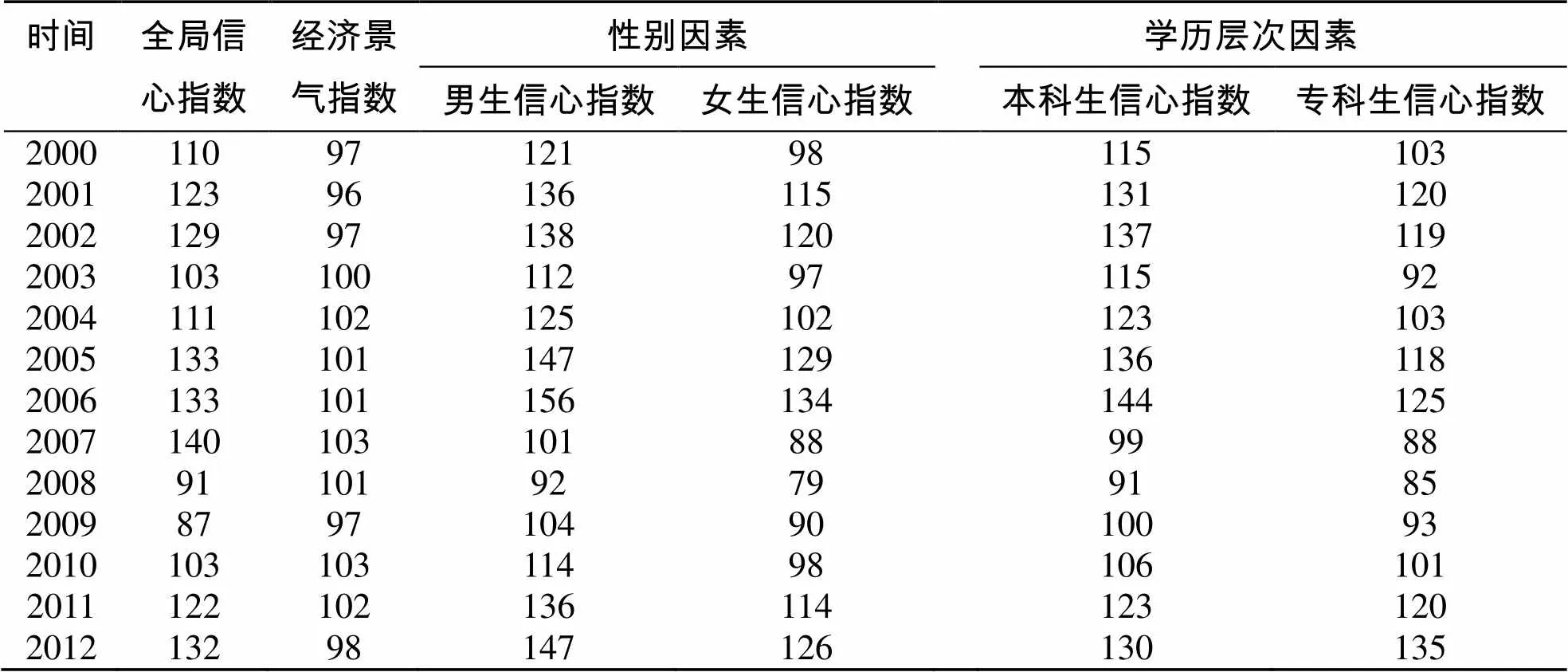
表1 2000—2012年大学生就业信心指数
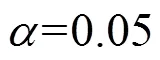
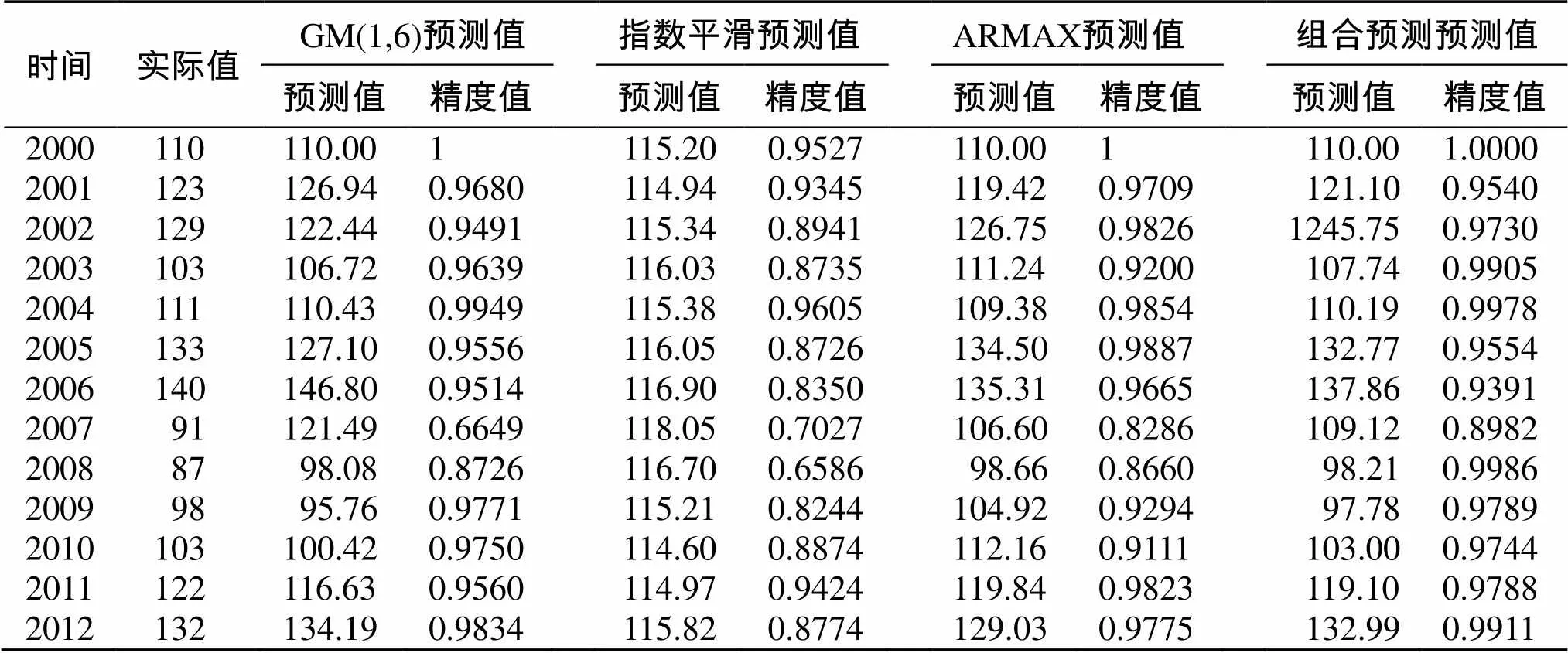
表2 全局信心指数实际值与各种单项预测和组合预测值预测值
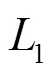
表3 预测效果评价指标体系
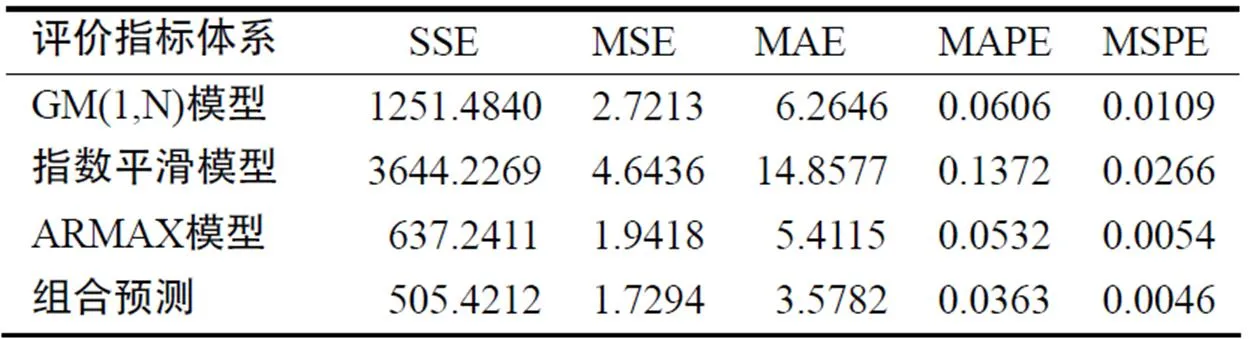
为了进一步对组合预测模型的有效性进行评价,本文选取平方和误差(SSE)、均方误差(MSE)、平方绝对误差(MAE)、平均绝对百分比误差(MAPE)和均方百分比误差(MSPE)5个指标作为评价指标,计算结果如表3所示. 结果显示,从SSE、MSE、MAE、MAPE和MSPE5个评价指标而言,本文提出的组合模型都优于各种单项预测方法.
3 结语
[1] 周红霞. 大学生就业信心状况调查与对策分析[J]. 东北师大学报: 哲学社会科学版, 2011(3): 214-217.
[2] 童光荣, 高 杰. 大学生就业指数系统研究[J]. 数量经济技术经济研究, 2003(6): 93-96.
[3] 杨光军. 灰色理论和BP神经网络在大学生就业信心指数预测中的应用[J]. 数学的实践与认识, 2013, 43(13): 62-67.
[4] 杨光军. 灰色神经网络在大学生就业信心指数预测中的应用[J]. 计算机系统应用, 2013, 22(8): 190-193.
[5] 杨光军. 基于GM(1, N)的大学生就业信心指数预测中的应用[J]. 轻工科技, 2013(6): 174-175.
[6] 李娟飞, 陈 静, 杜丽英, 等. GM(1,1)和GM(1, N)模型在GDP预测中的应用比较[J]. 科技信息: 高校讲坛, 2008(20): 498-499.
[7] 高铁梅. 计量经济分析方法与建模[M]. 北京: 清华大学出版社, 2009.
[8] 周礼刚, 陈华友, 韩 冰, 等. 基于对数灰关联度的IOWGA算子最优组合预测模型[J]. 运筹与管理, 2010, 19(6): 33-38.
[10] 杨桂元, 唐小我, 马永开, 等. 最优加权几何平均组合预测方法研究[J]. 统计研究, 1996(2): 55-58.
SHI Qiongqiang, YANG Guiyuan
(School of Statistics and Applied Mathematics, Anhui University of Finance and Economics, Bengbu 233030, China)
2014-01-09
国家社科基金项目(12BTJ008); 安徽财经大学研究生创新基金项目(ACYC2013052)
石琼强(1990— ), 男, 安徽安庆人, 安徽财经大学统计与应用数学学院硕士研究生; 杨桂元(1957— ), 男, 安徽萧县人, 安徽财经大学统计与应用数学学院教授, 硕士生导师, 主要研究方向:数量经济学.
F201;F224.0
A
2095-4476(2014)02-0008-04
(责任编辑:饶 超)

