不同粒径级砂土渗透特性试验研究

苏立君，张宜健，王铁行

（1.西安建筑科技大学 西部建筑科技国家重点实验室（筹），西安 710055；2.中国科学院水利部成都山地灾害与环境研究所 中国科学院山地灾害与地表过程重点实验室，成都 610041；3.浙江精工钢结构集团有限公司，浙江 绍兴 312030）

1 引 言

作为建筑材料、坝体反滤料、地基处理用料，随着岩土工程学科的发展，砂土在现实生活、生产过程中的应用愈发广泛。渗透性是砂土的重要工程性质之一，渗透系数是分析土中动水压力和土工结构物在降雨及水位变化作用下稳定性所必需的参数。影响砂土渗透性的因素有很多，比如土体密实程度、土颗粒自身特性、流体性质等。确定渗透系数通常有试验和经验公式两种方法，通过渗透试验测定渗透系数的过程相对较为复杂，并且由于试样饱和历时较长，试验操作误差等均会导致结果产生一些偶然性的偏差。经验公式法相比试验方法较为简便、易操作，但既有的经验公式都有一定的适用范围，实际使用起来受到的限制比较多。因此，选择恰当的试验方法确定渗透系数的主要影响因素，并给出准确合理的经验性公式具有重要意义。

鉴于渗透系数的重要性，自Darcy对两种均匀砂质滤床进行试验并提出达西定律v ki=−以来[1]，国外学者针对砂土的渗透特性做过诸多的研究，相继提出了 Terzaghi公式[1]、Hazen公式[2]、Kozeny公式[3]、扎乌叶布列公式（K18，18代表 18°C）[4]等，Hansen[5]、Chapuis[6]等则针对上述模型的适用范围及适用情况作出进一步的分析，在达西定律的基础上建立了一系列较为全面的砂土渗透理论。国内在无黏性土渗透性领域的研究相对较晚，较为细致的研究以20世纪80年代南京水利水电科学研究院为代表，提出了砂土渗透的平均孔隙直径模型[7]。此外，朱崇辉[8]、杨靖[9]、崔荣芳[10]等针对无黏性土的渗透性从不同角度也做了进一步深入的研究。综合国内外的研究发现，渗透性的大小与土体的特征粒径、密实程度、流体黏滞度有着密切关系，不同学者选择不同参量给予了一定的定量研究。但天然砂土作为一种混合料，除了颗粒大小、形状不同外，其内部结构、孔隙通道也较为复杂，前人的诸多研究均建立在混合料基础之上，这种研究均掺杂有颗粒组成这一不确定性因素的影响，导致针对多粒径混合土料而无法单独对影响渗透性的各个因素进行定量化研究，因此，诸多因素中何种因素为影响渗透系数的主要因素、各因素对渗透性的影响规律尚不明确。鉴于前人渗透模型假设与天然砂土差异较大，作者通过对天然砂土筛分，首先选择不同粒径的单一粒级土料作为研究对象，从粒径级层面上研究影响砂土渗透系数的主要因素，而后将所得结论向多元化粒径级土料过渡，针对天然砂土作进行深入的研究。

2 试验材料及试验过程

2.1 试验材料的物理特性

试验中使用的砂土材料来源于西安灞河流域的河沙，具有天然砂土颗粒的表面形状，与实际工程用砂表面特性一致。将所取天然河沙筛分可得其颗粒累计级配曲线和颗粒分布曲线如图1所示，颗粒累计曲线稍陡、光滑连续且无平台段表明颗粒较为均匀。由颗粒分布曲线可知，该天然砂土的主要粒径区间分布在0.25～0.50 mm、0.5～1.0 mm两个区段。试验所用土样是将天然砂过圆孔标准筛，分别得到 0.10～0.25、0.25～0.50、0.5～1.0、1～2、2～5 mm共5个粒径区间，各5～10 kg，并通过比重瓶法测定各粒径区间土颗粒的相对密度，所得各粒径级相对密度大小如表1所示。

图1 天然砂土的颗粒累计曲线和颗粒分布曲线Fig.1 Particle accumulated curve &particle sized distribution curve of natural sand

表1 各粒径级砂土颗粒的相对密度值Table 1 Sand particle’s relative density of each particle size fraction

2.2 试验过程

鉴于砂土渗透性较好，本研究采用常水头渗透试验。试验所用仪器为基姆式渗透仪（70型渗透仪），该仪器内径约为100 mm，筒高约400 mm，试验装样高度约为 28 cm左右，所测土样高度为10 cm[11]，与三轴应力式渗透仪、南55型渗透仪相比，减小了试样尺寸效应的影响。试验时取不同粒径级的土料3～4 kg装样，分7层分别装样，各层土样质量尽量相同并以同等击实功击实，以保证试样的均匀性。装样过程中通过干密度控制孔隙率的大小，即由式计算得到，其中干密度由试验得到，例如表2中0.10～0.25 mm粒径区间孔隙率与干密度的对应值。试验前自下而上在较低水头下将试样排气饱和，并浸泡12 h左右，排除系统内空气提高试验精度。试验时渗透自上而下，水力坡降按0.010、0.015、0.020、0.025、0.030、0.040……，逐级增加，这种加载方案可以避免水力坡降过大造成土样发生渗透破坏。各级压力加载完毕后，待测压管水头高度不再变化时方可读测。

表2 0.10～0.25 mm粒径细砂孔隙率与干密度控制值Table 2 Values of porosity and dry density of sand with 0.10-0.25 mm particle diameter

3 试验结果及分析

3.1 各粒径级不同孔隙率下土样的渗透试验结果

将各个粒径级土料分别压实到不同的孔隙率，在直角坐标系中绘制渗流速度V与水力坡降J的关系曲线，以描述随着水力梯度的增大流体流动过程的变化，如图2所示，土中V20表示20°C时的渗流速度。不同孔隙率下渗透系数的大小取V-J曲线直线段部分趋势线的斜率值，以此保证所得值为层流状态下的渗透系数，确保达西定律的适用。对不同粒径级的试验结果分别进行线性回归分析，并通过散点图和趋势线表示孔隙率n与20°C时的渗透系数K20之间的相关关系，如图3所示，不同粒径级土料K20与n的线性相关度 R2，列于表3。由表可知，同一粒径级随着孔隙率的逐渐增大，渗透系数也随之增大，渗透系数与孔隙率一次方呈现正相关关系，且二者的线性相关度较高。从微观角度上来看，对于同一粒径级的土料，其颗粒大小相对较为均一，均值粒径可作为土颗粒大小的代表值，随着孔隙率的增大，单位体积土体内所包含的孔隙体积也随之增大，平均孔隙直径增大，土样变得相对松散。孔隙体积的增大使得单位土体在同等的水头压力下流体流经的断面面积相对增大，故单位时间内的渗流量随着孔隙率的增大而变大。

图2 不同孔隙率下粒径为0.10～0.25 mm时V-J曲线Fig.2 V-J curves for different porosities with 0.10-0.25 mm particle diameter

图3 0.10～0.25 mm粒径细砂样渗透系数与孔隙率的相关关系Fig.3 Relationship between permeability coefficient and porosities of sand with 0.10-0.25 mm particle diameter

表3 各粒径级渗透系数与孔隙率的相关关系Table 3 The correlation between permeability coefficient and porosity of each particle size fraction

3.2 同一孔隙率不同粒径级下土样的渗透试验结果

将不同粒径级的土料分别压实到同一孔隙率下进行渗透试验，其结果如表4所示，相关性分析如图4所示。由表可知，同一孔隙率下不同粒径级土料的渗透系数不同，随着粒径区间的增大，渗透系数也逐渐增大，变化大小在一个数量级以上。根据图4可知，各粒径级均值粒径 da的二次方与渗透系数的相关程度极高，二者具有良好的线性正相关性。在孔隙率一定的条件下，同等土体内部所包含的孔隙体积相同，均值粒径的增大使得土颗粒间孔隙尺寸随之增大，总的孔隙体积相同，平均孔隙直径增大，则相应孔隙数量减少。平均孔隙直径的增大，使得流体通过的断面增大；孔隙数量的减少，则使得流体绕流的路程缩短，水头损失降低，单位时间的渗流量增大。

图4 渗透系数与均值粒径的相关关系Fig.4 Relationship between permeability coefficient and average particle diameters

表4 渗透系数与均值粒径的相关数值Table 4 Values of permeability coefficient and average particle diameter

3.3 混合粒径不同级配下的渗透试验结果

单一粒径级中特征粒径以均值粒径表征，其大小趋于一恒定值，孔隙率为渗透系数的惟一影响因素；不同粒径级之间，在孔隙率一定的条件下，均值粒径的差异成为渗透系数的另一惟一影响因素，粒径级层面的研究使得砂土渗透性影响因素更加明确。对于天然砂土，在孔隙率、特征粒径一定的情况下，土体内部各组分颗粒含量并不惟一，颗粒组成存在着一定的变化维度，颗粒组成的变化或多或少的影响着渗透系数。鉴于细颗粒含量对砂土渗透性的本质影响，为了便于研究颗粒组成与渗透性之间的相互关系，以有效粒径 d10作为天然砂土的特征粒径，通过引入颗粒组成相关参数，参照单一粒径级的相关结论，建立新的渗透系数模型。

3.3.1 曲率系数对砂土渗透性的影响

在孔隙率n、有效粒径 d10为常数的情况下同时控制不均匀系数 Cu不变，不均匀系数的恒定限制了颗粒组成中颗粒离散度的变化，曲率系数成为颗粒组成的惟一变量，级配曲线如图5所示，各参数的大小及试验结果见表5、图6。根据图、表可知，随着曲率系数的增大，渗透系数呈增大趋势，且由图6可知，渗透系数与曲率系数具有良好的线性相关性，相关度为0.980。曲率系数是反映土体颗粒组成连续性的一个参量，在有效粒径一定的情况下，曲率系数越大，控制粒径 d60与中间粒径相差越大，甚至出现粒级缺失情况，在级配曲线上表现为出现平台段。曲率系数越大，颗粒组成的连续性越差，粒径的缺失导致大颗粒间的孔隙不能有效填充，致使孔隙体积增大，导致渗透系数的增大。

图5 不同曲率系数下的颗粒级配曲线Fig.5 Grading curves with different curvature coefficients

表5 渗透系数与曲率系数的相关数值Table 5 Values of permeability coefficient and curvature coefficient

3.3.2 不均匀系数对砂土渗透性的影响

在孔隙率n、有效粒径 d10为常量的情况下控制曲率系数恒定，曲率系数的恒定限制了颗粒组成中颗粒连续性好坏这一变化维度，不均匀系数 Cu成为颗粒组成惟一变量，级配曲线如图7所示，各参数的大小及试验结果见表6、图8。根据图、表可知，随着不均匀系数的增大，渗透系数也随之增大。由图8可知，渗透系数与不均匀系数之间存在着较好的线性相关性，其相关度为0.837。不均匀系数是反映土体中土颗粒离散程度的量，不均匀系数越大，其粒径变化范围就越大，反映在颗粒级配曲线上表现为曲线变化平缓。较大不均匀系数的土体，在有效粒径一定的情况下，控制粒径 d60的上限值增大，粗颗粒和细颗粒的大小相差愈悬殊，在孔隙率一定的情况下，粗颗粒之间的孔隙与细颗粒含量不相对等，即孔隙得不到完全的填充，致使土体中孔隙增大，渗透系数增大。

图6 渗透系数与曲率系数的相关关系Fig.6 Relationship between permeability coefficient and curvature coefficient

图7 不同不均匀系数下的颗粒级配曲线Fig.7 Grading curves with different uniformity coefficients

表6 渗透系数与不均匀系数的相关数值Table 6 Values of permeability coefficient and uniformity coefficient

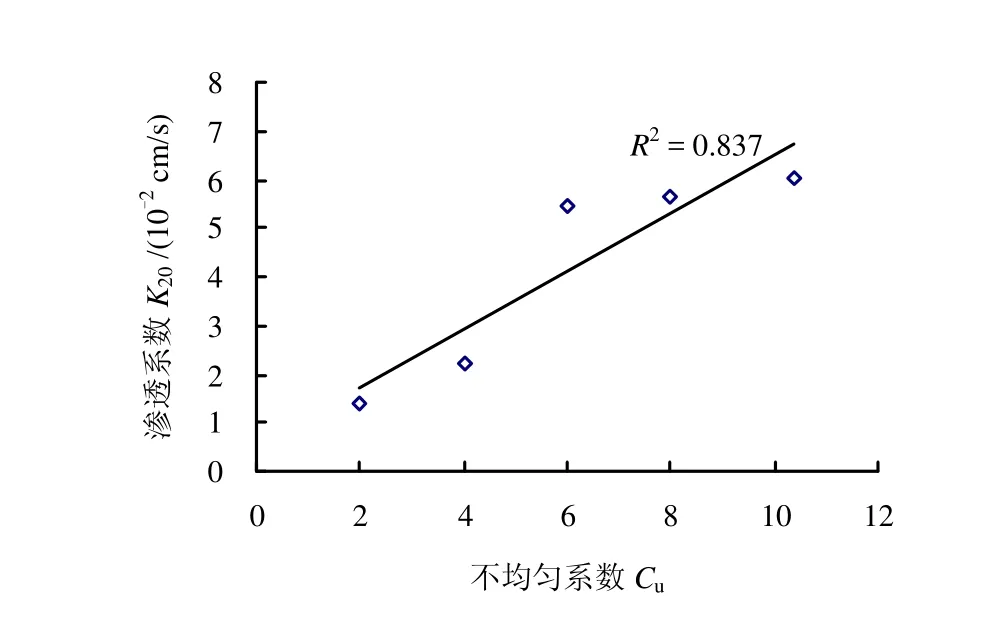
图8 渗透系数与不均匀系数的相关关系Fig.8 Relationship between permeability coefficient and uniformity coefficient

4 经验公式的拟合

根据试验数据，通过相关分析，渗透系数与孔隙率、有效粒径的二次方、曲率系数、不均匀系数有着密切的线性相关关系，且相关程度均较高。通过一定线性回归分析，可将4个参量拟合在同一公式中以表述渗透系数的大小，作为经验公式用于工程实践中预测天然砂土渗透性。其拟合结果如下：

式中：K为渗透系数（cm/s）；C为无因次系数，可取为157。

将本文拟合公式计算值 K、Terzaghi公式计算值KTerzaghi、Hazen公式计算值KHazen、Kozeny公式计算值 KKozeny、扎乌叶布列公式计算值 K18、水科院公式计算值K水科院、朱崇辉公式计算值K朱崇辉与实测值K20的比值列于表7中。

经过比较可知，基于单一粒径级经验公式基础之上经不均匀系数、曲率系数修正得到的公式计算结果与实测值较为接近，相比太沙基公式、哈增公式、柯森公式等精确度得到较大程度的提高，具备作为实际工程中砂性土渗透系数的预测条件，具有较高的实用性。表7中各经验公式渗透系数的计算值各不相同，产生这种差异性主要原因在于研究对象及研究方法的不同，先前关于渗透系数的研究均以天然混合料砂土作为研究对象，诸多研究人员均通过选取合适的粒径来表征整个土体的粒径大小，颗粒复杂组成很少被单独考虑。本文则首先以单一粒径级砂土作为研究对象得出渗透系数与其影响因素的精确线性相关关系，而后引入颗粒组成的影响修正单一粒径级结论，进而综合考虑拟合出天然砂土的渗透系数经验公式。随着 Cu、Cc的增大，表7中预测值与实测值出现一定的偏差，其原因可能在于，随着土体不均匀性的增强、土体连续性的变化，土体内部结构组成形式可变性增强，内部结构性的细微差异导致渗透系数发生变化，基于砂土成因及其内部结构对渗透系数的影响有待进一步从细观上予以研究。

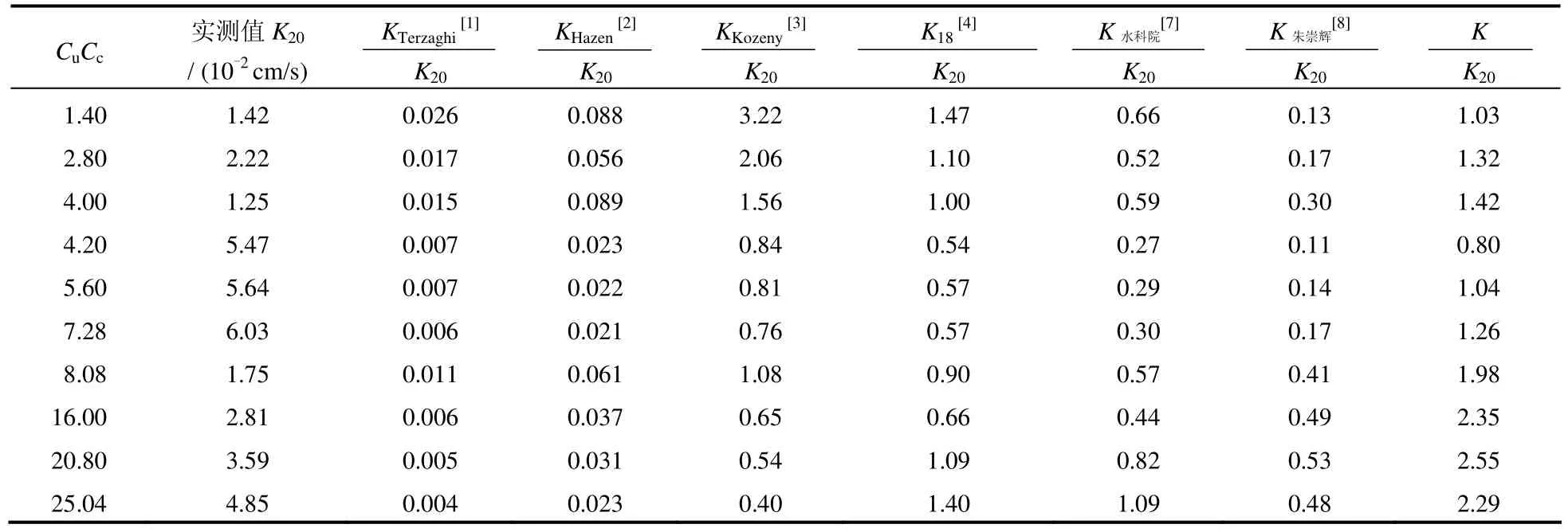
表7 粒径经验公式与实测值的比值Table 7 Ratios of empirical formula of particle diameter and measured value

5 结 论

（1）对于单一粒径级范围的砂土，渗透系数随着孔隙率的增加而线性增加、随均值粒径二次方的增加而线性增加，其中尤以均值粒径对渗透系数的影响较大，均值粒径的变化能导致渗透系数量级上的差异。

（2）对于天然砂土，有效粒径、孔隙率、曲率系数、不均匀系数对渗透系数都有着一定的影响，这4个参数与渗透系数都存在着较好的线性正相关性。

（3）通过线性回归分析，综合4个因素拟合出经验性渗透系数计算公式，可供工程实践中估算天然砂土渗透系数和配制有特定渗透性要求的砂土时使用。

[1]太沙基,帕克.工程实用土力学[M].蒋彭年译.北京:水利电力出版社,1960.

[2]POLLARD W S,POULOS STEVE J,SANGREY DWIGHT A.Air diffusion through membranes in triaxial test[J].Journal of the Geotechnical Engineering Division,1977,103(10): 1169－1173.

[3]米切尔 J K.岩土工程土性分析原理[M].南京: 南京工学院出版社,1988.

[4]刘杰.土石坝渗流控制理论基础及工程经验教训[M].北京: 中国水利水电出版社,2006.

[5]HANSEN DAVID.Discussion of “on the use of the Kozeny–Carman equation to predict the hydraulic conductivity of soils[J].Canadian Geotechnical Journal,2004,41(5): 990－993.

[6]CHAPUIS ROBERT P.Predicting the saturated hydraulic conductivity of sand and gravel using effective diameter and void ratio[J].Canadian Geotechnical Journal,2004,41(5): 787－795.

[7]刘杰.土的渗透稳定与渗流控制[M].北京: 水利电力出版社,1992.

[8]朱崇辉.粗粒土的渗透特性研究[硕士学位论文 D].杨凌: 西北农林科技大学,2006.

[9]杨靖,汪吉林.砂性土渗流的分型特征研究[J].煤田地质与勘探,2010,38(2): 42－45.YANG Jing,WNAG Ji-lin.Research on fractal characteristics of permeability of sandy soil[J].Coal Geology &Exploration,2010,38(2): 42－45.

[10]崔荣芳.无黏性土的渗透特性及其管涌破坏机理研究[硕士学位论文D].南京: 河海大学,2006.

[11]南京水利科学研究院.SL237－1999土工试验规程[S].北京: 中国水利水电出版社,1999.