对两相材料薄板声功率及其灵敏度研究

薛晓理，吴锦武，赵龙胜

(南昌航空大学飞行器工程学院，江西南昌 330063)

0 引 言

环境中存在各种各样的振动现象，振动辐射噪声污染环境，因而受到广泛关注。机器结构声辐射噪声的大小成为评价其动态性能的重要指标。基于声辐射模态研究结构声功率及其灵敏度，对降低噪声有重要的指导意义。声功率灵敏度是指声功率关于设计参数的变化率，能够量化各设计参数对声功率的影响程度，以声功率灵敏度为指标，通过定量修改设计参数，降低结构辐射噪声，是结构优化设计的重要途径。

90年代初，Borgiotti、Cunefare、Elliott[1-3]等学者提出声辐射模态的概念，其实质是将结构表面的振动分解成一组声辐射独立的速度分布，这样声功率可表示成每阶声辐射模态速度幅值的平方与相应特征值乘积的和。近年来，边界元法和有限元法联合求解声辐射问题得到广泛应用[4-6]。Salagame[7]等学者通过瑞利积分推出了声功率灵敏度表达式，姜哲等[8]学者分析了加筋板的声功率灵敏度。

本文进一步拓展求解声功率及其灵敏度的研究范围，基于声辐射模态再结合有限元求解两相材料薄板的声功率及其关于设计参数的灵敏度。建立有限元模型，处理振动环节，用振型叠加法求解模态坐标从而求出结构的速度分布，用声辐射模态方法处理声辐射环节。

1 有限元模型

利用有限元法建立阻尼振动系统在外力激励下的振动微分方程：

其中M、C、K分别为结构质量矩阵、阻尼矩阵、刚度矩阵，F0为激励力幅值向量，ω为激励频率，δ为振动法向位移向量。结构的阻尼一般难以准确确定，工程中常采用Raileigh阻尼，将阻尼矩阵表示成质量矩阵和刚度矩阵的线性组合[9]：

其中α、β为常数，与结构的固有频率和阻尼比有关。设ωi、ωj分别为第i个和第j个固有频率，ξi、ξj分别为第i个和第j个振型的阻尼比(即实际阻尼和改振型的临界阻尼的比值)，则α、β表示为：

设在简谐力激励下结构法向位移响应复数形式为

将式(5)代入式(1)，约去时间项得到：

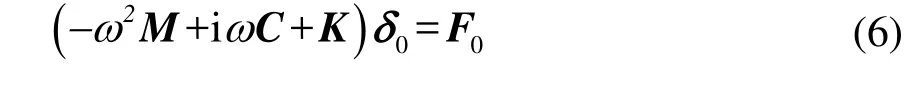
可得到：

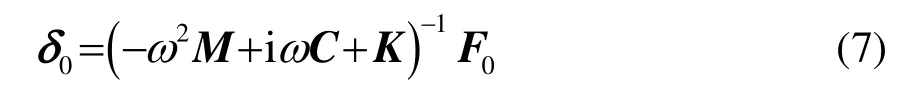
若用式(7)直接求解，则需要矩阵求逆运算，大规模的矩阵逆运算耗时且由于取舍误差导致运算结果误差较大。利用振型叠加法求解模态坐标，从而求得结构的速度分布。

在求出无阻尼振动的固有频率和振型的基础上，将位移向量δ0看成是振型[φ]的线性组合，引入变换式：

ηi称为模态坐标，将式(8)代入式(6)，方程左右两端同时左乘[φ]T，得到：

将对角化后的刚度矩阵、质量矩阵、阻尼矩阵代入式(9)可实现对振动微分方程的解耦：

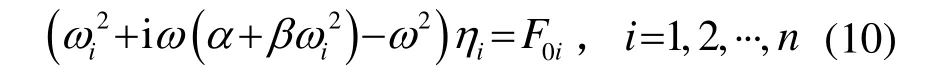
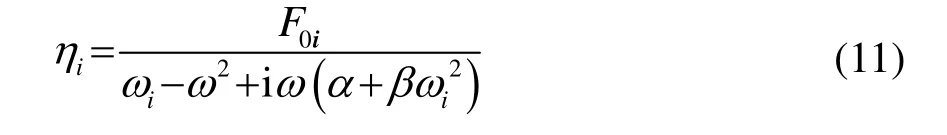
解式(10)得到模态坐标：

对于线性系统的动力响应分析，振型叠加法是很有效的。它的优点在于简便。由于高振型对反应的贡献不显著，通常考虑前几阶振型的反应贡献就可得到所需的精度。

振动法向速度是法向位移关于时间的导数，舍去时间因子项，得到

振速对设计参数x求偏导为：

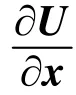
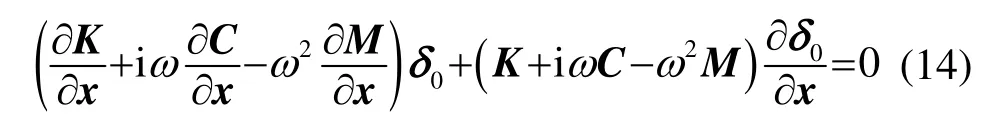
由式(13)、(14)得到：

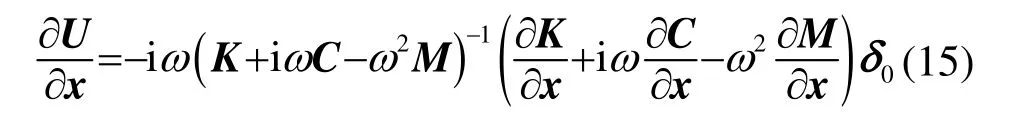
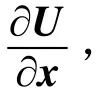
2 声辐射模态模型

任意形状的振动结构表面S以圆频率ω振动，向无界空间V辐射声。在空间V中充满均匀介质，介质的密度为ρ，声速为c。设振动表面S上的法相振速为U，辐射声压为P(ω)。对于单频振动，结构的辐射声功率[10]可表示为：

式中：Re表示取复数实部，上标H表示矩阵共轭转置。

通过瑞利积分，平板上任一点X处声压P(X,ω)与结构表面法相振速可离散为

式中，Z为阻抗矩阵。

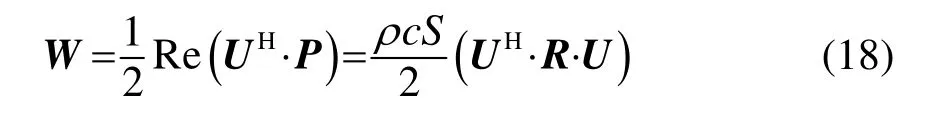
由式(17)，可将式(16)写成如下形式[10]：R为实对称正定矩阵[10]，将其进行特征值分解可以得到一个正交矩阵Q和对角矩阵：Λ

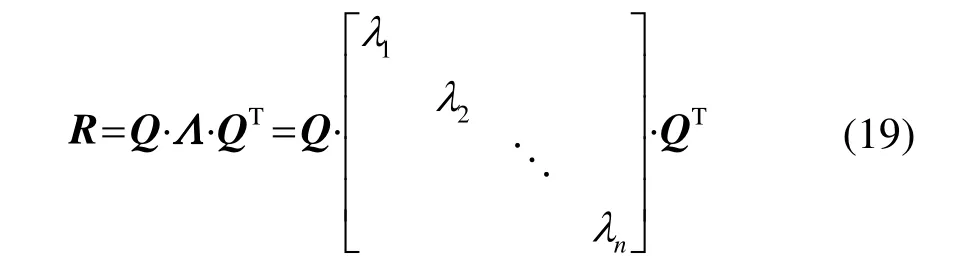
式(19)中，T表示矩阵转置；n为结构离散节点数，Λ为由特征值λi构成的对角矩阵。将式(19)代入式(18)可以得到

式中：y=QH·U，称为声辐射模态的伴随系数矩阵，yi为第i阶声辐射模态伴随系数。根据式(20)，可以得到声功率关于设计参数x的偏导数，即声功率灵敏度为：

特别对于与分析频率无关的参数，由于辐射表面形状、尺寸不受影响，此时声辐射模态不发生变化。声功率灵敏度表达变为

3 算例及分析

3.1 声功率分析

设采用工程中常用的矩形薄板结构，薄板由两相材料构成，一种为刚性材料，一种为柔性材料。

设薄板的长、宽以及厚分别为a=0.2m，b=0.2m，t=0.001m 。给定结构刚性材料(钢)和柔性材料(PVF)弹性模量分别为E1= 2 .1×1011N/m2，密度分别为ρ1=7800 kg/m3，泊松比μ=0.3，空气密度声速c=343m/s。在板中心位置施加单频激励力，幅值F0=1N，激励频率为1:8 00 Hz。

根据 Bendøse[11]的研究结果，得到复合薄板的弹性模量和密度按照带惩罚的变密度SIMP插值方式构成：

式中：x为材料分布密度，取= 0 .5，惩罚因子p=4。

对两相材料薄板进行模态分析，得到了结构的前10阶模态频率见表1。

表1 简支薄板前十阶固有频率Table.1 The first ten natural frequencies of a simple supported plate

根据式(18)得到了薄板随频率变化的声功率级，所得结果如图1所示。

分析表1和图1可知，薄板在第一阶固有频率(72.6 Hz)处声功率达到最大值，在结构设计时应当避免激励频率与第一阶固有频率接近。本例中薄板是正方形，其第(m,n)阶和第(n,m)阶模态频率相等，在第5阶和第6阶的时候，实际激起的模态振型有两阶，因此在这个频率(362.9 Hz)的时候，结构辐射声功率也很大。

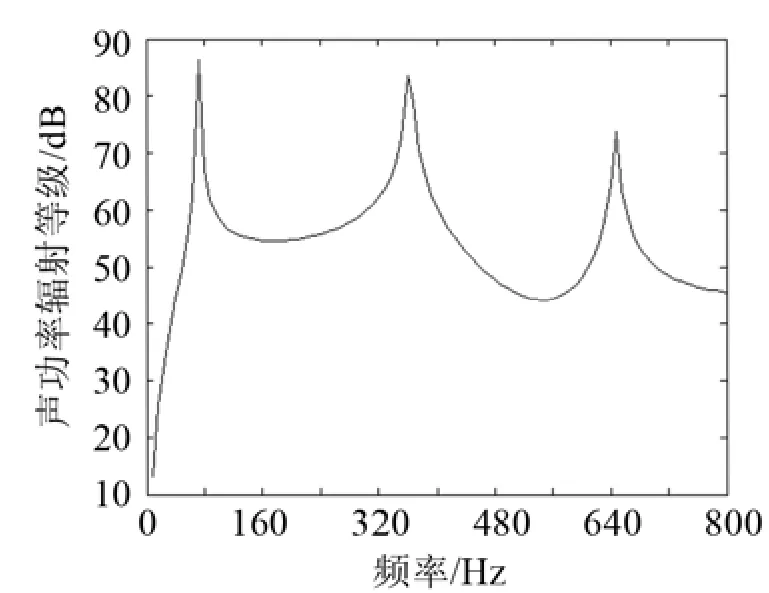
图1 薄板辐射声功率级Fig.1 Sound power level radiated by a thin plate

3.2 声功率关于板厚的灵敏度分析

为了从理论上研究分析两相材料薄板的厚度、分布密度和振动频率对薄板声辐射的影响，在上述模型的基础上，分别改变算例中板厚和分布密度，对其进行研究。

按照算例模型，板的厚度t可变，其变化规律为：t=(0.008+0.008n) mm，(n=0,1,2,…,99)。分析了激励频率为100、200、300、400 Hz时声功率及其关于板厚变化的灵敏度，得到图2和图3。

分析图2、图3可知，当声功率达到峰值时，相应的声功率灵敏度也达到峰值，这些峰值是由于激励频率与薄板的固有频率接近使薄板产生了共振。

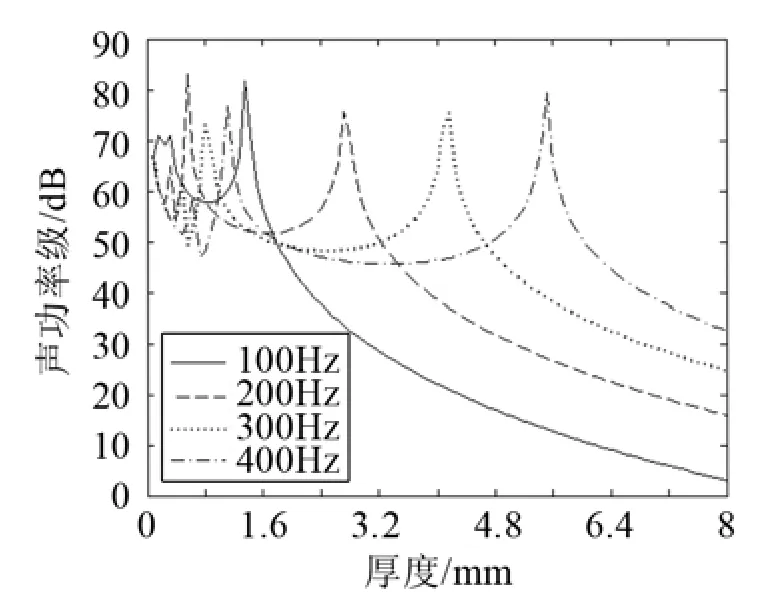
图2 不同厚度下薄板的声辐射功率Fig.2 Sound powers radiated by the plate of different thicknesses

薄板厚度在1 mm以下时，声功率及其灵敏度随着板厚的变化比较明显。随着厚度的增加，声功率及其灵敏度会出现一些“平坦区域”，在这些区域内，板厚对声功率的影响不明显。

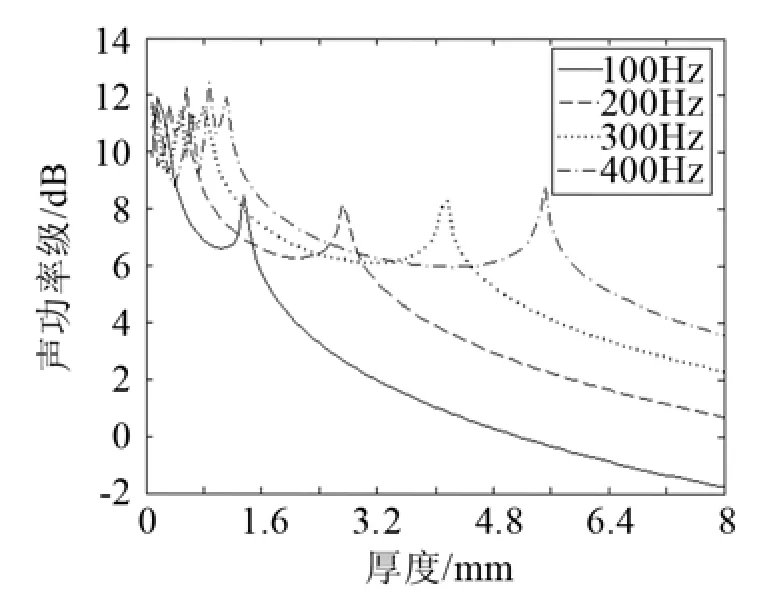
图3 薄板关于厚度的声功率灵敏度Fig.3 Sound power sensitivity to the thickness of the plate

随着激励频率的增大，声功率及其灵敏度的峰值位置所对应的薄板厚度在向后推移。激励频率为100 Hz时，峰值出现在1.36 mm处，声功率及其灵敏度分别为81.606 dB和8.466；200 Hz时，峰值出现在2.72 mm处，声功率及其灵敏度分别为75.548 dB和8.134；300 Hz时，峰值出现在4.16 mm处，声功率及其灵敏度分别为75.326 dB和8.255；400 Hz时，峰值出现在5.52 mm处，声功率及其灵敏度分别为79.312 dB和8.783。说明在实际中不是薄板的厚度越大越好，薄板的厚度应该根据结构的激励源来确定。

3.3 声功率关于分布密度的灵敏度分析

按照算例模型，板的材料密度分布x可变，其变化规律为：x=0.01+0.01n，(n=1,2,…,99)。分析了激励频率为100、200、300、400 Hz时声功率及其关于分布密度变化的灵敏度，得到图4和图5。

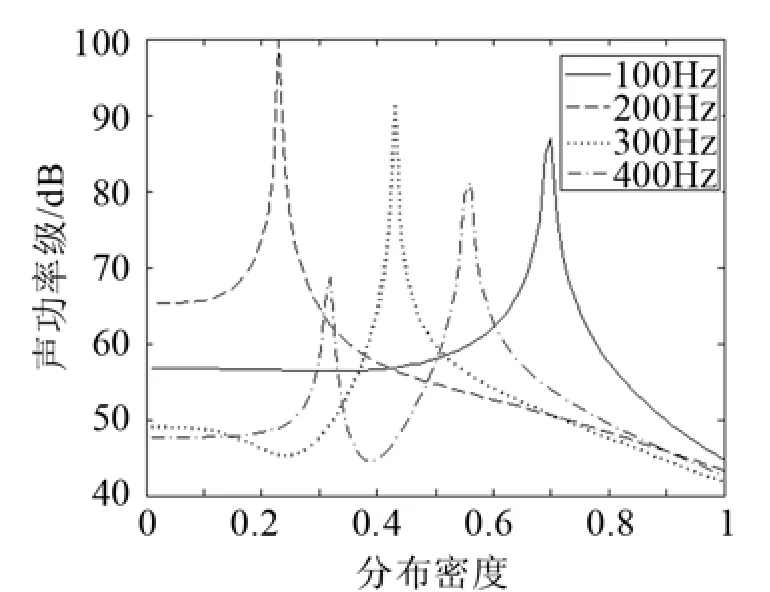
图4 不同分布密度下的薄板声功率Fig.4 Sound power radiated by the plate of different distribution densities

分析图4、5可知，当声功率达到峰值时，相应的声功率灵敏度也达到峰值，这些峰值是由于薄板在激励频率下产生了共振。在峰值之前，声功率及其灵敏度出现了“平坦区域”，在这区域内调整结构的材料分布密度，不能有效地控制结构噪声。在峰值之后，薄板声功率随密度的增大而迅速减小。

图5 薄板关于分布密度的声功率灵敏度Fig.5 Sound power sensitivity to the distribution density of the plate

在低频激励时，声功率及其灵敏度出现峰值次数很少，随着激励频率的增加，声功率及其灵敏度出现峰值的次数也在增加，变化也越来越复杂。

3.4 声功率综合分析

分别取图2和图4峰值位置的板厚与分布密度，在相应的激励频率下求得相应的声功率，得到表2。表2中的声功率明显小于图2和图4中峰值位置所对应的声功率，说明两相材料薄板的声功率受到薄板厚度、材料分布密度、外界激励频率的综合因素的影响。

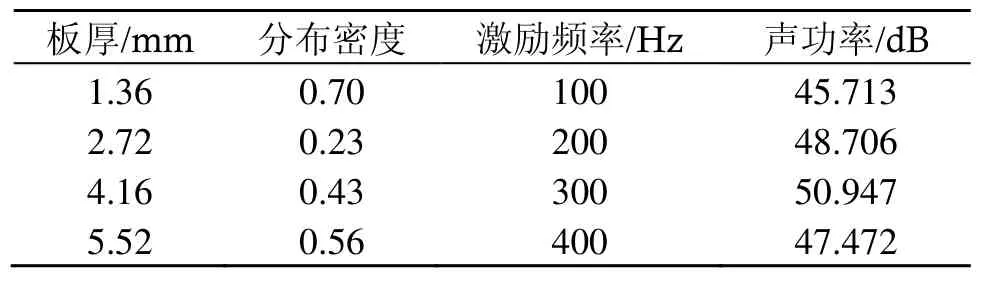
表2 简支薄板声功率Table 2 Sound power radiated by a simple supported plate

综合分析得到：当激励频率接近薄板固有频率附近，结构声辐射功率急剧增加达到峰值。在“平坦区域”内，薄板的声辐射功率并不随着板厚与密度分布的增加而减小，这主要是由于薄板的固有频率随着板厚与分布密度的变化而变化，从而引起声辐射功率的变化。同时可以看出，随着结构厚度或者分布密度的增加，结构辐射声功率的总体变化趋势是减小的，但声辐射功率并不是随结构厚度或者分布密度的增加而单调减小，在某些厚度或者分布密度下，结构辐射声功率不降反升。同时也说明，薄板结构并不是越厚越好，也不是密度越大越好，其厚度与分布密度值的选择还应取决于激励源特性。

4 结 论

本文利用有限元与声辐射模态对两相材料薄板结构的声辐射声功率及其关于设计参数的灵敏度进行了研究，以四边简支正方形薄板为例，分析了激励频率、薄板厚度与分布密度的变化对其声辐射的影响。在有限元部分，用振型叠加法求解模态坐标得到位移向量，从而得到薄板表面速度分布。基于声辐射模态理论，求解了声功率及其关于设计参数的灵敏度。

数值计算结果表明：对于动力响应分析，振型叠加法是很有效的。激励频率、不同的板厚与分布密度对薄板的声辐射都有较大的影响。

将有限元与声辐射模态方法相结合，可以实现对任意边界条件薄板的声辐射特性进行研究，从而为低噪声设计提供理论依据，对实际中结构的设计有重要的指导意义。

参考文献

[1] Giorgio V Borgiotti. The power radiated by a vibrating body in an acoustic fluid and its determination from boundary measurements[J]. J. Acoust. Soc. Am, 1990, 88(4): 1884-1893.

[2] Cunefare K A, Koopmann G H. Acoustic design sensitivity for structural radiators [J]. ASME, J. Vib. Acoust, 1992, 114(2):178-186.

[3] Elliott S J, Johnson M E. Radiation modes and the active control of sound power[J]. J. Acoust. Soc. Am, 1993, 94(4): 2194-2204.

[4] 张军, 兆文忠, 张维英. 结构声辐射有限元/边界元法声学-结构灵敏度研究[J]. 振动工程学报, 2005, 18(3): 366-370.ZHANG Jun, ZHAO Wenzhong, ZHANG Weiying. Research on acoustic-structure sensitivity basing on FEM and BEM[J]. Journal of Vibration Engineering, 2005, 18(3): 366-370.

[5] 白杨, 汪鸿振. 声学-结构设计灵敏度分析[J]. 振动与冲击, 2003,22(3): 43-46.BAI Yang, WANG Hongzhen. Acoustic-Structural design sensitivity analysis[J]. Journal of Vibration and Shock, 2003, 22(3): 43-46.

[6] 陈剑, 程昊, 高煜, 等. 基于有限元—边界元的声学构形灵敏度分析[J]. 振动工程学报, 2009, 22(2): 213-217.CHEN Jian, CHENG Hao, GAO Yu, et al. Acoustic configuration sensitivity analysis based on FEM and BEM[J]. Journal of Vibration Engineering, 2009, 22(2): 213-217.

[7] Salagame R R, Koopmann G H. Analytical sensitivity of acoustic power radiated from plates[J]. J. Vib. Acoust, 1995, 117(1): 43-45.

[8] 邱亮, 姜哲, 袁国清. 基于声辐射模态的粘弹性阻尼板声功率灵敏度[J]. 噪声与振动控制, 2009, 5(5): 131-135.QIU Liang, JIANG Zhe, YUAN Guoqing. Analysis of sound power sensitivity of viscoelastic damping plates based on acoustic radiation modes[J]. Noise and Vibration Control, 2009, 5(5):131-135.

[9] 王元汉, 李丽娟, 李银平. 有限元法基础与程序设计[M]. 广州:华南理工大学出版社, 2001: 157.WANG Yuanhan, LI Lijuan, LI Yinping. Finite element theory and programming[M]. Guangzhou: South China University of Technology Press, 2001: 157.

[10] 姜哲. 声辐射问题中模态分析: I理论[J]. 声学学报, 2004, 29(6):507-515.JIANG Zhe. A modal analysis for the acoustic radiation problems:I Theory[J]. Acta Acustica, 2004, 29(6): 507-515.

[11] Bendøse M P, Sigmund O. Material interpolation schemes topology optimization[J]. Arch Appl Mech, 1999, 69(9-10): 635-654.