基于线性规划的通信保障专业队配置方法研究

李勇

国防信息学院 信息化建设系，湖北 武汉 430010

基于线性规划的通信保障专业队配置方法研究

李勇

国防信息学院 信息化建设系，湖北 武汉 430010

合理优化配置通信保障专业队对于提高通信保障能力十分重要。分析了通信保障专业队的实际需求和基本原则，利用线性规划理论对通信保障专业队配置中的部署点选址和力量分配进行了研究，建立了通信保障专业队部署点选址模型和力量分配模型，并对模型算法进行了分析。选址模型和力量分配模型可快速生成部署点选址和力量分配矩阵，辅助制定相关方案。

线性规划；配置；P-中值模型；选址

通信保障专业队配置是指在现有通信网络条件下，研究部署通信保障专业队伍，并合理配置通信保障专业队力量，以期在出现突发紧急事件，能及时调度通信保障专业队伍，最大限度地保障通信网络的连通性能。合理优化配置通信保障专业队对于提高通信保障能力具有十分重要的意义，利用线性规划理论可以辅助制定通信保障专业队配置方案。

1 通信保障专业队配置需求与流程

1.1 配置需求

通信保障专业队配置的主要任务是确定各分队的部署位置、各部署点承担的保障任务以及各分队对应于部署点的力量分配。由于通信保障所涉及的因素较为复杂，因此目前对于通信保障专业队的配置，普遍按照隶属原则和就近分配原则进行配置和部署。

1.2 配置流程

通信保障专业队的配置通常是依据平时制定的通信保障预案开展和实施的。配置基本步骤如下：首先分析通信网络结构，根据对通信设施的毁伤概率和网络连通性的分析，评价通信网络中各节点和链路的重要性指标；然后分析各通信设施的位置分布，结合其重要性指标，选择专业队部署点；最后按照有关的配置原则和现有通信保障力量情况，为各部署点分配专业队力量。通信保障专业队配置基本流程如图1所示。

图1 通信保障专业队配置基本流程

1.2.1 通信设施重要性评估

在通信保障专业队配置的影响因素中，最为重要的是各通信设施的重要性程度。因此，通信保障专业队配置首先就需要分析通信网络结构，根据对现有通信设施的毁伤概率和网络连通性的分析，评价通信网络中各节点和链路的重要性指标。

1.2.2 通信保障专业队部署点选址

通信保障专业队部署点是指各通信保障专业分队按照预先制订的通信保障预案部署待命的位置，一般是从现有的重要通信设施所在位置中选择。通信保障专业队部署点选择就是根据实际情况，合理配置部署点，在充分满足通信保障任务的前提下尽可能减少各分队从部署点到达需要保障的任务位置所消耗的时间。

1.2.3 通信保障专业队力量分配

通信保障专业队力量分配是指根据确定的专业队部署点所承担的通信保障任务以及现有的通信保障力量，为各个部署点分配相应的通信保障专业分队，以最大限度地满足各个部署点所承担的通信保障任务。

2 通信保障专业队配置模型与算法

2.1 部署点选址模型与算法

2.1.1 选址模型

根据P-中值模型，建立通信保障专业队部署点选址数学模型：在给定数量和位置的通信设施集合以及距离阈值条件下，从候选位置集合（所有通信设施所在位置的集合）中，选择若干个专业队部署点位置并指派每个部署点负责若干个通信设施的保障任务，使之达到从所有专业队部署点位置到相应负责抢修的通信设施所在位置的距离最短且小于指定的阈值。

其目标函数是：

maxi∈N,j∈M(yijdij)≤T式中：N为n个通信设施，M为m个候选的专业队部署点位置，yij为专业队部署点任务分配变量，其取值为：

yij={0， 1},i∈N，j∈M。当候选的专业队部署点j承担通信设施i的保障任务时，yij=1，否则，yij=0；dij为从通信设施i所在位置到专业队部署点位置j的路程，T为指定的距离阈值。

其约束条件为：

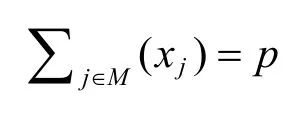
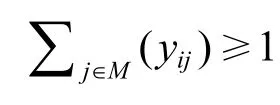
2.1.2 模型算法

该模型可采用贪婪取走启发式算法进行求解。在介绍算法之前，先引入几个要素：

通信设施重要性指标数组A=[ai]m。其中，ai∈(0， 1)，表示通信设施i的重要性指标。

任务分配矩阵Y=[yij]m×m。其中，yij∈{0， 1}，若yij=1，表示候选专业队部署点j承担通信设施i的保障任务。依照以下的规则初始化任务分配矩阵Y=[yij]m×m：矩阵对角线元素全部定义为1，即yii=1，(i=1,2,…,m)；其余元素定义为：yij=0；通过计算以后的任务分配矩阵Y即为最终模型计算所求的结果。

距离矩阵D=[dij]m×m。式中dij表示通信设施i到通信设施j的距离。

模型求解算法步骤如下，算法流程如图2所示。

图2 通信保障专业队部署点选址算法流程

1）建立节点重要性指标矩阵A，重要性指标取值范围为（0，1）；

2）选择现有的所有通信节点设施所在位置为候选位置，共有m个候选位置，每个通信节点指派其对应的候选位置承担保障任务，初始化任务分配矩阵Y；

3）确定距离阈值T，建立距离矩阵D；

4）在A中从小到大依次选择并取走一个候选专业队部署点位置，计算目标函数，假如将其取走并将它对应的通信节点设施重新指派后，目标函数仍然成立，且在其中距离增加量最小，根据新的任务分配情况修改Y，然后令p=p-1，进行下一步；假如将其取走并将它对应的通信设施重新指派后，总的距离增加量为最小，但目标函数不成立，退出循环，当前任务分配矩阵Y即为所求；

5）返回2），继续运行，直到p=0，结束。

2.2 力量分配模型与算法

2.2.1 力量分配模型

通信保障专业队力量分配是指根据确定的专业队部署点所承担的通信保障任务以及现有的通信保障力量情况，为各个部署点分配相应的保障专业分队，以最大限度地满足各个部署点所承担的通信保障任务。

其数学模型如下：在给定数量和类型的通信保障专业队集合以及给定数量的专业队部署点（其通信保障任务已确定）集合的条件下，合理分配专业队力量，使得专业队部署点内的保障人员数量与所承担的保障任务数量比例之均方差最小或保障能力与所承担的保障任务难度比例之均方差最小。

其目标函数可根据实际需要选择以下函数之一：

1）目标函数只考虑专业队部署点内的保障人员数量与所承担的保障任务数量

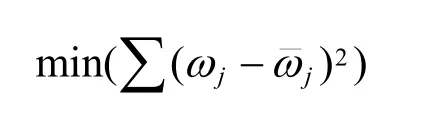
2）目标函数只考虑专业队部署点内的保障能力与所承担的保障任务难度

3）目标函数综合考虑专业队部署点内的保障人员数量与所承担的保障任务以及保障能力与所承担的保障任务难度

式中：π1为保障数量权重，π2为保障能力权重。

jω为第j个专业队部署点内专业队保障人员数量与所承担的保障任务数量之比，其计算公式为

式中：M为m个通信保障专业分队，N为n个通信保障专业队部署点，L为l个通信设施，ui表示第i个通信保障专业分队的人员数量。

ω为所有专业队部署点内保障人员的数量与所承担的保障任务数量之比的平均值，其计算公式为

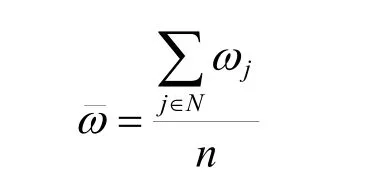
ρj为第j个专业队部署点内的通信保障专业分队保障能力与所承担的保障任务难度之比，其计算公式为

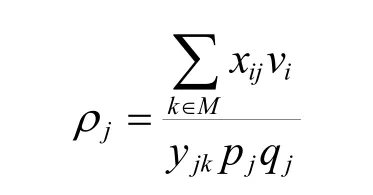
式中M为m个通信保障专业分队，L为l个通信设施，vi表示第i个通信保障专业分队的保障能力指标，pi表示第i个通信设施的重要性指标，qi表示第i个通信设施的保障难度指标。

ρ为所有专业队部署点内保障能力与所承担的保障任务难度之比的平均值，其计算公式为

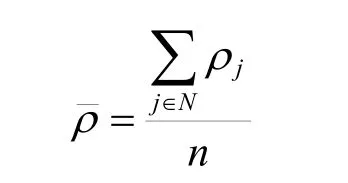
其约束条件为：

xij={0,1},i∈M, j∈N，当专业分队i分配到专业队部署点j时，xij=1；否则，xij=0。

2.2.2 模型算法

对于上述模型，可以采用遍历算法进行求解。在介绍算法之前，先引入以下几个要素：

专业队部署点任务分配矩阵Y=[yjk]n×l。其中，yjk∈{0， 1}，若yjk=1，表示专业队部署点j承担通信设施k的抢修任务；若yjk=0，表示专业队部署点j不承担通信设施k的抢修任务。

专业队力量分配矩阵X=[xij]m×n。式中xij∈{0， 1}，若xij=1，表示通信保障专业分队i被分配到专业队部署点j；若xij=0，表示通信保障专业分队i没有被分配到专业队部署点j。

通信保障专业分队人员数量数组U=[ui]m。其中ui表示通信保障专业分队i的人员数量。

通信保障专业分队保障能力数组V=[vi]m。其中vi∈(0,1)，表示通信保障专业分队i的保障能力指标；

通信设施重要性指标数组P=[pi]l。其中pi∈(0,1)表示通信设施i的重要性指标。

通信设施保障难度指标数组Q=[qi]l。其中qi∈(0,1)表示通信设施i的保障难度指标。

模型求解算法步骤如下：

1）建立专业队部署点任务分配矩阵Y、专业队部署点承担任务数量数组T、通信保障专业分队人员数量数组U、通信保障专业分队保障能力数组V、通信设施重要性指标数组P、通信设施保障难度指标数组Q，初始化专业队力量分配矩阵X；

2）逐列调整专业队力量分配矩阵X内的要素值，计算目标函数，选择目标函数值最大的专业队力量分配矩阵X；

3）重复2），直到按行全部调整完毕，结束。

3 实例分析

运用文中提出的通信保障力量配置模型和算法，分析某市应急通信保障专业队的方法与流程。首先通过网络节点分析建立需要通信节点重要性指标和通信节点保障难度指标（表1所示），确定专业队保障能力指标（表2所示）和通信节点距离矩阵。

表1 通信节点重要性与保障难度指标

表2 专业队保障能力指标

通信节点距离矩阵为

根据专业队部署点选址模型算法可得出任务分配矩阵：

从矩阵中可以得出：分别在1、5、7、9、11共5个通信设施位置附近设置专业队部署点，依次将其编为1、2、3、4、5号专业队部署点，其中1号专业队部署点负责1、2、3号通信设施的抢修任务，2号专业队部署点负责3、4、5、6号通信设施的抢修任务，3号专业队部署点负责6、7、8号通信设施的抢修任务，4号专业队部署点负责8、9、10号通信设施的抢修任务，5号专业队部署点负责11、12号通信设施的抢修任务。

通过专业队力量分配模型算法得出专业队力量分配矩阵：

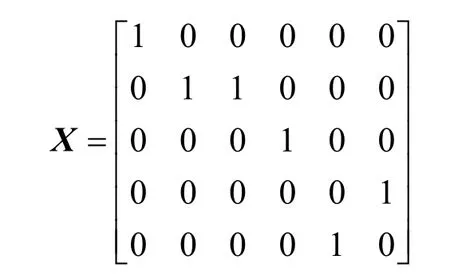
从矩阵中可以得出：1号专业分队被分配到1号专业队部署点，2、3号专业分队被分配到2号专业队部署点，4号专业分队被分配到3号专业队部署点，5号专业分队被分配到5号专业队部署点，6号专业分队被分配到4号专业队部署点。

4 结束语

运用线性规划理论，建立通信保障专业队的部署点选址模型和力量分配模型，可以辅助快速制定科学合理的通信保障任务分配和通信保障力量分配方案，使通信保障方案能最大限度地满足任务需求，提高通信抢修能力。

[1] 李长生. 军事运筹学教程[M]. 北京: 军事科学出版社, 2006: 62-136.

[2] 袁亚湘, 孙文瑜. 最优化理论与方法[M]. 北京: 科学出版社, 2001: 55-731.

[3] 解可新, 韩立兴. 最优化方法[M]. 天津: 天津大学出版社, 2001: 38-42.

[4] 高培旺. 高效求解整数线性规划问题的分支算法[J]. 计算机应用, 2010, 30(4): 1019-1021.

[5] 范国兵. 投资决策的线性规划模型及其应用[J]. 科技与产业, 2010, 10(8): 62-64.

[6] 刘磊. 求解线性规划模型算法的实现研究[J]. 电脑知识与技术, 2010, 6(28): 8146-8148.

[7] 郑国用. 反恐兵力分配运筹方法辅助决策研究[J]. 武警学院学报, 2008(4): 94-96.

[8] 卢厚清. 基于连续覆盖的城市消防站布局优化[J]. 计算机应用, 2012(3): 852-855.

[9] 花文健, 李炳杰. 应急机动通信兵力派遣问题的通用模型[J]. 空军工程大学学报: 自然科学版, 2003(8): 38-40.

[10] STUTZLE T, DORIGO M. A short convergence proof for a class of ant colony optimization algorithm[J]. IEEE Trans on Evolutionary Computation, 2002, 40(6): 458-365.

Research on configuration of communication guarantee special team based on linear programming theory

LI Yong

Department of Informatization Construction, PLA Academy of National Defense Information, Wuhan 430010, China

It is an important question to optimize and configure communication safeguard special team for advancing military communication safeguard ability. Effective requirement and elementary principle for configuring communication safeguard special team were analyzed, and choice for locating position and distribution for safeguard power were researched by making use of the linear programming theory. As a result, location and distribution models for safeguard power were established, and the algorithm of the models was analyzed. The model and algorithm proposed in this paper may be used to rapidly locate position and generate matrix of safeguard power allocation, and help formulate relevant schemes.

linear programming; configuration; p-median model; position-choice

O212.6

A

1009-671X（2014）01-0054-05

10.3969/j.issn.1009-671X.201301014

2013-01-15.

李勇（1978-）, 男, 讲师, 博士.

李勇, E-mail: liyongceyua@163.com.