利用双行根数计算太阳相位角的精度评估

李荣旺，李语强，周 钰

(中国科学院云南天文台，云南 昆明 650011)

利用双行根数计算太阳相位角的精度评估

李荣旺，李语强，周 钰

(中国科学院云南天文台，云南 昆明 650011)

光度特性测量是获取空间目标的物理特性的重要技术手段之一，无论是光变曲线的事后分析还是建立光度变化的仿真模型，都离不开一个重要的参数——太阳相位角(太阳－空间目标－测站的空间夹角)。目前空间目标的位置通常是通过双行根数(TLE)外推获得，存在一定误差，且随外推时间的延长而变大，因而有必要对其计算所得的太阳相位角的精度进行评估。以典型的不同高度的激光测距卫星LAGEOS1、AJISAI、STELLA为研究对象，以全球激光测距资料解算所得的高精度轨道作为参考轨道，对2012年全年利用双行根数计算所得的太阳相位角数据进行了比对分析，结果表明对于LAGEOS1、AJISAI这样的中高轨卫星，由于轨道较高，表征阻力的B恒定，计算所得的太阳相位角偏差较小，角分量级，且随外推时间的延长不会导致偏差明显增大；而对于STELLA这样的低轨卫星，因轨道较低、受变化的大气的影响显著，计算所得的太阳相位角偏差较大，尤其是当B比较大、变化较快时，偏差显著变大，且随外推时间的延长显著增大，在最差情况下:外推1 d约为13′，外推3 d约为50′，外推7 d约为251′，已超出目前的精度要求。因此，在事后分析中应尽可能使用1 d之内的TLE计算太阳相位角，对于B较大且变化较快情况尤其需要注意。另外，针对UTC闰秒的情况，提出了一种处理方法，即在双行根数外推时判断外推时段是否跨越了闰秒时刻，若跨越了则进行修正:增加或减少1 s，相应地需要修改结果对应的时间戳计算方法。

太阳相位角；光度测量；精度评估；双行根数；卫星激光测距

CN53－1189/P ISSN1672－7673

光度特性测量已成为获取空间目标特性的重要技术手段之一，研究方法主要分为以下两类:一是从观测资料出发进行光变曲线的事后分析[1]，二是从物理模型出发建立光度变化模型[2]，两种方法都涉及一个重要的参数——太阳相位角。双行根数定义为:以目标为中心，太阳方向与测站方向之间的夹角。诚然，其精度由目标、太阳、测站三者的几何位置精度决定。

太阳的位置可通过JPL DE405精密星历插值计算获得，由于太阳距离较远，可近似为平行光，其位置误差对相位角的影响较小；观测站的坐标可通过大地测量、卫星观测数据解算等方式获得，一般在大地测量坐标系中给出，亦相对比较精确。

至于目标的位置，北美防空司令部提供的双行根数(TLE)因公开发布、持续更新、已编目目标最完备而被广泛应用，通常通过其外推获得指定时刻的目标位置，双行根数误差相对较大且随外推时间的延长而变大，位置误差基本在百米级以上[3－4]，是相位角误差的主要来源。

考虑到激光测距卫星可通过全球联测资料解算获得厘米级高精度星历，将其作为目标的参考位置计算相位角，对利用双行根数计算所得的相位角进行精度评估。

1 太阳相位角计算方法

根据相位角的定义可得计算公式为:

式中，ρ表示目标在站心坐标系中的位置矢量；ρ☉表示太阳在站心坐标系中的位置矢量，如图1。

测站坐标是在地固系中给出的，因此将目标和太阳的位置统一转换到地固系中再进行相位角的计算。

图1 太阳相位角的定义Fig.1 Illustration of the definition of the solar phase angle

1.1 目标在地固系中的位置计算

双行根数通过特定方法移除了周期变化得到平根数，使用时必须配合相适应的SGP4/SDP4模型精确地重建移除的周期变化部分[5－6]，从而获得较好的预报结果。

双行根数本身对时间系统和坐标系统并没有严格要求，也找不到其严格的定义，但当外推预报使用时需要使用一致的时间系统和坐标系统。

1.1.1 坐标系统及其转换

坐标系统普遍接受的是地心真赤道平春分点(True Equator Mean Equinox，TEME)，特别需要说明的是平春分点存在“历元平春分点(of-epoch)”和“瞬时平春分点(of-date)”之分，其间差别为赤经岁差。

记TEME-of-date坐标系中的位置矢量为rTEME，准地固系中的位置矢量为rPEF，则其间的转换关系如下:

式中，θ称为地球自转角；JDUT1表示用UT1计算所得儒略日时间；JDTT表示用动力学时TT计算所得的儒略日时间。

文[8－9]中给出了采用历元平春分点(of-epoch)时的转换公式，记TEME-of-epoch坐标系中的位置矢量为r′TEME，有:

其中，μ表示赤经岁差，根据IERS 2003规范计算[7]:

1.1.2 时间系统及UTC闰秒的处理

最新的SGP4/SDP4模型是文[6]给出的修正版，时间系统采用UTC，但需要注意的是UTC时系统存在闰秒情况，在外推时段跨越了闰秒时刻的情况下需要进行修正。在该文中指出需要对UTC闰秒引起注意，但并未给出具体的处理方法。其对时间的处理方式如下:输入时刻(Yt＋Dt)、TLE历元时刻(Yepoch＋Depoch)均为UTC时间，以年份和年积日的形式给出，以从TLE历元时刻起算的时长t作为时间变量进行外推计算，外推时长的计算公式如下:

本文提出如下闰秒处理方法:检测外推时段是否跨越了闰秒时刻，若跨越了则根据闰秒情况进行修正。检测判据如下:判定外推时刻的累计闰秒与双行根数历元时刻的累计闰秒是否一致，若不一致，表明该外推时段跨越了闰秒时刻。外推时长的修正公式如下:

其中，ΔAT(T)表示UTC时刻T对应的累计闰秒①http://hpiers.obspm.fr/eoppc/bul/bulc/UTC-TAI.history，可通过查表获得，计算量非常小。

计算结果对应的时间戳亦需要做修正，不能再简单通过双行根数历元时刻累加外推时长计算，因为此时UTC时统已经不是均匀的时统了，需借助均匀时统进行转换。比较直接的方法为借助TT时间，先将双行根数历元时刻由UTC转换为TT，与修正后的外推时长t′累加获得计算结果对应的TT时刻，然后再转换为UTC获得计算结果对应的UTC时间戳。

当然，闰秒情况毕竟比较少，最近一次闰秒为2012年7月1日，累计闰秒为35 s，由闰秒历史可见，从1972年至2014仅有35个闰秒时刻，在日常使用中加入此修正似乎不是特别必要，但对于跨越闰秒时刻的情况下，修正是必不可少的。

1.2 太阳在地固系中的位置计算

太阳位置通过精密星历JPL DE405插值计算获得，其时间系统是一个特定的坐标时Teph，一般使用时可采用动力学时TT代替[10]；坐标系统为ICRS，与J2000历元平赤道坐标系存在如下的转换关系[11]:

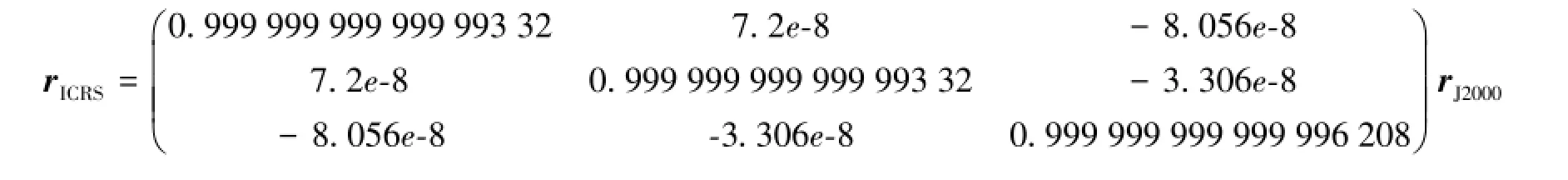
然后再从J2000历元平赤道坐标系转换到地固系中[8]，采用IERS2003规范给出的IAU2000岁差章动模型计算岁差和章动[7]，从而获得太阳在地固系中的位置矢量。

2 精度评估方法

为了评估上述利用双行根数计算所得相位角的精度，需要获取相位角的真实值，或者精度更高的参考值，而目标的位置误差是最主要的误差源。考虑到激光测距卫星具有高精度的全球联测数据，定轨精度可达厘米量级，即目标的位置误差可达厘米级。因此可利用激光测距卫星的精密定轨所得的高精度星历作为目标的参考位置计算相位角，以此作为相位角的参考值进行精度评估。

挑选不同高度的激光测距卫星LAGEOS-1、AJISAI、STELLA为对象，相关参数见表1。

运用云南天文台于2009年研发完成的精密定轨软件系统[12](POREDY)对全球激光测距资料[13]进行精密定轨处理，考虑的力源模型如表2。使用了2012年全年的观测数据，3 d为一个子弧，所得的精密定轨中误差(RMS)如图2。由图可见，LAGEOS 1卫星的位置中误差在2.5 cm左右，AJISAI卫星的位置中误差在3.5 cm左右，STELLA卫星的位置中误差在4 cm左右。

在精密定轨的过程中，同时生成间隔为1 min的星历文件，作为参考位置。

表1 激光测距卫星的相关参数②http://ilrs.gsfc.nasa.gov/missions/satellite＿missions/current＿missions/index.htmlTable 1 The parameters of the SLR satellites

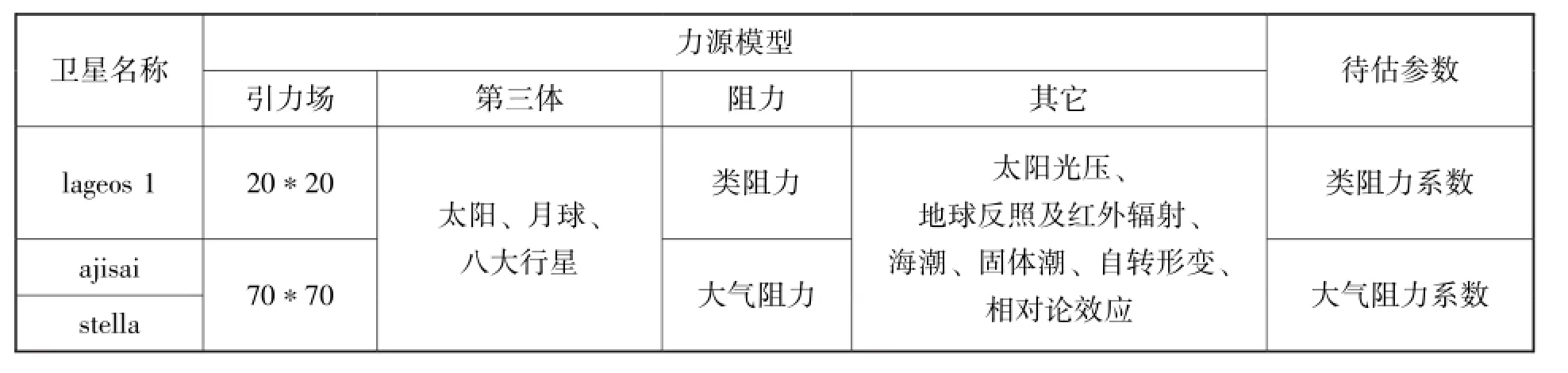
表2 精密定轨软件POREDY中使用的力源模型Table 2 The models of forces from various sources used in the POREDY software package

图2 精密定轨结果的中误差Fig.2 The rms values of results of precision orbit determination using the POREDY package

从space-track网站下载2012年全年的双行根数:LAGEOS 1卫星总计427个、AJISAI卫星总计577个、STELLA卫星总计531个，可见根数一天至少更新一次，但实际使用中存在滞后发布的现象，比如18日的根数可能19日，甚至20日才发布。

观测站设定为昆明站，其大地坐标为:东经102.797 49°、北纬25.030 05°、海拔1 991.0 m，处理流程如下:

(1)以双行根数的历元时刻为基准，外推计算7 d，生成相应的整分钟的位置矢量；

(2)与精密定轨生成的星历进行比对，利用这两种方式获得的位置矢量分别计算对应的相位角并进行比对；

(3)以“空间目标被太阳照亮、处于测站地平高度20°以上”为条件对结果进行筛选；

(4)将筛选的比对结果按1 d、3 d、7 d的外推时长分别进行统计，包括位置偏差的平均值、相位角偏差(绝对值)的最大值，以评估最差情况。

相位角偏差通过下式计算:

式中，φTLE表示利用双行根数计算所得的相位角；φPOD表示利用精密定轨获得的精密星历计算所得的相位角。

3 精度评估结果

3.1 两种TEME坐标系的计算结果

随机选择LAGEOS 1卫星的2012年7月20日的双行根数外推1 d，两种TEME坐标系分别计算所得的相位角偏差如图3，可见采用TEME-of-date计算所得的相位角偏差明显较小，因此TEME采用“瞬时平春分点(of-date)”是比较合适。文[6]指出研究人员普遍相信“of-date”应该是正确的，但并未得到官方的确认，也有人认为“of-epoch”是正确的。与“heavens-above.com”和“www.calsky.com”比对后亦发现采用“瞬时平春分点(of-date)”比较合适。后续的计算将统一采用TEME-of-date坐标系。

3.2 UTC闰秒的处理结果示例

2012年7月1日0时(对应MJD为51609)进行了UTC闰秒③http://datacenter.iers.org/eop/-/somos/5Rgv/document/tx13iers.8q2/bulletinc-043.txt，累计闰秒由34 s增加到35 s。挑选LAGEOS 1卫星的2012年6月31日的双行根数外推1 d，闰秒修正后(外推时长增加1 s)和未修正的相位角偏差如图4，修正前和修正后相位角偏差的最大值分别为2.60′、0.26′，可见未做闰秒修正将引起极大误差，闰秒修正是必要的。当然，此误差仅对跨越了闰秒时刻的外推有影响。

图3 两种TEME坐标系计算所得的相位角偏差比对Fig.3 Comparison between the solar phase angle deviations calculated under two TEME coordinate systems

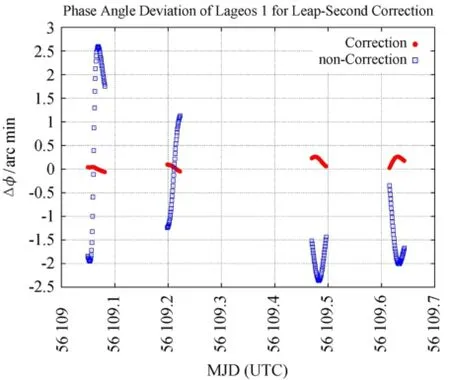
图4 闰秒修正后和未修正的相位角偏差比对Fig.4 Comparison between the solar phase angle deviations with and without the leap-second correction

3.3 相位角偏差示例

图5给出了STELLA卫星的相位角偏差的一个计算实例，分别给出了相位角偏差与测站高度角、外推时长的关系，相位角偏差以角分为单位，TLE根数对应的历元时刻为2012－12－21 07∶56∶11.777，双行根数中表征轨道所受阻力的参数B为－2.7910e-4。由图可见，在每一个过境圈次中，相位角偏差随高度角增加而增大；随着外推时间的延长，相位角的偏差总体增大，由1 d以内的6′增大到7 d以内的74′。

图5 STELLA卫星的相位角偏差示例Fig.5 A sample of the solar phase angle deviations of the STELLA

3.4 位置偏差平均值和相位角偏差的最大值

图6给出了LAGEOS 1卫星的位置偏差平均值和相位角偏差的最大值随双行根数的历元时刻的变化情况。由图可见，位置偏差较小，且随外推时间的延长并未明显变大。为了便于直观理解，将位置偏差的平均值对全年再次进行平均(下称“年均值”)，可得按1 d、3 d、7 d分别统计所得的位置偏差的平均值在全年的总体水平，计算得年均值分别为466 m、487 m、560 m，相应的相位角偏差的最大值亦较小，与位置偏差同样的方式计算年均值，分别为0.66′、0.85′、1.13′。

图6 LAGEOS 1卫星的位置偏差平均值及相位角偏差最大值Fig.6 Mean and maximum values of the solar phase angle deviations of the LAGEOS 1. (Left panel:Mean values.Right panel:maximum values)

图7给出了AJISAI卫星的位置偏差平均值和相位角偏差的最大值随双行根数的历元时刻的变化情况。与LAGEOS 1类似，位置偏差的平均值和相位角偏差的最大值均较小，位置偏差的平均值的年均值分别为570 m、608 m、722 m，与LAGEOS 1差别不太大，相位角偏差的最大值的年均值分别为2.28′、2.68′、4.42′，显著地大于LAGEOS 1，应归因于AJISAI的轨道高度明显低于LAGEOS 1。

图8给出了STELLA卫星的位置偏差平均值和相位角偏差的最大值随双行根数的历元时刻的变化情况。为了便于分辨，纵轴采用了对数坐标。可以明显看到位置偏差较大，尤其是第260 d以后(2012－09－17)，且随外推时间的延长偏差明显增大。由于第260 d后的偏差明显较大，将其分为第260 d前和第260 d后两段分别进行统计，第260 d前的位置偏差的平均值的年均值分别为789 m、1 004 m、1 986 m，第260 d后则分别为1347 m、3 293 m、11 731 m。相应地，相位角偏差的最大值亦较大，第260 d前的年均值分别为6.98′、13.22′、41.63′，第260 d后则分别为13.07′、50.47′、250.93′。可见对于STELLA这样的低轨卫星，在最差情况下已超出目前的精度要求，应引起重视。若采用1 d之内的双行根数进行计算则可以满足要求，但由于双行根数发布的滞后性，在事后处理时应重新下载较新双行根数数据，以缩短外推时长。

图7 AJISAI卫星的位置偏差平均值及相位角偏差最大值Fig.7 Mean and maximum values of the solar phase angle deviations of the AJISAI. (Left panel:Mean values.Right panel:maximum values)

图8 STELLA卫星的位置偏差平均值及相位角偏差最大值Fig.8 Mean and maximum values of the solar phase angle deviations of the STELLA. (Left panel:Mean values.Right panel:maximum values)

在双行根数中，是用一个参数B表征目标所受的阻力，对于中高轨卫星，主要来源于太阳光压的作用，对于低轨卫星，则主要来源于大气阻力。太阳光压相对比较稳定，大气阻力则变化较大，特别是大气密度的变化。显然B无法完全反应变化的大气的影响，因此低轨卫星的位置偏差较大，且随外推时间的延长而明显增大，尤其是该参数较大且变化较快时。图9给出了2012年LAGEOS 1、AJISAI、STELLA 3颗卫星的B值，LAGEOS 1和AJISAI卫星恒定为1.0e-4，STELLA卫星则变化较大，尤其是第260 d以后，这与上述比对计算结果适应。因此对于B较大且变化较快情况尤其需要注意，应尽可能采用1 d之内的双行根数计算。

4 分析及结论

综上所述，利用双行根数计算所得的相位角基本可以满足目前“度”量级的精度需求。对于LAGEOS 1、AJISAI这样的中高轨卫星，由于轨道较高、表征阻力的B恒定，计算所得的太阳相位角偏差较小，角分量级，且随外推时间的延长不会导致偏差明显增大；而对于STELLA这样的低轨卫星，因轨道较低、受变化的大气的影响显著，计算所得的太阳相位角偏差较大，尤其是当B比较大且变化较快时，偏差显著变大，且随外推时间的延长显著增大，在最差情况下，外推1 d的最大偏差约为13′，外推3 d约为50′，外推7 d约为251′，已超出目前的精度要求。

图9 B随TLE历元时刻的变化图Fig.9 Variations of Bwith days from the TLE epoch

因此，在事后分析中应尽可能使用1 d之内的双行根数计算太阳相位角，对于B较大且变化较快情况尤其需要注意，而从双行根数的发布频次来看是可行的，但双行根数的发布滞后，所以在事后处理时应重新下载较新双行根数数据进行计算以缩短外推时长。

另外，针对UTC闰秒的情况，本文提出了一种处理方法，即在双行根数外推时判断外推时段是否跨越了闰秒时刻，若跨越了则根据闰秒情况进行修正，相应的需要修改结果对应的UTC时间戳计算方法。

致谢：文中使用的SLR观测资料从国际激光测距服务(ILRS)获得，在此表示感谢。

[1] 唐轶峻，姜晓军，王建峰，等.三轴稳定GEO卫星漫反射光变特性[J].光子学报，2009，38(11):2863－2866.

Tang Yijun，Jiang Xiaojun，Wang Jianfeng，et al.Diffuse reflection optical characteristics of tress-axis stabilization GEO satellite[J].Acta Photonica Sinica，2009，38(11):2863－2866.

[2] 唐轶峻，姜晓军，卢晓猛，等.利用光照反射模型分析中高轨人造卫星测光特性[J].光学学报，2010，30(3):763－767.

Tang Yijun，Jiang Xiaojun，Lu Xiaomeng，et al.Analysis of photometric characteristics of medium and high apogee satellites based on light-reflection model[J].Acta Optica Sinica，2010，30(3):763－767.

[3] 韦栋，赵长印.SGP4/SDP4模型精度分析[J].天文学报，2009，50(3):332－339.

Wei Dong，Zhao Changyin.Analysis on the accuracy of the SGP4/SDP4 model[J].Acta Astronomica Sinica，2009，50(3):332－339.

[4] 刘卫，缪元兴.SGP4/SDP4模型预报可靠性分析[J].天文研究与技术——国家天文台台刊，2011，8(2):128－131.

Liu Wei，Miao Yuanxing.Tests of the accuracies of SGP4/SDP4 model predictions[J]. Astronomical Research＆Technology——Publications of National Astronomical Observatories of China，2011，8(2):128－131.

[5] Hoots F R，Roehrich R L.Spacetrack Report No.3:Models for propagation of NORAD element sets[R].Aerospace Defense Center，1980.

[6] Vallado D A，Crawford P，Hujsak R，et al.Revisiting Spacetrack Report＃3[R]//AIAA/AAS Astrodynamics Specialist Conference and Exhibit.Colorado，2006.

[7] McCarthy D D，Petit G.IERS Conversions(2003)[R].IERS，2004.

[8] 刘林，胡松杰，王歆.航天动力学引论[M].南京:南京大学出版社，2006:4－12.

[9] 李济生.人造卫星精密轨道确定[M].北京:解放军出版社，1995:1.

[10] Standish E M.Time scales in the JPL and CfA ephemerides[J].Astronomy＆Astrophysics，1998，336(1):381－384.

[11] Hilton J L，Hohenkerk C Y.Rotation matrix from the mean dynamical equator and equinox at J2000.0 to the ICRS[J].Astronomy＆Astrophysics，2004，413(2):765－770.

[12] 李荣旺，李语强.云南天文台的精密定轨系统[J].天文研究与技术——国家天文台台刊，2010，7(4):311－317.

Li Rongwang，Li Yuqiang.Precision orbit determination at the Yunnan observatory[J]. Astronomical Research＆Technology——Publications of National Astronomical Observatories of China，2010，7(4):311－317.

[13] Pearlman M R，Degnan J J，Bosworth J M.The international laser ranging service[J]. Advances in Space Research，2002，30(2):135－143.

An Analysis of Accuracies of TLE-Based Solar Phase Angles at Satellites

Li Rongwang，Li Yuqiang，Zhou Yu
(Yunnan Observatories，Chinese Academy of Sciences，Kunming 650011，China，Email:lirw＠ynao.ac.cn)

Photometry is one of the most important techniques to analyze physical characteristics of space objects.After-event analyses of photometric light curves of space objects and construction of their physical models all involve the solar phase angle，a parameter defined as the angle between the light incident onto an observed object from the sun and the light reflected from the object.Currently，the position of a space object is usually calculated with a Two-Line-Element(TLE)set.A position so calculated contains a systematic error increasing with the time elapsed from the TLE epoch.This raises the need to analyze the accuracy of the solar phase angle calculated based on the TLE.In this paper，we present comparison for the solar phase angles in the entire year of 2012 calculated using the TLE.The solar phase angles are those of the LAGEOS1，AJISAI，and STELLA，which are SLR(Satellite Laser Ranging)satellites of three representative apogee heights，respectively.For the three satellites we use the highly precise global SLR data as the standard descriptions of the orbits.Our results show that for the two satellites of relatively high orbits，the LAGEOS1 and AJISAI，their Bvalues(characterizing apparent resistance forces)were near constant，and their solar phase angle deviations remained on the level of arcminutes or below throughout the year；for the low-orbit STELLA its solar phase angle deviations were much larger，which can be attributed to influences of atmospheric changes.For the STELLA the deviations were particularly severe when Bvalues were large and changed rapidly.The deviations for the STELLA also increased dramatically with time from the TLE epoch.The worst-level deviations were about 13′after one day(from the epoch)，50′after 3 days，and 251′after 7 days，which are beyond currently acceptable precision limits.These results suggest that TLE sets within 1 day be used whenever possible in calculating solar phase angles，especially when Bvalues are large and in rapid change.We also present an approach to handle UTC leap seconds.The approach is to increase or decrease the time from the TLE epoch by 1 second if the time passes a leap-second moment，with the timestamp-calculation results consequently modified.

Solar phase angle；Photometry；Accuracy analysis；TLE；SLR

P135

A

1672－7673(2014)04－0369－09

2014－01－09；

2014－02－26

李荣旺，男，博士.研究方向:空间目标精密定轨.Email:lirw＠ynao.ac.cn