基于省际非平稳面板数据的中国碳库兹涅茨曲线实证研究

王 佳，杨 俊

（1．西南财经大学 财政税务学院，四川 成都 611130；2．重庆大学 经济与工商管理学院，重庆 400030）

基于省际非平稳面板数据的中国碳库兹涅茨曲线实证研究

王 佳1，杨 俊2

（1．西南财经大学 财政税务学院，四川 成都 611130；2．重庆大学 经济与工商管理学院，重庆 400030）

将化石能源细分为17种，并考虑水泥生产，计算了1997—2011年中国各省的二氧化碳排放指标，利用面板单位根检验、面板协整检验、FMOLS方法检验了著名的碳库兹涅茨曲线（CKC）在中国的适用性，结果表明：CKC各变量在统计上显著存在协整关系；大部分地区存在CKC，但基本都未达到拐点，处于上升阶段；CKC的理论拐点为540 365元，中国在2020年左右才能步入碳排放下降区间。

碳库兹涅茨曲线；面板协整；FMOLS

一、引 言

改革开放30余年的经济持续快速增长，造就了“中国奇迹”，并在2010年成为世界第二大经济体，但是能源和环境的双重约束日趋强化。从能源消费来看，中国已由1978年的57 144万吨标准煤，骤升至2011年的348 002万吨标准煤（《中国统计年鉴2012》），增加了6倍多，2008年中国已经成为世界上煤炭消费第一大国和能源消费第一大国。中国碳排放量占世界碳排放总量的比重也不断增加。根据美国能源部CO2信息分析中心（CDIAC）的数据，2005年中国成为全球CO2排放第一大国，2008年CO2排放量更是占到全球的23．55%；据世界资源研究所（WRI）的测算结果，2007年中国二氧化碳排放量已居世界第一位。在此背景下，中国政府2009年主动承诺，到2020年，单位 GDP碳排放量比2005年下降40%～45%，并将其作为约束性指标写进“十二五”规划。要实现低碳发展，必然需要重点关注经济增长与CO2排放的长期变化趋势。

学界通过环境库兹涅茨曲线（EKC）的研究来探讨经济增长与环境污染之间的关系，进而延伸到对碳库茨涅茨曲线（Carbon Kuznets Curve，CKC）的研究。Grossman and Krueger、Panayotou、Selden and Song等从实证角度认为环境污染和经济增长呈现出典型的倒“U”关系，即在经济发展的初级阶段，随着经济增长，环境质量不断恶化，当经济增长越过某一特定的“转折点”时，环境质量将得到改善［1－3］。近年来，温室气体排放引发一系列气候变化，各国政府及学术界更加关注碳排放问题，Selden and Song等多位国外学者提出了碳排放库兹涅茨曲线，并验证它的存在性以及探究其形状 ，但也有不少学者如Agras and Chapman等提出质疑，认为并不存在CKC［4］；而Galeotti等对CKC进行了稳健性检验，发现 OECD国家存在CKC［5］，Moomaw and Unruh等却发现两者呈 N型［6］。

国内学者也对CKC进行了有意义的探究。付加锋等基于生产和消费视角，认为无论是从生产视角还是从消费视角，单位GDP的CO2排放量都具有显著的“倒U”形状［7］。蔡昉等通过拟合CKC、估计排放水平从升到降的拐点考察了中国经济内在的节能减排要求，认为如果温室气体的减排被动等待库兹涅茨拐点的到来，将无法应对日益增加的环境压力［8］。林伯强使用世界银行的时间序列数据研究中国CO2排放拐点，并对其在不同条件下的实现情况进行了预测［9］。许广月利用因素分解法估算省级面板碳排放数据，对中国东中西三大区域的碳排放库兹涅茨曲线进行验证，发现存在区域差异［10］。虞义华等分析了CO2排放强度同经济发展水平及产业结构之间的关系，认为碳排放强度与人均GDP之间存在“N”形关系［11］。

在已有研究的基础上，本文将从以下几个方面进行探索：以往通过能源消费计算CO2排放量，最多细分为9类，本文囊括了《中国能源统计年鉴》中涉及的17种能源种类，还考虑了水泥生产过程带来的CO2排放；基于中国1997—2011年的省际非平稳面板数据，重点关注CKC问题中的时间特征，通过较为前沿的面板单位检验、面板协整检验及估计等计量分析技术，来验证中国碳排放库兹涅茨曲线存在与否，希望得到更有说服力的证据，为中国碳减排战略的制定和实施提供决策参考。

二、模型设定与数据说明

（一）CKC的计量模型设定

学术界常用的EKC模型主要为对数多项式形式，解释变量一般包括收入水平的一次项到三次项和其他控制变量。绝大多数学者倾向于采用Selden and Song）提出的设定方法研究EKC问题，其表达式如下［3］：

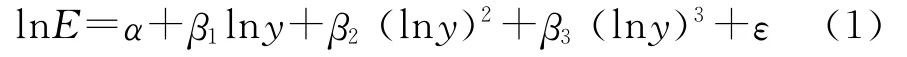
E为环境污染物，本文将其设定为CO2，则EKC转化为CKC；y为收入水平，通常用人均GDP来表示；其他符号的意义与通常的计量经济学模型设定相同。但是Poon等发现，工业化国家的CKC会呈现出较明显的三次形式，而发展中国家往往表现为“倒 U”型的二次多项式，即［12］：

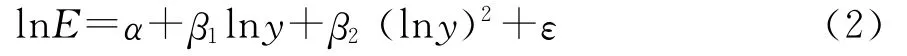
同时，CKC三次对数多项式模型可得到两个转折点，但其并没有准确的经济学意义，故本文选择“倒U”型的二次多项式：

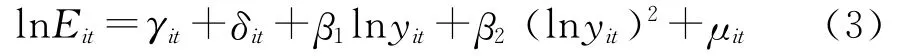
其中，下标i代表省份，t代表年份，方程右边前面两项分别代表对应的个体效应和时间效应；E表示CO2排放度量指标，通过人均CO2排放量（CP）来表示；y为经济发展水平，通常用人均GDP来度量。

需要说明的是，Banerjee等发现若面板数据各变量在时间维度上为同阶单整过程，则传统CKC模型的参数估计值的有效性不足，这时需采用动态面板数据模型，以得到稳定的长期均衡关系［13］67－68。使用该模型的前提条件是所有变量均为一阶单整过程，且具有协整关系和较大的个体数和时序数。本文第三部分将进行多种面板单位检验和面板协整检验，并详细加以分析和阐述。

（二）CO2排放测算方法

中国官方或权威机构并未公布CO2排放量的计算标准和中国地方CO2排放数据。最著名、应用最广泛的方法，是联合国政府间气候变化专门委员会（IPCC）2006年编制的《国家温室气体清单指南》中提供的三种方法。根据美国能源部CO2信息分析中心（CDIAC）①详见http：／／cdiac．ornl．gov／trends／emis／meth＿reg．html。2012年公布的数据，2010年中国水泥生产带来的CO2排放超过了10%，已不容忽视，因此本文主要关注由于化石能源燃耗和水泥生产两个环节带来的CO2排放。

在测算方法上，本文选取《2006年IPCC国家温室气体清单指南》提供的三种方法中的方法1。化石能源燃烧引起的CO2排放量计算公式如下：

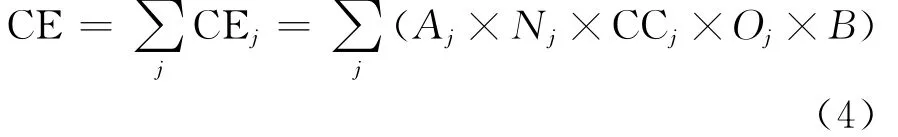
其中CE为各类化石能源消费的CO2排放总量；j为化石能源的种类；Aj为第j种化石能源的消耗量；Nj为第j种化石能源的发热值；CCj为第j种化石能源的含碳量；Oj为第j种化石能源的氧化因子；B为CO2分子与C元素质量比，即44／12。

其中CC为水泥生产过程中的CO2排放总量；Q为水泥生产量；r为水泥产品中熟料的比重；a为水泥生产CO2排放系数。

（三）数据说明

中国地区能源消耗量来自历年《中国能源统计年鉴》中的“地区能源平衡表（实物量）”。考虑数据的可得性和可比性，获取了1997—2011年各省的数据；由于缺少西藏、台湾、香港、澳门的统计资料，共得到30个省份的对应数据。另外，为避免以往简单的一次能源划分方法导致误差偏大，本文将《中国能源统计年鉴》中的所有能源都包含在内，有原煤、洗精煤、其他洗煤、型煤、焦炭、焦炉煤气、其他煤气、其他焦化产品、原油、汽油、煤油、柴油、燃料油、液化石油气、炼厂干气、其他石油制品和天然气，共17种。由于中国能源统计采用的低位发热量，故本文Nj为低位发热量，其数据来源于《中国能源统计年鉴2011》附表4，CCj和Oj的数据为缺省值。

水泥行业的碳排放除来自于能源消耗外，原料的分解（主要指碳酸盐）也会释放出较多的CO2，也就是水泥中的硅酸盐熟料才会产生排放。文中各地区的水泥产量来源于历年《中国统计年鉴》以及各省份统计年鉴；根据中国水泥行业协会的年度统计资料，r（熟料比重）在2006年之前取值0．70，之后取值为0．60；除了特别说明外，本文其他基础数据均来源于历年各省份统计年鉴。

需要说明是，本文的人均指标均以常住人口计算，以货币为单位的指标都以2011年为基期进行了价格调整。

三、实证分析

如前所述，本文最终收集整理了中国1997—2011年30个省级截面（未包括西藏、香港、澳门和台湾）组成的强平衡面板数据集，样本总数达到了420次。

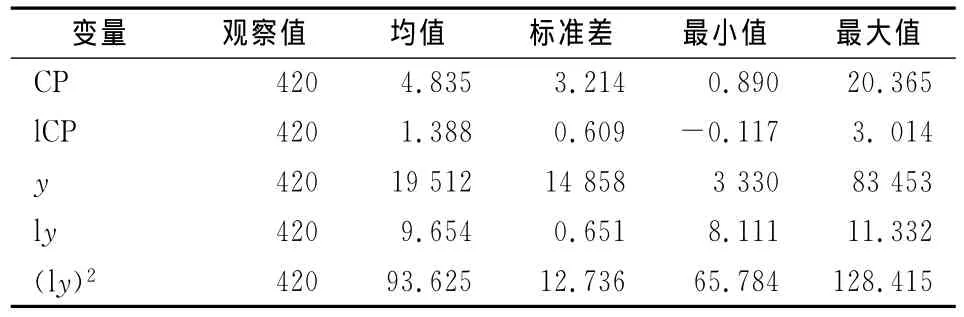
表1 CKC主要变量的描述性统计表

如表1所示，人均CO2排放量CP和人均地区生产总值y的水平值变异程度很大，出现结构变化的可能性较大。相比而言，它们的自然对数值变异程度相对小一些，但绝对值适合回归分析。从图1看，lCP和l y 并不呈现线性关系，而lCP 和（l y）2的关系也不明确，但肯定是密切相关的。显然，CKC的设定是有理由的，只是形式需要进一步分析来确定。

（一）个体效应检验

面板数据面临是否可以将数据混合的问题，不同地区或时期可能具有不同的性质，故本文所使用的面板数据在回归前需对其进行检验。为了确定使用混合回归还是面板数据模型，首先需要对数据进行固定效应模型的设定，并求出聚类稳健标准差，再通过虚拟变量（LSDV）法观察截面虚拟变量的各自及联合的显著程度。

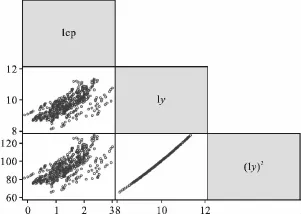
图1 主要变量散点矩阵图

本文通过计量经济学软件Stata 12来实现这一过程，结果显示：大部分省份（23个省份）虚拟变量在5%水平上显著，故要拒绝“所有个体虚拟变量都为0”的假定，即认为存在个体效应，不能将数据混合回归分析。为了得到更为稳健的检验结果，本文另外选取了最为流行的三种方法：截面相关性联合显著性的F检验、Breusch—Pagan的拉格朗日乘子（LM）检验以及似然比（LR）检验，诸检验的零假设情况及结果见表2。

表2 个体效应检验结果表

根据表2的估计结果，三种检验的显著水平均为0%，即都强烈拒绝“不存在个体效应”的假设，表明该面板数据不能混合估计，应该考虑面板数据模型。

（二）面板单位根检验

由于该面板数据时序较长，有可能是非平稳的，但时间序列数据的单位根检验未考虑截面因素，而且基本上都是渐进分析，即基于大样本。近年来兴起的面板单位根检验主要改善了小样本带来的问题，考虑了截面因素，提高了检验功效。面板单位根检验按照出现时间可以分为两个阶段：第一代检验提出较早，要求横截面独立，又分为相同根假设和不同根假设，前者主要为LLC检验、Breitung检验、Hadri检验，后者主要有IPS检验、Fisher－ADF检验、Fisher－PP检验；第二代检验假设存在横截面相关的空间效应，考虑横截面异质性和横截面相关性，如Pesaran提出的CADF检验。为了避免单一检验的局限，本文兼顾了相同根、不同根的各类情况，使用了七种检验来检验各变量是否平稳。检验结果见表3。

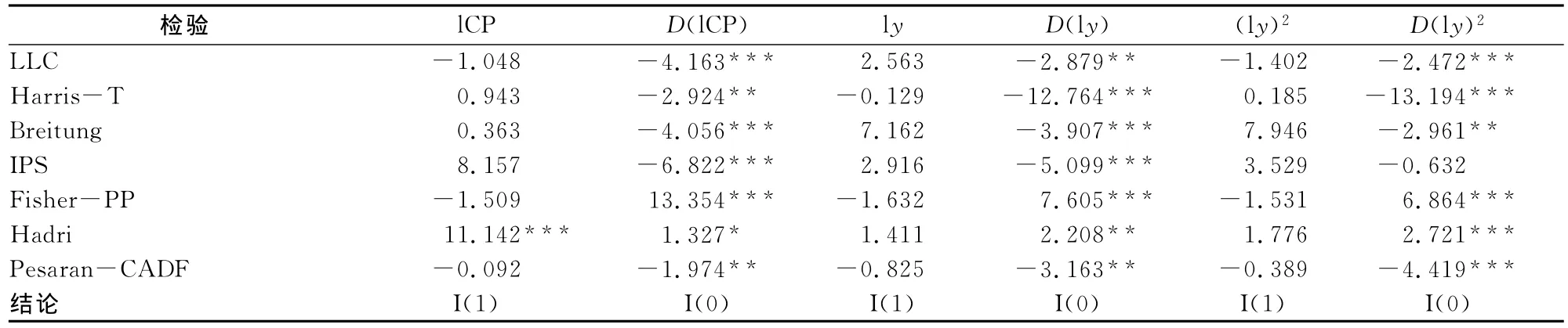
表3 面板单位根检验结果表

LLC检验、Harris－T检验、Breitung检验、IPS检验、Fisher－PP检验、Hadri检验及Pesaran－CADF检验的零假设均为存在单位根，不同的是：LLC检验、Harris－T检验、Breitung检验和Pesaran－CADF检验的零假设为同质面板单位根，即截面系数相同的单位根；IPS检验、Fisher－PP检验和Hadri检验的零假设是异质面板单位根，即截面系数不相同。

从检验结果看，l y在七种检验中都接受了原假设，即存在单位根过程，而其一阶差分值D（l y）均在5%的显著水平以上拒绝原假设，甚至Harris－T检验、Breitung检验、IPS检验和Fisher－PP检验在1%水平上显著拒绝了原假设，可以确定该变量为一阶单整，即为I（1）过程。lCP和（ly）2则有一种检验未通过。对于lCP，除Hadri检验之外的其他六个检验都显示了同一结果，水平值接受存在单位根过程的假设，一阶差分值至少在5%水平上拒绝原假设。（l y）2则是IPS检验未通过，其他检验的结果表现良好。对这两个变量而言，七种面板单位根检验只有一种检验未通过，显然是可以接受的，毕竟本文使用的面板数据的时序只有14年，这可能影响了某些检验的功效。

综合看来，3个变量均存在单位根，其一阶差分值是平稳的，也就是说均为同阶单整，其线性组合可能存在协整关系，有必要进行面板协整检验。

（三）面板协整检验

一般说来，国内外研究主要使用两类面板协整检验方法：一类基于EG两步法，对同质面板和异质面板都适用，比如国内学者经常使用Pedroni检验和Kao检验。前者利用协整方程，估计截面之间不同的斜系数、固定效应系数和个体确定趋势系数，利用7个Panel Data的协整统计量对回归残差进行平稳性检验；后者是基于回归残差的LM检验，不同的是其零假设是面板存在协整关系。另一类基于Johansen统计量，形成异质面板的似然比（LM），如Fisher型联合p值协整检验，但是上述检验不适用于具有截面相关的面板数据。因此，Westerlun运用自举抽样技术（bootstrap）改进LM 方法的检验功效，并于2008年构建了基于误差修正模型的协整检验［14］。为了克服使用单一检验方法的弊端，本文主要采用Pedroni检验、Kao检验、Fisher检验及Westerlund检验，综合判断各变量是否存在协整关系。

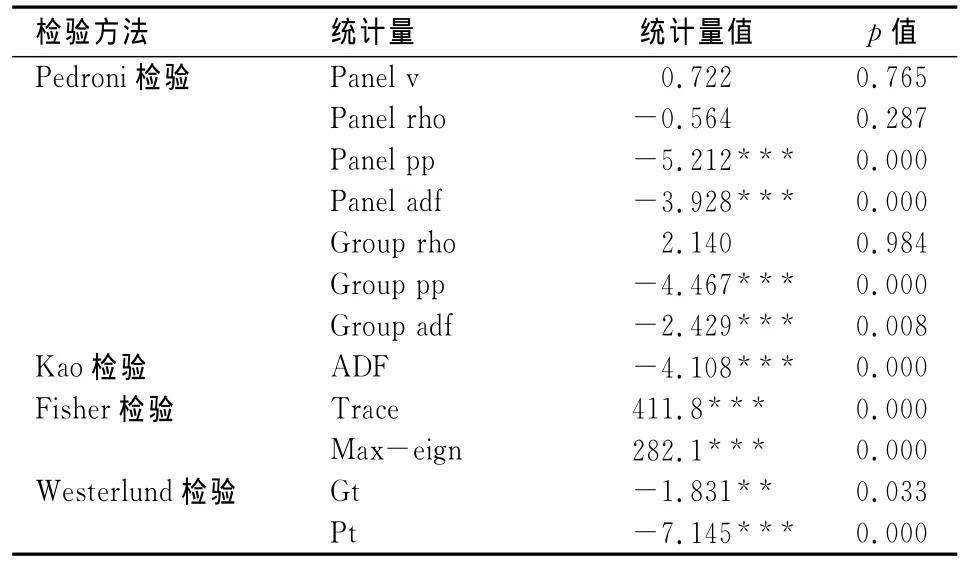
表4 面板协整检验结果表

如表4所示，Pedroni检验结论并不一致，四种联合组内统计量、三种组间统计量分别有2个、1个无法拒绝无协整关系的原假设。Pedroni证明，在小样本中，Panel adf、Group adf统计量检验效果最好，Panel v、Group rho统计量检验效果最差，其他处于中间。在七个统计量中，Panel adf、Group adf、Group pp以及Panel pp统计量都在1%的显著性水平下拒绝原假设；Panel v、panel rho和 Group rho统 计 量 即 使 在10%的水平上也不能拒绝原假设。考虑到本文数据样本偏小，Panel v、Group rho这两个统计量可以不予以考虑，而剩余5个统计量中，有4个统计量至少在1%显著水平上拒绝原假设，包括Panel adf、Group adf这两个在小样本中效果最好的统计量。因此，Pedroni检验显示变量之间存在协整关系，而同质面板Kao检验、异质面板Fisher检验以及包含截面相关的Westerlund检验都认同协整关系的存在。综合考虑多种检验结果可以得出：模型（3）中各变量存在协整关系，即存在长期共同趋势。

（四）面板协整估计结果及分析

前述面板单位根检验、异质性检验和面板协整检验的结果表明，数据是不平稳的且变量之间存在长期协同关系。面板协整估计方法有助于改善变量内生性及序列相关所导致的伪回归问题。考虑到我们的样本容量偏小和非平稳性，本文选用Pedroni发展完善的修正最小二乘法（Fully Modified OLS）来估计变量的长期关系。简单介绍一下思路：首先分别对各个截面用FMOLS进行估计，然后再进行面板协整系数的估计，并对其OLS估计的系数进行非参数估计。Pedroni提出的截面间均值估计方法考虑了面板组间维度，提供了协整方程共同参数值的一致检验，优于混合面板估计方法。在蒙特卡洛数值模拟过程中，估计的协整参数渐进无偏、一致，且具有稳健的有限样本性质，对数据的异质性也有很好的包容性。

按照Pedroni的说法，FMOLS主要估计联合组间（between－dimension）系数，实际上就本文而言，联合组间估计就是对地区之间诸变量系数的均值进行估计。从表5的估计结果看，CKC中主要变量l y和（l y）2系数的组均值在1%置信水平上统计显著，而且l y 的符号为正、（l y）2符号为负，说明估计结果基本符合预期。具体说来，30个省份中有23个省份参数估计的符号与预期一致，其中19个省份的系数组内均值均在5%置信水平上统计显著，而且l y 的符号为正、l y）2符号为负。l y 和（l y）2均非常显著，F统计量同样非常显著，显示回归分析的拟合结果较好，符号分为正和负。可以说，估计结果在统计上验证了CKC的倒U曲线的假设。

众所周知，中国地区之间经济发展呈现极强的不均衡态势，这一特征也体现在CKC方程中。除了地区经济发展存在异质性外，产业结构、能源消费结构、清洁技术水平、国际贸易结构等方面也存在较大差异，导致地区CKC的具体形式也不尽相同。在本文所涉及的30个省份中，统计上显著的21省份主要是两类地区，即经济发达地区和欠发达地区。表5未列出的11个省份体现出这样的特征：经济发达省份和碳密集产业比重高的地区，有山东、河北等；化石资源尤其是煤炭资源比较丰富的地区，有山西、河南、新疆、四川、甘肃等。表5中19个省份的参数估计值差距也较大。以l y为例，最小值为1．265，最大值为14．710，后者是前者的将近12倍。可见，即使存在CO2排放库兹涅茨曲线，各地区的差距也相当大，这与地区非均衡发展的特征相呼应。

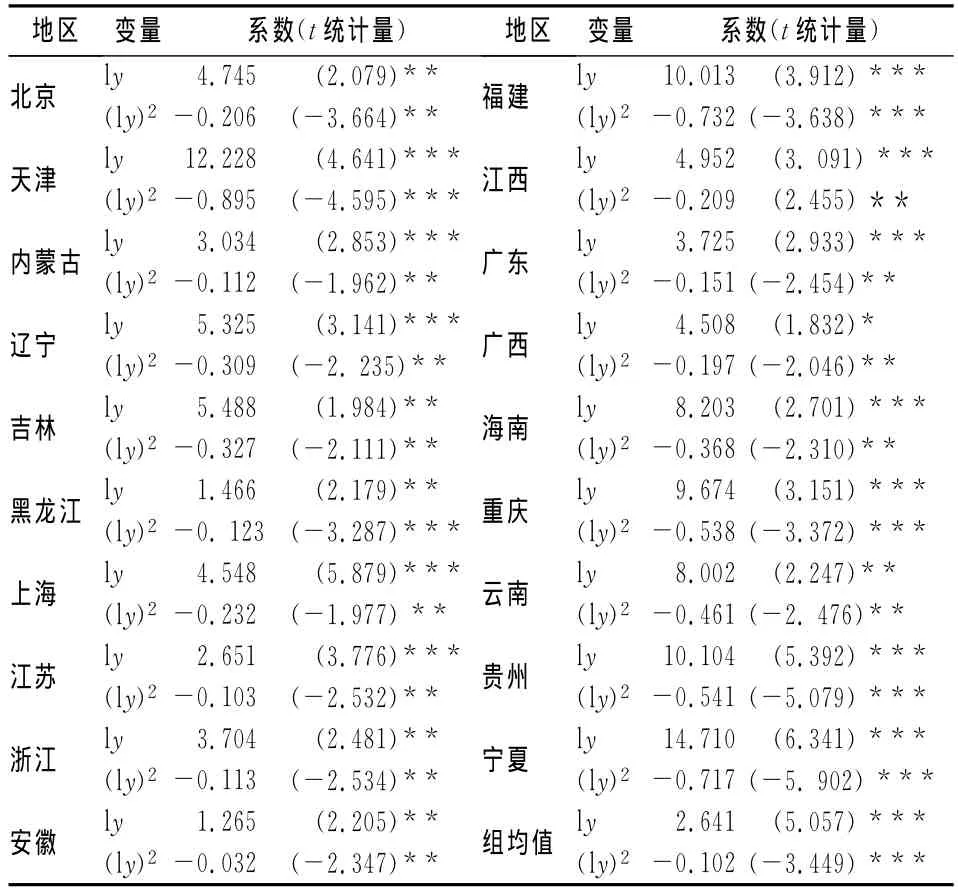
表5 FMOLS面板协整估计结果表① 这里只给出了统计上显著的省份的回归结果，不显著的省份的回归结果可以向作者索要。

下面来确定CO2排放库兹涅茨曲线的拐点。由式（3）可以计算出CO2排放开始下降的拐点为exp（－β1／2β2）。根据表5，得到中国碳排放下降的拐点为人均 GDP 540 365元（2011年价），与此对应的是2011年中国人均GDP均值为29 992元，这与拐点相差甚远，也就说中国尚未达到碳排放的峰值。尽管从地区层面看，某些省份已经达到了这个人均GDP水平，但是这个拐点主要是针对均值的，并不能说明全国已达到了拐点。譬如，北京人均地区生产总值从2005年开始超过了540 365元，但是根据表5中的组内回归结果，北京市的拐点应该为100 407元。根据十八大报告，2020年GDP总量预期在2010年基础上翻一番，假设人口基本保持不变，那么人均GDP也翻一番，达到59 984元，超过了本文中的CKC拐点，这意味着在2020年左右，准确地说是在2019年，中国将达到CO2排放高峰，并从此开始下降。当然，这一结果与林伯强和蒋竺均的结果相吻合［9］。

四、研究结论

本文将化石能源种类细分为17类，并考虑了水泥生产过程带来的CO2排放，较为精细的计算了中国1997—2011年30个省份的碳排放数据，并基于这一面板数据，利用面板单位根检验、面板协整检验、FMOLS方法对碳排放与经济发展水平之间的长期关系进行了实证研究，检验了著名的碳库兹涅茨曲线在中国的适用性，得到如下结论：

第一，非平稳的面板数据lCP、l y 和（l y）2之间显著存在协整关系，FMOLS协整估计结果显示存在长期均衡关系。中国碳排放库兹涅茨曲线在现实中是存在的，呈现倒U型特征，且长期稳定。大部分地区存在CKC，但基本都未达到拐点，处于上升阶段，CKC在中国的适用性有待进一步观察。

第二，碳排放与经济发展水平的长期关系推导出CKC的拐点为人均GDP540 365元，尽管少数发达省份接近此拐点，但全国整体水平将在2020年左右才能步入碳排放下降区间。地区之间到达CKC拐点的时点并不相同，地区协整估计结果显示拐点差距较大。

总之，中国尚处于碳排放上升期，随着经济发展水平的提升，碳排放总量仍会增加。尽管理论上表明拐点在2020年左右出现，但是该拐点并不会自然发生。从能源消费的实际情况进行预测，如果保持现状的经济社会发展模式不变，碳排放高峰在2020年不会出现。政府应该有所作为，坐等CKC达到拐点是不可能的，必须在提高能源使用效率、优化能源消费结构、加快产业结构升级等方面花大力气，以期CKC拐点提前到来。另外，需要重视地区碳排放差异，深化碳交易机制的改革，加大环境规制力度，避免碳排放的区域转移，缩小地区间碳生产率的差距，争取早日达到碳减排目标。

［1］ Grossman G M，Krueger A B．Economic Growth and the Environment［J］．Quarterly Journal of Economics，1995，110（2）．

［2］ Panayotou T．Empirical Tests and Policy Analysis of Environmental Degradation at Different Stages of Economic Development［R］．Geneva：ILO，Technology and Employment Program，1993．

［3］ Selden T M，Song D．Environmental Quality and Development：Is There a Kuznets Curve for Air Pollution［J］．Journal of Environmental Economics and Management，1994，27（2）．

［4］ Agras J，Chapman D．A Dynamic Approach to the Environmental Kuznets Curve Hypothesis［J］．Ecological Economics，1999，28（2）．

［5］ Galeotti M，Lanza A，Pauli F．Reassessing the Environmental Kuznets Curve for CO2Emissions：A Robustness Exercise［J］．Ecological Economics，2006，57（1）．

［6］ Moomaw W R，Unruh G C．Are Environmental Kuznets Curve Misleading US？The Case of CO2Emissions，Special Issue on Environmental Kuznets Curves［J］．Environmental and Development Economics，1997，2（4）．

［7］ 付加锋，高庆先，师华定．基于生产与消费视角的CO2环境库茨涅兹曲线的实证研究［J］．气候变化研究进展，2008（6）．

［8］ 蔡昉，都阳，王美艳．经济发展方式转变与节能减排内在动力［J］．经济研究，2008（6）．

［9］ 林伯强，蒋竺均．中国二氧化碳的环境库兹涅茨曲线预测及影响因素［J］．管理世界，2009（4）．

［10］许广月，宋德勇．中国碳排放环境库兹涅茨曲线的实证研究——基于省域面板数据［J］．中国工业经济，2010（5）．

［11］虞义华，郑新业，张莉．经济发展水平、产业结构与碳排放强度——中国省级面板数据分析［J］．经济理论与经济管理，2011（3）．

［12］Poon J P H，Casas I，He C F．The Impact of Energy，Transport，and Trade on Air Pollution China［J］．Eurasian Geography and Economics，2006，47（5）．

［13］Banerjee A et al．Co－Integration，Error－Correction，and the Econometric Analysis of Non－Stationary Data［M］．Oxford：Oxford University Press，UK，1993．

［14］Westerlund J．Testing for Error Correction in Panel Data［J］．Oxford Bulletin of Economics and Statistics，2007，69（6）．

An Empirical Study on Carbon Kuznets Curve in China Based on Nonstationary Heterogeneous Provincial Panel Data

WANG Jia1，YANG Jun2
（1．School of Public Finance and Taxation，Southwestern University of Finance and Economics，Chengdu 611130，China；2．School of Economics and Business Administration，Chongqing University，Chongqing 400030，China）

On the basis of subdividing 17fossil energy types and considering emission sources of cement production，we have estimated sub－national carbon dioxide emission index from 1997to 2011．Further，we have tested whether famous carbon Kuznets curve（CKC）existed in China，application on panel unit root test，panel cointegration test and fully modified OLS．The results are as follow：there are significant cointegration relation statistically between variables；CKC do exist in most regions in China，but don＇t basically approach to break point，i．e．the trendy of ascent stage；the average break point is 540 365yuan，meanwhile，carbon Dioxide emission will step into descent range in China．

carbon kuznets curve；panel cointegration；fully modified ordinary least squares

F224．0

A

1007－3116（2014）04－0037－07

2013－11－18

国家自然科学基金重点项目《天然气资源的经济安全重大问题与对策研究》（71133007）；国家自然科学基金面上项目《基于市场交易的天然气开采量与成本协调激励气价机制研究》（71373297）

王 佳，男，河南修武人，经济学博士，讲师，研究方向：资源环境经济学，数量经济学；

杨 俊，男，重庆铜梁人，教授，博士生导师，研究方向：能源环境经济学，电力技术经济学。

（责任编辑：杜一哲）