中国现阶段环境约束下的适度经济增长率研究——基于废气排放量视角的分析

李宝瑜，刘 洋

（山西财经大学 统计学院，山西 太原 030006）

中国现阶段环境约束下的适度经济增长率研究
——基于废气排放量视角的分析

李宝瑜，刘 洋

（山西财经大学 统计学院，山西 太原 030006）

经济发展与环境污染的关系历来都是一对不可回避的矛盾，也是学术界研究的热点，国内外大多数学者都在考察人均GDP与环境污染的库兹涅茨曲线，但对于环境与经济增长率的关系却很少有人研究。首先建立环境变量与经济增长率关系的变参数状态空间模型，并将建立的状态空间模型转化成线性规划中的决策方程，之后应用参数区间估计和集合论两种方法，通过约束相应的变量及变量的系数来估计中国现阶段环境约束下的适度经济增长率。

适度经济增长；环境约束；状态空间模型；线性规划模型

一、引 言

改革开放以来，中国的经济增速举世瞩目，同时，高增速所带来的环境污染也越来越严重。因此，我们必须思考环境和经济之间到底是怎样的关系，经济加速发展是否必然带来环境污染，先污染后治理的规律能否打破。

关于经济发展和环境污染的关系，主要围绕环境库兹涅茨曲线展开。该理论认为，环境污染与经济发展呈倒“U”型曲线（环境随着经济的发展会经历一个先恶化后改善的过程），通常采用的变量是人均国民收入或相应经济总量。然而，还有另一条研究路径常常被人忽视，这就是经济增长率与环境污染的关系研究。从不同国家的数据可以看出：增长率与不同的环境变量呈现的是一种具有不同斜率的线性关系，绝不是随着经济增长率的提高，环境污染呈现先走高、后平稳、然后再下降的倒“U”型曲线关系。既然环境污染与增长率之间呈线性关系，就必然出现要加速经济发展就必须付出环境代价的问题，经济与环境就会陷入一种矛盾之中。那么，是否存在一个能够使二者互相妥协，共生共进的适度经济增长率呢？能否找到一个污染最小条件下的适度经济增长率区间？本文将通过建立模型，寻找环境约束下的适度经济增长率。

二、文献综述

在环境与经济关系这个大命题下，有着众多不同的研究路径。1991年美国经济学家Grossman和Krueger提出经济发展与环境发展的关系呈倒“U”型曲线关系的理论，围绕这一现象是否具有普遍意义，经济增长是否可以避免环境污染的问题就出现了很大的争论。一些学者认为环境库兹涅茨曲线（EKC）不可避免，而另一些学者则认为可以打破。支持环境库兹涅茨曲线存在的学者Markus等，从经济规模、结构、技术、收入差异、国际贸易与环境关系的理论角度证明环境倒“U”型曲线的存在［1］。另一些不支持环境库兹涅茨曲线的学者如Dasgupta等，通过实证研究发现某些污染物与人均收入水平没有倒“U”型关系，而是线性甚至“N”型关系［2］。

在中国，这些年来经济增速创造了世界奇迹，但是否进入了倒“U”型轨道？先污染后治理的规律是否能够被打破？不同的人对此也有不同的看法。中国一些学者注意到EKC曲线是经验数据的描述，并不能说明人均收入和环境之间存在必然联系。不同的省份和环境变量会呈现不同的曲线。他们通过理论与实证研究认为EKC曲线并不存在［3］。

环境与经济增长的另一路径是将环境变量引入内生经济增长模型所做的研究。自从20世纪80年代中后期以来，以Romer、Lucas等人为代表的内生增长模型的出现，经济学家们开始将环境变量引入生产函数，把环境质量引入效用函数，进而在内生增长模型框架下讨论环境恶化与经济可持续发展问题。代表模型有：Bovenberg等在Romer模型的基础上将环境变量引入生产函数的模型，Ligthart通过将“AK”模型进行扩展来研究环境污染外部性与经济持续增长问题，Grimaud等将环境污染和有限的不可再生资源引入新熊彼特模型的研究。上述叙述均参考Panayotou的综述［4］。

而国内对于该问题的研究较少，大多是在国外研究成果的基础上进行模型改进。梅国平等将环境质量内生化，构建Hamilton动态优化模型寻求均衡状态［5］；岳书敬等使用三种不同的模型，考察了在环境因素的约束下，工业的增长效率及其影响因素［6］；也有使用面板数据进行省际间的实证研究。

关于环境约束下的经济增长问题，国内外的研究主要有两种研究思路：是研究环境库兹涅茨曲线是否可以避免；二是在内生经济增长模型的基础上，使用动态优化方法进行求解，得出在相应条件下经济能够持续增长的结论。相应的研究都是在求解过程中使用经济总量为研究对象，得出了固定的经济增长率，并没有直接对经济增长率进行研究。本文拟直接对经济增长率与环境变量的关系进行研究。

为了求证二者关系，首先需要找到一个环境典型变量和一个经济增长变量。经济增长变量可以用目前通行的GDP增长率来度量，环境变量则比较复杂。环境污染有多个方面，每个方面都是以物质计量单位统计的，这些方面目前还难以货币化计量，也缺乏一个综合指标，所以我们选择用某个典型变量作为环境代表变量，本文选用废气排放量进行实际建模和分析。而对于环境的其他变量，诸如废水排放量或者其它某个环境指标与经济增长率的关系，也可参照本文的方法进行建模和分析，原理类似。

本文设计了一套废气排放约束下的经济增长模型，完整的方案包括两个模型和两种方法。具体思路为：建立状态空间计量模型估计环境（废气排放）与经济增长的关系；将估计得到的环境模型作为目标函数建立线性规划模型，给出约束条件；在各种细分约束条件下，求解多维约束和单项约束下的适度经济增长率；使用区间估计和集合求交集法，分别求解多维约束下和多个单项约束下的适度经济增长率区间。

三、用状态空间模型估计环境与经济增长率的关系

（一）变量与模型选择

经验证明，如果以年度作为研究对象，经济增长率对环境有显著的影响，然而环境对经济增长率的影响尽管存在，但它却是一个缓慢和复杂的过程，不一定表现在年度对应关系上，不过环境变化自身却可能在时间上有连续性，即本期的环境受前期影响较大。基于这种考虑，我们选择能够反应环境连续变化的以环境变化作为被解释变量的可变参数状态空间模型。

环境变化特别是空气质量变化不仅受经济增长率的影响，同时还受其它因素的影响，如城镇化速度、能源消耗水平、经济增长对环境的弹性系数等，以环境变量作为被解释变量时，还必须选择相关解释变量。

我们以工业废气排放总量对数（lnFQ）作为环境变量，经济增长率（ZZL）、城镇化率（CZHL）、能源强度（NYQD）、lnFQ的滞后一期作为解释变量，分别从增长速度、城镇化水平和生产技术水平三个方面来解释经济发展造成的污染和影响，建立如下状态空间模型：

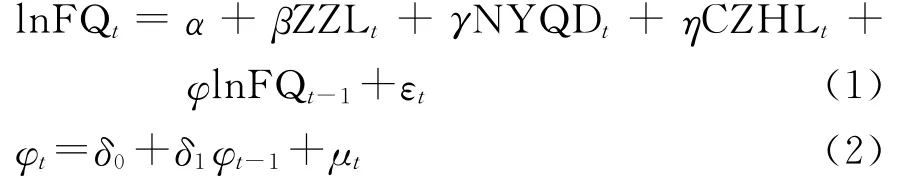
其中式（1）是量测方程，反映了各要素与废气排放总量的关系，α是截距项，β、γ、η分别表示废气排放总量对经济增长率、能源强度和城镇化率变动的敏感程度，εt是均值为0、协方差连续不相关的扰动项；φ为可变参数，反映各个时点上废气排放总量受前一期影响的程度。式（2）为状态方程，描述了可变参数φ的生成过程。

（二）数据的预处理

本文选择的数据为年度数据，相应的原始数据均可从历年《中国统计年鉴》获得，在建立模型之前需要对所选择的指标数据进行一定的预处理。

工业废气排放总量对数（lnFQ）：中国从1985年开始公布环境污染的相关数据，我们可以从《中国统计年鉴》和《环境统计年鉴》获得工业废气排放总量（亿标立方米）1985－2010年的数据，但是从2011年开始中国不再公布工业废气排放总量，改为公布废气中主要污染物的排放情况，包括二氧化硫、氮氧化物和烟（粉）尘，单位为万吨。数据公布口径的变化使得工业废气排放总量这一指标2011年的数据缺失，本文以2011年中国工业的增长率代替工业废气排放总量的增长率，计算出2011年的工业废气排放总量来弥补数据的缺失。对废气排放总量序列取对数，得到lnFQ序列。

经济增长率（ZZL）：本文选用的增长率指标为全国GDP剔除价格因素的环比经济增长率。

城镇化率（CZHL）：按照惯例，城镇化率这一指标用城镇人口占总人口的比重来表示。中国城镇化率的变化比较稳定，但在1995年存在一个拐点，1995年之前基本以每年0．5%的速度增长，在此之后，每年上升约1．4%。这种数据上的异常可能跟统计口径的变化有关，并不符合实际情况。因此，本文以1995年的数据为基础，用1995年至2011年中国城镇化率的平均变化速度代替之前的变化速度，得到了消除拐点的城镇化率序列。

能源强度（NYQD）：能源强度即单位GDP能耗，单位是吨标准煤／万元。中国只公布了各省份的万元GDP耗能，并没有全国的能源强度水平，因此需要用全国的GDP和能源消耗总量来计算。为了保证各年能源强度的可比性，首先对GDP进行价格平减，将各年的GDP换算为2011年的价格水平，再用能源消耗总量除以GDP计算能源强度的值。

（三）模型的估计

1．变量的平稳性及协整关系检验

状态空间方法构造的变参数模型要求方程中的变量是平稳的，或变量之间存在协整关系，因此，需要对变量进行单位根检验，检验结果见表1。

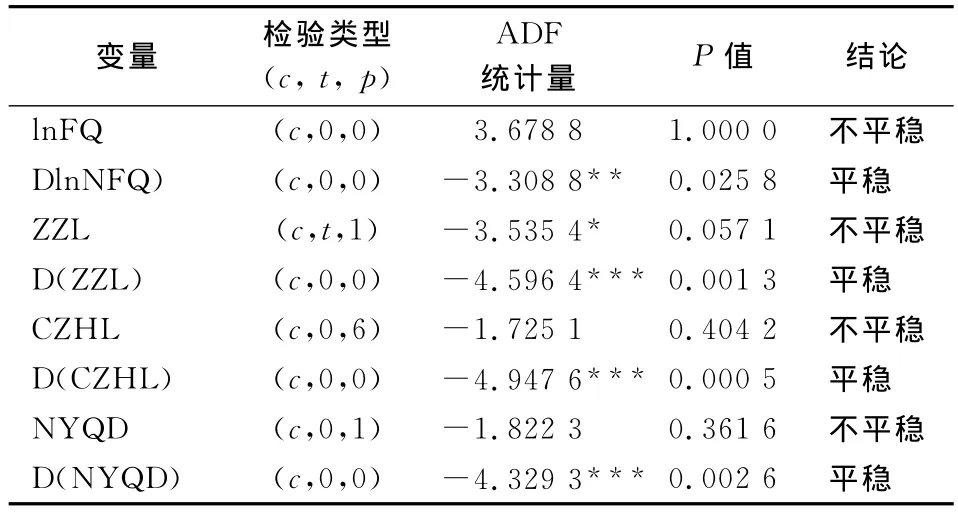
表1 变量的单位根检验结果表

由上表可知，lnFQ、ZZL、CZHL和NYQD四个变量均为一阶单整，符合建立协整关系的前提条件。另外，还需对变量间的协整关系进行Johansen检验，结果见表2。

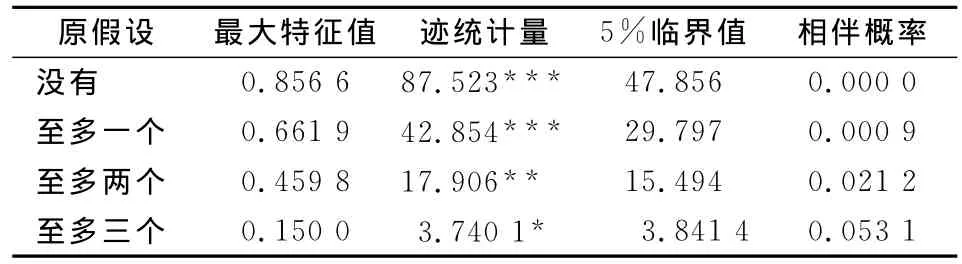
表2 变量的协整检验结果表

协整检验结果表明变量间存在协整关系，这样就避免伪回归，可以建立状态空间模型，进一步分析变量间的动态关系。

2．模型的估计结果与检验

根据式（1）和式（2）式中模型的设定，运用Eviews6．0对模型进行求解，得到状态空间模型的估计结果。

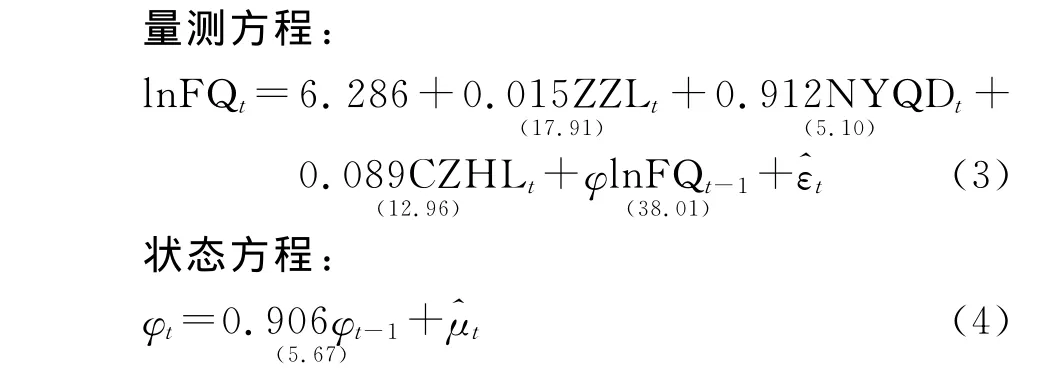
经检验，该模型R2＝0．997，残差的ADF单位根检验为平稳，不存在一阶自相关。

四、用线性规划模型求解环境约束下的经济增长率集合

（一）目标函数和约束条件

1．目标函数的建立

前面通过状态空间模型估计了废气与经济增长率的关系，根据计量模型的假定，在残差平稳的条件下，残差的均值是0，所以可以省略误差项，将估计的关系式作为确定性关系式应用，将其作为线性规划模型的目标函数。因为要求解的是最优经济增长率，所以将原状态空间方程经济增长率变量放到目标函数的左边，废气变量放到方程的右边，这样，就把原来的环境污染最小化问题，转化成经济增长率最大化问题。线性规划模型为：

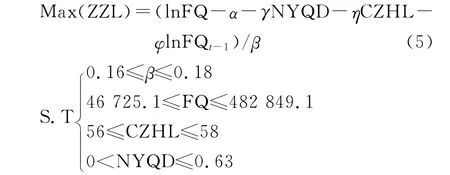
2．约束条件的确定

根据状态空间模型的变系数方程，可以约束方程中的系数，也可以约束目标方程中的变量。设计约束条件的指导思想是：国家有规划目标的，按国家规划目标测算；国家没有规划目标的，按理论标准或实际数据趋势划定约束界限，其中有的要设定上限值，有的则约束下限值。在本文的目标规划方程中，与经济增长率有关的变量除了废气排放量，还有能源强度、城镇化率以及经济增长率对废气排放量的弹性。下文对于废气排放量的约束是借鉴“十二五”规划目标值，其他变量也需要用与废气发展状态相对应的约束值才能求得环境约束下的最大经济增长率。因此，在该线性规划中，除了要对废气排放量进行约束，还需要对其他的有关变量进行约束。

废气排放约束：根据国家出台的《十二五规划》等一系列相关经济、环境政策文件，给出“十二五”期间具体的目标值，见表3。

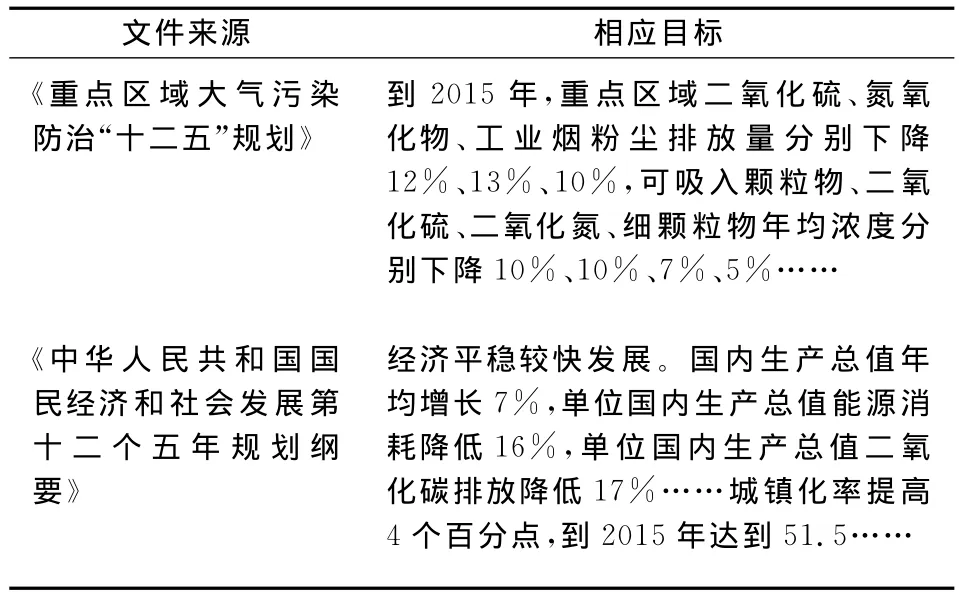
表3 “十二五”规划目标值表

《纲要》上并没有给出废气排放量约束的具体指标，而是给出了废气中二氧化硫、氮氧化物的约束指标，本文将全国二氧化硫的约束指标10%作为废气排放量下降的上限，将全国二氧化氮下降7%的约束指标作为废气排放量下降的下限，则现阶段废气排放量降幅的约束区间为［7%，10%］，对应具体废气排放量的区间为［467 251．2，482 849．1］。

城镇化率约束：《纲要》中要求到2015年达到51．5，考虑到2011年的中国城镇化率已经为51．3，通过由中国公布的数据计算得到近10年中国城镇化率的增长速度在2%～3%的范围，按照这个速度，到“十二五”末期，中国城镇化率的区间约束为［56，58］。

单位国内生产总值能源消耗约束：《纲要》中要求在2015年单位GDP能耗降低16%，按照2010年的GDP能耗下降16%得到0．63吨／万元，因此本文对GDP能耗进行约束时，要求其小于0．63吨／万元。考虑GDP能耗现阶段不可能为0，因此其下限一定大于0。

废气排放与经济增长率的弹性系数约束：弹性系数的求解，根据方程关系，可以推导出弹性系数公式为：

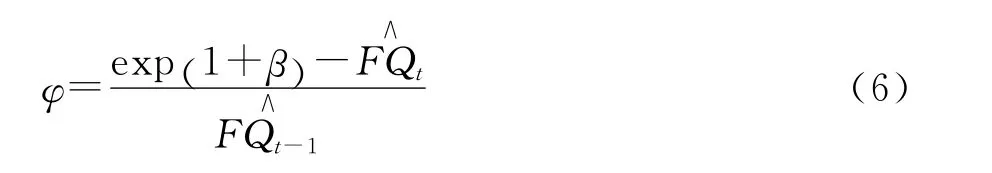
根据公式，可以算出经济增长率对工业废气排放总量增长率的弹性系数。计算结果表明：中国经济增长率与环境污染呈斜率不同的线性变动关系，并且该斜率的变化有一定的波动范围，取值区间为［0．18，0．27］，平均值为0．22。在2000年以前，弹性系数主要在0．20～0．22区间变动，2001年开始，弹性系数随时间呈线性增长趋势（除2008年经济危机有所降低外）。考虑到现阶段国家对于环保投资加大，淘汰高能耗产业以及科技进步等因素，该系数的上限现阶段不会超过0．18，同时考虑到其下降的速度不会太快，故本文设定其现阶段的下限为0．16。由此，确定了约束条件，对应到对数模型中经济增长率前的系数约束区间为［0．011 324，0．012 484］。

废气滞后系数平均化处理。由于方程中含有废气的滞后一期项，因此其系数原则上不能超过1，对应到对数模型中，其系数就不能大于0，虽然本文不对其做约束，但为了简化计算，对其做了平均化处理。考虑到这个系数变化并不是很大，取其之前所有系数的平均值（－0．004 54）作为目标方程废气排放量滞后一期项前的系数。

（二）适度经济增长率求解

1．求解多维约束条件下的最大经济增长率

依据不同的问题，线性规划的算法有所不同。通常情况下，线性规划的算法有图解法、单纯形算法、基线法（由于它们都是在可行集的边界上取得最优值，故合称为边界点算法）、内点法、椭球法及其各种改进算法。单纯形算法的基本原理是：先找出一个基可行解，判断其是否为最优解，如为否，则转换到相邻的基可行解，并使目标函数值不断增大，一直找到最优解为止。内点算法是针对单形法的“边界趋近”观念而改采“内部逼近”的路线，相对于只沿着可行域的边沿进行移动的单纯形算法，内点算法能够在可行域内移动，本文使用内点法进行求解。具体作法为：同时将各种约束的各种可能取值带入方程，得到各种组合条件下的经济增长率。

考虑到每一个约束条件都属于时点数据，并不连续，因此在求解时，只能选取每个条件中的一个数值，根据每个条件的区间范围，从每个条件中均选取10个点，在选取每个点时采取下列方法：在增长率前的系数β、城镇化率和废气排放量的选择上，都将其约束区间10等分，取其区间的上限点或者下限点。在能源强度的选择上，以0．63为起点，按照1%的下降速度分别求出9个点。因为废气排放量的滞后一期的数值与废气排放量是一一对应的，根据之前的废气排放量的数据，就可以求出其滞后一期的数值。最终选取符合各个条件的数值见表4。

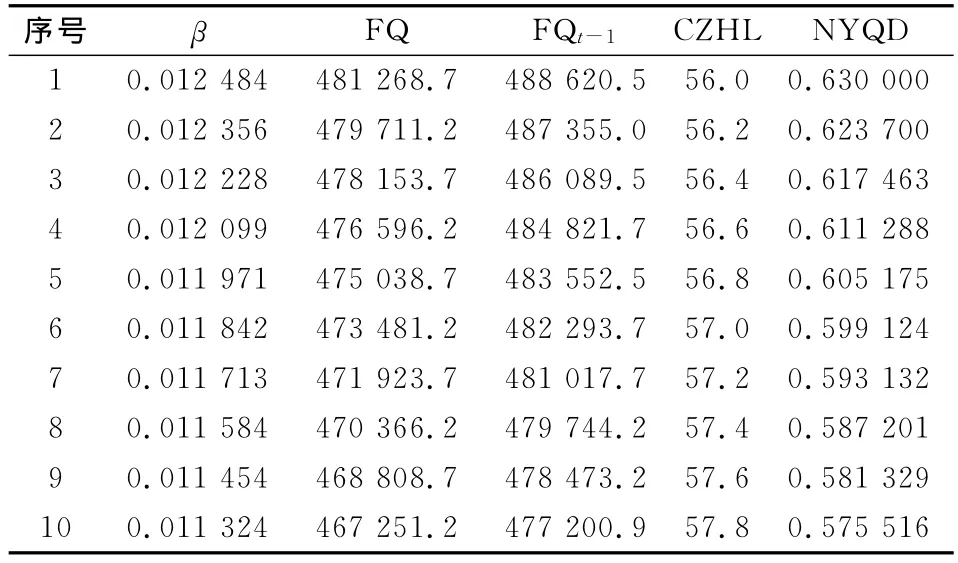
表4 各变量细分值表

上述四个变量都有10个细分点，每个细分点都带入目标方程中计算一次，最后共得到＝10 000个经济增长率的样本点。在这10 000个经济增长率样本点中最小值为89．72，最大值为120．03。

2．求解单项约束条件下的最大经济增长率

另一种方法是对四个约束条件分别进行约束，在其他条件固定的情况下考察单项约束下的经济增长率。最终分别求得四个约束条件下可能的经济增长率的区间。设Xi为某一约束变量，a与b分别为其约束的下限和上限，Y1、Y2、Y3分别为其余三个约束条件，k、h、f分别为三个约束取值范围中的一个固定点，则模型可以表达为：

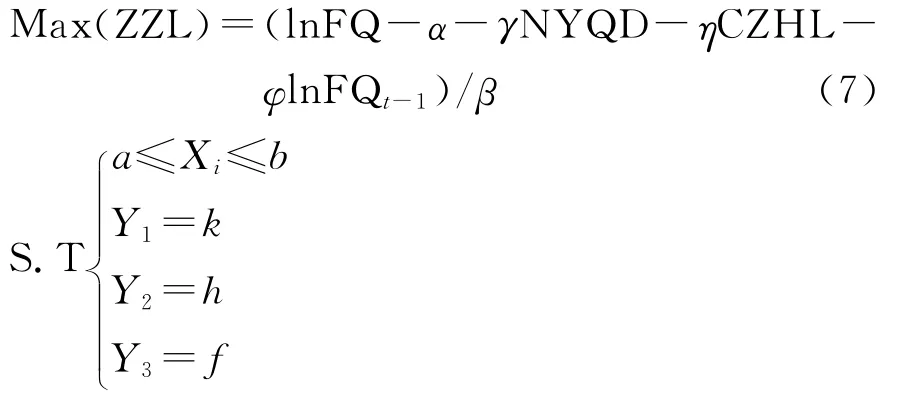
单项约束的具体做法是在研究某一约束条件时将其他条件固定不变，可以得出该约束条件的每一个取值所对应的经济增长率。例如，废气排放单项约束时，仅让废气约束变化，能源强度、城镇化率和弹性系数都固定在某一给定的点。对于其它约束的固定取值，确定为各自约束条件下接近于现状的上限或下限值。四个约束条件的固定取值见表5。

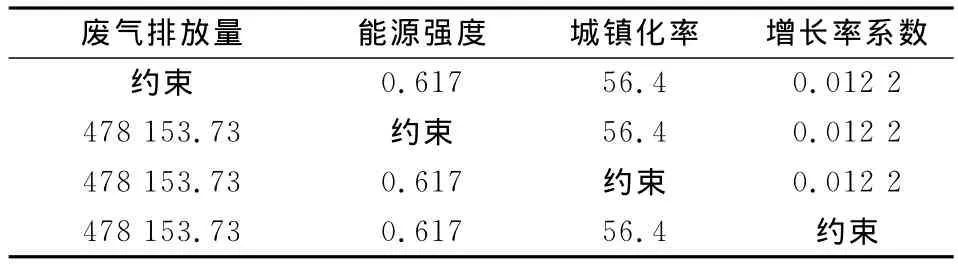
表5 四个约束条件的固定取值表

对此模型求解，可以得出每一个单项约束下可能的经济增长率集合与最大经济增长率，具体数值见表6。

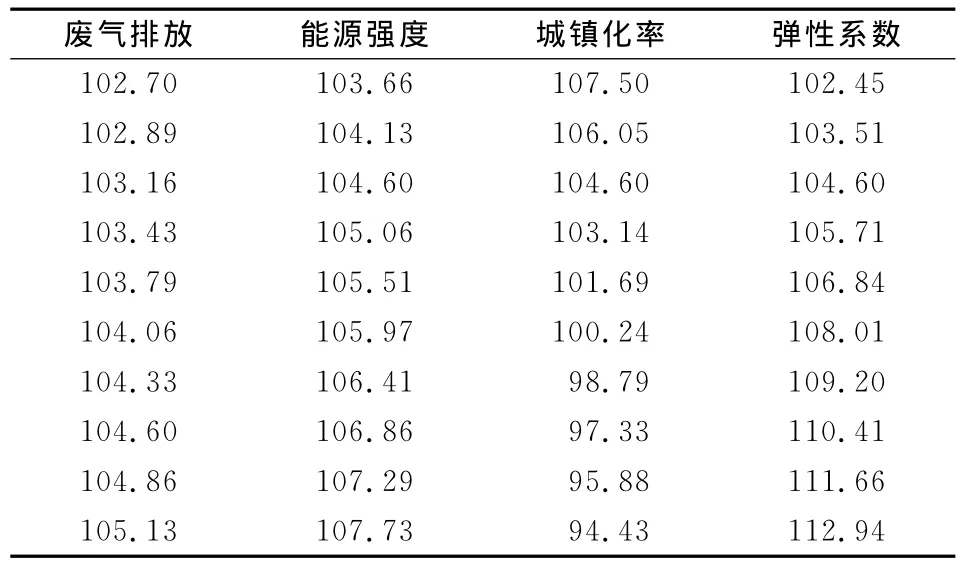
表6 单项约束下可能的经济增长率表

从表6可以看到，废气排放、能源强度、城镇化率、弹性系数各自约束下的最大经济增长率分别为105．13、107．73、107．50、112．94。

五、适度经济增长率的估计与选择

在现阶段，与中国的实际情况相结合，上文所求得的最大经济增长率要么太高，要么太低，并不是适合中国国情的环境约束下的适度经济增长率。在上文所求得的所有经济增长率集合中，我们使用两种方法来进行适度经济增长率区间的选取。

（一）多维约束下的适度经济增长率求解

多维约束下的适度经济增长率，是指在多维约束条件下求得的所有经济增长率的取值点中，样本密集分布区间的经济增长率。

上文在多维约束条件下，使用线性规划的方法求出了10 000个经济增长率的可能取值点并获取了最大值。但最大值不一定等于适度值，因为最大值和最小值，都是在各个约束变量取极端值时产生的，因此需要找到一种具有普遍适用性的规律。根据统计学大数定律，可以将数据密集区域，即围绕在均值周围的区域看做是符合普遍性的适度区域。图1展示了前面多维约束条件下产生的10 000个结果的统计分布。

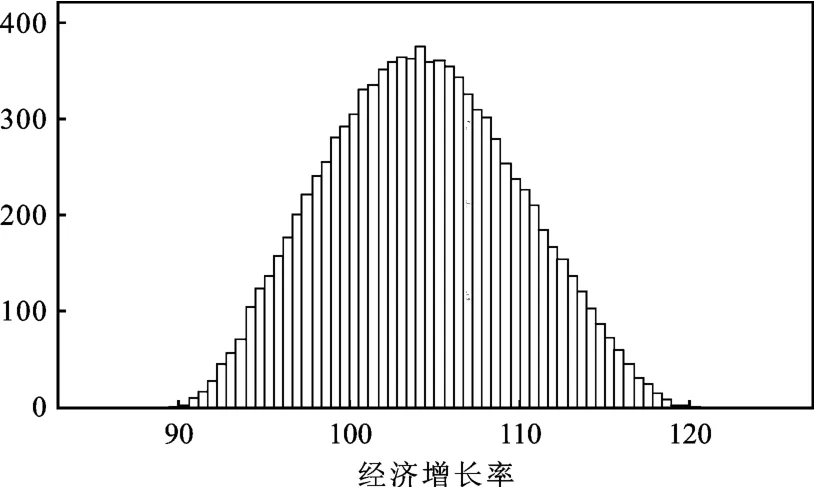
图1 多项约束下可能的经济增长率的概率分布

从分布图上直观可以看出，多维约束下得到的可能的经济增长率大致属于正态分布，所以可以在给出一定置信度的条件下，用正态分布的区间估计方法求出样本均值及其浮动范围作为适度增长率。为了判定其分布，需要计算其统计量，具体结果见表7。

表7 多项约束下经济增长速度分布的主要统计量表

从表7可以看出，样本的偏度为0．087接近于0，峰度为2．554接近3，考虑其样本量已经达到10 000，属于大样本，因此可以认为该总体已经近似服从正态分布。对于总体服从正态分布，均值和方差都未知的大样本，使用下述公式进行均值区间估计：

（二）单项约束下的最优经济增长率求解

现在换一种思路来求解适度经济增长率区间。在前面单项约束条件下，各自产生了10个经济增长率点，如果把这些点都汇集到一起，是否会有一些公共的因素呢？如果有公共交集部分，就可以将其看做同时符合各单项约束的适度经济增长率。这样就把问题转换成了将四个变量所对应的增长率所组成的集合求其交集问题。

通过上述计算可以得到，四个单项约束条件下的经济增长率的共同区域为［103．66，105．13］，见图2。

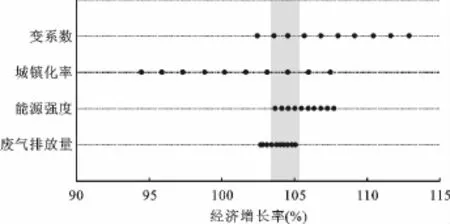
图2 单项约束下的共同经济增长率区间

六、研究结论

本文通过建立状态空间和目标规划模型，使用区间估计和集合求交集的方法，研究了环境约束下的适度经济增长率，得出如下结论：

1．根据状态空间计量模型估计结果，证明了环境与经济增长率是一种正向因果关系，经济增长率越高，环境污染将越大。这也证明了我们所提出的二者相克、相济共生的理论观点。

2．在环境约束下，存在一个经济增长率的极大值，在两种不同的方法测算下有不同的结果，多维约束条件下和单项条件约束下的极大值分别约为20%和13%。

3．环境约束下的极大值不一定是适度值，分别用正态分布区间估计和集合论求交集的两种方法测算的适度经济增长率都集中在4%左右，非常一致，将两种方法的共同信息都考虑进去，可以确定中国现阶段环境约束下的适度经济增长率区间在3%～5%范围。超过这个范围，可能就需要以牺牲环境为代价。

4．现阶段，中国不能单纯追求高经济增长率，而必须考虑环境约束，这些约束主要包括环境对经济增长的弹性系数约束、单位GDP能源消耗约束、城镇化速度约束和污染物排放约束。

［1］ Markus P．Technical Progress，Structural Change，and the Environmental Kuznets Curve［J］．Ecological Economics，2002，42（3）．

［2］ Dasgupta S，Laplante B，Wang H，et al．Confronting the Environmental Kuznets Curve［J］．The Journal of Economic Perspectives，2002，16（1）．

［3］ 胡宗义，刘亦文，唐伟杰．低碳经济背景下碳排放的库兹涅茨曲线研究［J］．统计研究，2013（2）．

［4］ Panayotou T．Economic Growth and the Environment［J］．Economic Survey of Europe，2003（2）．

［5］ 梅国平，万建香．环境约束下我国经济增长的内生机理——基于CDE与FBA的数理分析与数字校正［J］．经济管理，2012（3）．

［6］ 岳书敬，刘富华．环境约束下的经济增长效率及其影响因素［J］．数量经济技术经济研究，2009（5）．

Researching on Moderate Economic Growth under the Environmental Restriction in China：The Analysis Based on Exhaust Emissions

LI Bao-yu，LIU Yang
（School of Statistics，Shanxi University of Finance ＆ Economics，Taiyuan 030006，China）

The relationship between economic development and environmental pollution has always been one pair of unavoidable conflicts，which is also the academic research focus，the majority of domestic and foreign scholars have been paid their attention on the study of the environmental Kuznets curve，but the relationship between environment and economic growth always be ignored．In this paper，we firstly establish the time-varying parameter state space model of the relationship between environment and economic growth，and transformed the time-varying parameter state space model into a decision-making equation of linear programming，and then we apply the methods of interval estimation of parameters and set theory to estimate China＇s current optimal economic growth under the environmental constraints by constraining the variables and coefficient．At last we get the range of optimal economic growth which is between 3%and 5%．

moderate economic growth；environmental restriction；state space model；linear programming model

F205

A

1007－3116（2014）04－0023－07

2013－11－15；修复日期：2014－01－17

李宝瑜，男，山西文水人，教授，博士生导师，研究方向：国民经济核算与宏观经济统计分析；

刘 洋，女，山西介休人，硕士生，研究方向：国民经济核算与宏观经济统计分析。

（责任编辑：张治国）