基于核和灰度的灰色异构数据代数运算法则及其应用

曾 波，孟 伟，熊 遥

（重庆工商大学a．商务策划学院；b．电子商务及供应链系统重庆市重点实验室；c．长江上游经济研究中心，重庆 400067）

基于核和灰度的灰色异构数据代数运算法则及其应用

曾 波a，b，孟 伟a，b，熊 遥c

（重庆工商大学a．商务策划学院；b．电子商务及供应链系统重庆市重点实验室；c．长江上游经济研究中心，重庆 400067）

为解决灰色异构数据的建模问题，应用“核和灰度”对灰色异构数据代数运算法则及其性质展开研究。将灰信息表征为“核和灰度”，通过“核”将灰色异构数据代数运算转换为实数之间代数运算，根据灰度不减公理确定运算结果之灰度，在此基础上构建灰色异构数据的代数运算法则，并将该法则应用于灰色异构数据预测模型的构建及空气质量指数（AQI）的预测。研究成果对丰富与完善灰色系统基础理论具有积极意义。

灰色理论；代数运算法则；灰色异构数据；核和灰度；

一、引 言

1982年中国著名学者邓聚龙基于“灰箱”思想创立了灰色系统理论，并被广泛应用于工业、农业、医学、军事等领域［1－3］。灰色系统用灰数、灰色方程、灰色矩阵等来描述，其中灰数是灰色系统的基本“单元”或“细胞”，主要包括区间灰数及离散灰数等［4］；灰数之间的代数运算是构建灰色系统模型的基础，刘思峰较早对灰数运算法则进行了研究，提出了灰数均值白化数的概念，并以此为基础构建新的灰数运算体系，但由于难以处理令人棘手的扰动灰元而无果，之后刘思峰试图通过借鉴区间数的研究方法来构建区间灰数运算体系，但由于前者同样存在若干问题而一直争议较多；方志耕等人定义了第一和第二标准区间灰数的运算，设计了普通区间灰数与标准区间灰数之间的转换规则，构建了标准区间灰数之间的比较与运算法则体系，这对解决区间灰数之间的大小比较与运算问题的解决起到了一定的推动作用，但该方法的运算工作量随着运算复杂程度的增加而呈快速递增的趋势，在一定量的运算复杂程度下该方法的适用性较差［5］；刘思峰等人又给出了区间灰数“核”的定义，并基于“核”和灰数灰度建立了区间灰数运算公理和灰数运算法则［6］。至此，灰数之间的代数运算被化为实数运算，区间灰数之间的运算问题在一定程度上得到了解决。

上述灰数之间的代数运算均在同构数据之间进行，如区间灰数之间、标准离散灰数之间，而对于具有不同数据类型的灰色异构数据（如区间灰数与离散灰数）之间尚无有效的代数运算规则，因为难以知道一个区间灰数与一个离散灰数之间的运算结果究竟应该是什么类型的灰数［7］。尽管灰色异构数据具有不同的数据结构及灰信息特征，但均同属“灰数”范畴，都具有“核”和“灰度”这一基本的共同属性，因此可以利用“核”和“灰度”来研究灰色异构数据之间的代数运算法则，通过“核”将灰色异构数据之间的代数运算转化为实数运算，这在一定程度上解决了灰色异构数据之间运算难题，为灰色异构数据建模提供理论支撑，对丰富与完善灰色系统理论体系和拓展灰色模型适用范围具有积极意义。

二、定义及公理

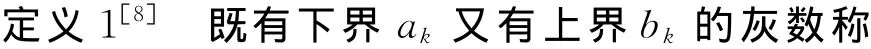
公理1［6］（灰度不减公理）两个灰度不同的区间灰数进行和、差、积、商运算时，运算结果的灰度不小于灰度较大的区间灰数之灰度。

因此，通常可将灰色异构数据之间运算结果的灰度取为灰度较大的区间灰数的灰度。由公理1不难得到如下推论：

推论1［6］一个白数与一个区间灰数进行和、差、积、商运算时，运算结果的灰度与区间灰数的灰度相同。

推论2 对具有相同论域的灰色异构数据之间进行“和、差、积、商”运算时，运算结果的信息域不小于灰色异构数据中最大灰度所对应灰数之信息域。

根据公理1及灰度的定义可知，推论1和推论2显然成立，证明略；根据推论1及推论2可知，当若干个灰色异构数据进行运算时，首先对“核”作相应运算，然后按照取大准则得到运算结果的灰度或信息域，从而可得运算结果的简化形式［13］。

三、灰信息“核”与“灰度”的计算

（一）灰信息“核”的计算

（二）灰信息“灰度”的计算

灰数的灰度反映了人们对灰色系统认识的不确定程度。游中胜等人对区间灰数灰度的计算方法进行了拓展研究［15］，即：

四、灰色异构数据代数运算法则

灰色异构数据（区间灰数、离散灰数、实数或其他灰信息）虽然具有不同的数据结构及灰信息特征，但均同属“灰数”范畴（实数是灰度为“0”的特殊灰数），都具有“核”和“灰度”这一基本的共同属性，因此可以通过“核”和“灰度”来研究灰色异构数据之间的代数运算法则。显然，灰色异构数据之间进行加、减、乘、除、开方以及矩阵等运算之后，其运算结果自然也是灰数。因此，将灰色异构数据转换为“核”与“灰度”，然后在此基础上研究基于核和灰度的灰色异构数据之间的代数运算方法。

当参与运算的灰元均为区间灰数，则其和、差、积、商等运算是法则1～6的特列，即刘思峰所讨论的区间灰数运算法则。因此，本文所研究的灰色异构数据代数运算法则是在其基础上的推广与拓展。

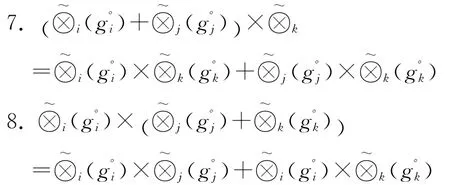
五、空气质量指数（AQI）预测

2013年初以来，中国发生了大范围持续雾霾天气。据统计，受雾霾影响区域包括华北平原、黄淮、江淮、江汉、江南、华南北部等地区，受影响面积约占国土面积的1／4，受影响人口约6亿人。雾霾是一种灾害性天气，对公路、铁路、航空、航运、供电系统、农作物生长等均产生重要影响，同时雾霾会造成空气质量下降，影响生态环境，给人体健康带来较大危害。AQI（Air Quality Index，空气质量指数）是表征空气质量的重要参数，描述了空气清洁或者污染程度以及对健康的影响。环保部门通过收集、分析、汇总分布在城市各个典型区域空气监测点的观测数据，整理形成该城市的AQI指数，由于数据处理过程的不确定性并最终导致了灰色异构时序数据的产生（因版面所限，图省略）。

重庆2013年12月2日至12月6日的空气质量指数如表1所示。试应用本文研究成果，构建基于灰色异构时序数据的重庆空气质量指数灰色预测模型，并根据该模型对重庆2013年12月7日至11日的AQI指数进行预测（表1中数据的“核”信息来自PM2．5监测网）。

表1 重庆2013年12月空气质量指数个表

根据式（11）可计算模型的模拟误差，见表2。

表2 灰色异构数据“核”序列的模拟值与模拟误差表

步骤5 模型误差检验。

根据表2中的数据，可对式（11）所模拟的数据分别进行平均相对误差检验和灰色关联度检验，并对模型的模拟结果进行精度等级评价。

1．平均相对误差检验

3．误差检验结论

根据空气质量指数（AQI）的灰色异构数据预测模型（11），可得当k＝6，7，8，9．10时重庆2013年12月7日—12日的AQI预测值，如表3所示。

表3 重庆2013年12月空气质量指数预测值表

从表3不难看出，重庆2013年12月空气质量指数呈现不断下降的趋势，表明重庆空气质量将持续好转。预测结果对重庆市环保部门研究和制定空气质量环保措施具有一定的参考价值与借鉴意义。

六、结 论

本文应用“核和灰度”对灰色异构数据代数运算法则及其性质展开研究，并在此基础上构建空气质量指数（AQI）的灰色异构数据预测模型，研究成果对丰富与完善灰色系统基础理论、拓展灰色系统模型的应用范围、促进灰色系统模型与现实问题的有效融合，均具有积极意义。如何基于灰色异构数据序列构建灰色关联模型与灰色决策模型以及多变量灰色异构数据预测模型等内容，将是本项目团队下一步研究的主要内容。

［1］ Deng Julong．Introduction to Grey System Theory［J］．The Journal of Grey System （UK），1989（1）．

［2］ 范德成，张伟．基于灰色变结构控制的中国产业结构优化模型及分析研究［J］．统计与信息论坛，2010（10）．

［3］ 刘秋华，陈洁，甘海庆．基于改进灰色模型的售电量预测分析［J］．统计与信息论坛，2009（11）．

［4］ Liu Sifeng，Lin Yi．On Measures of Information Content of Grey Numbers［J］．Kybernetes：The International Journal of Systems ＆Cybernetics，2006（5）．

［5］ 方志耕，刘思峰．基于区间灰数序列的 GM（1，1）模型（GMBIGN（1，1）研究［J］．中国工程科学，2005（2）．

［6］ 刘思峰，方志耕，谢乃明．基于核和灰度的区间灰数运算法则［J］．系统工程与电子技术，2010（2）．

［7］ 曾波．基于核和灰度的双重异构数据序列预测建模方法研究［J］．统计与信息论坛，2013（10）．

［8］ 杨德岭，刘思峰，曾波．基于核和信息域的区间灰数Verhulst模型［J］．控制与决策，2013（2）．

［9］ Liu Sifeng，Liu Yi．Grey Systems Theory and Applicationg［M］．Berlin Heidelberg：Springer-Cerlag，2010．

［10］Deng Julong．Whitening Definitions in Grey System Theory［J］．The Journal of Grey System，1998（2）．

［11］Liu Sifeng．On Measure of Grey Information［J］．The Journal of Grey System，1995（2）．

［12］曾波，刘思峰，李川，等．基于蛛网面积的区间灰数灰靶决策模型［J］．系统工程与电子技术，2013（10）．

［13］曾波．基于核和灰度的区间灰数预测模型［J］．系统工程与电子技术，2011（4）．

［14］Zeng Bo，Liu Sifeng．Calculation for Kernel of Interval Grey Number Based on Barycenter Approach［J］．Transaction of Nanjing University of Aeronautics ＆ Astronautics，2013（2）．

［15］You Zhongsheng，Zeng Bo．Calculation Method’s Extension of Grey Degree Based on the Area Method［J］．The Journal of Grey System，2012（1）．

［16］Xie Naiming，Liu Sifeng．Discrete Grey Forecasting Model and Its Optimization［J］．Applied Mathematical Modeling，2009（1）．

［17］刘思峰，党耀国，方志耕，等．灰色系统理论及其应用［M］．5版．北京：科学出版社，2010．

Algebra Algorithm Rules of Grey Isomerism Data Based on Kernel and Grey Degree and Its Applications

ZENG Boa，b，MENG Weia，b，XIONG Yaoc
（a．Strategical Planning College；b．Chongqing Key Laboratory of Electronic Commerce and Supply Chain System；c．Research Center of the Economy of the Upper Reaches of the Yangtze River，Chongqing Technology and Business University，Chongqing 400067，China）

In order to solve the modeling problem of grey isomerism data，this paper applies＇kernel and grey degree to study the algebra algorithm rules of grey isomerism data and its properties．Grey information is represented as kernel and grey degree，and the algebra algorithm is switched from grey isomerism data to real numbers through kernel．The grey degree of calculation result is defined by the axiom of grey degree not-reducing；on those basses the algebra algorithm rules of grey isomerism data is established．Finally，this paper employs the novel algorithm rules to build a prediction model of grey isomerism data sequence and forecast the air quality index （AQI）．The research findings have a positive significance for enriching and perfecting the basic theory of grey system．

grey theory；algebra algorithm rules；grey isomerism data；kernel and grey degree

N941．5∶O213．9

A

1007－3116（2014）04－0018－06

2013－06－24；修复日期：2014－01－09

重庆工商大学青年博士基金项目《灰色多源异构数据预测模型构建研究》（1152003）

曾 波，男，四川威远人，系统工程博士，副教授，研究方向：系统预测、决策与评价；

孟 伟，男，湖北荆门人，博士生，副教授，研究方向：灰色理论及商务智能；

熊 遥，女，重庆梁平人，硕士生，研究方向：区域经济理论与政策。

（责任编辑：郭诗梦）