求解灰色Verhulst模型参数的新方法

高彦琴，魏 勇

（西华师范大学 数学与信息学院，四川 南充 637002）

求解灰色Verhulst模型参数的新方法

高彦琴，魏 勇

（西华师范大学 数学与信息学院，四川 南充 637002）

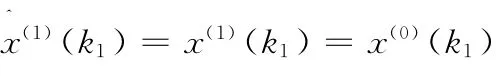
灰色Verhulst模型；灰色微分方程；参数求解；最小二乘法

一、引 言

灰色系统模型是通过累加生成序列的随机性，寻找系统变化规律，经过定性分析建立模型，通常具有较高的模拟和预测精度，可以得到较好地应用效果［1］123－126。对于数据呈S型的序列，通常适合灰色Verhulst模型进行建模预测，灰色Verhulst模型具有小样本下特定优势，在适用范围方面优于传统的Verhulst模型，因此，近年来该模型得到了广泛的应用［2－4］。熊萍萍等优化了等间距灰色Verhulst模型的背景值，取得较原模型更高的模拟预测精度［5］。王正新等对非奇次指数函数作导数生成，构建无偏灰色Verhulst模型，取得较好的模拟预测效果［6］。戴文战通过优化结构参数估计法和重构背景值，构建了改进的灰色Verhulst模型［7］。针对非等间距的灰色Verhulst模型的预测应用问题也有学者进行研究。偶昌宝等通过在区间上求积分改进了非等时距Verhulst模型的背景值计算公式，实现了对沉降量的预测［8］。韩朝晖等研究了非等间距Verhulst直接模型，实现了在装载机销售量中的预测［9］。Hu Wei等通过增加系数项优化背景值，实现了未来网络安全形势的预测［10］。张宏斌等研究了非等时距Verhulst修正模 型，对 直 升 机 累 计 故 障 率 进 行 预 测［11］。Xiong Pingping等建立了时间响应函数优化的非等间距Verhulst模型，并取得了较原模型更高的模拟预测精度［12］。本文改变“通过代入初始条件（1）（k1）＝x（1）（k1）＝x（0）（k1）整理求解α，β”的传统方法为“通过灰色微分方程利用最小二乘法确定α，β”新方法，对灰色Verhulst模型的建模方法进行改进，并通过等间距与非等间距的实例，将传统模型及近期一些优化模型对比分析，说明了新方法的可行性和优越性。

二、传统灰色Verhulst模型的建模方法

（一）基本概念

设时间序列为K＝ ｛k1，k2，…，kn｝，其对应原始数据序列为：

（二）传统灰色Verhulst模型的建模方法

三、优化的灰色Verhulst模型的建模过程

四、实例比较分析

（一）等间距灰色Verhulst模型的建模方法比较分析

例1中国2002—2009年天然原油生产量数据如表1［7］。

表1 中国2002—2009年天然原油生产量数据 单位：亿吨

观察表1中的监测数据可以发现，此组数据本身呈S型的形态，这时可以取原始数据为X（1）（ki），不经过一阶累加生成本文的灰色Verhulst模型。

通过式（3），解得a＝－0．199 1。通过式（6）解得α＝0．011 1，β＝0．049 5。从而可得原始序列模拟预测公式：

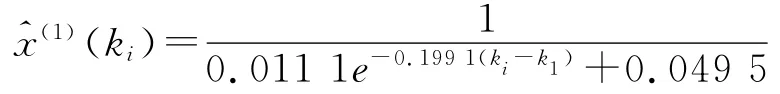
传统方法与改进Verhulst模型的方法及本文方法的计算结果比较见表2。

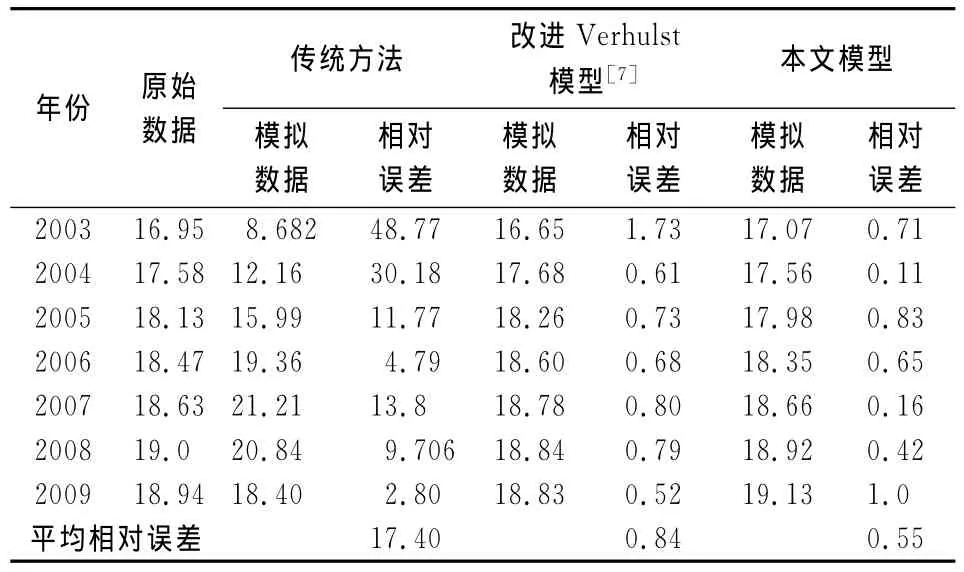
表2 原始数据与各种预测数据的比较

由表2可以看出本文方法构建的灰色Verhulst模型的平均相对误差最小，为0．55%，传统方法构建的等间距灰色Verhulst模型的平均相对误差最大，为17．40%，改进Verhulst模型的平均相对误差居中，为0．84%。本文方法不仅误差小，而且参数估计的计算过程比其他方法简单。

（二）非等间距灰色Verhulst模型的建模方法比较分析

例2某型直升机累计故障率数据见表3［11］。

表3 某型直升机累计故障率数据

观察表3中的数据可以发现，此组数据本身呈S型形态，这时可以取原始数据为X（1）（ki），不经过一阶累加生成本文灰色Verhulst模型。

传统方法、增加预测误差修正项的方法与本文方法的非等间距Verhulst模型的计算结果比较见表4。

由表4可以看出本文构建的灰色Verhulst模型的平均相对误差最小，为4．70%，传统方法构建的非等间距灰色Verhulst模型的平均相对误差最大，为7．34%，非等间距Verhulst修正模型平均相对误差居中，为6．86%。

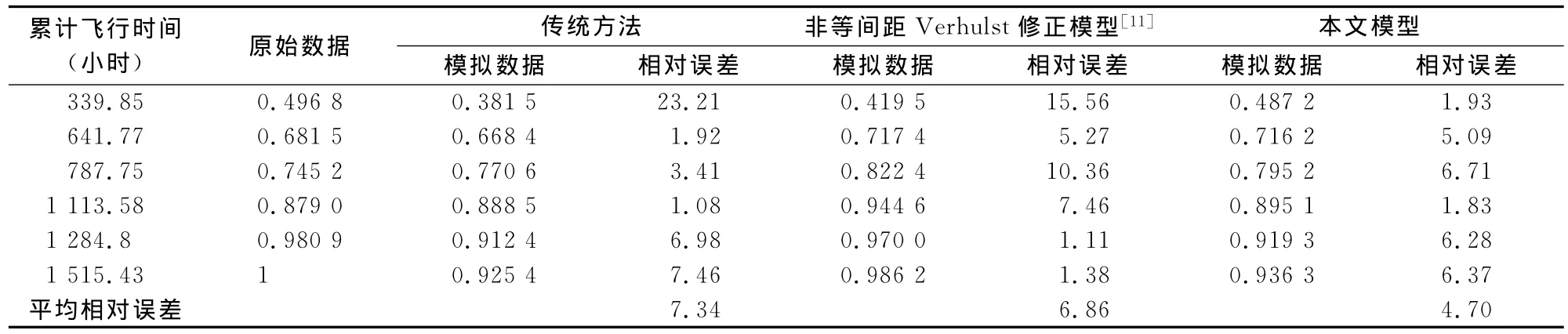
表4 原始数据与各种预测数据的比较

五、结束语

本文所举实例不仅说明本文方法的可行性，也说明了本文方法既适合等间距，又适合于非等间距。与传统模型比较，该方法大幅度提高了预测精度。

［1］ 刘思峰，党耀国，方志耕．灰色系统理论及其应用［M］．北京：科学出版社，2004．

［2］ 罗战友，龚晓南，杨晓军．全过程沉降量的灰色Verhulst预测方法［J］．水利学报，2003（3）．

［3］ 张伏生，刘芳，赵文彬．灰色 Verhulst模型在中长期负荷预测中的应用［J］．电网技术，2003，27（5）．

［4］ 刘峰．基于灰色 Verhulst模型对边坡变形预测研究［J］．公路工程，2013，38（4）．

［5］ 熊萍萍，党耀国，姚天祥，等．灰色Verhulst模型背景值优化的建模方法研究［J］．中国管理科学，2012，20（6）．

［6］ 王正新，党耀国，刘思峰．无偏灰色 Verhulst模型及其应用［J］．系统工程理论与实践，2009，29（10）．

［7］ 戴文战，熊伟，杨爱萍．灰色 Verhulst模型的改进及其应用［J］．化工学报，2010，61（8）．

［8］ 偶昌宝，俞亚南，王战国．不等时距灰色Verhulst模型及其在沉降预测中的应用［J］．江南大学学报：自然科学版，2005（1）．

［9］ 韩朝晖，董湘怀．装载机销售量的非等间距Verhulst直接模型研究［J］．湖南师范大学自然科学学报，2008，31（2）．

［10］Hu Wei，Li Jianhua，Chen Xiuzhen，etc．Network Security Situation Prediction Based on Improved Adaptive Grey Verhulst Model［J］．Journal of Shanghai Jiaotong University，2010，15（4）．

［11］张宏斌，曹学峰，孙世霞．非等时距Verhulst修正模型及其在直升机故障率预测中的应用［J］．直升机技术，2012，173（4）．

［12］Xiong Pingping，Dang Yaoguo，Qian Wuyong．The Optimization of Time Response Function in Non-Equidistant Verhulst Model［J］．The Journal of Grey System，2010，22（3）．

New Method of Solving Parameters in Grey Verhulst Model

GAO Yan-qin，WEI Yong
（Mathematics and Information Institute，China West Normal University，Nanchong 637002，China）

grey Verhulst model；grey differential equation；solving parameters；the least square method

N941．5

A

1007－3116（2014）04－0014－04

2013－11－16

四川省应用基础研究资助项目《灰预测与灰决策量化方法及应用研究》（2008JY0112）；四川省高等教育人才培养质量和教学改革资助项目《灰预测与灰决策课程教学内容体系改革与教法探索》（P09264）；四川省留学人员科技活动择优资助项目《预测与决策方法及应用研究》（川人社函2010年32号）

高彦琴，女，山西吕梁人，硕士生，研究方向：灰色系统理论；

魏 勇，男，重庆丰都人，工学博士，教授，硕士生导师，研究方向：灰色系统理论。

（责任编辑：李 勤）