基于Copula函数的金融时间序列模型述评

张超锋，张莉敏

（1．对外经济贸易大学 国际经济贸易学院，北京 100029；2．四川文理学院 数学与财经学院，四川 达州 635000）

基于Copula函数的金融时间序列模型述评

张超锋1，2，张莉敏2

（1．对外经济贸易大学 国际经济贸易学院，北京 100029；2．四川文理学院 数学与财经学院，四川 达州 635000）

结合当前Copula函数及其应用的热点问题，着重评述了基于Copula函数的金融时间序列模型的应用。鉴于利用Copula可以将边际分布和变量间的相依结构分开来研究这一优良性质，在设定和估计模型时便显得极为方便和灵活。从模型的构造、Copula函数的选择、模型的估计以及拟合优度检验等几方面展开阐述和评价，介绍了Copula模型在金融领域中的几类应用，并对Copula理论和应用的新视角进行了展望。

Copula函数；相依结构；金融时间序列

一、引 言

在金融市场中，资产定价、投资组合、溢出效应、风险管理等问题都涉及相关性分析。线性相关系数，作为传统的相关性分析手段，由于其计算简单在实践中得到广泛应用。但是，线性相关系数要求变量间的关系是线性且方差为有限，在实际应用中往往得不到满足，例如金融市场中不少数据表现出厚尾特征，有些时候方差还根本不存在，因此用线性相关系数来刻画相关性存在很大的问题。只有当变量的联合分布服从椭圆分布如二元正态分布时，联合分布才能由变量间的相关系数和边缘分布唯一确定。为了克服传统的相关性统计分析的不足，最早由Skar提出的Copula理论表现出极大的优越性，并在金融领域中被广泛采用。首先，Copula函数不限制边缘分布的选择，可运用构造灵活的多元分布；其次，在建立模型时，可将随机变量的边缘分布和它们之间的相关结构分开来研究，其中它们的相依结构可由一个Copula函数来描述，这使建模问题大大简化并易于理解。另外，如果对变量作非线性的单调增变换，线性相关系数的值会发生改变，而由Copula函数导出的一致性和相依性测度的值则不会改变，因此由Copula函数导出的一致性和相依性测度应用范围更广、实用性更强。

随着计算机技术的快速发展，Copula理论在近十几年来得以迅速发展并成为金融领域的主要分析工具。目前国内有关Copula函数的研究基本局限于实证方面，在应用和理论方面都缺乏深层次的分析。鉴于此，本文对Copula理论与应用近几年新的研究进展进行系统的梳理，客观评价相应研究的可行性和局限性，结合最新文献试图提出一些进一步可拓展和思考的方向。

二、模型的构造

目前，运用Copula理论及其应用的范围涉及多个领域，研究的视角也存在很大差异，但有关Copula函数涉及的主要问题是函数形式和估计方法。Embrechts等对不同Copula函数模型进行了比较研究，发现采用不同形式的Copula函数可能导致完全不同的分析结果［1］。虽然Embrechts等曾就Copula函数的选择问题提出了相应的建议，但这一问题并未得到很好的解决。在实际操作中Copula函数的选择在很大程度上依赖于样本数据的特征和拟合优度检验。

为便于下文叙述，先给出Copula函数的定义和重要的Skar定理。更多相关概念可以参看Nelsen对Copula理论的介绍［2］7－24。本文限于篇幅，不再详细赘述。

如果F1，F2，…，Fd均为连续函数，则存在唯一的Copula函数使得上述等式成立。相反地，如果C是一个Copula函数并且F1，F2，…，Fd是一元累积分布函数，则上述等式所决定的函数F是F1，F2，…，Fd的联合分布函数。

由Skar定理立即可得：

Skar定理的重要作用在于通过Copula函数将边际分布函数巧妙结合，使得研究者在考察多个随机变量的联合分布时，可以将其分解为Copula函数和多个单变量分布函数来考虑整个联合分布的相关结构，从而解决了由随机向量边缘分布难以推导出联合分布的难题，为多元统计分析提供了一种便捷的新方法。

众所周知，金融时间序列的条件分布呈现时变波动、波动聚集、偏斜厚尾等特征，通常采用GARCH类模型以及随机波动率模型来描述这些特征。然而，由于金融市场之间的相关关系变化受各种因素的干扰而呈现出一定的复杂性，使得有时在估计这些模型参数时存在极大的技术困难。将Copula函数和这些模型结合到一起便能很容易地捕捉到时间序列之间的动态相依结构，常见的Copula函数的时间序列模型有Copula－GARCH模型、Copula－SV模型、时变Copula模型、RS－Copula模型等。Copula－GARCH模型中的GARCH描述的是各变量的条件边际分布，Copula函数刻画的是变量之间的条件相关关系。对上述模型进行适当调整，便可以描述金融市场波动的不同特征，比如波动的非对称性、波动的持续性等。与GARCH模型不同，随机波动率模型（SV）中的波动特征是由一个潜在的随机过程来描述的。在实际应用中，SV模型具有厚尾性，因为对于那些表现出明显的尖峰厚尾特征的数据序列，用Copula－SV模型能够更好地捕捉到时间序列之间的相依结构。Copula－GARCH模型和Copula－SV模型虽然能够很好地描述时间序列的统计特征，在考察序列之间的相依结构时也具有比较强的灵活性，然而却假定相依参数不会随时间变化而变化。事实上，金融市场本身会随着国家宏观经济政策的调整、外部市场环境的变化而变化，也就是说，金融市场间的相依结构可能会随时间的推移而发生改变，因而金融市场间相关系数也会随时间变化，Engle通过实证研究验证了这一事实［3］。进一步可以肯定用来研究随机变量间的非线性相依结构的Copula函数中相依参数也会表现出时变特征。很自然的一个问题便是如何确定时变Copula中的参数随时间变化的演化方程。Patton提出基于时变Copula相依结构的多元时间序列模型，类似于Copula－GARCH 模型［4－5］。不同的是，Copula函数中的时变参数服从一设定的动态方程。如果使用正态Copula描述变量间的相依关系，则时变Copula参数ρt服从下面的动态方程：

其中Λ2（x）是一个变换，确保相依参数总是能够落到其值域中去，对于尾部相依来说，Λ2（x）＝（1＋exp （－ x ） ）－1；对 于 Clayton Copula 来 说，Λ2（x）＝exp（x）；对于Gumbel Copula而言，Λ2（x）＝1＋exp（）x。金融市场中许多实证结果表明，收益率与交易量间具有明显的尾部相依性并且上下尾部具有不对称性。为了既可以刻画极端市场条件下收益间的尾部相依性，又能兼顾考察时变特征，Garcia等引入了RS－Copula模型（Regime－Switching Copula），以便刻画尾部相依性的动态特征以及结构突变［6］。尾部相依关系衡量了异常事件发生时序列间的极值联动关系。在几种常用的Copula函数中，高斯Copula的尾部相依性为0；Student－t Copula的上下尾部对称；Clayton Copula和Survival Gumbel Copula可用来描述下尾部相依关系，而Gumbel Copula和Survival Clayton Copula可用来描述上尾部相依关系。对于上述不同的Copula函数，可以使用AIC和BIC准则选择最优的Copula函数以刻画尾部相依特征，当Copula函数的密度函数已知的情况下，不必对原始数据做任何变换，采用贝叶斯理论的MCMC方法并基于DIC准则来估计Copula函数［7］。

三、Copula模型的选择

上文在构造模型时，所强调的只是对边缘分布的刻画，并没有对Copula函数的具体形式给出说明，然而Copula函数族中有很多函数类型，不同的Copula函数对变量间的相关结构的刻画各有所长，因此有必要对Copula函数的选择标准给予介绍。本文的目的当然是选择达到最优拟合效果的Copula函数，能够有能力捕捉到具有时变特征的相依过程。

Copula函数中的相依参数与几种重要的一致性相关性指标，如Kendallτ、Spearmanρ等常常有一一对应的关系，因此通过这些传统的一致性和相关性指标，使不同的Copula函数之间具有了可比性。为了更深入地探讨以上几种Copula函数的分布特性，图1中给出了几种常见的Copula函数的分布密度图［6］（其中秩相关系数τ＝3）。

从以上列举的几个Copula函数可以看出，不同Copula函数在描述相依结构时显示出明显差异。二元Gaussian Copula分布具有对称性，可以用来描述具有对称性的相依结构，却无法捕捉分布尾部相关性的变化，而具有同样对称结构的Frank Copula函数则更能捕捉到分布尾部相关性的变化。Gumbel和Clayton Copula函数可以用来描述变量间非对称的相依结构，Gumbel Copula函数在捕捉上尾相依结构时具有优势，而Clayton Copula函数则侧重于捕捉变量间下尾相依结构。然而金融市场千变万化，实践中很难用一种Copula函数就能很好地刻画市场间的相依关系，从而股票市场间的相关性都增大，比如说一般情况下股票市场出现暴跌或暴涨时市场间的相依关系都会明显增强并且通常上下尾部表现出非对称的特征，在这种情况下，用一种函数来刻画金融市场间的相依结构，只能反映金融市场之间相依结构变化的一种特征。很自然的想法是可以选用由 Gaussian、Frank、Gumbel、Clayton、Gumbel Survival Copula等其中若干种函数的线性组合构造的混合Copula（M－Copula）函数来刻画市场间的相依结构。图2给出了Gaussian（C1）、Gumbel（C2）和Survival Gumbel Copula（C3）三种函数在三种不同权重组合下的混合函数轮廓图。组合1：w1＝0．5，w2＝0；组合2：w1＝w2＝1／3；组合3：w1＝0，w2＝0．5，其中 M－Copula表达式为：

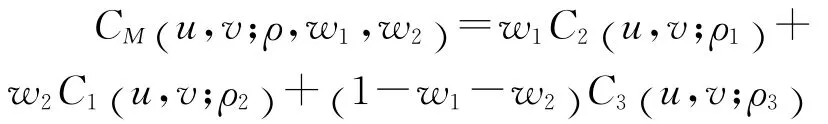
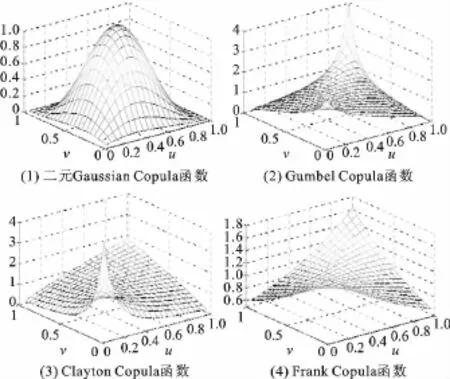
图1 几种Copula函数密度分布图

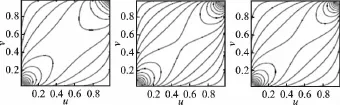
图2 三种组合下混合Copula函数密度轮廓图

事实上，M－Copula函数不仅可以涵盖它所包含的各种Copula函数的特性，而且通过选择不同权重系数组合还可以构造这些Copula函数的各种线性组合的混合特性。在实际应用中可以考虑选取一组权重系数用一个M－Copula函数来描述具有各种相依结构的金融市场间的关系，以便能够捕捉到金融市场中各种复杂的相依结构模式。

四、基于Copula函数的时间序列模型的估计方法

对Copula模型的参数估计广为采用的方法是极大似然估计，通过Copula密度函数和边际密度函数可以求出联合分布的密度函数，进一步可以得到样本的对数似然函数，根据多元函数的极值理论可以得到参数的极大似然估计量，但问题是同时估计所有参数会因为参数过多而使估计变得复杂。鉴于Copula函数可以将边际分布和联合分布分开来研究这一优良性质，因而在实践中一般采用两阶段极大似然估计法来估计模型中的参数，即首先估计出边际分布函数中的参数，然后将估计值当做已知数代入Copula函数中，从而得到Copula函数中的极大似然估计值［4］。当然两阶段极大似然估计在有效性方面要弱于一般的极大似然估计，然而Patton等通过仿真模拟发现两者在有效性方面差别并没有太大差别［5，8］。为了获得完全有效的参数估计，可以采用极大似然推断的多阶段迭代估计方法［9］。

从Skar定理可以看出Copula模型的良好性质，多元联合分布函数可以通过一个Copula函数来实现，联合分布函数中的参数估计可以对边际分布和Copula函数的参数分别进行估计。当边际分布的形式难以给定时，可以构建基于Copula函数的半参数模型。在这种情况下Copula参数的估计仍然采用极大似然法，一般称为“典型极大似然法”。Genest等研究了半参数模型中Copula参数的渐近分布以及模型的选择等问题，Chen等研究的是时间序列数据的半参数Copula模型的参数估计问题［10－11］。半参数模型估计相对于完全参数模型的困难之处在于似然函数依赖于待估计的非参数边际分布模型。Chen等给出了基于Copula函数的多元动态模型参数估计量服从渐近正态分布的若干条件，并且提供了一种估计多元Copula参数估计量的渐近协方差矩阵方法。但是，半参数Copula模型的估计需要建立在以下两个假设的基础之上：首先，多元Copula模型中的参数是不随时间变化的；其次，标准化残差所服从的边际分布是利用非参数估计方法得到的。

完全非参数Copula模型的估计相对于参数的主要优点在于不需要事先对描述变量间相依结构的Copula函数以及边际分布的任何参数做出假设和估计就可以直接估计得到任何一点处的Copula函数的值，进而可以对变量间相依结构作出描述，还可以得到一系列基于Copula函数的相依测度值，如Kendall秩相依系数和上下尾部相依系数等，因此非参数估计方法在应用中具有很大的优势。核估计是非参数估计领域应用比较广泛的一种方法［12］。核函数k （x）是一类在实数域内有界的对称函数，满k （x ）dx＝1，n元核函数的更一般表达式为：

核估计对于核函数和窗宽的选择比较严格，在实际应用中常常选用光滑的正态核函数，核函数一旦确定，窗宽的选择合适与否将对边际分布函数对样本数据的拟合优度产生重要影响。除此之外，当数据来源于某一确定分布时，利用非参数估计所得到的估计量的有效性难以保证。

以上所涉及的Copula模型和估计方法在实际应用中大都受到维数的限制，一般只讨论二维的情形，而对于三维以上的一般Copula模型在近两年才有所研究，所用的技术方法与二维情形有很大的区别，一种称之为“Vine Copulas”的多元Copula模型在金融领域表现出极大的优越性。Min等利用pair－Copula构造出一种灵活的Vine Copulas相依结构模型，并且利用贝叶斯估计方法进行分析，通过MCMC模拟得出pair－Copula构造的模型要优于任何其它现有多变量Copula模型［13－15］。

五、Copula模型拟合优度检验

根据数据的统计特征可以确定一种Copula函数来描述变量间的相关结构，但这往往具有一定的主观性，因而还要采用适当的拟合优度检验方法来检验所选的Copula函数是否合适。对于完全参数的Copula模型，由于这些模型仅仅涉及到非线性的时间序列模型，因而拟合优度检验的方法也比较固定，但获取拟合优度检验统计量临界值的困难之处在于统计量不仅依赖于Copula模型的参数估计，还依赖于边际分布函数中的参数估计。在这种情况下，Genest等指出一种行之有效的办法是通过模型模拟产生数据，先估计出边际分布中的参数，根据模拟数据计算出Copula参数的估计，然后计算拟合优度检验统计量，再经过多次重复试验得出统计量在模型正确设定的原假设下所服从的分布，根据分布得到相应的p值［16］。对于半参数模型，Chen等描述了一种基于模拟方法获取基于Copula函数的半参数马尔科夫模型拟合优度检验的临界值［11］。Rémillard考虑了基于Copula函数的半参数多变量时间序列模型的拟合优度检验［17］，同时他还证明了类似于Chen等研究中Copula参数的渐近分布的一个非常有用的结论：Copula模型的拟合优度检验的渐近分布不受边际分布中参数的影响，同时该文也提出了一种类似于上述完全参数模型但又更为简单的模拟方法［18］。

拟合优度检验的两种常用方法是Kolmogorov-Smirnov（K－S）检验和Cramér-von Mises（CvM）检验，这两类检验是比较常用的非参数检验方法，是建立在比较拟合模型和经验模型差异的基础之上的［17］。关于拟合优度检验的另一种方法是考虑Rosenblatt变换，它是基于多变量序列概率积分变换的一种检验方法。该方法首先是对变量进行概率积分变换，得到服从（0，1）上均匀分布的随机变量u，然后对变换后的数据应用K－S和CvM检验。基于经验模型而进行的拟合优度检验是建立在Copula相依参数为常数的假设基础之上，因而不适用于时变Copula模型。然而基于Rosenblatt变换的拟合优度检验倒更为灵活，不仅可以对时变模型进行检验，还可以用于马尔科夫Copula模型。Genest等基于前期有关Copula拟合优度检验的文献给出了比较详尽的评论，并通过数值模拟的手段对这些检验进行了优劣对比并总结得出CvM检验的效果最好［19］。Berg通过考虑其它拟合优度检验方法也进一步说明了这一点［20］。然而Genest等所提到的拟合优度检验都是通过数值模拟程序计算相应统计量的p值，但具体操作过程比较复杂。Fermanian等通过构造一种新的统计量提出了一种称之为渐近总变差检验的拟合优度检验方法［21］。该检验是通过构造经验Copula模型以及借助非参数自助法来计算相应的p值，其优点是即使在经验Copula模型不收敛的情况下也可以一致地估计出该统计量的p值，检验的效果比K－S检验要更好，但潜在的假设相依参数是常数，对于时变参数也不适用。进一步可以通过比较该检验与CvM方法的势的大小来判断拟合优度，另外通过调整Copula模型参数对所有这些拟合优度检验方法的对比以及基于Rosenblatt变换拟合优度检验的灵敏度研究也是值得尝试的工作。

六、Copula模型在金融领域的主要应用

近十几年来Copula理论在实证经济领域得到了极为广泛的应用，尤其在金融市场中具有独特的应用价值和广阔的应用前景。金融全球化加剧了世界金融市场之间的相互依存度，日益开放的全球金融市场使得资本能够在全球的金融市场间集中、迅速和自由地流动。无疑金融资本的自由流动提高了金融市场的效率，同时也极大地改变了金融市场的运转和操作模式，但资本在流动过程中也给全球金融市场带来了不稳定的因素，金融市场波动频繁，全球市场间传导机制的作用进一步加大，从而金融风险也呈现更高的复杂性。金融的剧烈频繁波动和金融危机的频发使得风险管理成为世界各国备受关注的课题，对金融时间序列分析也提出了更高的要求。传统的金融时间序列分析方法已经不能满足金融市场分析的需要，而Copula理论在金融市场分析中的应用将金融时间序列分析推到了一个新的阶段，为风险分析提供了新的工具。在此，本文简要举例说明基于Copula方法的金融时间序列模型的有关应用。

最早将Copula引入金融研究的是市场风险管理。基于风险价值（VaR）和其它度量最大损失的概率方法的风险管理需要不同的风险来源的相依结构模型。McNeil等详细阐述了Copula函数在市场风险管理中 的 应用［22］48－55，Cherubini等 采用 Copula方法研究了投资组合的风险［1］［23］153－178；韦艳华等比较全面地介绍了Copula函数在中国金融市场中的应用［24］74－121。

Copula在衍生品定价方面的应用早期主要有信用违约互换和抵押债务担保等。Li首先将Copula应用在信用风险的分析上，Hofert等利用阿基米德Copula讨论了CDO定价机制，还有一些文献讨论Copula函数在其它衍生品市场方面的应用［25－28］。

在投资组合决策方面，主要是需要预测各种资产组合的联合分布以便寻求投资者达到最大期望效用的投资权重，因而利用Copula来构造这种联合分布是最为方便的。Garcia等分析了涉及两国国家的股票和债券的投资组合问题，吴振翔等使用Copula－GARCH模型研究了股票市场的投资组合风险［6，29］。

基于Copula理论的应用早期几乎都局限于二维的情形，直到最近几年部分学者才集中于处理高维Copula的应用，但一般也是五维以下，对于更高维的情形还少有涉及，当然对于二维Copula的研究仍然比较盛行。对高维Copula函数的构造是受到Bedford等研究的启发，采用基于pair－Copula构造的藤结构Copula模型（Vine Copula），目前还仅限于C－Vine和D－Vine两种结构，对于其它藤结构的Copula模型还有待进一步的探求和研究［14－15］。Bedford等在简单构造模块pair－Copula的基础上引入了一种构造复杂多元相关结构模型的新方法，它将多元联合密度函数分解成一系列pair－Copula模块和边缘密度函数的乘积，为Copula方法推广到高维情况提供了理论基础。当变量间不存在条件独立性时，Vine－Copula模型的构造不要求条件独立假设，因而这种新的方法在描述高维相依结构时就更为灵活。近年来，Vine－Copula被用于金融资产收益率和套期保值等一些金融数据的建模［13，30－32］。

七、研究展望

鉴于大多数应用限于二维情形，笔者结合高维Copula建模最新进展，强调了一种新的多维Copula模型构造方法，即Vine－Copula模型，该方法在描述高维相依结构时具有很大的灵活性，而高维建模方法尚在探索阶段，在算法的改进上还有很大的空间，笔者相信基于时变Copula函数的高维建模和应用将是未来研究的热点。

Copula函数可以用一种简单的方式来描述变量间的复杂相依关系，因而在理论和应用上都受到广泛的重视，在分析变量间的关系时，允许事先分别对边际分布进行建模，然后再利用适当的Copula函数来研究变量间的相依关系。对高维Copula函数的构造研究和应用是受到Bedford等工作的启发，但由于统计推断技术上的困难，高维Copula函数建模以及相应的推断方法尚处于初步发展阶段，理论研究具有很大的发展前景。高维数据建模可以采用藤构造方法，Bedford等引入了一种pair－Copula构造（PCC）方法对复杂多元相关结构模型进行分析，它将多元联合密度函数分解成一系列pair－Copula模块和边缘密度函数的乘积，pair－Copula模块构造不要求条件独立的假设，因此这种新的方法在描述高维相关构建时具有很强的灵活性，为Copula方法推广到高维情形提供了方法论基础。理论上，可以对不同维度的数据结构采用Copula建模，但是模型估计和统计推断方法很受限制，如何采用一种有效的估计方法对各种高维Copula模型进行估计，相应的文献很少。对于二维或三维的数据结构来说，常常采用两步极大似然估计法、半参数估计或者矩估计方法，采用贝叶斯估计的文献相对较少。然而，贝叶斯估计法在很多多变量模型中被广为采用，对于高维Copula模型的估计，利用贝叶斯估计所存在的技术上或理论上的困难还值得我们进一步思考和研究。

［1］ Embrechts P，Heing A，Juri A．Using Copulae to Bound the Value-at-Risk for Functions of Dependent Risks［J］．Finance and Stochastics，2003，7（2）．

［2］ Nelsen R B．An Introduction to Copulas［M］．New York：Springer Press，2006．

［3］ Engle R．Dynamic Conditional Correlation：A Simple Class of Multivariate Generalized Autoregressive Conditional Heteroskedasticity Models［J］．Journal of Business ＆ Economic Statistics，2002，20（3）．

［4］ Patton A J．Estimation of Multivariate Models for Time Series of Possibly Different Lengths［J］．Journal of Applied Econometrics，2006，21（2）．

［5］ Patton A J．Modelling Asymmetric Exchange Rate Dependence［J］．International Economic Review，2006，47（2）．

［6］ Garcia R，Tsafack G．Dependence Sructure and Extreme Comovements in International Equity and Bond Markets［J］．Journal of Banking ＆ Finance，2011，35（8）．

［7］ 蔡晓薇．MCMC方法下最优Copula的估计及选取［J］．统计与信息论坛，2011，26（10）．

［8］ Nikoloulopoulos A K，Joe H，Li H．Vine Copulas with Asymmetric Tail Dependence and Applications to Financial Return Data［J］．Computational Statistics ＆ Data Analysis，2012，56（11）．

［9］ Song P，Fan Y，Kalbfleisch J D．Maximization by Parts in Likelihood Inference［J］．Journal of American Statistical Association，2005，100（4）．

［10］Genest C，Ghoudi K，Rivest L P．A Semiparametric Estimation Procedure of Dependence Parameters in Multivariate Families of Distributions［J］．Biometrika，1995，82（3）．

［11］Chen X，Fan Y．Estimation of Copula-based Semiparametric Time Series Models［J］．Journal of Econometrics，2006，130（2）．

［12］Fermanian J D，Scaillet O．Nonparametric Estimation of Copulas for Time Series［J］．Journal of Risk，2003（5）．

［13］Min A，Czado C．Bayesian Inference for Multivariate Copulas Using Pair-copula Constructions［J］．Journal of Financial Econometrics，2010，8（4）．

［14］Bedford T，Cooke R M．Probability Density Decomposition for Conditionally Dependent Random Variables Modeled by Vines［J］．Annual of Mathematics and Artificial Intelligence，2001，32（1）．

［15］Bedford T，Cooke R M．Vines－A New Graphical Model for Dependent Random Variables［J］．Annual of Statistics，2002，30（4）．

［16］Genest C，Rémillard B．Validity of the Parametric Bootstrap for Goodness-of-fit Testing in Semiparametric Models［J］．Annales de Linsitut Henri Poincare Probability and Statistics，2008，44（6）．

［17］Rémillard B B．Goodness-of-fit Tests for Copulas of Multivariate Time Series［R］．Working Paper，HEC Montréal，Canada，2010．

［18］Chen X，Fan Y．Estimation and Model Selection of Semiparametric Copula-based Multivariate Dynamic Models under Copula Misspecification［J］．Journal of Econometrics，2006，135（1）．

［19］Genest C，Rémillard B，Beaudoin D．Goodness-of-fit Tests for Copulas：A Review and a Power Study［J］．Insurance，Mathematics ＆ Economics，2009，44（2）．

［20］Berg D．Copula Goodness-of-fit Testing：An Overview and Power Comparison［J］．European Journal of Finance，2009，8（15）．

［21］Fermanian J D，Wegkampb M H．Time-dependent Copulas［J］．Journal of Multivariate Analysis，2012，110（3）．

［22］McNeil A J，Frey R，Embrechts P．Quantitative Risk Management：Concepts，Techniques and Tools［M］．Princeton：Princeton University Press，2005．

［23］Cherubini U，Luciano E，Vecchiato W．Copula Methods in Finance［M］．England：Wiley Press，2004．

［24］韦艳华，张世英．Copula理论及其在金融分析上的应用［M］．北京：清华大学出版社，2008．

［25］Li D X．On Default Correlation：A Copula Function Approach［J］．Journal of Fixed Income，2000，9（4）．

［26］Hofert M，Scherer M．CDO Pricing with Nested Archimedean Copulas［J］．Quantitative Finance，2011，11（5）．

［27］Hu L．Dependence Patterns across Financial Markets：A Mixed Copula Approach［J］．Applied Financial Economics，2006，16（10）．

［28］Taylor S J，Wang Y．Option Prices and Risk-neutral Densities for Currency Cross-rates［J］．Journal of Futures Markets，2010，30（4）．

［29］吴振翔，叶五一，缪柏其．基于Copula的外汇投资组合风险分析［J］．中国管理科学，2004，27（4）．

［30］杜子平，闫鹏，张勇．基于“藤”结构的高维动态copula的构建［J］．数学的实践与认识，2009，39（10）．

［31］黄恩喜，程希俊．基于pair-copula-GARCH模型的多资产组合VaR分析［J］．中国科学院研究生院学报，2010，27（4）．

［32］Aas K，Czado C，Frigessi A，et al．Pair-copula Constructions of Multiple Dependence［J］．Insurance，Mathematics ＆Economics，2009，44（2）．

A Review on Copula-based Financial Time Series Models

ZHANG Chao-feng1，2，ZHANG Li-min2
（1．School of International Trade and Economics，University of International Business and Economics，Beijing 100029，China；2．School of Mathematics and Finance-economics，Sichuan University of Arts and Science，Dazhou 635000，China）

This survey reviews the large and growing literature on Copula-based models for financial time series．Copula-based models have a very flexible property that they allow the researcher to specify the models for the marginal distributions separately from the dependence structure．This makes specifying and estimating the models more convenient and easier．The construction of the time series models，the choice of Copula function and inference methods as well as good-of-fit tests are reviewed．The last part is some applications of these Copulas for financial time series．

Copula function；dependence structure；financial time series

F830．9∶O212

A

1007－3116（2014）04－0003－07

2013－11－08；修复日期：2014－01－12

四川省自然科学基金项目《转型期股市投资组合风险度量建模与实证研究》（13ZB0102）

张超锋，男，河南嵩县人，博士生，讲师，研究方向：计量经济学及其应用；

张莉敏，女，河南柘城人，理学硕士，讲师，研究方向：应用数学。

（责任编辑：崔国平）