基于灰度阶的特征描述子研究

张树静,闫宇

（1.河南科技学院,河南新乡 453003；2.上海交通大学,上海 200240）

特征描述的方法已经广泛应用于计算机视觉的许多领域,比如目标识别与跟踪、纹理识别、宽基线匹配、图像检索和全景图像拼接等.其基本思想是在检测感兴趣点或感兴趣区域的基础上计算不变特征描述子.通过计算获得特征描述子,可以使得不同图像之间的特征匹配在一些相似性度量下得到自动确定.

特征描述的方法主要分为3类：基于灰度值、基于灰度阶以及基于灰度值与灰度阶结合的方法.基于灰度值的特征描述方法中最著名的是SIFT（Scale Invariant Feature Transform）[1],SIFT主要是通过创建梯度方位和位置直方图的方式进行特征描述.此方法对一定的尺度变化、旋转和平移具有不变性.然而,当图像出现大的视角变化时,算法性能就会降低,并且计算过程非常耗时.Daisy[2]同样依赖于梯度直方图,与SIFT不同的是,它通过使用高斯权重和圆形对称核与方位地图进行卷积,从而大大提升了密集计算的速度.这种基于灰度梯度的描述子通常能获得较好的性能.然而,尽管上述描述子对许多变化或变形具有鲁棒性,但是它们不能处理复杂的光照变化,包括伽马修正和小的镜面反射,以及在曝光时间内的变化等.为了解决上述问题,一些学者提出使用灰度阶来描述特征.Tang等[3]通过创建2D直方图的方式编码序数分布和空间分布.Gupta等[4]提出了一种鲁棒的方法HRI-CSLTP（Histogram Relative Intensity-Central Symmetric Local Ternary Patterns）,其包含两部分：相对灰度直方图和CS-LTP编码直方图.随后,Wang等[5]提出一种新的基于灰度阶的特征描述方法LIOP（Locality Intensity Order Pattern）,其基本原则是当灰度变化呈现单调性时,像素灰度的相对阶保持不变.Fan等[6]提出了两种特征描述子：MROGH（Multi-Support Region Order-based Gradient Histogram） 和 MRRID（Multi-Support Region Rotation and Intensity Monotonic Invariant Descriptor）,并指出两者具有旋转不变性并且不依赖于指定的参考取向,同时具有很高的区分性.

为了进一步探究上述各种描述子的性能,以便更好地服务于实际工程应用,本文基于灰度阶的特征描述方法,首先分析了各种方法的组成及其在不同场景下的应用；其次利用不同场景下的图像进行测试,评估各种方法的性能；最后通过实验比较分析各种方法的应用场景,为其后续的实际工程应用提供指导作用.

1 实验原理及方法

利用特征描述子匹配图像中的点主要有3个步骤：①检测图像中的感兴趣点或感兴趣区域.被检测的点应该在不同成像条件下的图像间被检测和匹配,这些点称作感兴趣点或特征点.特征点检测通常跟随额外的步骤,检测感兴趣点周围的仿射不变区域,以便处理大的视角变化.②在上述检测到的感兴趣区域（仿射归一化）中建立特征描述子,以便将其区分开来.③计算两个候选点描述子之间的距离以决定是否是一个正确的匹配.

1.1 基于灰度阶的特征描述方法

本文以基于灰度阶的特征描述方法中具有代表性的4种描述子（HRI-CSLTP,LIOP,MROGH和MRRID）为例,分析这几种描述子的建立过程.

1.1.1 H RI-CSLTP方法 HRI-CSLTP是Gupta等[4]提出一种鲁棒的基于灰度阶的特征描述方法,其包含两部分：相对灰度直方图和CS-LTP编码直方图.与大多数描述子一样,首先需要检测图像中的感兴趣点或感兴趣区域.被检测的点应该在不同成像条件下的图像间可以被检测和匹配.部分学者已经提出许多方法用来检测感兴趣点或与某一类变换（如仿射变换）具有协变式的感兴趣区域.如Harris角点检测子[7]和DOG（Difference of Gaussian）用来检测感兴趣点,Harris-affine,Hessian-affine,MSER（Maximally Stable ExtremalRegion）和EBR（Edge-Based Region）用来检测仿射协变区域.HRI-CSLTP采用广泛使用的仿射协变区域检测子Harris-affine和Hessian-affine来定位特征位置和估计其邻域的仿射形状.由于检测到的区域尺寸和形状各异,文中将其归一化到固定直径的圆形区域.为了消除在归一化步骤中由于差值引入的噪声,使用高斯平滑滤波器消除噪声影响,最后得到局部块.

为了提升区分性,需要将上述得到的局部块分割为一些子区域,分别计算每个子区域的直方图,将其连接起来建立描述子.HRI-CSLTP将空间位置量化为4*4的网格.对每个局部块,必须估计一个局部连续的取向,然后相对于这个取向建立描述子以获得旋转不变性.

在对区域进行划分之后,建立描述子.HRI-CSLTP采用两种技术：相对灰度直方图HRI和中心对称局部三值模式（CS-LTP）.前者首先根据局部块（patch）的灰度起点和终点将灰度范围分为k个相同的间隔,获得每个间隔大小.然后将局部块（patch）分为s*s个空间bins,对每一个空间bin,根据像素灰度范围建立直方图,因此获得s*s*k个bins.虽然它作用于块（patch）的整体分布,但它没有捕捉到局部梯度信息,而这些信息与全局阶信息具有互补作用.因此,后者主要作用于局部梯度信息,它在CS-LBP的基础上,采用第三个值来表示几乎具有相同灰度值的像素.然而,如果采用类似于CS-LBP的比较方法,将获得81bins的直方图.为了减小直方图的尺寸,只考虑两次比较.由于特征归一化和通用的图像特征,仅采用对角比较就足以生成CS-LTP编码,由此对于每个空间bin可以获得9bins的直方图.对于值为1的编码,也即两个匹配点的灰度值相差很小,更倾向于漂移,因此赋予更小的权重.因此,每个空间bin的数量减小到8,生成s*s*8维的CS-LTP描述子.将前者与后者得到的直方图连接起来形成最后的描述子.然而,由于上述描述子只比较中心对称邻域采样点的灰度,不能有效捕捉邻域采样点灰度之间的关系.此外,它需要分配一个参考取向以获得旋转不变性,这使得它对方位估计误差比较敏感.

获得描述子向量之后的问题就是如何计算两个候选点之间的距离,从而判定这两个点是否是匹配点.目前最著名的决策策略是最近邻（Nearest Neighbour,NN）和最近邻距离比（Nearest Neighbour Distance Ratio,NNDR）[8].此外,EMD（Earth Movers Distance）对于许多描述子表现出更优的性能.因此,HRI-CSLTP[4]采用EMD来匹配两个描述子向量之间的相似性.对于直方图而言,EMD定义为将一个直方图转换到另一个直方图的最小代价,在直方图的bins之间有一个“基准距离”.基于数学的分析角度,这是一个最小代价流问题,可以利用线性规划来解决.

1.1.2 L I OP方法 LIOP（Locality Intensity Order Pattern）,即局部灰度阶模式,是Wang等[5]提出的一种新的基于灰度阶的特征描述方法,其基本原则是当灰度变化呈现单调性时,像素灰度的相对阶保持不变.

与HRI-CSLTP一样,LIOP采用广泛使用的仿射协变区域检测子Harris-affine和Hessian-affine来定位特征位置和估计其邻域的仿射形状.由于检测到的区域尺寸和形状各异,同样将其归一化到固定直径的圆形区域.为了消除在归一化步骤中由于差值引入的噪声,使用高斯平滑滤波器消除噪声影响,最后得到局部块.

为了提升描述子区分性,LIOP采用了基于灰度阶的区域划分方法.首先,局部块中的所有像素按其灰度大小进行非降序排列.其次,根据排序将局部块等量量化成B个序数bins.因此,它不仅对单调灰度变化和图像旋转不变,同时比上述环形区域划分方法包含更多的空间信息.

对区域进行划分之后,建立描述子.为了克服HRI-CSLTP对方位估计误差比较敏感的问题,LIOP使用所有采样邻域点的灰度阶来挖掘局部信息.此外,它采用旋转不变采样方法以避免局部连续取向带来的误差,因此获得了更高的区分性.然而,对于一个特定尺寸的支持域（support region）,当两个非对应点具有相似的表观模型时,LIOP可能将其认为是一对对应点,因此区分性消失.

获得描述子向量之后的问题就是如何计算两个候选点之间的距离,从而判定这两个点是否是匹配点.LIOP采用著名的NNDR（Nearest Neighbour Distance Ratio）匹配策略来计算两个特征点描述子向量之间的点积,如果第一个和第二个最近邻点的距离比值小于某一阈值,则认为是一个匹配.

1.1.3 MROGH和M RRID方法 由于MROGH和MRRID均是由Fan等[6]提出的,有较多相似之处,本文将其进行统一分析.MROGH（Multi-Support Region Order-based Gradient Histogram）[9]和 MRRID（Multi-Support Region Rotation and Intensity Monotonic Invariant Descriptor）[10]采用两种不同的局部特征,前者联合灰度阶和梯度信息,后者完全基于灰度阶,因此后者不仅能适应线性光照变化,对于大的光照变化也具有一定的鲁棒性.除此之外,它们具有旋转不变性而不依赖于指定的参考取向,同时具有很高的区分性.

与前面两种描述子一样,MROGH和MRRID采用广泛使用的仿射协变区域检测子Harris-affine和Hessian-affine来定位特征位置和估计其邻域的仿射形状.随后再将其归一化到固定直径的圆形区域.图1展示了归一化区域的一个案例.支持域被归一化到圆形区域,归一化的点的灰度通过双线性差值获得.为了消除在归一化步骤中由于差值引入的噪声,使用高斯平滑滤波器消除噪声影响,最后得到局部块.

图1 将被检测区域仿射归一化到圆形区域Fig.1 Affine detection area will be normalized to a circular area

在获得局部块之后,将上述得到的局部块分割为一些子区域,分别计算每个子区域的直方图,将其连接起来建立描述子.与LIOP一样,MROGH和MRRID[6]也是基于灰度阶来划分子区域.基于此类情况,每一组中的采样点不需要空间相邻,并且这种自适应划分方法不需要分配一个参考取向,从而大大提升了描述子的区分性.

在对区域进行划分的基础之上,MROGH和MRRID采用多个不同尺寸的支持域来建立描述子.与LIOP类似,它们同样采用基于灰度阶和旋转不变采样的方法来建立描述子,在保持鲁棒性的同时进一步提升了描述子的区分性.

与LIOP一样,MROGH和MRRID采用著名的NNDR（NearestNeighbour Distance Ratio）匹配策略来计算两个特征点描述子向量之间的点积,如果第一个和第二个最近邻点的距离比值小于某一阈值,则认为是一个匹配.

1.2 数据集和评估准则

为了评估上述各种特征描述子的性能,本文选择来自于牛津大学网站的标准Oxford数据集.它包含结构和纹理场景的几何和光学变换图像.6种不同的变换分别为：视角变化、尺度变化、图像旋转、图像模糊、光照变化和JPEG压缩.实验在Inte（lR）Core（TM）CPU 3.10Ghzde的PC机上进行,仿真环境为MATLABR2010a.此外,选择Mikolajczyk和Schmid[8]提出的评估准则来评价描述子匹配的性能.它基于两幅图像之间正确匹配和错误匹配的数量.匹配策略以NNDR为例,如果第一个和第二个最近邻点的距离比值小于某一阈值,则认为是一个匹配.正确匹配和基准对应点的数量由重叠误差来确定.如果重叠误差小于0.5,则认为是一对正确匹配.结果可以用精度召回曲线来表示

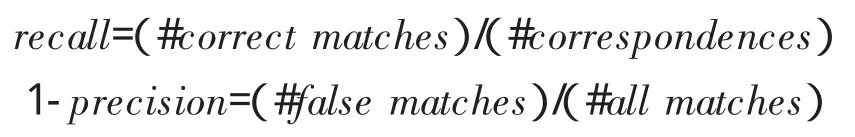
其中#correspondences是匹配的基准数量,#correct matches表示正确匹配的点对数量,#false matches表示错误匹配的点对数量,#allmatches表示所有匹配的点对数量.精度越高,recall越大.

1.3 参数选择

对于LIOP,同样按照Wang等[5]实验使用的参数,一共有6个：①区域检测前的高斯平滑核σp；②区域归一化后的高斯平滑核σn；③序数bins的数量B；④邻域采样点数N；⑤采样半径R；⑥权重函数的阈值Tlp.实验发现,当σp=1.0,σn=1.2,N=4,B=6,R=6,Tlp=5时能获得更好的性能.就针对HRI-CSLTP,空间bins的数量为4*4,对于相对灰度直方图,每个空间bin按灰度值范围分为16个bins；对于中心对称局部三值模式,邻域距离D=2,阈值T=3.对于MROGH和MRRID,需对部分参数进行设置：空间划分数量k,支持域的数量N,方位bins d,二值编码数量m.考虑到描述子的性能和复杂度的折中,对于MROGH,实验设置参数d=8,k=6,N=4；对于MRRID,m=4,k=4,N=4.因此,MROGH描述子有192维,MRRID描述子由256维.

2 结果与分析

为了比较上述基于灰度阶的特征描述方法的性能,在标准Oxford数据集上进行实验和分析,其中每个数据集包含6幅图像,采用广泛使用的仿射协变区域检测子：Harris-affine（haraff）.Hesaff检测blob-like结构,输出尺寸不一的椭圆形区域,然后将其归一化到固定直径（41个像素）的圆形区域.

为了评估MROGH对方位估计误差的不敏感性（由于其不需要分配方位取向）,将其与SIFT描述子（需要分配方位取向）作比较,将得到的纽约城市的两幅大幅度旋转（旋转角度超过200）图像进行关键点匹配,获得的匹配结果如图2所示.图中深色线表示正确匹配的点对,浅色线表示错误匹配的点对.在图像发生较大角度的旋转时,采用MROGH描述子可以获得大量正确匹配点对,而SIFT描述子会出现很多错误匹配.从而验证了MROGH对方位估计误差的不敏感性.

图2 SIFT和MROGH对应点匹配结果Fig.2 SIFT and MROGH corresponding points matching results

为了定量评估描述子在视角、光照、旋转和尺度变化下的匹配性能,将HRI-CSLTP、LIOP、MROGH和MRRID描述子与广泛使用的SIFT和DAISY描述子进行比较.由于空间限制,对于Oxford数据集,只展示各种描述子在每种情况下的图像对1-2（第一幅vs第二幅）和1-4（第一幅vs第四幅）上分别使用Harris-affine（haraff）和Hessian-affine（hesaff）区域上的评估结果,如图3所示.图3中每一行图像分别为不同描述子使用Harris-affine区域检测子在图像对1-2和1-4上的评估结果.

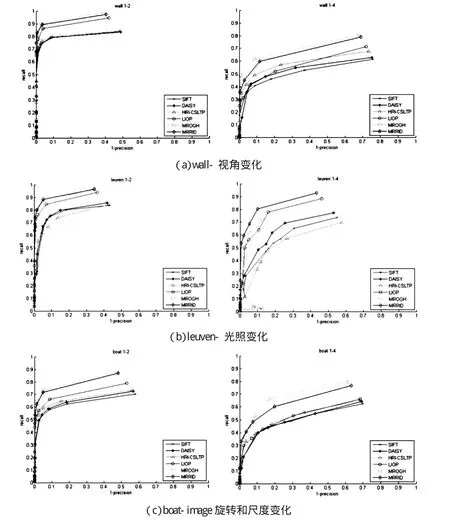
图3 实验结果Fig.3 Experimental results

对于同一个数据集,当图像发生较大变化（图像4相对于图像1）时,描述子整体性能呈现下降趋势.对于光照变化（图3（b））,相对于其它描述子,MRRID表现出最好的性能.当光照变化较小时（图3（b）左边）,MRRID性能最好,MROGH次之,LIOP稍逊,均优于SIFT、DAISY和HRI-CSLTP；当光照变化剧烈时（图3（b）右边）,MRRID性能依然保持最好,MROGH与LIOP相当,HRI-CSLTP性能最差.这是由于MROGH、MRRID和LIOP均使用了灰度阶,这比单纯使用灰度（SIFT、DAISY和HRI-CSLTP）能更好地处理复杂的光照变化.

除了光照变化之外,对于图像发生视角、旋转、尺度变化的情况,以上基于灰度阶的描述子中,MROGH均表现出最好的性能,MRRID次之,LIOP最差.

综上所述,基于灰度阶的特征描述子在处理许多图像变换时性能均优于基于灰度值的描述子,尤其在处理复杂的光照变化时区分性更强,性能进一步提升.

3 小结

本文首先分析了近年来一些主流的基于灰度阶的特征描述方法,如HRI-CSLTP、LIOP、MROGH和MRRID.其次,评估了描述子在视角、光照、旋转和尺度变化下的匹配性能,将HRI-CSLTP、LIOP、MROGH和MRRID描述子与广泛使用的SIFT和DAISY描述子进行了比较分析.最后,通过实验比较分析了不同描述子在不同场景下的性能.实验结果表明,基于灰度阶的特征描述子在处理许多图像变换时性能均优于基于灰度值的描述子,尤其在处理复杂的光照变化时区分性更强,性能进一步提升.上述分析和评估不仅有利于在特定应用情况下选择合适的算法,同时为后续设计新的特征描述方法以及应用到工程实践中提供一定的借鉴.

[1] Lowe D G.Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision,2004,60：91-110.

[2] Tola E,Lepeit V,Fua P.Daisy：An efficient dense descriptor applied to wide-baseline stereo[J].Pattern Analysis and Machine Intelligence,2010,32：815-803.

[3] Tang F,Lim S H,Chang N,et al.A novel feature descriptor invariant to complex brightness changes[C]//IEEE Conf.Computer Vision and Pattern Recognition.[S.l.]：IEEE,2009,2631-2638.

[4] Gupta R,Patil H,Mittal A.Robust order-based methods for feature description[C]//IEEE Conf. Computer Vision and Pattern Recognition.[S.l.]：IEEE,2010,334-341.

[5] Wang Z H,Fan B,Wu F C.Locality intensity order pattern for feature description[C]//IEEE International Conference on Computer Vision.IEEE,2011,603-610.

[6] Fan B,Wu F,Hu Z.Rotationally invariant descriptors using intensity order pooling[J].Pattern Analysis and Machine Intelligence,IEEE Transactions on,2012,34（10）：2031-2045.

[7] Harris C,Stephens M.A combined corner and edge detection[C]//Alvey Vision Conference,1988：147-152.

[8] Mikolajczyk K,Schmid C.A performance evaluation of local descriptors[J].Pattern Analysis and Machine Intelligence,2005,27（10）：1615-1630.

[9] Wang H,Ullah M M,Klaser A,et al.Evaluation of local spatio-temporal features for action recognition[C]//Proc.British Machine Vision Conf,2009：1-11.

[10] Rao C,Yilmaz A,Shah M.View-invariant representation and recognition of actions[J].International Journal of Computer Vision,2002,50（2）：203-226.