PSA贴敷设备的精度分析和几何误差建模

张 锋，鲍 磊，孙瑞涛，王福闯，邵 敏

（机科发展科技股份有限公司，北京 100044）

0 引言

PSA（Pressure Sensitive Adhesive）即指压敏胶（在较小的压力作用下，即可与被粘物牢固粘合的一类胶粘剂），在柔板电路板制造行业中，PSA特指单面涂敷了压敏胶的塑料薄片，通常用于定位柔板或局部电气、机械保护[2]。

柔性印刷电路板(Flexible Printed Circuit，简称FPCB，柔板)的制造过程中，需要粘贴数量巨大的PSA胶片，而且为了满足下游工序，必须保证PSA胶片的贴敷位置极其精确。而为了适应柔板复杂的形状，PSA胶片大多面积小、形状复杂，加之其极为轻、薄的特点，要求实现这一工艺的自动化设备具有非常高的精度和稳定性。

现代制造业的主要特点是高效率和高精度，制造业自动化设备的精密程度逐步提高。而现代电子制造业对生产线设备的性能要求尤为严格，作为柔板制造生产线中的关键设备之一，对于PSA贴敷设备的研究越来越为人们所重视。

本文首先分析了PSA贴敷工艺对精度的具体要求，其次针对影响误差的关键因素——几何误差部分，运用多体运动学理论建立了PSA贴敷设备的几何误差数学模型，并通过对该模型的简化，分析了影响PSA贴敷精度的主要误差因素，为设备实施误差补偿和精度优化提供了理论基础。

1 精度要求

根据柔板生产线下游工序对PSA位置的要求，提出了自动PSA贴敷机需要达到贴敷PSA的位置精度为±0.1mm。根据现场质量检验的标准，分析该±0.1mm的具体意义，有助于在下一步对误差进行分析时更有针对性。

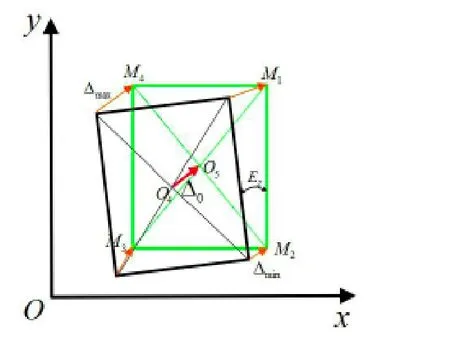
图1 PSA贴敷偏差示意图

如图1所示，虚线框为PSA胶片目标贴敷位置轮廓，假设实线线框为实际贴敷位置轮廓。而O5和O4两点是吸附与设备吸嘴上的PSA胶片的理论和实际旋转中心。那么贴敷偏差实际是中心偏差向量 和一个旋转角度偏差EZ叠加的效果之和。

根据质量检验的标准，±0.1mm的精度要求是指，在轮廓上指定的所有的mark点（标记点），图中是M1到M4，它们的贴敷实际位置与理论位置的距离偏差均不能超过0.1mm。那么总偏差是由一个平移偏差和旋转造成的偏差相叠加产生的，考虑最差情况——在距旋转中心最远点，旋转造成的偏差恰好与中心位置偏差向量O4O5（平移偏差）平行且同向，则产生最大位置偏差值：

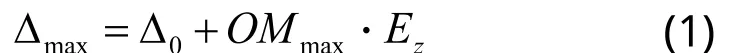
而根据±0.1mm的最大误差值，可以得到下式：

所以在误差分析和优化时需要重点关注的是ΔX、ΔY和EZ这三项误差。

2 设备几何误差建模

几何误差是设备整体误差的主要组成部分，因此系统地建立其误差模型具有重要的意义。

2.1 设备结构描述

本文所研究的PSA贴敷设备为龙门双驱的拱顶式结构，如图2所示。设备主要工作端为一个搭载了6组并行吸嘴的贴装头，贴装头可以在x-y平面内大范围移动，吸嘴可以沿z轴上下运动和绕z轴旋转完成贴敷PSA工作，而输送和翻转柔板的滑台只在x方向运动[2]。

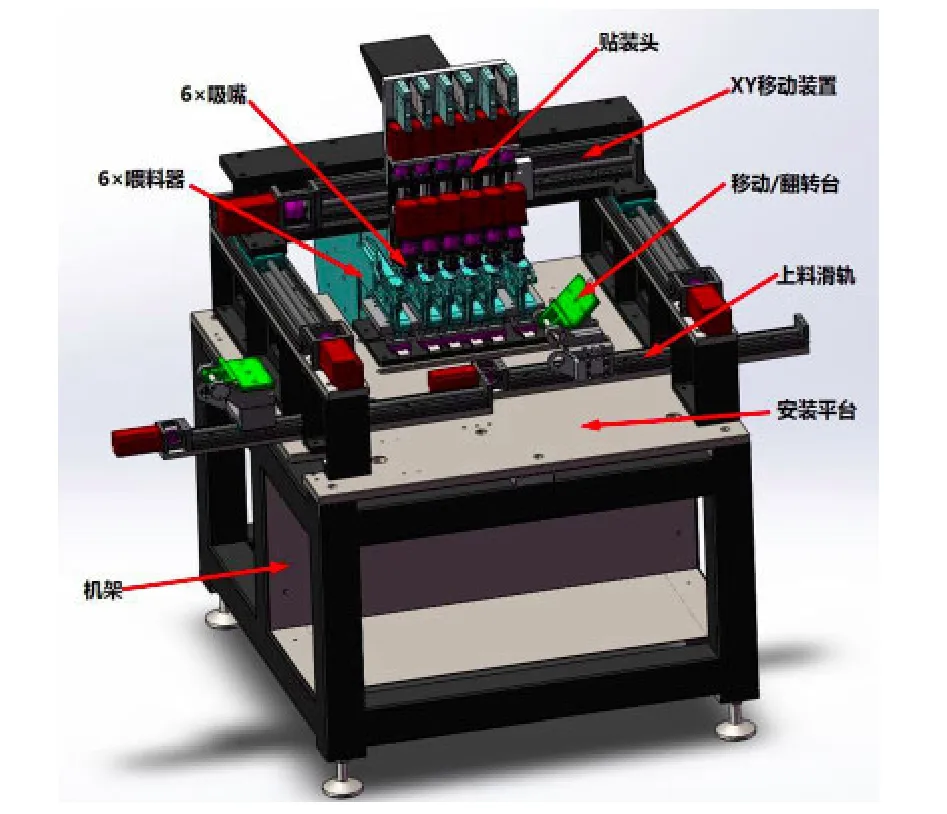
图2 设备主体结构图

2.2 坐标系设定

为了研究运动副在运动过程中误差分量的变化情况，需要建立起一系列的坐标。首先在PSA贴敷设备的固定部件（安装平台）上建立一个基坐标系，然后在每个独立运动的构件上建立一个坐标系，坐标系的方向选择尽量一致，以便于简化模型。

图3 PSA贴敷设备的坐标系建立

根据多体系统运动学理论，设置PSA贴敷设备的坐标系如图3所示，其中安装平面为固定惯性体B0：O0—X0Y0Z0；横梁为沿x方向运动的B1体：O1—X1Y1Z1；贴装头为B2体：O2—X2Y2Z2；吸嘴升降滑枕为B3体：O3—X3Y3Z3；吸嘴为B4体：O4—X4Y4Z4；上料或下料滑台为B5体：O5—X5Y5Z5。其拓扑结构如图4所示。

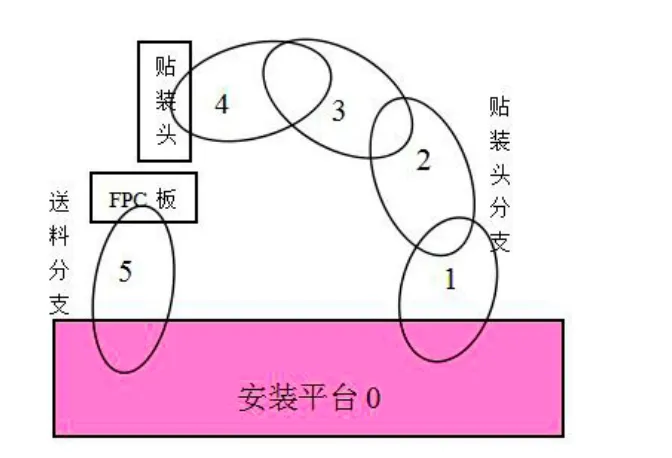
图4 PSA贴敷机拓扑结构图

2.3 几何误差分析

PSA贴敷设备的主要运作段，可以抽象成一个开环的多体系统，按照设备运动模式划分为两个基本分支，即柔板输送定位分支和贴装头定位分支，如图4所示，而其中以贴装头定位分支最为复杂。

PSA贴敷设备运动系统的串联分支实际是一系列的运动副的连接，最终实现的是柔板与贴装头的相对运动，而这个分支中所有运动副的精度都或多或少地影响最末端两个工件的相对定位精度。

每对相邻的运动构件之间由一个运动副相连，在理想情况下，运动副只有一个自由度，即移动副仅有一个平移方向的自由度，而转动副只有一个旋转的自由度。但在实际设备中，由于制造和装配上引入的误差，运动副并没有完全约束住其他5个方向上的自由度，实际上在6个空间方向上还均有误差元素的存在。

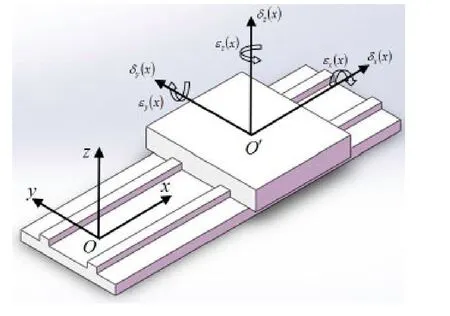
图5 移动副误差元素

如图5所示，为简化的移动副连接，其中滑台沿着固定在坐标系O上的滑轨沿x轴方向运动，而实际上，此时滑台除了具有x方向移动的自由度，还存在3个平移运动误差分量——名义运动方向的线性位移误差δx(x)和y、z方向的直线度误差δy(x)、δz(x)；除此还有3个转角运动误差分量——滚转误差εx(x)、俯仰误差εy(x)和偏转误差εz((x)。其中下标x，y，z分别表示误差运动的方向。转动副中引入的误差元素与此类似，在此不再赘述[1]。

本文通过对PSA贴敷设备各个主要运动部件的分析，得出了设备全部34项几何误差元素，如表1所示。

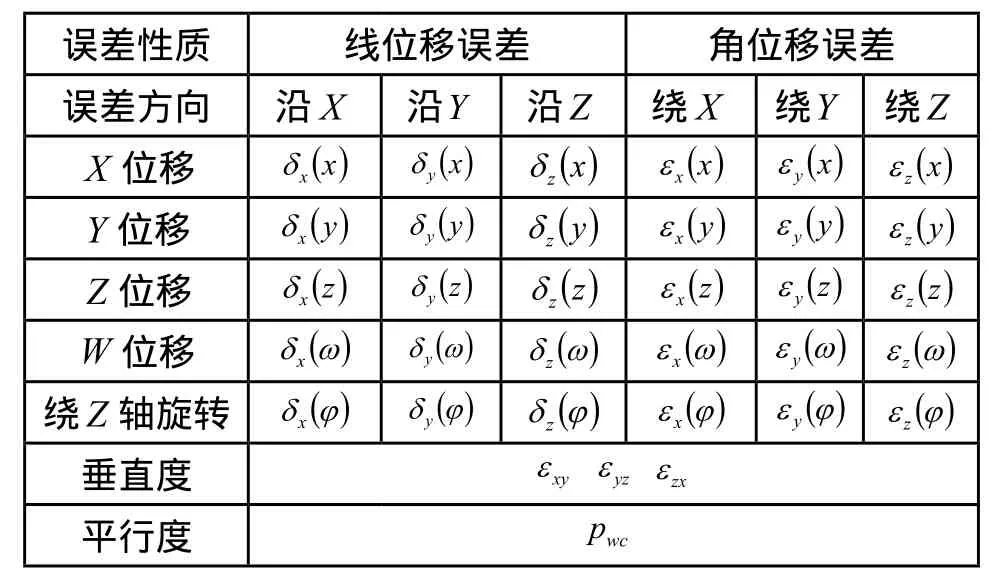
表1 PSA贴敷设备的34项几何误差元素

2.4 几何误差数学模型

从PSA贴敷设备的结构示意图和拓扑结构可以看出，对于柔板，安装平台运动链有1个移动运动副相连而成；对于吸嘴末端，安装平台运动链由4个运动副串联而成，其中3个移动副，1个转动副。

分别沿安装平台-FPC板和安装平台-贴装头两条传递链建立误差运动方程：

1）安装平台——柔板：

那么在实际贴敷过程中，贴装头与FPC板之间的几何误差为：

根据坐标系特征矩阵的规律，建立运动构件之间的误差运动特性变换矩阵。各矩阵如下所示：

吸嘴滑台坐标系至吸嘴端点坐标系的传递矩阵。

将以上各式代入（5）式可得：

此式为PSA贴敷设备的运动学约束方程，∑即为PSA贴敷设备的综合误差矩阵。式中，Δx、Δy、Δz即是吸嘴末端相对于柔板理论位置的X、Y、Z方向偏差，Ex、Ey为吸嘴末端相对于X、Y轴的旋转误差，这两个偏差对最终精度影响甚小，而EZ为吸嘴相对于Z轴的旋转偏差。

3 误差模型的综合分析

解式（6），并忽略高阶小项，可得：

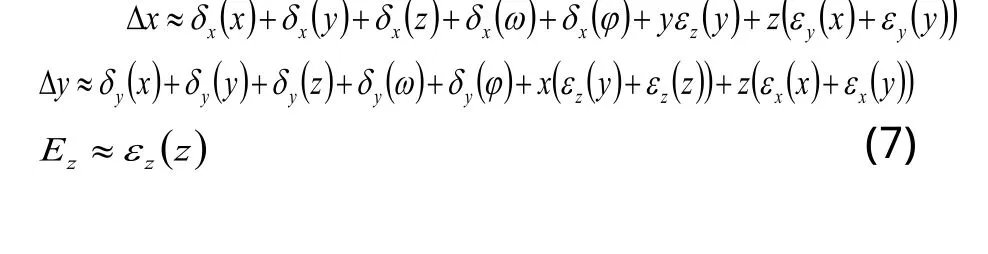
从误差补偿运动角度来看，由于方向误差Δz、Ex、Ey对最终精度没有意义，不再计算。

从以上数据可以看出，δx(x)、δy(x)、δz(x)等10项线性位移误差直接影响定位精度，而εx((x)、εy(x)、εz(x)等15项角位移误差中只有8项间接影响定位精度。

考虑到几何误差的构成，它的每一项几何误差元素为以下四项的贡献之和：

1）静力变形；

2）装配误差；

3）电机及模组精度；

4）传动中的几何误差。

在设备的精度优化中，应从这四个方面分别考虑降低18项间接影响定位精度的误差元素，最终降低主要误差项xΔ、yΔ、zE，以提高设备加工精度。

4 结论

本文分析了柔板生产流程中贴敷PSA工艺对精度的要求，指出了影响精度的主要误差项；根据多体运动学理论建立了该PSA贴敷设备的几何误差数学模型，分析了影响精度的主要误差元素，为PSA贴敷设备实施误差补偿和精度优化提供了理论基础。

[1] 任永强,杨建国,等.五轴数控机床综合误差建模分析[J].上海交通大学学报,2003,37(1):70-75.

[2] 孙瑞涛,鲍磊,等.全自动贴敷PSA设备的研制[J].电子工业专用设备,2013(03):52-55.

[3] 刘宝俊,梁睿君,等.龙门机床几何误差建模与补偿研究[J].组合机床与自动化加工技术,2012(06):16-19.

[4] 杨建国.数控机床误差综合补偿技术及应用[D].上海:上海交通大学机械工程学院,1998.

[5] 熊有伦.机器人学[M].北京:机械工业出版社,1993.