全电力船舶的电力推进系统建模与仿真

杨明国



全电力船舶的电力推进系统建模与仿真

杨明国

（海军驻七一二所军事代表室，武汉 430064）

本文介绍了全电力船舶的典型推进系统并给出了仿真结果。由于模型的复杂性，仿真计算的工程量非常巨大。因此设计了一个可供替代的简化仿真系统。从船舶网络的角度来看，简化系统的仿真结果和实际模型的结果十分接近。

船舶推进 谐波失真 负载换相逆变器（LCI） 双三相同步电动机

0 引言

综合电力系统（IEPS）中，电力推进通常占整个电力负荷的50%。电力推进需要各子系统（发电机，中压配电板，变压器，推进驱动系统，滤波器，中压感应电动机）之间的相互协调[1]。

船舶的电力推进系统设计师们不仅需要深层次地了解各个子系统之间的关系，更需要对全船电力系统和推进驱动系统之间的关系进行深层次的评估，预见极端情况下可能出现的问题和故障。为此，建立推进驱动系统的高效和有效的仿真模型[2]很有必要。本文概述了一种典型的全电力船舶推进系统，并进行了仿真分析。

推进驱动系统的详细仿真是非常有用的，可以让设计师深入了解其工作原理。然而模型复杂性，仿真计算量十分巨大。尤其是全船功率系统仿真，推进系统模型与发电机和其他负载（中压感应电动机和低压总线）相连接的时候，可能导致仿真计算的工作量过大而无法得出相应的仿真结果。因此在电力需求和谐波失真方面需要采用新型的等效简化模型。本文给出了该简化模型并对其进行了相应的分析。

1 推进系统的概述

应用于全电力船舶的最广泛的电力推进系统为基于负载换相逆变器（LCI）的同步电动机驱动系统。该系统的系统框图如图1所示。同步电动机配备了两个30°电角度偏移的三相定子绕组。每个三相绕组由单6脉负载换流晶闸管驱动。双绕组可以减少转矩波动，通过消除5次和7次谐波而提高变频器故障下电机的可靠性。每个LCI通过一个电感器连接12脉冲整流器，该系统由两个晶闸管桥与双绕组变压器连接构成，其中一个为星形连接，另一个为三角形连接。一般来讲，相对于船舶推进负载功率来讲，12脉配置的船舶电网的能力无法满足电能质量的要求。因此，通常采用24脉的电网配置。通过在变压器初级绕组端串联辅助绕组，以实现两个变压器输出端+7.5°和–7.5°相位偏移。

2 系统模型的概述

2.1 仿真模型的建立

图2为LCI同步电动机的结构框图。它由两个控制系统组成，其中一个为电机的速度控制。其通过外部的速度闭环控制和内部的电流闭环控制。另一个通过作用于电机励磁系统完成电机磁通控制。

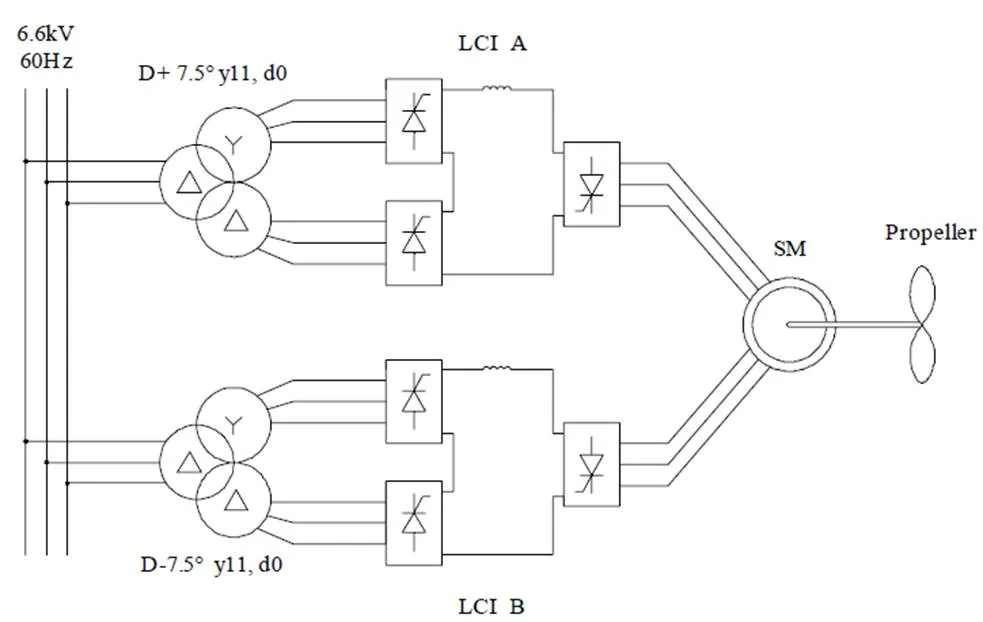
图1 船舶推进系统框图

图3 LCI同步电动机的结构框图

电动机侧变流器由固定的开关角来进行控制。电动机的触发脉冲必须和电动机的反电动势保持同步，其通过计算电机终端的电压完成相应的过程。电压在变流器工作时波动较大，需要经过滤波器的处理。目前存在的问题是低通滤波器会导致频率的相移，导致无法准确监测电动机的转速。滤波器能很好的集成反电动势，最终反应在电机的定子通量上。电动机的终端电压（忽略定子电阻上的电压降）和定子通量同相，触发脉冲和电机通量能有效同步[4]。

本文中采用两个仿真工具：PSIM和Simulink（包括其SimPowerSystems的专用工具包）。基于PSIM和Simulink进行联合仿真，前者主要用于电力电子电路建模，后者主要用于自动化控制的仿真应用。采用PSIM的SimCouple模块，可以支持PSIM和Matlab/Simulink的联合仿真。

变压器、可控硅桥模型和控制系统框图在仿真软件的模型库内均可使用，而对于双定子绕组的同步电动机模型，需要基于原理进行构建。

基于MATLAB平台所建立的9阶非线性双三相电动机的模型接口，可以支持PSIM的应用。由于Matlab库中并没有相应的模型，需要根据电动机统一理论的Park方程在Matlab中构建双三相电动机模型。d-q轴公式变换参考文献[5]。需要注意的是，两个星形绕组的磁耦合参数。本文考虑了典型推进电机的电磁设计，并通过文献[6]中的有限元分析进行了处理，最终得到符合三相定子电路的典型设计。

3 仿真结果

仿真模型完整的反映了推进驱动系统从起始状态，变频器强迫换相脉冲操作，直至转速足够高以使得能够切换到负载换相模式的过程。

推进电动机的转速上升率受发电机的动态性能的限制。如图3所示，显示了电动机转速上升和下降受发电机限制范例，被用来作为仿真的速度模型。

图3 速度斜率曲线

电动机和水中螺旋桨的有关阻力矩方程即为电机转速和船舶的函数方程。根据相应的电动机方程组，阻力矩为其中的一个二次曲线方程式。然而，这是一个静态曲线。因此，它可以被认为电机转速缓慢变化情况的有效近似，因为它并没有考虑船舶速度和马达速度的不同动力学情况。

3.1 推进模式

LCI中可控硅晶闸管之间的电流变化是由电动机反电动势驱动。然而，电动机启动时的反电动势近似为零或非常低，需要采用强迫脉冲的方法。通过切断可控硅晶闸管、直流母线电流的电源，来促使电动机电流为零。然后，直流母线电压恢复以及随后触发可控硅晶闸管。这种情况下，电动机速度从零增加到额定值的10%，这样就可以切换到负载换相操作。

螺旋桨在非常低速的情况下运行时，船舶并不会移动。因此可以使用扭矩和电机速度的静态曲线进行分析。

16极电动机的起动状态的电流波形如图4所示。由于其它相位的变化，可以观察到脉冲电流在方波波形的中间点变为零。约5 s之后电动机的速度达到每分钟15 rpm，变频器被切换到负载换相状态。

电动机起动阶段的推进系统的母线电流曲线如图5所示。其产生的原因是变频器前端为24脉冲。由于脉冲的影响导致仿真算法的计算量很大，降低了仿真效率，并在计算过程中有可能内存不足。但是脉冲操作在船舶电网上影响并不是很大，因为它只在电动机的起动阶段维持短短几秒钟的时间并且馈电流幅值很小。因此，脉冲操作在船舶电网中可以忽略不计，这样可能减少计算量，节省仿真时间，提高仿真效率。

图4 电动机起始阶段的电流波形

3.2 简化模型的描述

根据图3的曲线，电动机速度从50%上升到额定值的速率较为缓慢，因此，可以使用负载转矩的静态曲线进行近似处理。在电动机缓慢的速度变化过程中，机械动力学的部分可以忽略不计，转速和给定相等。这导致电动机模型可以尽速采用R-L-E负载，其中为定子相位电阻，为电机侧的换相电感，为电动机的反电动势的控制电压源。假如电动机的磁通量在任何驱动过程中都是固定的，控制电压的幅值和频率始终和电动机的转速成比例关系。单三相设备中换相电感和d和q电感瞬态分量相等。

R-L-E有源负载通过理想的三绕组变压器连接到两台LCI（即图1中的LCI-A和LCI-B），确切地说其连接到次级星形变压器电路。而两个主变压器电路，由LCI-A和LCI-B提供，分别采用三角形连接方式和星形连接方式。因此，从LCI输出端子来看，变压器和R-L-E有源负载的连接组合可以看成双三相电动机，其中两相移相30°。另外，绕组之间的换相现象的产生原因是理想变压器两个主电路之间的磁耦合。

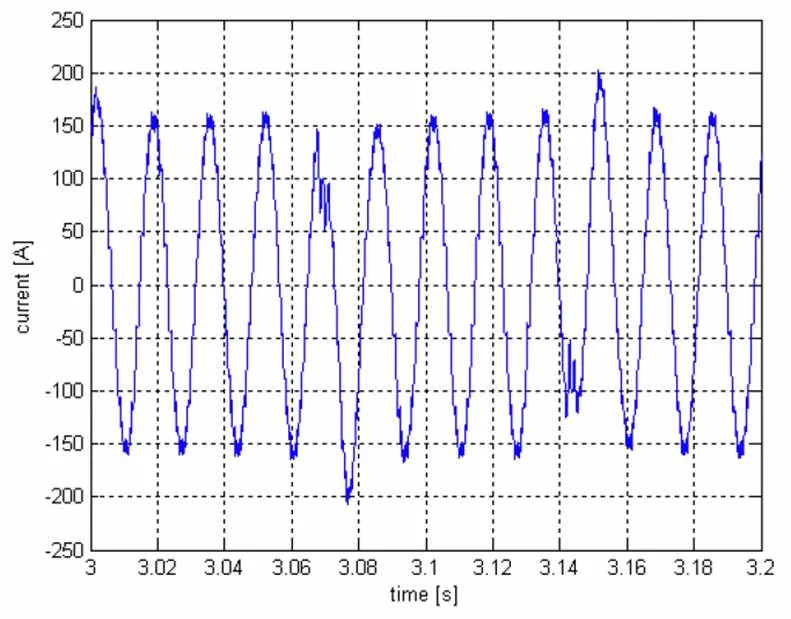
图5 推进系统母线电流

值得注意的是，上述的简化模型并不适合学习电动机状态的电气和机电特性。然而，它已被证明在集中仿真驱动系统和电力系统之间的关系，可以有效减少仿真的复杂程度。

这个结论可以通过比较两组仿真结果来进行证实：一组采用详细的电气和机电特性的双三相电动机模型，另一组采用简化模型。

3.3 详细模型的仿真结果

详细模型的仿真结果显示：电动机电流和母线馈电流随着电机转速变化如图6和图7所示。其中母线电流的THD约为12.9%。

图6 电动机负载换相模式电流（电动机转速≅ 112.5 rpm）

3.4 简化模型的仿真结果

简化模型的仿真结果显示：电动机电流和母线馈电流随着电机转速变化如图8和图9所示。其中母线电流的THD约为12.4%，和详细模型的结果十分近似。

图7 母线电流（电机转速≅ 112.5 rpm）

另一方面，图6和图8之间的比较清楚地表明电动机侧电流波形的变化取决于是采用简化模型还是复杂模型，其中最敏感的参量为与直流母线电流波动相关联的波纹振幅。

4 结束语

本文阐述了典型的全电力船舶的典型推进系统，并构建了推进和负载状态下详细的系统模型，得出了相应的仿真结果。然而，即使采用最先进的PC硬件条件，复杂模型的仿真仍然会导致非常高的计算量，并消耗很长的时间，甚至有可能出现内存不足的问题。由于这个原因，基于对船舶电网影响不大的原则下简化了全船IEPS的仿真模型，即通过用R-L-E负载替代电机模型。并通过对两种模型的推进系统母线电流的幅值和波形进行了分析，证明了简化模型和复杂模型具有良好的一致性。

图8 简化模型的电动机电流（电动机转速≅ 112.5 rpm）

图9 简化模型母线电流（电动机转速≅ 112.5 rpm）

[1] C.G.Hodge, D.J.Mattick and J.O.Flower, “The integration of electrical marine propulsion systems”, in proc. of IEE Int. Conf. on Power Electronics, Machines and Drives, pp.7-11, April 2002.

[2] J.J.Simond, A.Sapin, M.Tu Xuan, R.Wetter and P.Burmeister, “12-pulse LCI synchronous drive for a 20 MW compressor modeling, simulation and measurements”, in proc. of IEEE Industry Applications Society Annual Meeting, Vol.4, pp.2302-2308, October 2005.

[3] R.S.Colby, M.D.Otto and J.T.Boys, “Analysis of LCI synchronous motor drives with finite DC link inductance”, Electrical Power Applications IEE Proceedings-B, Vol.140, No.6, pp.379-386, November 1993.

[4] W.Leonard, Control of electrical drives, Springer, Berlin, 1996.

[5] A.N.Alcaso and A.J.M.Cardoso, “Modeling and simulation of LCI drive system under normal and faulty operating conditions”, in proc. of Portuguese-Spanish Congress of Electrical Engineering, Vol.II, pp.6.157-6.162, July 2003.

[6] A. Contin, A. Grava, A. Tessarolo, G. Zocco, “A Novel modeling approach to a multi-phase, high power synchronous machine”, in proc. of Int. Symposium on Power Electronics, Electrical Drives, Automation and Motion, Sec.19, pp.7-12, 2006.

Modeling and Simulation of Electric Propulsion Systems for All-Electric Cruise Liners

Yang Ming Guo

(Naval Representatives Office of 712 Research Institute, Wuhan 430064, China)

TM728

A

1003-4862（2012）06-0019-04

2014-04-10

杨明国（1966-），硕士，高级工程师。研究方向：机电一体化。