热激励在超声速进气道内对激波诱导的边界层分离的控制机理

严红，王松

（西北工业大学 动力与能源学院，陕西 西安 710072）

热激励在超声速进气道内对激波诱导的边界层分离的控制机理

严红，王松

（西北工业大学 动力与能源学院，陕西 西安 710072）

通过数值模拟的方法研究了马赫5的超声速进气道内，热激励对激波／边界层相互作用的控制机理。研究了热激励器放热功率（E）、热激励器展向放置数目（N）和热激励器到控制激波的距离（S）三个参数在超声速进气道内激波控制和边界层分离改善中的表现。分别针对以下四种条件进行了数值模拟：1）E＝2kW、N＝2、S＝0．02m；2）E＝3k W、N＝2、S＝0．02m；3）E＝2k W、N＝3、S＝0．02m；4）E＝2k W、N＝2、S＝0m。分析发现：在以上四种条件下，均可观察到热激励在控制激波和改善激波诱导边界层分离上有着显著的效果。热激励器的放热功率对激波的控制效果有着明显的影响，在本文所考虑的热激励能量范围内，放热功率越大，原激波角的改变越大，最终分离区的改变越明显；展向放置的热激励器数目N影响着输入到流场的能量密度，并且N越大，壁面附近的激波面越趋于平面。尽管N对上壁面沿展向的压力分布无明显影响，但对上壁面分离区大小有明显的影响；对比条件1和4下的计算结果，发现S＝0．02m可以得到很好的控制效果，而S＝0m时流场结构几乎没有变化，这就表明热激励器必须放置在控制激波上游的一定距离处才会有预期的效果。

热激励器；激波控制；边界层分离；超声速进气道；流动控制

0 引 言

激波／边界层的相互作用是一个古老而有充满活力的课题。早在1939年，Eerri［1］就开始了最早的机翼在高声速风洞试验中发生边界层分离的实验研究，而到了1947年，Howarth［2］最先尝试了关于激波与边界层干扰的理论研究。在超声速气体流动中，激波／边界层干扰是随处可见的，以至于人们对激波边界层的研究一直持续了60多年，当然随着人们对该问题的认识不断加深，到目前为止大多数人已经把工作重点从激波边界层干扰机理的研究转移到寻求改善激波边界层相互以及提高流场气动性能的方法上，而且目前乃至以后寻求高效的激波边界层流动的控制方法将变得尤为重要［3-5］。在具有超声速飞行能力的飞行器中，大都采用边界层气流吹除和加入特定的扰流设备［6-9］对进气道内存在着的激波边界层干扰进行控制，通常的方法是采用附面层泄除装置、分流器、边界层吹除控制、旋涡发生器控制、空腔循环控制、中央阻力片控制、流向狭槽控制和微射流控制等。实际应用表明这些技术是行之有效的，但是边界层中放置特定的扰流设备将增加飞行器的阻力、重量和费用；而且抽吸边界层、边界层吹除和微射流控制需要繁琐的管路，占用了宝贵的空间，增加了飞行器的重量和价格。

壁面放电作为一种流动控制技术已经在理论和实验上得到证实可以用来提高超声速喷管和超声速近壁面流动的气动性能，例如减小阻力［10］，控制流动分离［11］，改变进气道内的激波结构［12］以及提高燃烧室内燃气的混合度［13］。基于壁面放电的流动控制机理主要有两大类：一类是基于磁流体动力学和电流体动力学的观点，认为其控制效应是非热效应。另一类基于放电产生的焦耳热加热气流的观点，认为其流动控制机理主要是热效应。基于热效应理论，通过在预定的位置进行表面放电产生等离子体可以给流场注入能量，等离子体层能够改变边界层特性，因此，流场参数如马赫数、压力和激波位置及强度都能发生可控的改变［14］。Samuel等［15］通过实验的方法研究了直流放电等离子体对斜激波的影响效果，其结果显示直流放电等离子体可以对斜激波产生一定的改变。Leonov和Yarantsev［16］通过小型喷管验证了壁面放电的流动控制特性，分析实验结果证实了壁面放电可以作为一种激波控制的方法，并且发现激波控制的效果与输入的能量有关。Webb等［17］通过实验研究了壁面放电对激波诱导的边界层分离的控制机理，结果显示壁面放电对激波和边界层分离的控制机理主要为热效应，边界层内放电加热导致边界层特性改变，近一步影响到整个流场。Yan［18］对马赫2的超声速进气道内壁面放电激波控制进行了数值模拟，结果显示热激励可以改变激波结构，并且在一定范围内，热源能量越大，激波改变越明显。通过热激励器控制入射激波，改变入射激波强度和入射点，从而改善激波与边界层干扰的强度，减弱边界层分离，也是边界层分离控制的一种可行方法。

壁面放电超声速流动控制过程包含了十分复杂的物理过程，从目前的数值模拟技术来看，没有一种成熟的模拟方法，大多数的研究仅停留在实验方面，数值模拟也是从唯像的角度出发。本文以一种简化的模拟手段，将等离子体的加热效应用热激励器来替代，通过研究热激励器的放热功率E、热激励器展向放置数目N和热激励器与控制激波的流向距离S三个重要参数，来说明壁面放电对激波控制和边界层分离改善的影响。计算结果验证了壁面放电加热可以作为一种控制激波与边界层干扰的有效方法。本文可以为工程应用提供一定的指导。

1 数值计算过程

1.1 计算条件的设置

根据飞行走廊图，一个吸气式飞行器能以马赫数5的速度在15kg的高度飞行。在此，马赫数为5的带有混合压缩进气道的飞行器的来流条件，可以采用15kg高空处的气流参数，其静压p∞＝1．2×104Pa，静温T∞＝200K。如图1所示是一个长0．3m、入口高0．06m、展向宽0．018m的超声速进气道计算模型，进气道的下壁面中段由两个相邻的斜坡面组成，这两个坡面与水平面的夹角分别为7°和14°，图1中红蓝两条线分别表示两个压缩角产生的斜激波。

我们利用有限体积法求解加入热源项的三维非定常Navier-Stokes方程，假设气体为理想气体，粘性模型采用SST湍流模型，计算粘性与温度的关系用Sutherland插值公式。时间精度采用二阶隐格式，时间步长选择为10-7s，空间精度采用三阶MUSCL（Monotonic Upwind Scheme for Conservation Laws）格式［19］，通量项离散采用AUSM（Advection Upstream Splitting Method）格式。壁面条件采用绝热无滑移壁面条件，入口边界给定马赫数、总温和总压，出口边界采用一阶外插格式。展向边界条件选为对称边界条件。

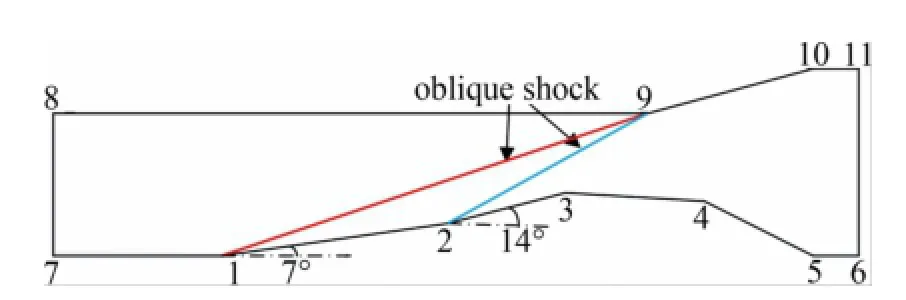
图1 马赫5进气道平面结构简图Fig.1 Geometry of the Ma＝5 supersonic inlet

对于热激励器的模拟，我们采用简化的数学模型，在能量方程中添加热源项来模拟热激励器的加热效应，热源项大小由激励器的放热功率以及等效热源尺寸决定：

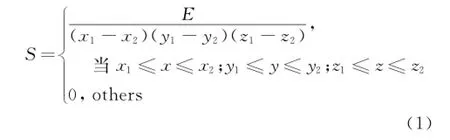
其中x1、x2、y1、y2、z1、z2等参数是图2中等效热源1的位置及尺寸参数。在计算流场中加入N个功率为E（k W）、长0．02m和截面为0．003m×0．003m的长方体热源，热源位于控制激波上游S（m）处，并且沿进气道展向等间距放置。如图2所示，1为热激励器的有效作用区域，2为压缩坡面，3为上壁面。

图2 热激励器在进气道内的布局图Fig.2 Layout of thermal actuator in the inlet

1.2 计算网格

计算网格如图3中所示，选择了三种网格进行网格相关性的研究。在y方向网格数分别为60、90和120并且双向拉伸，拉伸比均r＝1．04，在x和z方向网格数固定，分别为388和36且均匀分布。在图3中，图3（a）的区域包含有加热区以及热激励的诱导激波产生位置。图3（b）的区域含有入射斜激波与边界层相互干扰区以及上壁面处存在的边界层分离区。因此，在这两个区域进行了网格加密。网格特点是：x方向网格均匀分布，y方向靠近壁面处网格变密，远离壁面的网格较疏。

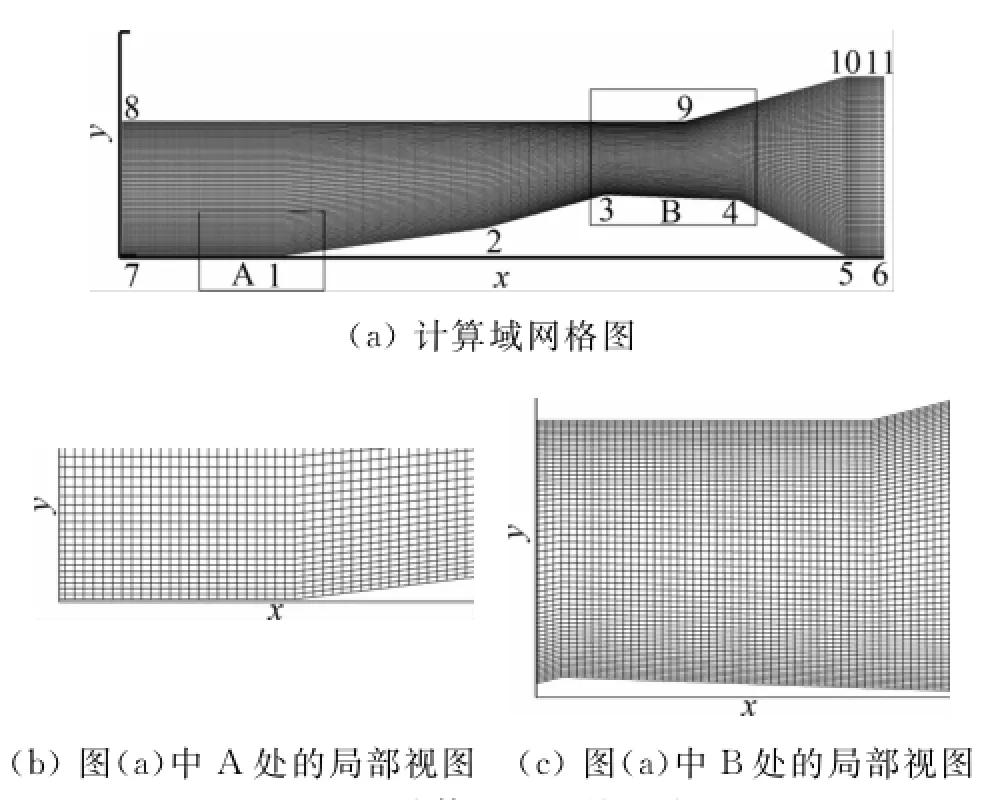
图3 计算所采用的网格Fig.3 Grid of computation

图4（a）给出了不同网格数下下壁面压力分布曲线，并且与无粘的理论解进行了对比，其中压力值通过来流静压进行无量纲化处理。图4（b）可以看出，由于粘性的影响，入口处上壁面存在边界层诱导的弱斜激波，由于该激波入射在第二个斜坡面上，这样会使下壁面的第二个斜坡面上入射点下游的压力增大。因此，数值计算与无粘理论解的结果在第二道激波后有明显的差别，然而其他区域的差别相对来说较小。可以看出三种网格的下的壁面压力差别很小，综合考虑最终选择第二种网格作为接下来的计算网格。

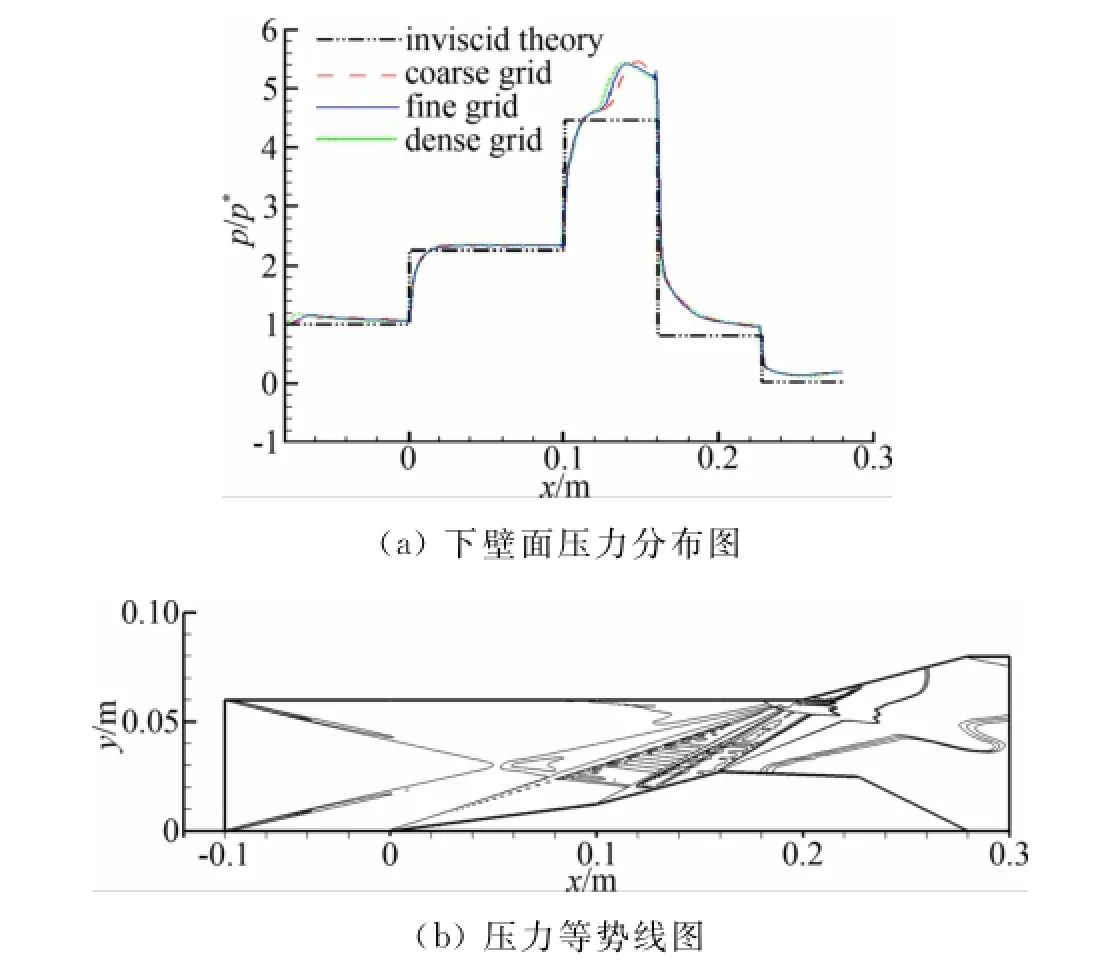
图4 无粘理论解和数值解的对比Fig.4 Comparison of theoretical value with numerical solution

2 数值计算结果及分析

2.1 不加热源的计算结果

对马赫5超声速进气道内的流场进行了数值模拟，得到进气道内流场结构如图5所示。图5（a）显示了中心面上的压力云图（压力已经通过来流静压进行无量纲处理），可以清晰地看出，第一道压缩面产生的斜激波在上壁面与边界层作用后，导致边界层内很高的逆压梯度，并且该激波反射后与第二压缩面产生的激波相交，交点后产生局部高压区。图5（b）显示了中心面上的x方向速度云图（速度已经通过来流速度进行无量纲处理），可以清晰地看出，在上壁面由于激波与边界层相互作用导致了边界层的分离，在该区域内存在回流。图5（c）显示了中心面上的数值纹影图，可以清楚地看流场中激波的结构以及激波在边界层反射后又与其它激波相互作用的情况。

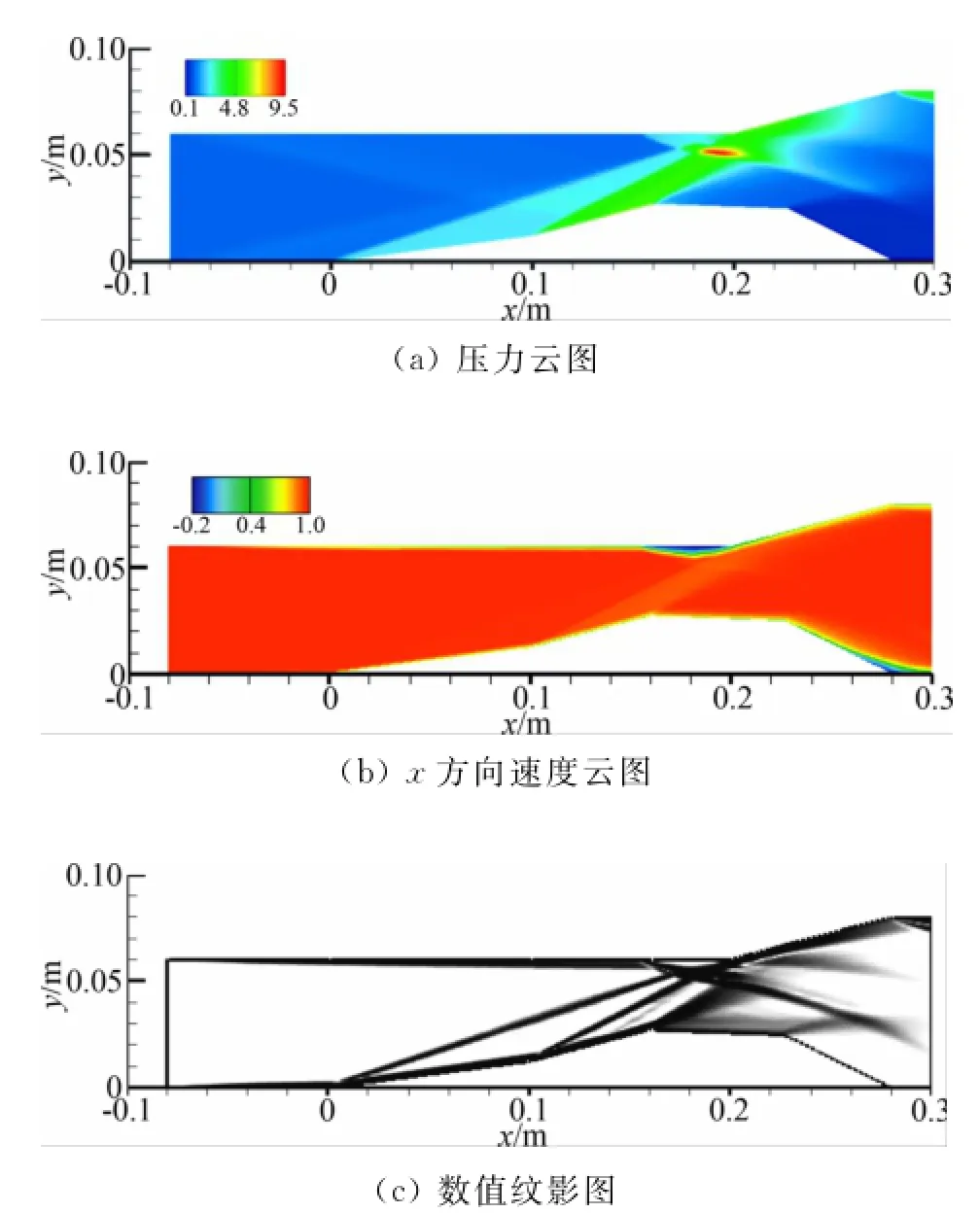
图5 没有热源时中心截面（z＝0.009m）上的计算结果Fig.5 Result on the center plane

2.2 E＝2k W、N＝2、S＝20mm时计算结果

为了与加热的计算结果进行对比，图6展示了加热方式为E＝2k W、N＝2、S＝0．02m的计算结果。图6中的（a）～（c）分别与图5中的（a）～（c）对应，对比可以清楚地发现加入热源后流场中激波被改变及上壁面边界层分离区减小。

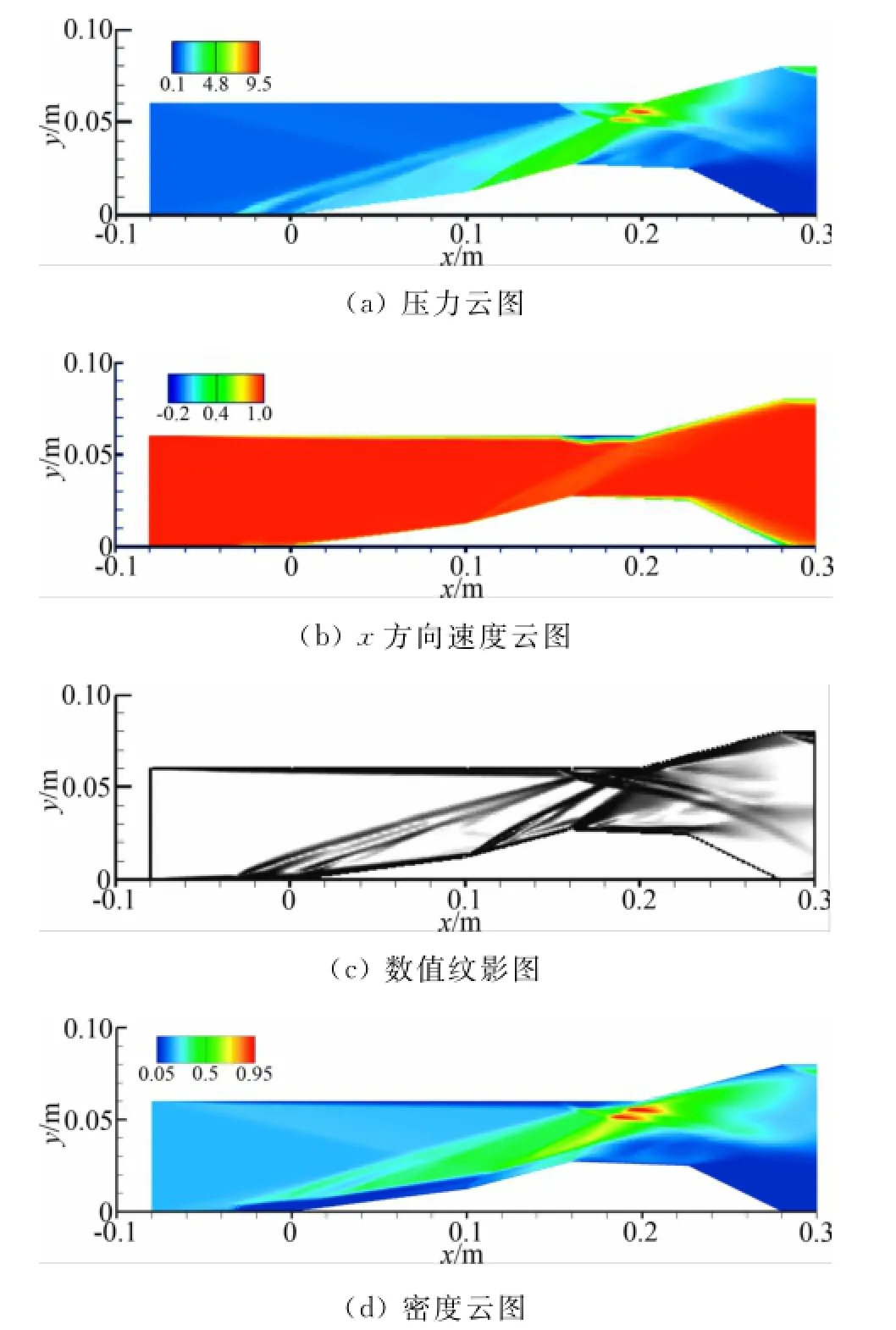
图6 加入热源时中心截面（z＝0.009m）上的计算结果Fig.6 Result on the center plane with E＝2kW，N＝2 and S＝0.02m

图6（a）和（c）中可以看到在热激励处会产生一道斜激波，这道激波相比于已有的斜激波，其强度较弱。由图6（d）可看到下壁面边界层受热变厚，减小了第一压缩角的真实压缩角度。热激励器对流场的影响在于：1）产生诱导激波，并入射在上壁面的边界层上，由于这道诱导激波强度小，很难使边界层产生分离，气流经过热激励的诱导激波后马赫数降低，因此会使得原始激波强度降低。2）加热边界层，使得边界层内气流密度降低，边界层厚度增大，由于边界层内有贴近壁面部分为亚声速流动，激波只能产生于边界层中的超声速流动区域，边界层变厚意味着亚声速区域增大，这样就会改变斜激波的产生位置，使得原始激波的起始位置发生了改变，在不考虑激波角改变的情况下，原始激波在上壁面的入射点也相应发生改变，最终改变上壁面边界层内的压力分布。在以上两个因素共同作用下，原本入射到边界层上的强激波被减弱了，因而达到了控制边界层分离的目的。

下面我们将定性分析三个重要参数（E，N和S）对激波控制的影响规律。表1列出了四种不同的加热方式。通过两两对比来探索这三个参数的作用。

表1 四种不同的热源添加方式Table 1 Four different heat source

2.3 热源功率E的影响

对比算例1和2，两种热激励的主要区别是加热功率不同。图7展示了在两种功率下流场中诱导激波和原始激波的形状和位置。

图7（a）表示两种功率下诱导激波的结构，可以看出E＝3kW的激波角大于E＝2k W的激波角。图7（b）表示两种不同功率下原始激波的形态和位置，并且与没有热激励器时的原始激波位置进行对比，发现热激励器可以使原始激波的激波角增大，并且E＝3k W时对应的激波角大于E＝2kW的激波角。激波角大小不同就会导致在上壁面入射位置不同，因而就会影响激波边界层相互作用的效果。

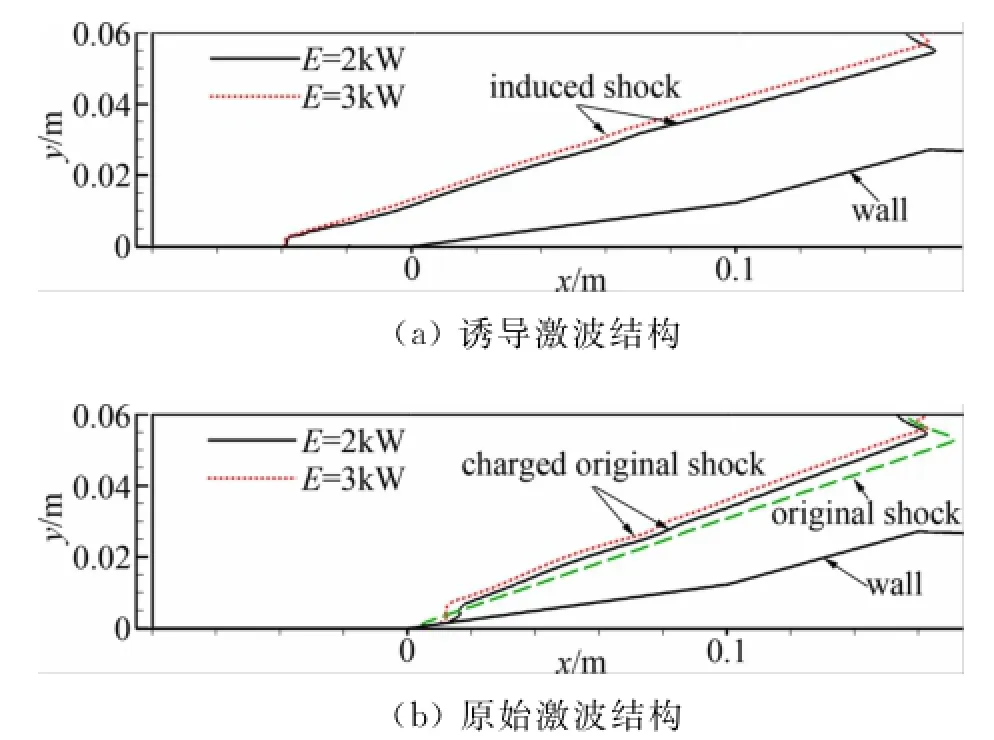
图7 两种功率下流场中的激波结构图Fig.7 Shock wave structures under two different input power

下面就来仔细观察上壁面处激波和边界层的相互作用。图8展示进气道上壁面处激波与边界层干扰区的流线图和压力等势线图，可以看到图8（a）中有较大的分离区，图8（b）的分离区较小，边界层分离区的大小很大程度上体现了边界层内逆压梯度的大小。而边界层内部压力分布很大程度上是由外流的压力分布决定，在本问题中外流的压力分布直接受制于激波的位置，因为激波前后压力发生突增，会带给边界层很大的逆压梯度。图8（a）中的20000Pa的压力等势线与24000Pa和28000Pa等势线之间的距离相比图8（b）中较小，说明图8（a）中该区域的压力梯度较大，故其对应的边界层分离区较大。这一点可以从诱导激波与原始激波在上壁面的相对位置中得到解释。

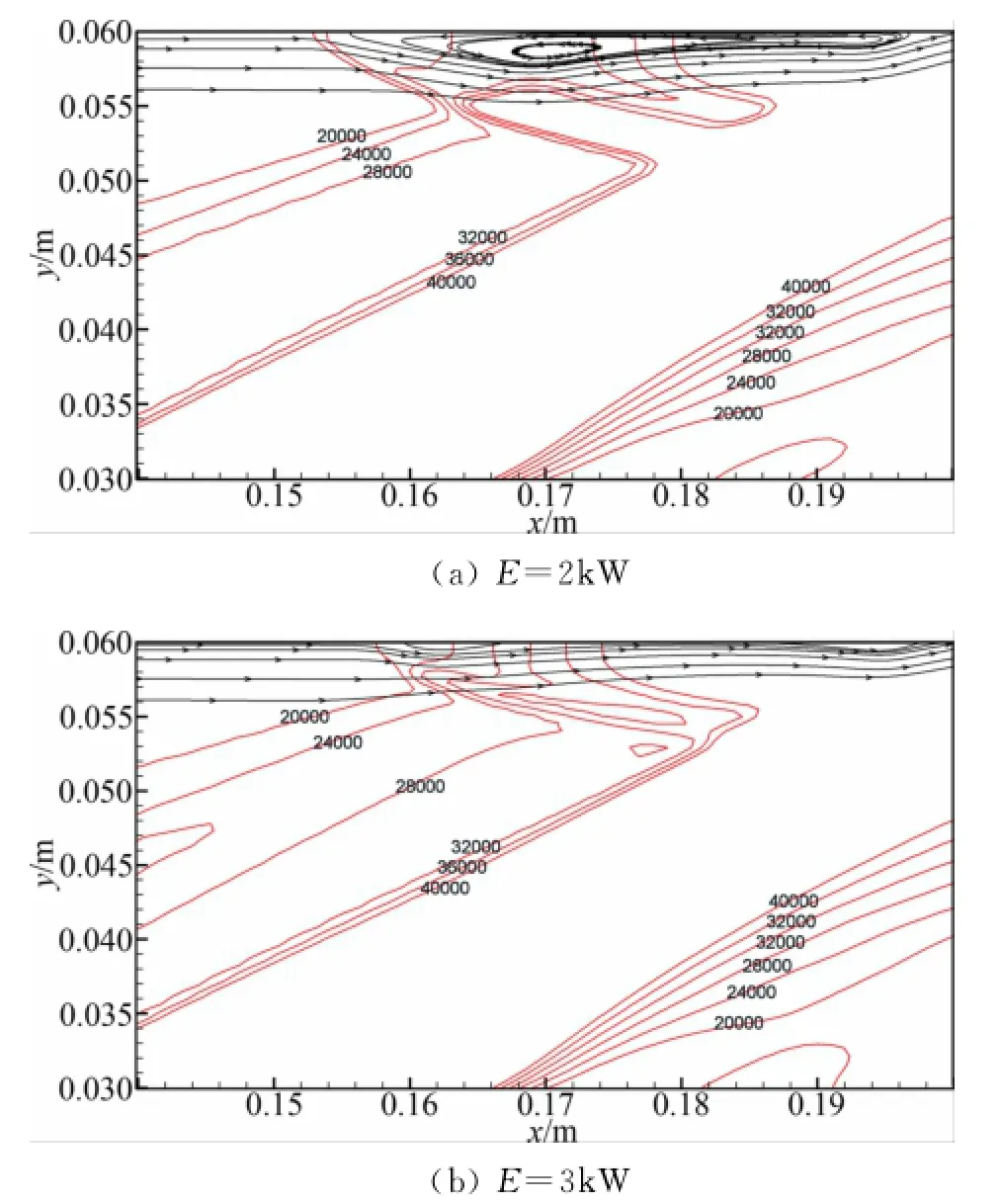
图8 中心截面（z＝0.009m）上压力等势线和流线图Fig.8 Pressure contour line and streamline on the center plane

表2中分别给出了2k W和3k W的热激励器诱导斜激波以及原始激波在上壁面边界层的入射点坐标。其中x1是原始激波在上壁面边界层入射点的坐标，x2是诱导激波在上壁面边界层上入射点的坐标。E＝2k W时产生了很大的分离区而E＝3k W时产生的分离区很小，其中主要原因是3k W时产生的激波没有与第一压缩面上产生的激波在上壁面附近相交（由表2可以看出E＝3kW时Δx值较大），故而入射在边界层上是两个较弱的斜激波，因此不能产生很大的逆压梯度。而E＝2k W时产生的激波恰好与第一压缩面上产生的激波在上壁面边界层附近相交（由表2可看出E＝2k W时Δx值很小），这样会产生更强的斜激波，因此其入射到边界层的激波强度很高，就会产生很高的逆压梯度，故其边界层分离区很大。

表2 两种功率下的激波位置参数Table 2 Shock wave position parameters under two different input power

2.4 热激励器展向放置数目N的影响

对比算例1和3，两者区别在于展向热激励器数目的不同。发现热激励器数目对放热区域的激波面形状有很大的影响。图9展示不同N下20kPa压力等势面图，从热激励区压力等势面图的外形可以看出，3个2k W的加热方式要比2个2k W在热激励区的压力等势面更加均匀，而在远离加热区后两者均又恢复为平面。

图9 p＝20kPa的压力等势面图Fig.9 Pressure isosurface at p＝20k Pa

图10给出了上下壁面的压力分布云图，其中压力值经过来流静压值进行无量处理，可以看出下壁面Z方向的压力分布与N关系密切，当进气道高度足够高时，上壁面Z方向的压力分布不会受到下壁面Z方向压力波动的影响。随着N的增大，下壁面Z方向的压力分布趋于均匀并且压力值增大，故诱导激波增强以及诱导激波角和原始激波角的角度增大，上壁面入射点位置发生变化。对比图10（a）和图10（b）发现N可以影响到原始和诱导激波在上壁面的入射位置，因此会在改善边界层分离中起到作用。

2.5 热激励器与控制激波距离S的影响

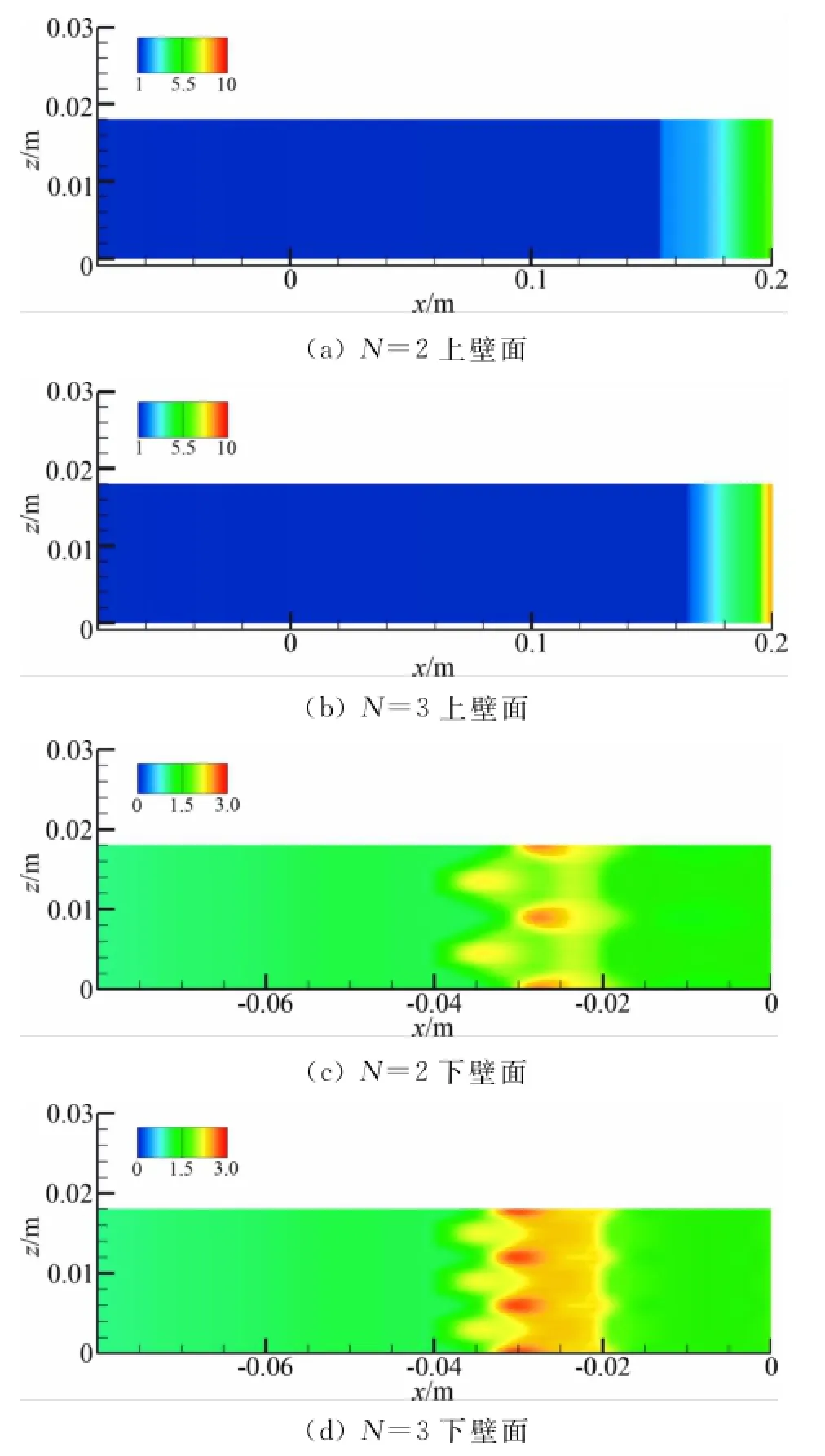
图10 上下壁面上的压力云图Fig.10 Pressure contours at the top and bottom walls

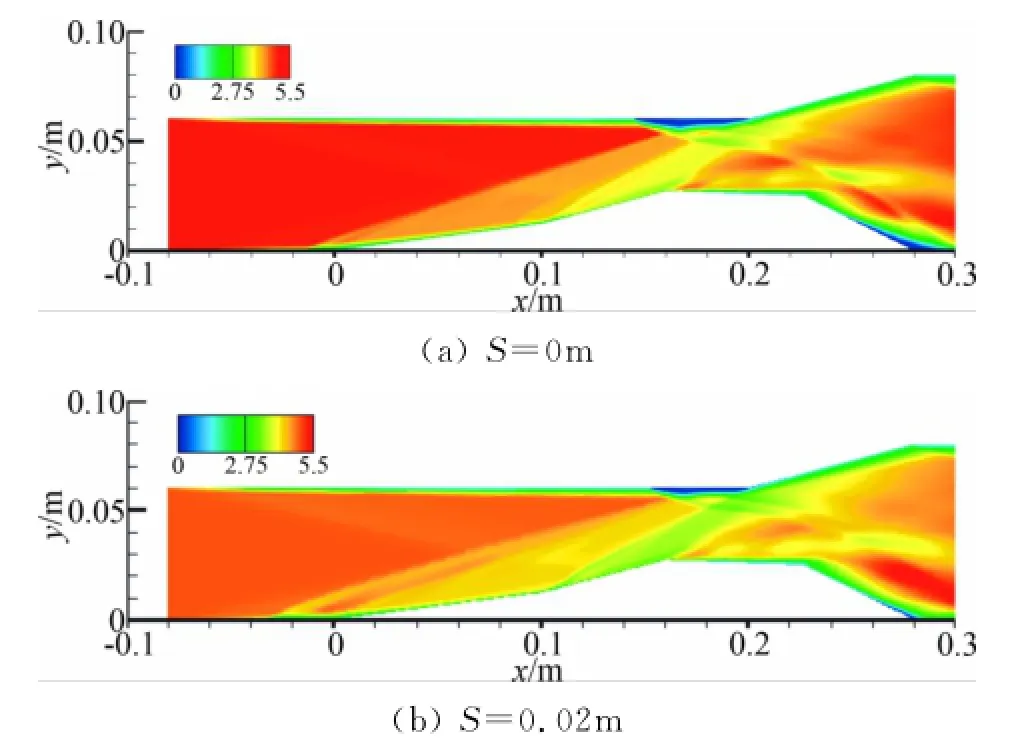
图11 中心截面（z＝0.009m）上马赫数云图Fig.11 Mach number contours on center plane

对比算例1和4，两者区别在于热源沿流向放置于第一压缩角前的距离不同。图11为马赫数云图。将图11（a）和图11（b）进行对比，发现S＝0m的结果相比于S＝0.02m，对流场的改变很小，这是因为S很小时，热源提供的热量还没来得及加热斜激波前的边界层就被吹到激波下游了，这样热激励的效果就不显著，因此为了达到理想的控制激波边界层干扰的效果，热激励器必须放在控制激波的上游，但保持一定的距离。

图12为S＝0m时的激波边界层干扰区域压力等势线图，由于等势线p＝20k Pa和p＝28k Pa之间的距离非常小，可以看出入射激波的强度很大，激波前后压力差很大，反应在边界层区域就是逆压梯度非常大，会导致明显的流动分离。

图12 中心截面（z＝0.009m）上压力等势线和流线图，S＝0mFig.12 Pressure contour line and streamline on center plane

3 结论与展望

本文对马赫5的超声速进气道内热激励器控制激波和边界层分离的过程进行了数值模拟，结果显示热激励可以改变流场结构，起到降低入射激波强度以及减小分离区大小的作用。

文中分别计算了以下四种热源添加方式：1）N＝2、E＝2k W、S＝0．02m；2）N＝3、E＝2k W，S＝0．02m；3）N＝2、E＝3k W、S＝0．02m；4）N＝2、E＝2k W、S＝0m。结果发现：

1）热激励器不同的放热功率，引起了激波改变和边界层分离的不同变化幅度。从计算结果看出：放热功率越大，诱导斜激波的角度越大，激波强度也就越大，原激波的激波角改变量越大，原始激波强度减弱越明显，上壁面的分离区也就越小。

2）热激励器展向放置数目N越大，输入到流场的能量越密集。热激励器展向放置数目N越大下壁面沿展向的压力分布越均匀，下壁面边界层上方的激波面（诱导激波和原始激波）越趋于平面。从上壁面压力分布云图可看出：N越大，诱导激波就越强，原始激波改变也越明显。

3）在相等的热源数和热激励功率条件下，S＝0．02m时要比S＝0m时对激波改变明显得多，而S＝0m情况对流场的改变很小，因为S很小时热源提供的热量还没来得及加热斜激波前的边界层就被吹到激波下游了，所以热激励的效果就不能实现，因此热激励器必须放置在控制激波的上游一定距离。

四个计算结果均可以观察到激波结构和激波诱导边界层分离的改变。热激励器对流场的影响在于，首先在热激励器处会产生的诱导激波入射在上壁面的边界层上，由于这道诱导激波强度小，很难使边界层产生分离，气流经过热激励的诱导激波后压力升高、马赫数降低，因此在其它条件不变的情况下会使得原始激波强度降低；其次热激励器加热边界层，使得边界层内气流密度降低，边界层厚度增大，由于边界层内部含有亚声速流动，激波只能产生于超声速流动区域，边界层变厚就会改变斜激波的产生位置，使得原始激波的起始位置发生了改变，在不考虑激波角变化的情况下，原始激波在上壁面的入射点也相应发生改变，最终改变上壁面边界层内的压力分布。在以上两个因素共同作用下，原本边界层内强逆压梯度被降低了，最终导致了在上壁面由于入射激波引起的边界层分离区减小，因而达到了控制边界层分离的目的。

［1］EERRI A．Experimental results with airfoils tested in the high speed tunnel at guidonia［J］．National Advisory Committee for Aeronautics Technical memorandum，1939．11（17）：946．

［2］HOWARTH L．The propagation of steadydisturbances in a supersonic stream bounded on one side by a parallel subsonic stream［J］．Proe．Cambridge Phil．Soe，1947，44（1）：380-390．

［3］DAVID S D．Eifty years of shock-wave／boundary-layer interaction research：what next？［J］．AIAA Journal，2001，39（8）：1517-1531．doi：10．2514／2．1476

［4］YUAN X J，TU G H，ZH ANG H X，et al．Disturbance waves evolvement influenced by shock-boundary interaction［J］．ACTA Aerodynamica Sinica，2006，24（1）：22-27．（in Chinese）

袁湘江，涂国华，张涵信，等．激波边界层的相互作用对扰动波传播的影响［J］．空气动力学学报，2006，24（1）：22-27．

［5］TIAN Z Y，LI H，EAN X Q．Numerical investigation for six types of hypersonic turbulent shock-shock interaction［J］．ACTA Aerodynamica Sinica，2004，22（3）：361-364．（in Chinese）

田正雨，李桦，范晓樯．六类高超声速激波-激波干扰的数值模拟研究［J］．空气动力学学报，2004，22（3）：361-364．

［6］TINDELL R，WILLIS B．Experimental investigation of blowing for controlling oblique shock／boundary layer interactions［R］．AIAA Paper 1997-2642．doi：10．2514／6．1997-2642

［7］JENKINS L，GORTON S，ANDERS S．Elowed controldevice evaluation for an internal flow with an adverse pressure gradient［R］．AIAA paper 2002-266．doi：10．2514／6．2002-266

［8］SERGE E T，PADUANO J D．Elow control in a transonic inlet［R］．AIAA Paper 2006-3883．

［9］REN S X，LI X L，GUO R W．Embedded inlet flow control researching［J］．ACTA Aeronautica Et Astronautica Sinica，2000，21（3）：226-229．（in Chinese）

任三星，李学来，郭荣伟．埋入式进气道流场控制研究［J］．航空学报，2000，21（3）：226-229．

［10］SH ANG J S，SURZHILOV S T，KIMMEL R，et al．Mechanisms of plasma actuators for hypersonic flow control［J］．Progress in Aerospace Sciences，2005，41（1）：642-668．doi：10．1016／j．paerosci．2005．11．001

［11］CORREALE G，POPOV I B，RAKITIN A E，et al．Elow separation control on airfoil with pulsed nanoseconddischarge actuator［C］．49th AIAA Aerospace Sciences Meeting，Orlando，Elorida 2011：1079．doi：10．2514／6．2011-1079

［12］SERGEY MACHERET，RICHARD MILES，MIKHAIL SHNEIDER．Magnetohydrodynamic and electrohydrodynamic control of hypersonic flows of weakly ionized plasmas［J］．AIAA Journal，2004，42（7）：1378-1387．doi：10．2514／1．3971

［13］STARIKOVSKAIA S M．Plasma assisted ignition and combustion［J］．Topical Review，Journal of Physicsd Applied Physics，2006，39（16）：265-299．DOI：10．1016／j．pecs．2012．05．003

［14］SAMUEL M，ELKE P，PETER P．Shock wave control by non equilibrium plasma in cold subsonic gas flows［R］．AIAA Paper 2000：23-27．

［15］SAMUEL M，IGOR V，et al．Study of oblique shock waves in weakly ionized nonequilibrium plasma［R］．AIAA paper 1999-4823．

［16］LEONOV S，YARANTSEV D．Near-surface electricaldischarge in supersonic airow：properties and flow control［J］．Journal of Propulsion and Power，2008，24（6）：1168-1181．

［17］WEBB N，CLIEEORD C，SAMIMY M．An investigation of the control mechanism of plasma actuators in a shock wave-boundary layer interaction［C］．51st AIAA Aerospace Sciences Meeting including the New Horizons Eorum and Aerospace Exposition．AIAA paper 2013-402．doi：10．2514／6．2013-402

［18］YAN H．Near-surfacedischarge in supersonic inlet control［C］．51st AIAA Aerospace Sciences Meeting including the New Horizons Eorum and Aerospace Exposition．AIAA paper 2013-530．doi：10．2514／6．2013-530

［19］MA M S，DENG Y Q，ZHENG M，et al．Numerical investigation of supersonic jet interactions for tactical bodies［J］．ACTA Aerodynamica Sinica，2007，25（4）：468-473．（in Chinese）

马明生，邓有奇，郑鸣，等．超声速侧向多喷流干扰特性数值模拟［J］．空气动力学学报，2007，25（4）：468-473．

Control of shock／boundary layer interaction in supersonic inlet using thermal excitation

YAN Hong，WANG Song
（School of Power and Energy，Northwestern Polytechnical University，Xi＇an 710072，China）

A numerical study was performed to investigate the effects of thermal excitation using surfacedischarges in Mach 5 supersonic inlet by solving the unsteady Navier-Stokes equations．Three parameters，including the input power of thermal actuators（E），the number of thermal actuators（N）and thedistance between actuator to the first compression corner，were used to study their effects on the control of shock wave and improvement of boundary layer separation．Eour cases，which include 1）E＝2k W、N＝2、S＝0．02m；2）E＝3k W、N＝2、S＝0．02m；3）E＝2k W、N＝3、S＝0．02m；4）E＝2k W、N＝2、S＝0m，were considered．Erom the results for all four cases，it can be observed that the thermal excitation shows significant effect on the control of shock wave and improvement of boundary layer separation induced by shock wave．The heating power of thermal actuator has obvious effect on the control of shock wave．Within the scope of thermal excitation energy considered in this paper，the greater heating power，the greater change of the original shock wave angle，and finally the more obvious change of the separation．The number of thermal actuatorNalong the spanwisedirection affected the energy intensity that input to the air flow．The greaterN，the flatter the shock wave surface near the wall．Although the numberNdid not have significant effect on the spanwisedirection pressuredistribution of the upper wall，but it had obvious effect on the size of separation on the upper wall．Comparison between cases 1 and 4 showed that theS＝0．02m can get a very good control effect，and theS＝0m had little effect on the flow structure．This indicated that the thermal actuator must be placed upstream of the control shock with a certaindistance．

thermal actuator；shock wave control；boundary layer separation；supersonic inlet；flow control

V211.3

Adoi：10.7638／kqdlxxb-2013.0102

0258-1825（2014）06-0806-08

2013-10-28；

2014-04-03

严红（1969-），女，江苏邗江人，教授，博士，研究方向：超声速流动．E-mail:yanhong＠nwpu.edu.cn

严红，王松．热激励在超声速进气道内对激波诱导的边界层分离的控制机理［J］．空气动力学学报，2014，32（6）：806-813．

10．7638／kqdlxxb-2013．0102 YAN H，WANG S．Control of shock／boundary layer interaction in supersonic inlet using thermal excitation［J］．ACTA Aerodynamica Sinica，2014，32（6）：806-813．