基于CAPM模型的电子商务上市公司系统风险分析

谭崇桦?邓静?张敏?黄李明?李敏

[摘 要]本文选取20家电子商务上市公司为样本，在β值和R2值的基础上分析了电子商务上市公司的系统风险以及其系统风险占总风险的比例。通过运用数理统计法和文献资料法，对电子商务上市公司的系统性风险进行分析研究。系统分析显示样本公司个股的波动幅度比大盘的波动幅度小，个股风险较低。电子商务上市公司的系统风险占总风险的比例偏低，电子商务上市公司的风险主要由公司基本面的非系统风险组成。本文旨在分析电子商务上市公司的系统风险，通过搜集数据并加以计算、分析，为电子商务上市公司的投资者提出建议，以此来加快我国虚拟经济的发展速度。

[关键词]电子商务上市公司；系统风险；CAPM模型；β系数

对资产定价模型的检验有很多，涉及的专业领域也比较广泛。目前为止贝塔系数在一些领域被验证是遵循均值回归过程的。本文认为电子商务的系统风险的的贝塔系数遵循了均值回归趋势的原理，通过计算长期均值和标准差，来分析电子商务上市公司的系统风险，希望能为内外部关联人员提供一些参考。

一、研究方法

CAPM理论是现代金融学的重要基石，该模型是在严格限定条件下单期静态对投资组合的最优求解，它对资产收益和风险关系给出了精确的分析与预测。如果在均衡的资本市场下，股票i的收益率是R，我们可以得出以下公式：E（ri）=rf+βi[E（rm）-rf]，式中E（ri）为第i种资产的期望收益率；E（rm）为市场组合的预期收益率；rf为无风险收益率；βi为第i种资产的风险或β系数。βi=σim/σm2

σm2是市场组合收益率的方差，σim是股票i收益率与市场组合收益率的协方差；βi即为股票i的β值。

二、样本选择和模型设计

样本选择。根据南方财富网和同花顺网提供的电子商务上市公司 ，本文从中选取了20家公司作为样本。其中14家为电子商务公司，涵盖了医药、纺织、综合等多个行业；另外6家為电子商务软件公司 。这些电子商务公司多为本行业具有代表性的公司，这些样本公司能反应本行业特征，体现电子商务公司的风险。

本文选取了2013年12月9日-2014年12月8日期间各股票的交易日数据，用来避免因为样本的数量太少而导致beta系数出现误差的情况。又由于这20支股票分别来自上海证券交易所与深圳证券交易所，因此本文取上证综指与深成指作为日收盘指数。另外，本文亦借助了计量经济学软件Eviews求得所需数据。

变量选取与计算方法。本文的股票收益率选取了对数收益率。因为根据相关金融研究的结果证明，对数差分收益率更符合股票收益率的实际情况，所以在处理股票收益率数据的时候普遍倾向于使用㏑。而且，使用“㏑”处理数据能使数据更加平滑，克服数据本身的异方差。因为本文用到了线性回归模型，若线性回归模型的数据存在异方差性，那么用传统的最小二乘法求得的参数估计量也不是有效估计量了，此时就无法对模型参数进行相关的显著性实验。此外，对数收益率相比于百分比收益率而言前者更接近正态分布，而计量经济学的多数计量方法均基于随机变量服从正态分布的假设。如本文用到的普通最小二乘法的基本假设中就包括随机干扰项的正态假设。

（1）股票日收益率：Rit=lnPit-lnPit-1。

（2） 同期各种股票所在市场的收盘指数的日收益率：Rt=lnPt-lnPt-1，Rt 为样本中某公司股票所在证券交易市场在t观察日的指数日收益率，Pt为该证券交易市场t观察日的日收盘指数。

模型设计：CAPM模型的假设条件是：投资者是完全理性的，并且证券市场是完全有效和充分竞争的。在此基础上，CAPM模型有3点重要含义：一，以β系数来衡量股票系统性风险，β系数越大，系统性风险越大，反之，亦然。二，一支股票或者股票组合的预期收益率会是线性函数，当股票处于均衡的时候。三，系统性风险改变股票价格。风险分为系统风险和非系统风险，非系统风险主要是由公司特质引起的，我们可以通过持有充分风险的股票组合而使风险趋于零。因此我们主要就是对对电子商务上市公司的系统风险进行分析：一是电子商务上市公司系统风险大小的程度，二是在风险中，系统风险的比率。

构建CAPM模型的方程：Rit=ai+βiRmt+εit

Rit表示第i个样本股的收益率，Rmt为市场收益率，ai为线性方程的截差距，βi为线性方程的斜率，εit为误差项，即实际收益率与预期收益率的偏差。斜率βi度量股票i对市场的敏感程度。

在此说明，因为我国利率还没有达到完全市场化的程度，因此不同于国外采用3个月的短期国债利率，我们的无风险利率是在相同时期的银行一年期的存款利率。

三、回归方法与过程

本文通过对变量的选取与计算得出个股收益率、市场收益率，继而通过Eviews6.0计量软件，运用普通最小二乘法进行回归。本文建立了个股收益率Rit对市场收益率Rmt的回归方程： Rit=βRmt+εit对回归结果的分析如下：β值是对股票系统风险大小的度量；R2值是对系统风险在总风险中所占的比例的度量。

以生意宝为例，在Eviews计量软件中运用普通最小二乘法进行回归分析，

四、检验结果与分析

通过对20家电子商务上市公司进行回归分析

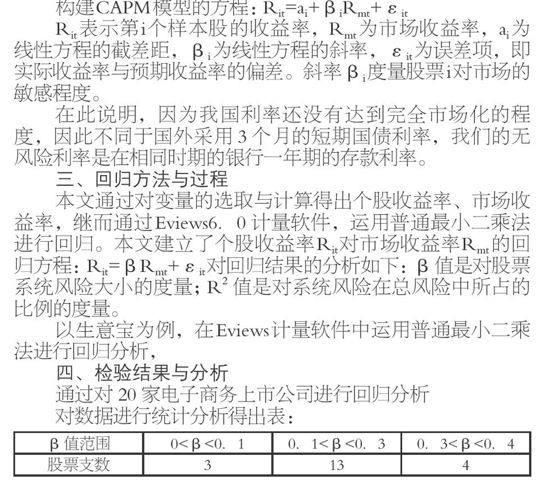
对数据进行统计分析得出表：

β值范围 0<β<0.1 0.1<β<0.3 0.3<β<0.4

股票支数 3 13 4

通过对表回归结果中β值大小的分析，得出20家样本上市公司股票的系统风险均比平均风险小。β平均值为0.194432061，说明电子商务上市公司个股走势与大盘走势基本一致，但是，样本公司个股的β平均值较小，说明其系统风险较低。分析表中的R2值，回归结果中20 家样本公司的R2值均小于0.5，R2平均值为0.17353685，这说明样本股的系统风险在总风险中所占的比例偏低，平均比例约为 17.354%。从R2 值区间分布情况来分析， R2主要分布在 （ 0.1-0.3） 的区间上，没有超过 0. 5 的股票，进一步证实了电子商务上市公司的系统风险较小。综上可分析得出电子商务上市公司的风险主要由公司基本面的非系统风险组成。

五、结论

通过运用Eviews6.0计量软件进行回归及根据相关CAPM理论进行回归结果分析，我们得到以下结论：（1） 电子商务上市公司的系统风险较低。对于风险厌恶型投资者可以选择投资该类型公司个股，在低风险下获取适量收益。（2）电子商务上市公司的系统风险占总风险的比例偏低，电子商务上市公司的风险主要由公司基本面的非系统风险组成。这表明，在投资该行业时，投资者不仅要关注系统风险，更要加强对此类公司基本面的非系统风险分析。

参考文献：

[1]农小玲.广西上市公司系统风险分析[A].市场论坛 2012.（09）：63-64

[2]张晓峒，Eviews使用指南与案例[M]，机械工业出版社，2007.2：55-63

[3]李子奈.潘文卿.计量经济学[M].高等教育出版社.2005.4：22-52

[4]张宗新.投资学.复旦大学出版社.2013.12：76-103