基于事件触发网络控制系统的分布式控制

吴文，刘斌，姚靖，韩贝贝

（湖南工业大学电气与信息工程学院，湖南株洲412007）

基于事件触发网络控制系统的分布式控制

吴文，刘斌，姚靖，韩贝贝

（湖南工业大学电气与信息工程学院，湖南株洲412007）

针对网络带宽有限造成的网络中传输信息量受限问题，引入分布式事件触发机制，即子系统只在它的局部状态误差超过了某个给定的阈值时才传输它的状态信息到它邻近的子系统，研究了网络控制系统基于事件触发机制的分布式控制策略的实现问题。首先，设计了事件触发机制，以保证整个网络系统的渐进稳定性；然后，将所得到的结果运用到线性时不变系统上；最后，通过模型仿真验证了所得到的结论。通过事件触发机制可以减少网络中的信息传输量，降低网络负载，从而提高网络传输效率。

事件触发；分布式控制；网络控制系统

0 引言

随着科技的不断进步，网络技术飞速发展，使得其在各行各业都得到了广泛的应用。在控制领域中，控制系统越来越趋向于网络化、智能化、分布化，网络控制系统（networked control systems，NCS）成为了目前网络技术研究的一大热点[1-7]。

在电力网络、交通网络等网络控制系统中，分布着众多的子系统，称为控制节点（或代理），各节点通过公共网络耦合连接，节点信息由网络来进行传输与交换，所以研究网络控制系统的关键在于考虑各子系统之间信息的联系[8]。然而，网络的带宽是有限的，如何更高效地利用有限的网络带宽来传输更多的信息将会是一个很有意义的课题。此外，网络上的信息传输可能会出现传输延迟的问题，以及信息在网络上传输也可能会丢失，即数据丢包的问题等，都是值得研究的课题。

传统的系统控制中，一般采用周期触发机制，即周期地触发控制任务。当系统处于良好性能运行时仍然周期地触发控制任务就会浪费通信资源。因此，为了避免资源浪费，引入事件触发机制，让控制任务按需执行，以降低控制信号的更新频率，提高动态网络的传输效率[9]。另外，集中式的控制算法需要所有子系统的状态信息，这就要求有一个强大的通信网络及时传输这些状态信息，且需要各子系统间联系的确切模型。这些都限制了集中式控制的规模[10]，因此，对于一个大的网络控制系统，用集中式方式进行控制不切实际。而分布式控制中，子系统可以利用自己及邻近子系统的状态来触发控制任务，这表明可以利用空间上相邻子系统的局部联系来有效调节分布式系统的性能。

为此，本文提出了一种事件触发机制的分布式控制方式，利用事件触发机制以达到降低子系统的通信频率并且降低网络带宽要求的目的。在该方式下，只有当子系统的局部状态误差超过给定的阈值时才传输它的状态信息到邻近的子系统。首先，对网络控制系统进行建模，通过建模引入问题；然后，利用Lyapunov分析法分析网络控制系统基于事件触发的分布式控制的渐进稳定性，并针对线性子系统进行局部事件的分布式设计，以确保整个系统的渐进稳定性；最后，通过仿真实验对所得结论的有效性进行了验证。

1 问题陈述

考虑一个动态网络有N个子系统，这N个子系统相互耦合，且相互从邻近的子系统中接收信息。令N={1, 2, …, n}，N为子系统的数量。子系统用i表示，i∈N。

1.1 模型建立

对于一个包含N个线性时不变子系统的网络控制系统，选定一个子系统i作为研究对象。不考虑外在扰动，则子系统i的状态方程可以写作：

Ni是子系统i的邻近子系统集合，若子系统j是子系统i的邻近子系统，即j∈Ni，则子系统i也必是子系统j的邻近子系统，即i∈Nj。

子系统i的控制输入可以由以下方程产生：

假设信息传输均不存在延迟，本文提出一个分布式事件触发机制来确定每个子系统的Ki和Di，以保证整个系统的渐进稳定性。

2 局部事件设计

本部分讨论如何利用事件触发来保证整个系统的渐进稳定性。定义

利用V作为建立事件触发机制的一个条件。可得如下引理1。

引理1对于式（1）所示的系统，当

1）系统的控制输入是式（2）中的分布式控制，且由式（6）中定义的测量状态作为状态反馈；

2）Pi，Ki，Qi都满足式（3）；

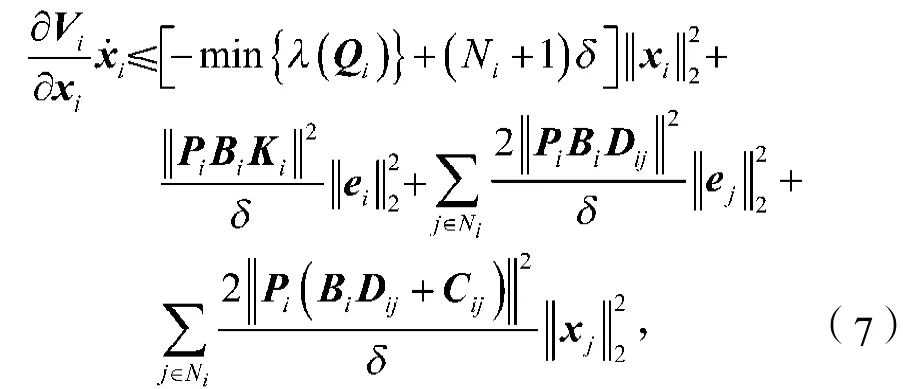
根据对式（7）中Vi求导的计算，可以证明以下定理1能确保整个系统的渐进稳定性。

定理1假设对于所有的i和j满足BiDij=-Ci，在引理1的假设情况下，对于所有的i∈N，若以下不等式成立，则在控制输入为式（2）时，系统（1）是渐进稳定的。

由于所谓“邻近”的关系是对称的，即j∈Ni，则i∈Nj。因此，可以重新分配式（18）中第二行的后半部分来组成含有的部分，则可以得到

定理1得证。

从定理1中可以看出，式（14）中的误差条件只取决于子系统i能直接测量到的量。也就是说，如果所有的子系统能够以传输它们的状态这个意义上配合的话，则式（14）中的阈值条件是一直满足的，那么，就保证了整个系统的渐进稳定性。

如此一来，可以利用式（14）中的不等式来建立状态传输的事件触发机制。注意到不等式在子系统i的传输时刻是平凡满足的。那么，如果触发下一个传输，在式（14）被违反之前，或者说，如果在系统的所有子系统上都能保证这个性能，则这个网络控制系统是渐进稳定的。

定理1中假定的匹配条件有很大的局限性，下面的定理2将放宽这个局限性。

定理2假定引理1中的假设是成立的，假如对于所有的j∈Ni，i∈N有

那么，控制输入为式（2），在满足式（22）的前提下，式（1）所示网络控制系统是渐进稳定的。

证明由于式（21）中Wi的定义，可以保证式（23）不等号右边为正。因此，式（23）成立就意味着式（24）成立。现在考虑候选的Lyapunov函数，由引理1可以把V的方向导数写作

由于“邻近”是相互的，可以把式（25）中的第二行后半部分和第三行重新配置，得到

因此，式（27）不等号右边是负定的，这就意味着，系统在平衡点处是渐进稳定的。

定理2放宽了定理1的匹配条件，则可以得到，存在对称矩阵Pi, Qi和Ki, Dij，分别满足式（3）和式（21），即有

基于此，首先可以假定Pi和Qi都是固定的，然后利用式（28）来决定控制增益Ki和解耦矩阵Dij。另一种方案是首先选择合适的Ki，使得解耦的系统满足给定的鲁棒稳定性，然后利用式（28）来决定Pi和Dij。采用这种方案可以得知，Vi对于网络控制系统是一个鲁棒稳定的Lyapunov函数。

3 仿真实例

考虑一个网络控制系统，它含有3个节点，每个节点的状态都是一维的，如下：

式（29）中：

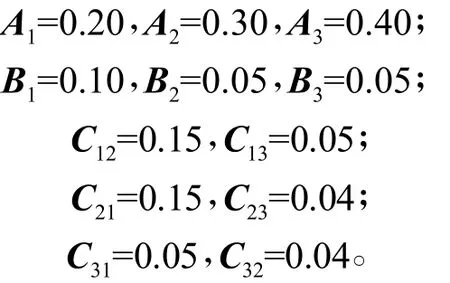
系统控制输入为

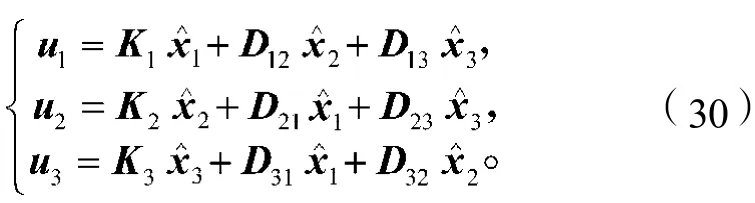
式（30）中：K1=3.0，K2=4.0，K3=2.0。

由条件BiDij=-Cij，可得

给定系统初始状态为[-1.300 81.027 95.735 2]，在没有事件触发控制的情况下，设定仿真时间为6 s，图1即为系统在没有事件触发控制时的节点状态仿真曲线。

图1 没有事件触发控制的节点状态曲线Fig.1Node state curve without event-triggered control

由图1可以看出，系统状态曲线是发散的，说明此系统是一个不稳定的系统。

由前文得出的结论，建立给定系统的事件触发控制机制。

给定系统初始状态为[-1.300 81.027 95.735 2]，设定仿真时间为6 s，得到在事件触发控制下，3个节点的状态仿真曲线如图2所示。

图2 有事件触发控制的节点状态曲线Fig.2Node state curve with event-triggered control

由图2可以看出，系统的状态曲线收敛到0，表明系统在事件触发机制下由不稳定变为稳定。

4 结语

本文研究了基于事件触发的网络控制系统的分布式控制，利用Lyapunov稳定性理论，证明了系统在事件触发控制下的渐进稳定性，并且设计了系统的触发事件。最后通过具体的仿真实验验证了结论的正确性。

本研究只是基于事件触发机制的网络控制系统分布式控制的初步研究。在今后的工作中，还有很多重要问题函待解决，主要有：

1）本文所研究的网络控制系统是线性时不变系统，如果将研究对象扩展到非线性系统，可以推断，得到的结论应该也是相似的，而匹配条件将会再次成为分析的主要问题。

2）本研究未涉及信息冲突问题，但是在实际系统运行中，信息冲突会延迟信息的传送，进而影响系统的稳定性。对于信息冲突给整体系统的稳定性造成影响的情况，文献[8]中提出的边界延迟有助于对其进行分析。

3）文中的理论基于利用解耦匹配条件来进行控制器综合，利用定理2的条件来设计网络控制系统的解耦增益及Lyapunov函数，今后的研究中，分布式控制器的综合问题将是该方面研究的主题。

[1]Wang Xiaofeng，Lemmon M D. State Based Self-Triggered Feedback Control Systems with L2 Stability[C]//17th IFAC World Congress. Seoul Korea：[s. n.]，2008：15238-15243.

[2]Yu H，Antsaklis P J. Event-Triggered Output FeedbackControl for Networked Control Systems Using Passivity: Triggering Condition and Limitations[C]//2011 50th IEEE Conference on Decision and Control and European Control Conference (CDC-ECC). Orlando：[s. n.]，2011：199-204.

[3]Postoyan R，Tabuada P，Nesic D，et al. Event-Triggered and Self-Triggered Stabilization of Distributed Networked Control Systems[C]//2011 50th IEEE Conference on Decision and Control and European Control Conference (CDC-ECC). Orlando：[s. n.]，2011：2565-2570.

[4]Dimarogonas D V，Frazzoli E. Distributed Event-Triggered Control Strategies for Multi-Agent Systems[C]//47th Annual Allerton Conference. Allerton House，UIUC，Illinois：[s. n.]，2009：906-910.

[5]Donkers M C F，Heemels W P M H. Output-Based Event-Triggered Control with Guaranteed L∞-Gain and Improved Event- Triggering[C]//Decision and Control (CDC)，2010 49th IEEE Conference. Atlanta：[s. n.]，2010：3246-3251.

[6]Wang Xiaofeng， Lemmon M D. Self-Triggered Feedback Control Systems with Finite-Gain L2 Stability[J]. IEEE Transactions on Automatic Control，2009，54(3)：452-467.

[7]Yue Dong，Tian Engang，Han Qinglong. A Delay System Method to Design of Event-Triggered Control of Networked Control Systems[C]//2011 50th IEEE Conference on Decision and Control and European Control Conference (CDC-ECC). Orlando：[s. n.]，2011：1668-1673.

[8]廖晓昕. 稳定性的理论方法和应用[M]. 武汉：华中科技大学出版社，2010：18-20. Liao Xiaoxin. Stability Theory and Application[M]. Wuhan：Huazhong University of Science and Technology Press，2010：18-20.

[9]胡松林. 基于事件触发机制的网络化控制系统的分析与综合[D]. 武汉：华中科技大学，2012. Hu Songlin. Analysis and Synthesis of Networked Control Systems with Event-Triggering Scheme[D]. Wuhan：Huazhong University of Science and Technology，2012.

[10]Wang Xiaofeng，Lemmon M D. Event-Triggering in Distributed Networked Control Systems[J]. IEEE Transactions on Automatic Control， 2011，56(3)：586-601.

（责任编辑：廖友媛）

Event-Triggered Based Distributed Control in Networked Control Systems

Wu Wen，Liu Bin，Yao Jing，Han Beibei
（School of Electrical and Information Engineering，Hunan University of Technology，Zhuzhou Hunan 412007，China )

Aiming at the problem of limited transmitting information capacity resulted by restricted network bandwidth, introduces the distributed event-triggered mechanism, which a subsystem broadcasts its state information to its neighbors only when the subsystem local state error exceeds a given threshold. Studies the implementation of event-triggered distributed control strategy for networked control systems. First designs event-triggered scheme to guarantee the entire system asymptotic stability; then applies the obtained result to linear time-invariant systems; finally verifies the conclusions through the model simulation. The event-triggered mechanism reduces the amount of transmission information and the network load, and it improves the network transmission efficiency.

event trigger；distributed control；networked control systems

TP202+.1

A

1673-9833(2014)04-0061-06

10.3969/j.issn.1673-9833.2014.04.014

2014-04-25

吴文（1990-），男，湖北孝感人，湖南工业大学硕士生，主要研究方向为混合系统稳定分析及其应用，E-mail：879914190@qq.com