加速追踪设计的方法和应用

唐文清　张敏强　黄宪　张嘉志　王旭

摘要：加速追踪设计（ALD）是一种选择相邻多个群组同时进行短期追踪研究，获得在测量上有重叠的多个群组追踪数据，对多个群组数据进行合并建构一条在时间跨度上较长的发展趋势或增长曲线的方法。ALD结合真追踪和横断设计的特征，既保持真追踪设计的大部分优点，克服真追踪研究中由于重测效应和被试缺失导致的问题，又尝试分离年龄、群组和历史时间效应，在发展心理研究有重要应用。已有研究探讨ALD的数据分析方法、ALD的有效性及设计特征。未来研究应关注拓展设计条件下ALD的适应性，探索非线性假设或群组效应显著时的数据分析方法和ALD中缺失数据处理问题。

关键词：追踪研究：加速追踪设计；数据分析方法；设计特征

分类号：B841

1、问题提出

心理学研究中常采用横断设计和追踪设计方法研究心理与行为发展变化过程及影响因素。横断设计（cross，sectional design，CSD）同时收集不同年龄群组（cohort）被试的数据，通过比较不同群组的差异，鉴别个体心理发展的某些方面是否与年龄有关。横断研究可快速得到研究结果，有较高时效性，但面临群组效应（cohort effect，也叫朋辈效应）与年龄效应（aging effect）的混淆，不能真正提供关于个体发展过程的信息，通过横断研究描述个体的心理发展过程有很大局限（Bell，1953；Hofer，Thorvaldsson，&Piccinin，2012；Stanger&Verhulst，1995）。

追踪设计是在一段时间内对研究对象进行多次测量，描述心理与行为发展变化的方法。广义的追踪设计（10ngitudinal design）包含多种类型，但“真正的追踪研究”是指“预期的追踪研究”（刘红云，张雷，2005），也叫固定样本追踪设计或真追踪设计（trile longitudinal design，TLD）（Moerbeek，2011）。TLD在一段时间内对同一组被试的心理特质进行反复观测，获得长时追踪数据，相比CSD，TLD可直接研究心理与行为的变化过程，分析个体随时间变化在发展水平、变化速度的差异，鉴别导致不同结果的影响因素（Bell，1953；Duncan&Duncan，2012；Hofer et al.，2012），在发展心理研究中有越来越广泛应用。但TLD要求长时间对一组被试进行追踪研究，经济消耗大，面临严重的被试缺失、重测效应及研究结果过时等问题，影响研究结果的有效性。TLD只对一组被试进行追踪研究，难以确定心理与行为的变化是由自身发展成熟引起，还是由不同测量时间下的历史、文化因素引起，即年龄和历史时间效应（period effect）的混淆（Duncan&Duncan，2012；Duncan，Duncan，&Hops，1996；Duncan，Duncan，&Strycker，2006a）。TLD在实际应用中也常受到被试和时间等研究条件的限制而不能顺利实施（Bell，1953，1954）。

由于CSD和TLD在发展心理研究应用的局限，在很长一段时间内，研究者都在寻找一种既可保持CSD和TLD的优点，又可减少CSD和TLD局限的方法。针对此问题，Bell（1953）最早提出结合了CSD和TLD特点的收敛设计（convergence design），认为同时对多个横断群组进行追踪研究，连接多个群组数据获得近似TLD的研究结果，可很大程度克服CSD和TLD在发展心理研究应用的局限，并在研究中初步证实通过收敛设计获得近似TLD结果的有效性。加速追踪设计（accelerated longitudinal design，ALD）是在收敛设计思想的基础上发展起来。

文章将在阐述ALD的概念及优点的基础上，重点阐述ALD的数据分析方法、ALD的方法研究和应用现状，讨论ALD方法及相关研究存在的问题，提出进一步的研究方向。

2、ALD方法的概述

收敛设计思想提出后，许多研究者对这种方法的特征、有效性及应用作了充分论述（Nesselroade&BaRes，1979；Schaie，1965），并在数据分析方法研究方面取得重要成果，促进了这种研究设计的发展（Duncan et al.，1996；Duncan，Duncan，&Hops，1 994；Raudenbush&Chan，1992，1993）。为体现收敛设计对CSD和TLD特点的结合，并与TLD相区别，把这种方法称作加速追踪设计（ALD）（Tonry，Ohlin，&Farrington，1991；Duncan et al.，1996），或群组序列设计（cohort-sequential design）（Nesselroade&Baltes，1979；Schaie，1965），也叫混合纵向设计（mixedlongitudinal design）（Berger，1986；Jang，2011），把TLD称作真追踪研究（true longitudinal study）（Duncan et al.，1996）或纯追踪研究（purelongitudinal study）（Jang，2011）。综上所述，ALD是选择相邻多个群组同时进行短期的追踪研究，获得在测量上有重叠的多个群组追踪数据，对多个数据的连接和合并建构一条时间跨度较长的发展趋势或增长曲线的方法。

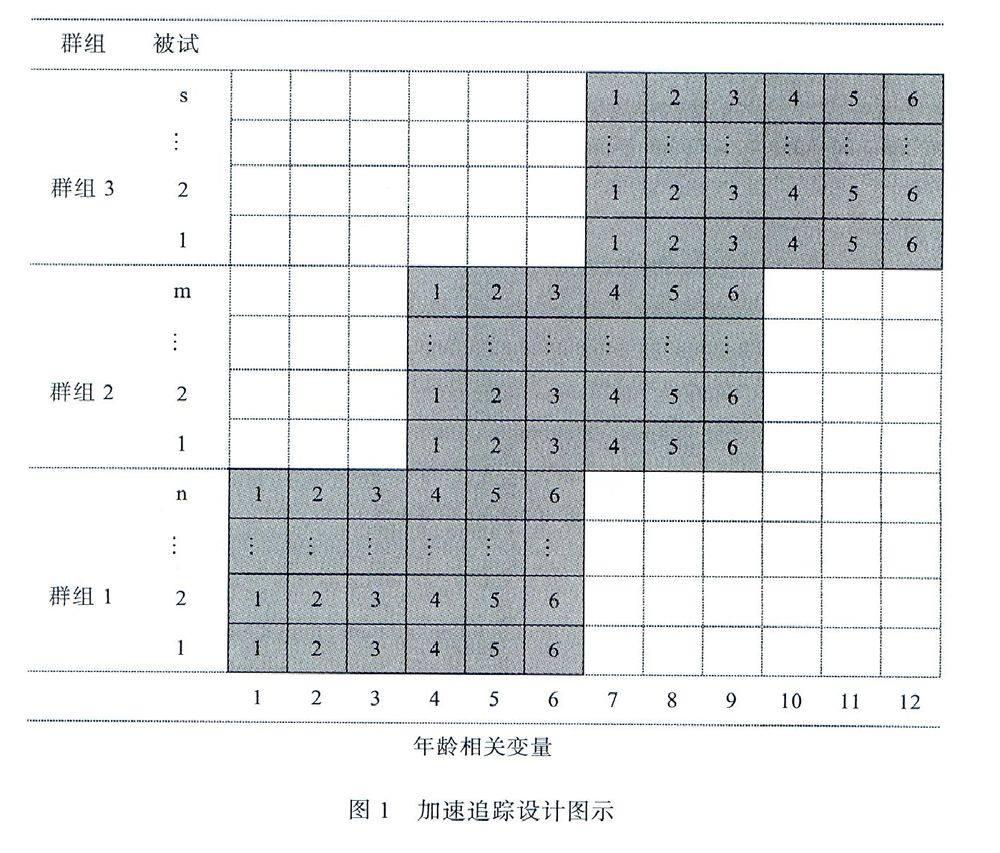
ALD同时纳入群组变量、年龄相关变量、测量次数和测量重叠度变量，有3个重要特征（如图1是一个对3个年龄群组同时进行6次测量，测量重叠为3次的ALD研究）。首先，ALD纳入一个横向的群组变量作为较高级的分组变量，群组间依次相邻，每个群组包含一定样本量被试，群组间样本量可不同，同一时间测量可获得横断数据（见图1中群组和被试栏）。第二，纳入纵向的年龄相关变量（如年龄、年级）和测量次数变量（如图1中横轴表示年龄，每行的实线单元格数表示测量次数，方格中的数据表示测量时间点，虚线单元格表示该群组被试未被测量的时间点），对多个群组同时追踪研究，可获得多个群组追踪数据。第三，纳入测量重叠度变量，相邻群组的相同年龄在测量上有一定程度重叠（图l中，群组1的第4、5、6次測量与群组2的第l、2、3次测量重叠，即被试年龄相同），使不同群组追踪数据可连接。ALD结合横断研究（选择多个年龄群组）和纵向研究（每个群组都进行追踪研究）的特点，具有单独实施CSD和TLD研究所无法比拟的优点。

首先，与TLD相比，ALD对多个群组同时进行追踪研究显著缩短数据收集持续时间，较快获得研究结果，提高研究的时效性和有效性。TLD选取单一样本进行长时追踪研究，面临选择特殊群体的危险，容易导致严重的被试缺失和研究结果不具时代性，导致无效的研究结果（Watt，2008）。而ALD同时对多个群组进行追踪研究，通过较短的时间追踪就可获得较长时问跨度的追踪数据（如图1中，6次测量的ALD研究可获得12次测量的追踪数据），显著缩短时间，减少经济支出和被试缺失，保证研究过程的组织和控制（Baer&Schmitz，2000；Duncan et al.，1 996；Raudenbush&Chan，1993），降低学习、疲劳、测量材料解释变化等重测效应（Hertzog&Nesselroade，2003）。当要进行长时间追踪研究时（如10年），运用ALD具有更好的时效性和有效性。

其次，ALD在发展心理研究中可相对独立地分析群组效应、年龄效应和历史时间效应，部分解决了CSD和TLD研究中的效应混淆问题。发展心理研究中，基于CSD的研究混淆了年龄效应和群组效应，基于TLD的研究混淆了年龄效应和历史时间效应（Duncan&Duncan，2012；Schaie，1986），要从研究中推论关于个体发展的有效结论，必须对三种效应进行分离。ALD同时纳入群组、年龄、测量时间和测量重叠度变量，研究过程既可分析横向特征和纵向发展，也可比较不同群组的相同年龄被试的差异来评估群组效应，通过横向比较和纵向比较确定年龄效应，从而相对独立地评估年龄效应、群组效应和历史时间效应，得出关于个体发展的有效结论（Baltes，Baltes，&Reinert，1970；Baltes&Nesselroade，1970，1972）。

最后，ALD同时选择多个年龄群组进行短期追踪研究，可获得更多的关于各年龄群组的心理与行为的发展信息，提高研究结果的一般信度（Hertzog&Nesselroade，2003），在大型发展心理研究中尤其重要。

3、加速追踪数据分析方法

ALD优点之一是克服TLD的局限，通过ALD研究获得近似TLD的结果。对ALD的数据进行TLD推论的前提是不同群组的数据是收敛的（convergent），即不同群组的相同年龄被试的发展具有相同的水平和相似形态，用一条共同的线型就可表达多个群组的发展过程。因此，对加速追踪数据分析时要检验群组间追踪数据是否收敛（Anderson，1993，1995；Duncan et al.，1996；Miyazaki&Raudenbush，2000；Tildesley&Andrews，2008）。Bell（1953，1954）通过分析重叠测量年龄组的均值和变化的速度差异来检验加速追踪数据是否收敛，运用方差分析对加速追踪数据进行分析。回归分析也被用于分析加速追踪数据（Harezlak，Ryan，Giedd，&Lange，2005；Tang&Orwin，20091，但未考虑到加速追踪数据的特征。统计方法的发展使基于结构方程的潜变量增长曲线模型（latent growth curve model，LGM）（Duncan，Duncan，&Strycker，2006b；McArdle&Anderson，1990；McArdle&Hamagami，1992）和阶层线性模型（hierarchical linear model，HLM）（Bryk&Raudenbush，1992；Miyazaki&Raudenbush，2000）用于分析加速追踪数据，在检验群组数据收敛性的同时分析发展过程的整体水平和个体差异。

3.1 LGM对加速追踪数据的分析

LGM结合多变量方差分析和结构方程的特点，用类似验证性因素分析的方法定义潜变量，用时间函数确定因子载荷，通过两个潜变量来描述增长趋势和变化特征（刘红云，张雷，2005；Baer&Schmitz，2000；McArdle&Anderson，1990）。其中，截距因子是测量时间WO时，因变量的取值，截距的均值和方差分别描述个体在t=0时的整体均值及个体差异；斜率因子表示个体的变化速度，斜率的均值和方差分别描述整体变化速度和个体差异。基本模型的数学表达式：

y_ti=β_oi+β_IiT_ti+ε_ti（1）

t为重复测量次数，t=1，2，3……T；i=1，2，3……n，y_ti表示第i个被试第t个时间点的测量结果，β_oi、β_Ii分别表示截距和斜率，T_ti为时间变量相关的函数，ε_ti为误差。

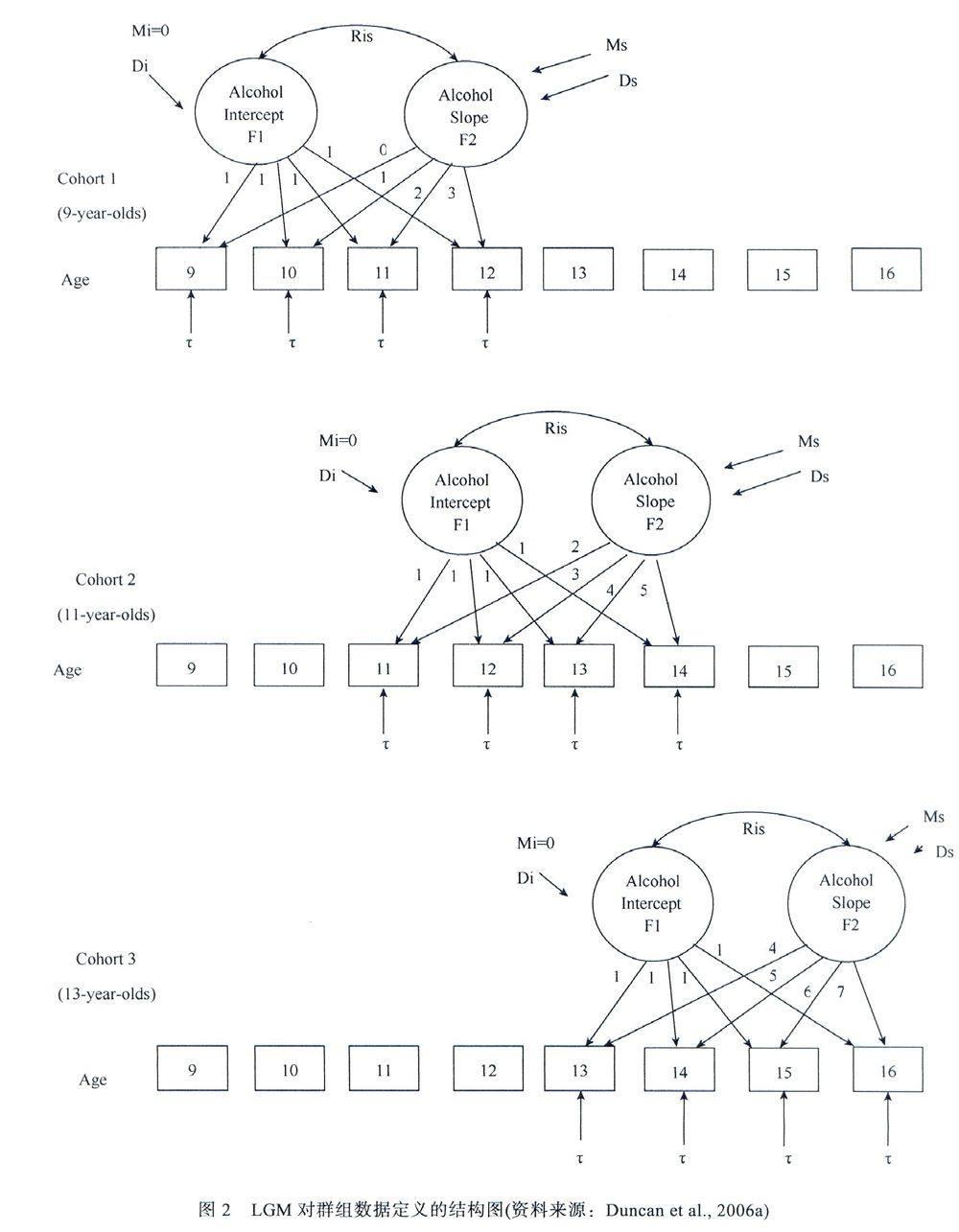
McArdle和Anderson（1 990）较早运用LGM分析加速追踪数据，Anderson，Baer和Duncan等通过一系列研究证实LGM分析加速追踪数据的适宜性（Anderson，1993，1995；Baer&Schmitz，2000；Duncan et al.，1994，1996，2006b）。LGM对加速追踪数据的分析是对不同群组分别定义增长模型，通过限定不同群组发展趋势相同来解决群组间发展是否存在差异及个体随时间的发展趋势问题。如Duncan等（2006a）运用LGM对9、11、13岁群组的青少年酒精使用的加速追踪数据进行分析，研究9-16岁青少年酒精使用的发展特征（见图2）。图2中截距因子载荷限定为1，不同群组的相同年龄在斜率因子的时间载荷定义为相等，限定不同群组发展趋势相同，并随年龄呈线性增长。数学表达式：

Y（t，n=M_i（n）+L（t）M_s（n）+E（t，n） （2）

其中Y（t，n）表示第n个被试第t个时间点的测量值；M_i（n）是截距，M_s（n）是斜率，E（t，n）為误差，L（t）是把变量Y与时间T联系起来的数学函数，若假设变化为线性函数，则每个群组在四个时间点的测量值表达式分别为（以第一、第二群组为例）：

第一群组：

y（1）=M_i+0M_s+E（t）

y（2）=M_i+1M_s+E（t）

y（3）=M_i+2M_s+E（t）

y（4）=M_i+3M_s+E（t）

第二群组：

y（2）=M_i+1M_s+E（t）

y（3）=M_i+2M_s+E（t）

y（4）=M_i+3M_s+E（t）

y（5）=M_i+4M_s+E（t）……

上述模型只简单定义了线性增长模型，在实际研究中，可不固定斜率因子的载荷，运用不定义LGM对数据进行拟合，估计各时间点观测变量对斜率因子的载荷，描述发展趋势（如Duncanet al.，1996）。

根据已有研究（Anderson，1993；Baer&Schmitz，2000；Duncan&Duncan，20 12；Duncan etal.，1994，1996，2006a，2006b；刘红云，张雷，2005），LGM分析加速追踪数据时（以定义LGM为例），首先对不同群组分别建立和定义模型，限定不同群组发展趋势相同来验证数据的收敛性；释放限制模型中的某些限制条件（如群组条件），采用拉格朗日乘数（1agrange multipliers，LM）检验释放限制条件是否可显著提高模型的拟合度（Duncan et al.，2006b）；根据模型拟合度及LM检验值选择模型；最后考察斜率、截距及其均值和方差，分析发展趋势及个体差异等特点。

LGM运用潜变量描述和解释发展趋势和变化的个体差异，通过建模定义和探讨变量之间的关系，在模型上具有很大的灵活性，广泛应用于加速追踪研究的数据分析（De Haan，Prinzie，&Dekovi6，2010；Duncan，Duncan，StryckeL&Chaumeton，2007；King，Molina，&Chassin，2009；Kofler et al.，2011）。但LGM分析加速追踪数据的适应性是基于平衡设计的假设，若ALD在研究应用中的测量间隔或测量次数不等，或研究中要考验时间变化变量（time-vary variable）对发展的影响时，LGM不适用（Duncan&Duncan，1995；Miyazaki&Raudenbush，2000）。

3.2 HLM对加速追踪数据的分析

HLM把追踪数据看成具有嵌套结构的数据，即重复测量嵌套于个体，个体嵌套于群体。HLM可同时分析个体发展趋势和变化的个体差异，直接处理测量间隔或测量次数不等的追踪数据，灵活处理追踪数据中的缺失问题，适用于分析加速追踪数据。当加速追踪研究中纳入时间变化变量，HLM比LGM可更好地分析发展变化的问题（Miyazaki&Raudenbush，2000；Raudenbush，Brennan，&Barnett，1995）。Raudenbush和Chan（1992）首先运用HLM分析加速追踪数据；Miyazaki和Raudenbush（2000）详细阐述了HLM分析加速追踪数据的原理和过程；Watt（2004，2008）及Gerstorf，Ram，Hoppmann，Willis和Schaie（2011）在加速追踪研究中采用HLM分析数据。Moerbeek（2011）系统探讨HLM框架下加速追踪研究的统计功效问题，进一步证实HLM分析加速追踪数据的适宜性。

根据相关研究fMiyazaki&Raudenbush，2000；Moerbeek，2011；Raudenbush&Chan，1992，1993：Watt，2004，2008），HLM分析加速追踪数据的基本假设是简化模型（不纳人群组效应）嵌套于全模型（纳入群组效应）。以2HLM下极大似然（maximumlikelihood）方法为例说明具体步骤。首先，建立全模型并估计参数，其中第二水平包含群组变量（见公式3-5）。第二步，建立简化模型并估计参数（见公式6-8）。第三步，建构似然比检验（likelihoodratio test，LR检验），通过比较两个模型拟合差异统计量选择模型，判断数据是否收敛（LR检验：S=D₁-D₀，D₁为全模型的拟合差异统计量，D₀为简化模型的拟合差异统计量）。其中S服从自由度为单独施于简化模型的限制参数个数的卡方分布（n为大样本），若S大于临界值，拒绝原假设关于简化模型可较好表达加速追踪数据的特征，反之，接受原假设，加速追踪数据收敛，可用一条共同的线型表述多个群组的发展趋势。

全模型：

第一水平：y_ti=π_0i+π_1iT_ti+ε_ti（3）

第二水平：π_0i=β₀₀+β₀₁z_i+μ_0i（4）

π_1i=β₁₀+β₁₁z_i+μ_1i（5）

其中z_i为群组效应的变量。

簡化模型：

第一水平：y_ti=π_0i+π_1iT_ti+ε_ti（6）