视错觉之波动与盲点

如果一条直线与物体表面呈某种角度，并且物体遮住了直线的中间部分，即直线只有两端分别出现在物体的两侧，此时，多数人会感到这条直线发生了“错位”。这种现象是由德国生理学家波根多夫发现的，被称作“波根多夫错觉”。小读者可以画一条至少30厘米长、与水平呈45度角的直线来证明这一点。如果将书横放在线上，使直线两端伸出书的两边，线就显得不连续。

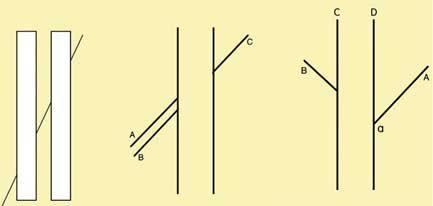
下面三张图都是波根多夫错觉的例子。

被矩形分隔开的斜线似乎是三条独立的直线。事实上，沿直线放一直尺可以证明这三条线只不过是一条直线的三段。

画上第二条线A，与第一条线B平行。多数人会认为线C是与线A相连续的线，其实B与C才是属于同一条线。

线A与线B被线C、线D隔开时，从平面上看，多数人会认为线B将与线A相交于线A与线D的交点a上方的某一点。事实上，线A与线B的交点也是a点。当将杂志向顺时针方向转动约45度并略前倾时，很容易看出来。

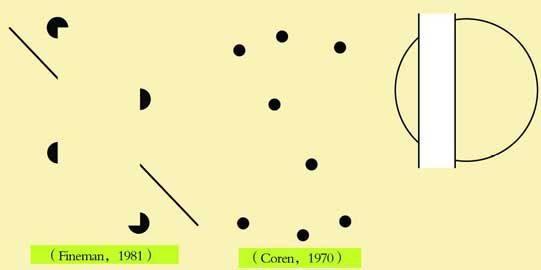
如左图，即使当错位图形是某种错觉轮廓时，仍然会产生波根多夫错觉。

如左图，多数人会认为图中自左上方到右下方的四个点不在一条直线上。

环状的东西似乎是被一对平行线隔开，这使得组成圆环的弧线显得不相连续，看上去左边的弧线所在的圆似乎比右边的弧线所在的圆稍小一点儿。

想击中水里的鱼，你必须调整目标以弥补因光的折射现象造成的误差，鱼并不在你透过水所看到的那个地方。

右图是个最典型的视觉波动的例子。如果能让这张图变大，效果会更加明显。