《财务管理》教学中使用插值法求解的思考

●焦丽

《财务管理》教学中使用插值法求解的思考

●焦丽

插值法是《财务管理》课程教学中对于求解不同时间点上资金之间的换算的一种重要方法，它利用了数学上相似三角形对应边长成比例的原理，巧妙地将数学应用于解决实际问题。但目前一些教材不分情况地对所有时间价值的问题都采用“插值法”解决，是一种教学的浪费。文章先分析插值法的数学原理与固有误差，再对《财务管理》中是否适合使用插值法解决的问题进行分类，最后列举部分问题不使用插值法而使用公式算术法解决的优势。

插值法 财务管理 适用条件

在《财务管理》课程中，围绕时间价值原理对不同时间点上资金之间的换算一直是课程教学中的重点，也是《财务管理》的研究基础。在教学中，借鉴了数学上插值的思想，利用查表得到的几组变量（通常是两组），结合其他给定条件，来求解未知变量，被称为“插值法”。插值法利用了数学上相似三角形对应边长成比例的原理，巧妙地将数学应用于解决实际问题。但目前一些教材和教学中，不分情况地对所有时间价值的问题统统采用“插值法”解决，是一种教学的浪费，使得一些本来不必大动干戈的题目小题大做。因而在何种情况下使用“插值法”是由题目的条件和求解变量的特点来决定的，在不必使用“插值法”的情况下，使用算术法更有优势。

一、插值法的几何意义及固有误差

在数学界，插入法最早是在1976年由两位运筹学家提出，最初是为求解车辆路线问题所提出的解决方法。《财务管理》应用中使用的“插值法”是指简单的线性插值法，其几何意义是相似三角形对应边长成比例的原理。下面举一例来说明简单线性插值法的几何意义。

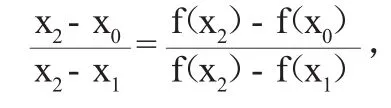
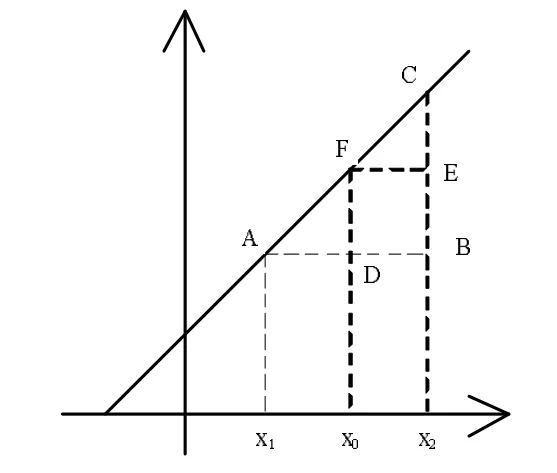
图1

假如，这条曲线不是直线，这个求得的值就不是一个准确值，这是使用插值法的一个问题。往往在《财务管理》中研究的图像都不是线性的，故使用插值法求得的结果与真实结果之间必然有一个误差存在。假如图1中的曲线画的稍微弯曲一些，便可以得到图2。在图2中，我们可以清楚地看到使用插值法求得的结果与真实结果之间的误差△x0，所以在使用插值法解题之前，往往会有一个关于可接受的误差范围的假设，在这一假设前提下，可以将这个误差忽略不计。但是，对于部分货币的时间价值问题，从精确和经济的角度来思考，完全可以不采用插值法，得到一个比插值法更精确的结果，而且也不比插值法复杂。要做到这一点，就要先对所求解的问题做一个分类。

图2

二、按未知量在时间价值系数中出现次数对所求问题的分类

分类之前，为方便下文分析，先明确两个概念：公式算术式和公式算术法。所谓公式算术式，是指在《财务管理》中一般常见的货币时间价值问题，按照货币时间价值原理列出的，含有求解的未知变量的方程式。比如，已知现值P，终值F，折现率i，求期数n，可以得到的公式算术式F=P（1+i）n。公式算术法，是指通过公式算数式来求解未知量的方法。仔细观察《财务管理》中最常见的时间价值系数，我们可以发现。对于像求解复利终值系数、复利现值系数中的折现率i或者期数n的这类问题，所得到的公式算术式中折现率i或者期数n只出现一次或者容易变形公式算术式得到一个不含未知量的式子，通过一般的数学计算器可以得到一个精确结果。可对于像求解年金终值系数、年金现值系数中的折现率i或者期数n的这类问题，所得到的公式算术式中折现率i或者期数n不只出现一次或者不容易变形公式算术式得到一个不含未知量的式子，通过一般的数学计算器往往也不容易得到一个精确结果。所以，按照上述的分类方法，可将求解复利终值系数、复利现值系数中的折现率i或者期数n的这类问题分为一类。将年金终值系数、年金现值系数中的折现率i或者期数n的这类问题分为第二类。在《财务管理》教学中，对于第一类问题应该使用简单明晰的公式算术法来解决，第二类用公式算术法解决起来较为麻烦的问题，采用“插值法”更合适。

三、正确分类使用“差值法”的优点

通过长期的实践教学与关注大量的《财务管理》教材后，发现在很多书籍中凡遇到诸如前述四类基本货币时间价值理论相关的计算时，都不分情况地对所有的问题统统采用“插值法”解决。这种作法即是一种浪费，使得一些题目小题大做，又不利于学生正确理解时间价值的原意。因此，在实践教学中，应该按照以上所述的分类方法对求解变量仅在公式算术式中出现一次的题目不使用插入法而使用简单的公式算术法，对求解变量在公式算术式中多次出现的题目使用插值法。这样做的好处有以下三点。

1.使学生更好地理解插值法在财务管理学习中的意义。在财务管理的学习中引入插入法，只是一个工具的作用，目的是为了解决财务管理中货币的时间价值问题。部分教材在不分具体条件的情况下，对所有的货币时间价值问题都采用插值法解决，会让学生陷入一种误区之中，学生会以为学习的重心是使用插入法解题。其实不然，教师应该将财务管理中货币时间价值的原理推到教学的中心，将理解货币时间价值作为教学的重点，而不单单是告诉学生们只要用插入法就可以解决所有问题。对于学生将来的学习工作都会造成不良后果，可能会让很多人忽略掉问题的本质——货币的时间价值，或者会让他们缺少对于插值法之外的其他方法的思考。因此，在教学中，对问题适当地进行分类，将会有利于学生更好地理解插值法在财务管理学习中的意义。

2.明晰考点，避免非必要的查表得数。这一优势紧承上一个优势。在考试中，如果过分强调使用插值法解题，考试的重心就成了考插值法，而偏离了原来的中心——考察对货币时间价值的理解。在考试中，对于适合使用公式算术法去解决的问题，应该让学生使用公式算术法来解答。这样避免了不必要的查表得数，因为这个问题本身是不需要使用插值法这样的较为“高端”的方法。而且这样做还能避免学生产生一种误区，查表得数是需要的时候自己查得的，而不是在任何时候都会给定的。这样将会更有利于学生理解插值法在财务管理学习中的意义。由此，前两个优势是相互联系的。

3.结果更精确。在求解复利终值系数、复利现值系数中的折现率i或者期数n的这类问题中使用公式算术法，相比较使用插值法最直接的优势是结果更精确。现举例说明。

假设，已知现值P=84，终值F=100，期数n=4，求折现率i（保留三位有效数字）。另外，在n=4时，复利现值系数PVIF=0.855，i=4%，复利现值系数PVIF=0.823，i=5%。

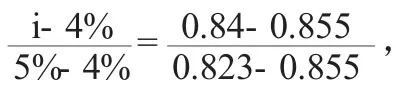
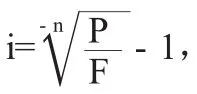
四、结论

插值法是《财务管理》课程教学中对于求解不同时间点上资金之间的换算的一种重要方法。在教学中使用时应该对所求问题分类后再决定是否使用。对于像求解复利终值系数、复利现值系数中的折现率i或者期数n的这类问题，所得到的公式算术式中折现率i或者期数n只出现一次或者容易变形公式算术式得到一个不含未知量的式子，使用公式算术法解决更加精确合理；对于像求解年金终值系数、年金现值系数中的折现率i或者期数n的这类问题，所得到的公式算术式中折现率i或者期数n不只出现一次或者不容易变形公式算术式得到一个不含未知量的式子，则适宜使用插值法。

[1] 吕红.简易插值法在财务管理实务中的应用[J].大众商务，2009（1）

[2] 刘高常，谢林海.利用斜率原理解析财务管理中的插值法[J].商场现代化，2009（2）

[3] 田笑丰.财务管理教学中插值法的快速理解和掌握[J].会计之友，2008（4）

（作者单位：太原理工大学阳泉学院管理工程系 山西阳泉 045000）

（责编：芝荣）

G642

A

1004-4914（2014）01-264-02