永磁同步电机位置伺服系统滑模控制的研究

孙路路 王玲丽

(安徽工程大学 电气工程学院，安徽 芜湖241000)

0 引言

工业对象的多样化和复杂化对伺服控制器提出了更高要求，即希望伺服系统具有一定的自适应能力和较强的抗扰能力，滑模变结构控制（SMC）能较好地解决这个问题[1]。SMC是50年代俄罗斯学者提出的一种有效的非线性鲁棒控制方法[2]。由于它不需要对系统的精确观测，控制率整定方法简单，易于数字实现，近年来，已有学者将SMC应用于伺服系统中，研究表明，它能有效改善摩擦非线性和负载时变性，提高系统鲁棒性[3-4]。

本文根据矢量控制PMSM伺服系统的特点，设计了一种SMC控制器，通过对控制量先微分后积分的处理，使其不含非线性项，减小了抖振；通过对伺服系统采取先速度SMC后位置SMC的方式，实现了位置跟踪和速度控制。文中将该方法应用于矢量控制PMSM伺服系统，仿真和实验结果均表明所设计的SMC控制器能使实际系统较好地实现位置跟踪和速度控制，较大地提高系统的快速性和鲁棒性，并减小抖振，有效地改善电机的动静态特性。

1 永磁同步电机数学模型

假设磁路不饱和，在空间磁场呈正弦分布，不计磁滞和涡流损耗影响条件下，采用id=0的PMSM转子磁场定向控制，转矩的大小只与定子电流的幅值成正比，实现了PMSM的解耦控制。这时，PMSM电压方程：

式中：ud、uq分别为 d、q 轴电压；id、iq分别为 d、q 轴电流；Ld、Lq分别为 d、q轴电感；r为定子电阻；Te为电磁转矩；P为电机的极对数；Ψa为永磁体与定子交链的磁链；TL为负载转矩；J为转动惯量；ω为转子机械角速度。

2 控制器的设计

伺服系统采用图1所示的控制方案，用SMC代替传统P与PI的双环控制。

SMC是基于相平面的控制，如图2示。其基本思想是将任一点出发的状态轨迹通过控制作用引导到滑模面（阶段a），同时保证系统在滑模面上的运动是渐近稳定的，即为滑动模态（阶段b）。

图1 伺服系统框图Fig.1 The structure of servo control system

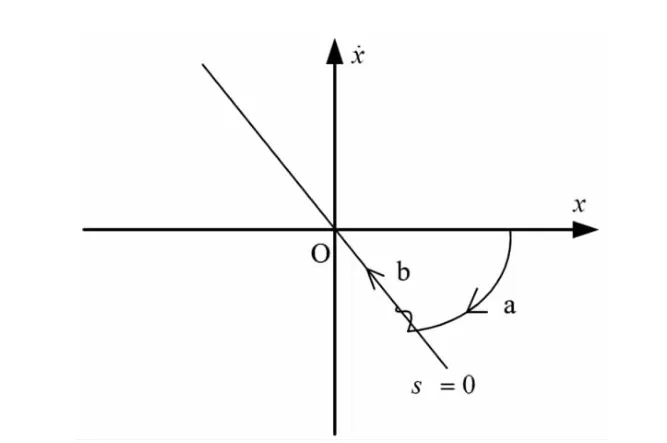
图2 SMC系统相平面轨迹Fig.2 The phase trace of SMC system

对系统位置采取SMC控制，取系统状态变量：

设计切换函数：

则由SMC到达条件 ss˙＜0得：

图4是在给定角度200°时，采用位置SMC的仿真波形。可见，系统最终能无超调地达到稳定。

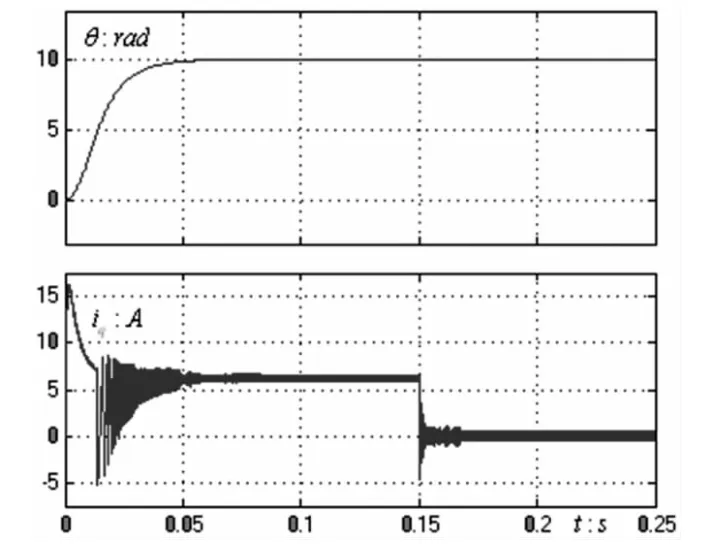
图3 突卸负载iq和位置误差波形

图4 伺服系统位置和速度波形

3 结论

本文针对矢量控制的PMSM伺服系统的特点，设计了一种SMC控制器，仿真表明，所设计的SMC控制器能有效实现PMSM速度和位置伺服。

［1］Kuo-Kai Shyu，Chiu-Keng Lai，Yao-Wen Tsai,，and Ding-I Yang.A Newly Robust Controller Design for the Position Control of Permanent-Magnet Synchronous Motor[J].IEEE Transaction on Industrial Electronics，2002，49（3）：558-565.

［2］葛宝明，郑琼林，蒋静坪，于学海.基于离散时间趋近率控制与内模控制的永磁同步电动机传动系统[J].中国电机工程学报，2004，24（11）：106-111.

［3］张希，陈宗祥，潘俊民，王杰.永磁直线同步电机的固定边界层滑模控制[J].中国电机工程学报，2006，26（22）：115-121.

［4］刘云峰，缪栋.电液伺服系统的自适应模糊滑模控制研究[J].中国电机工程学报，2006，26（14）：140-144.