基于ADS的集总参数带通滤波器的优化设计

杨 柱,朱倩倩,艾治余,王 攀,赵小平

（西安石油大学,西安 710065）

基于ADS的集总参数带通滤波器的优化设计

杨 柱,朱倩倩,艾治余,王 攀,赵小平

（西安石油大学,西安 710065）

滤波器在通信系统中应用较为广泛，利用滤波器的选频作用，可以滤除通信中的干扰噪声或测试中进行频谱分析。本文利用ADS软件设计一款带通滤波器，并对其进行优化和瞬态仿真分析。经过分析得出，在满足其他各项设计指标要求的前提下，优化后的滤波器选频特性得到明显提高。

带通滤波器；ADS；优化仿真；瞬时仿真

1引言

在现代通信系统中，滤波器的应用领域很广泛，如电视频道信号的选取，多音响装置的频谱分析器等，滤波器作为无线通信应用领域的一个重要器件，其性能指标往往直接影响到整个通信系统的优劣，伴随着移动通信、雷达、卫星通信等各通信系统的增多，电磁环境逐渐异常复杂化，从而使得通信系统中频带资源愈发短缺，导致频率间隔变得越发密集。怎样无失真的从逐渐短缺的频带资源内获取所需的信号并抑制其他无用或有害的信号，为滤波器的设计提出了苛刻的要求。虽然各滤波器在电子器件和技术的飞速发展的推动下层出不穷，但怎样制造小体积低成本易加工量产并满足指标要求的滤波器渐渐成为工程应用中的核心问题，集总参数滤波器以其自身优势作为首选应用在通信系统和设备中。

集总参数是指当实际电路的尺寸远小于电路工作时电磁波的波长时，可以把元件的作用集总在一起，用一个或有限个理想R、L、C元件来加以描述的电路参数。集总参数带通滤波器是指由集总参数元件构建的滤波器，其特性由构建此带通滤波器的集总参数元件值来确定。本文阐述了利用ADS（Advanced Design System）软件设计带通滤波器的方法、流程以及仿真过程，结合带通滤波器的一般原理和最小二乘误差法，以期寻找一种更为通用的、频带高度利用和相邻信道低干扰的带通滤波器的设计方案，同时给出其仿真结果。

2 工作原理

带通滤波器[5]是指能通过某一频率范围内的频率分量、但将其他范围的频率分量衰减到极低水平的滤波器。一个理想的带通滤波器应该有一个完全平坦的通带，在通带内没有放大或者衰减，并且在通带之外所有频率都被完全衰减掉，另外，通带外的转换在极小的频率范围完成。

理想带通滤波器实际是不存在的。滤波器并不能够将期望频率范围外的所有频率完全滤除，因为滤波器存在滚降现象。通常，滤波器的设计尽量保证滚降范围越窄越好，这样滤波器的性能就与设计更加接近。然而，随着滚降范围越来越小，通带就变得不再平坦，开始出现“波纹”。这种在通带的边缘处尤其明显的效应称为吉布斯现象。

在频带较低的剪切频率f1和较高的剪切频率f2之间是共振频率，这里滤波器的增益最大，滤波器的带宽就是f2和f1之间的差值。如图1所示：

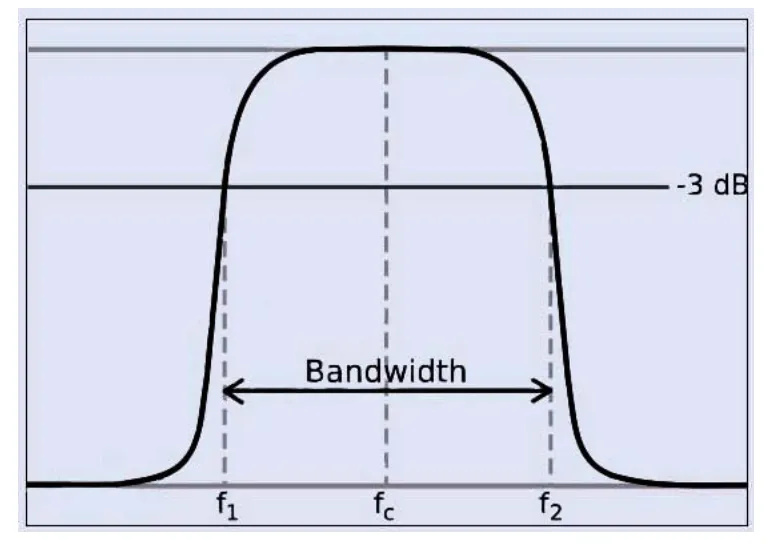
图1 带通滤波器的选频特性

3 带通滤波器的设计指标

3.1 滤波器中心频率为80MHz

3.2 通带频率范围为76MHz～84MHz

3.3 通带内最大衰减为3dB

3.4 在65、95MHz时衰减大于30dB

3.5 特性阻抗选为50欧

4 带通滤波器的仿真设计与优化

4.1 带通滤波器的仿真设计

4.1.1 依据上面所给的技术指标值利用ADS软件提供的滤波器设计向导创建的集总参数带通滤波器原理图[2][4]如下图2所示

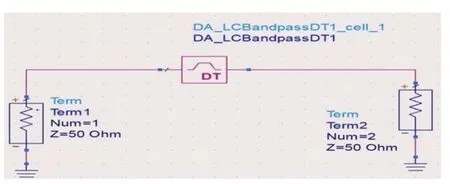
图2 带通滤波器原理图

4.1.2 经过S参数仿真后的仿真结果图如下图3所示

仿真点名称m1 m2 m3 m4 m5 m6 Freq（MHz）95.00 65.00 90.00 70.00 84.00 76.00 dB（S（2,1））-43.256 -49.439 -30.158 -33.841 -3.000 -3.000

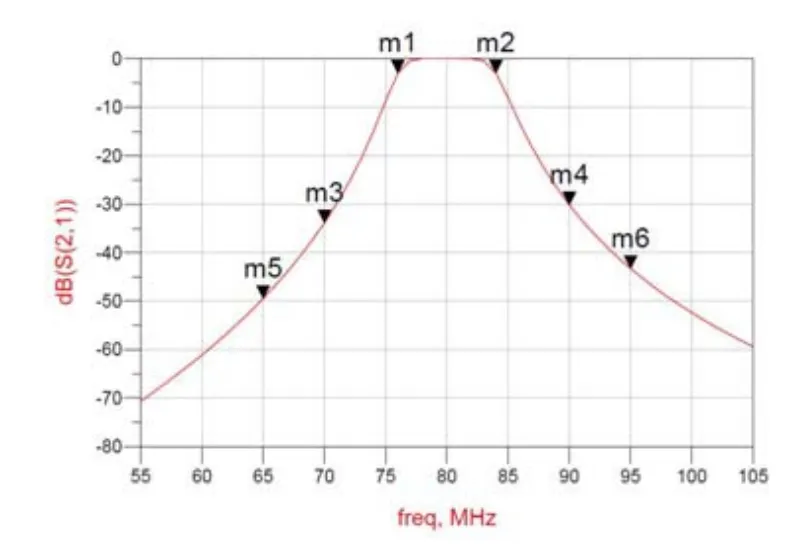
图3

4.2 实际的集总参数带通滤波器

集总参数元件之间需要有传输线连接，由于分布参数的影响，传输线会对滤波器的技术指标有影响，因此需要考虑加入传输线后滤波器的设计情况。其设计指标在原基础上附加如下三项板材指标：

（1）微带线基板的厚度选为1mm,基板的相对介电常数选为4.2

（2）连接集总参数元件的微带线，长选为4mm,宽选为1.5mm

（3）连接集总参数元件的弧形微带线，半径选为2.5mm,宽选为1.5mm

由此构建的带通滤波器的原理图[3]如下图4所示：

图4 带通滤波器的原理图

其相对应的S参数仿真结果如下图所示图5所示：

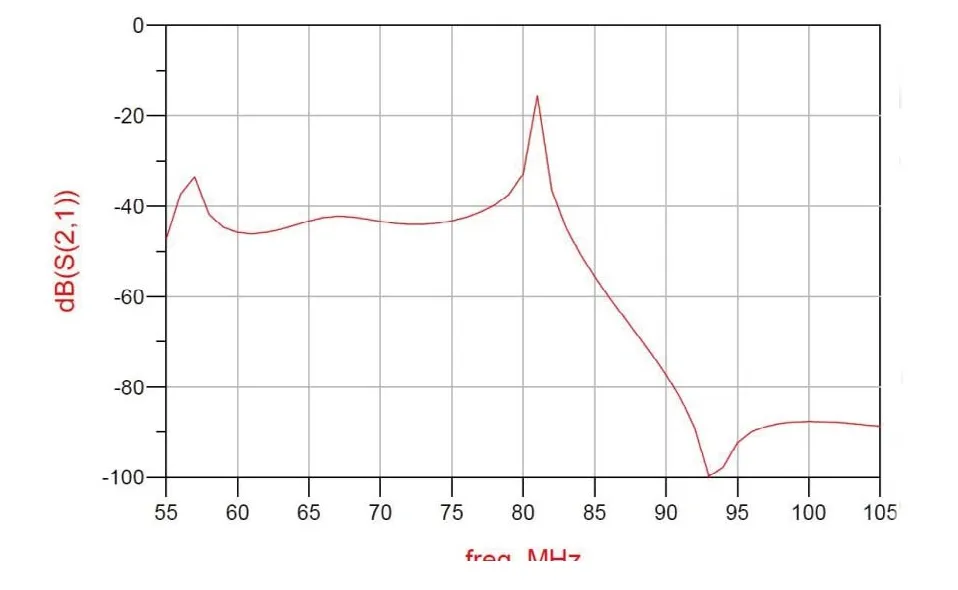
图5 S 参数仿真结果

由上图可知，不符合指标要求，需对其电路进行优化处理。

本文对该滤波器电路的优化是建立在所给传输线的指标值不变的前提下对各集总参数元件的优化，即合理选取集总参数元件L1、L2、L3、L4、C1、C2、C3和C4的值，来获取满足技术指标的带通滤波器设计方案。

4.3 优化设计

4.3.1 优化理论

ADS提供了多种优化器，本文使用随机优化器最小二乘误差函数（最小二乘EF）法来进行优化。

随机优化器使用随机搜索方法在一个随机数量范围内借助随机数发生器获取一个参数值，从已知的一组初始的参数值的误差函数开始微扰每个初始值，来重新评估误差函数，借助最小二乘误差函数确保找到至少一个当时最低结果且有一定的概率来找到全局加权最小值。

最小二乘EF形式：EF=∑Wi*|simulationi-goali|2[1]

其中，Wi表示加权系数；simulationi表示仿真值；goali表示目标值。用最小二乘误差函数的计算方法是为每个指定的目标在每个频率/功率点个别评估误差，随后算得该误差平方幅值在频率和/或功率的平均。

其误差贡献eij（f）形式如下：

eij（f）=（|Rij（f）-gij|/di）2

其中，di表示第i个目标正常化的因子，其值由参数设置的最小最大值决定；Rij（f）表示第i个目标值下正被优化的第j个频率范围的响应；gij表示第i个目标值第j个频率范围对应的优化准则Rij（f）响应。di的取值情况如下：

（1）di=（|Min|）0.5如果只在第i个目标组件指定最小值。

（2）di=（|Max|）0.5如果只在第i个目标组件指定最大值。

（3）di= {（|Min|）0.5+（|Max|）0.5}/2 如果在第i个目标组件同时指定最大值和最小值。

（4）di=1.0 如果指定的最大值与最小值经上面的方程计算的值是零。

其在第j个范围内超过设定频率的总误差响应形式如下：

Eij=Wij*∑（f∈Fj）eij（f）

Wij表示第i个目标值第j个频率范围对应下的权重因子；Fj表示指定的第j个频率范围内的频率值。

其误差函数在i范围内求和并除以Nj,求得第j个范围内的误差贡献如下

Ej=∑i[Wij*∑eij（f）]/∑i∑Nij（f）

其中，Nj表示在Fj的频率范围内的频率的数量。

在整个j范围内求得的误差贡献如下：

E=∑Ej

总的误差贡献表达式如下：

E=∑j{∑f[∑iWij*eij（f）]}/Nj}

依据以上公式计算各参数值来使得E最小，从而达到设计的最优。

4.3.2 经过优化控件优化多重优化后得到以下相应的优化参数如下：

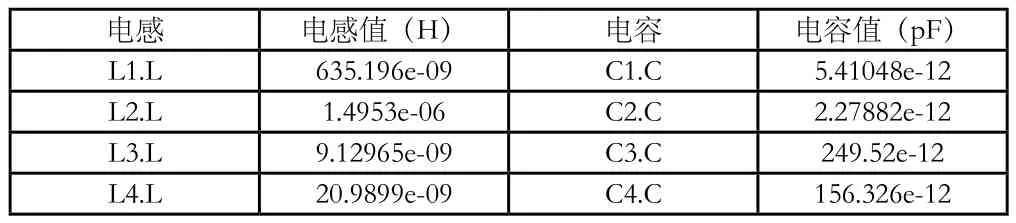
电感 电感值（H）电容 电容值（pF）L1.L 635.196e-09 C1.C 5.41048e-12 L2.L 1.4953e-06 C2.C 2.27882e-12 L3.L 9.12965e-09 C3.C 249.52e-12 L4.L 20.9899e-09 C4.C 156.326e-12

即：经过优化之后，相应的电容、电感值对应如下：

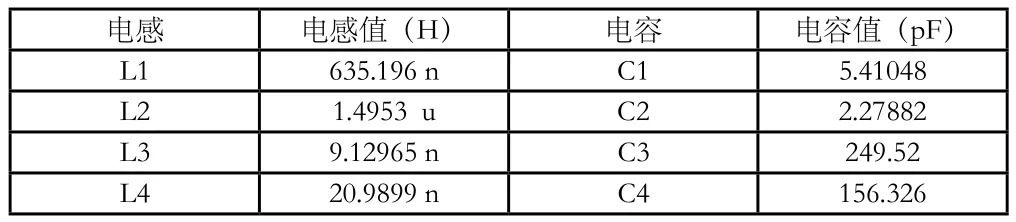
电感 电感值（H）电容 电容值（pF）L1 635.196 n C1 5.41048 L2 1.4953 u C2 2.27882 L3 9.12965 n C3 249.52 L4 20.9899 n C4 156.326

4.3.3 经过多重优化后其对应的整体仿真结果如下图所示图6所示：

仿真点名称 m1 m2 m3 m4 m5 m6 Freq（MHz）76.00 84.00 60.00 100.00 65.00 95.00 dB（S（2,1））-0.555 -2.422 -48.516 -45.605 -37.497 -35.230

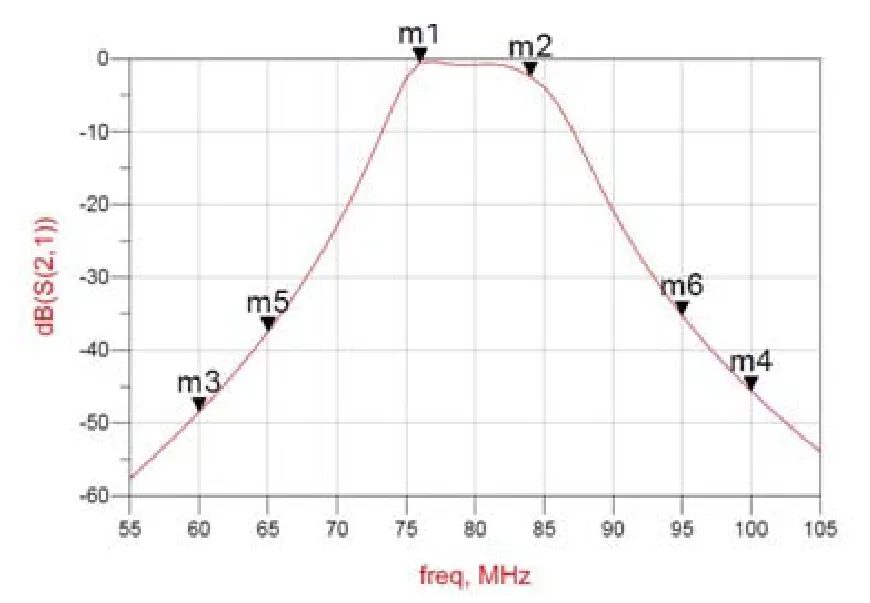
图6 整体仿真结果

由上图可以看出，S（2,1）曲线在60、76、84和100MHz处的值分别为-48.516dB、-0.555dB、-2.422dB、-45.605dB。

以上数据满足带通滤波器的设计技术指标。

5 瞬态仿真分析

（1）对上面的原理图做一下修改，添加瞬态仿真控制器等，并对其参数作修改。修改的参数为StopTime=20/（80e6）；MaxTimeStep=1/（2*20*80e6）；

（2）插入一个Vin和Vout的矩形图，对每条轨迹进行编辑（Trace（Options））,然后Place symbol at data（数据添加符号），这将显示发生在仿真中的时间点。相应的仿真图如下图7所示：

m2 time=190.0nsec Vin=496.6mV

m1 time=190.5nsec Vout=173.4mV

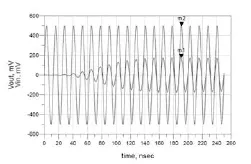
图7 仿真结果图

（3）现写一个方程式来计算通过滤波器的延迟：marker_indifferent.运用indep函数会计算标记之间在X轴上的差（独立变量=time）。相应的结果显示如下图8所示：

经过瞬态仿真控制器的仿真分析，可得知：在放置Marker的地方，所得值有细微的差别，且信号从输入端经过此带通滤波器后到输出端的延迟约为31ps.这是因为信号经过滤波器时需要过去所有的数据来进行一些运算，而这些数据通常是由实际滤波器的相移所决定，即：通过将信号延时一小段时间让它们能够“看到”未来的一小部分来近似地实现理想滤波器；还有就是信号经过滤波器时，信号在滤波器内部的传输线上传输时也会产生延时，一般是信号频率升高时，通过滤波器后，其相位滞后加大。

6 设计总结

带通滤波器在通信系统中有着广泛的应用，Agilent公司的ADS软件在电路设计与仿真方面有着独特的优势。本文利用ADS软件设计集总参数带通滤波器，根据设计要求设计所要制作的滤波器的原理图，并运用ADS软件提供的Random Optimizer对其进行优化和进行Simulation-Transient与Simulation-S_Param仿真分析，其选频特性显著提高。使用ADS软件设计电路不但减轻了设计者的劳动强度，缩短了设计周期，而且提高了设计精度和设计效率，为电路等的开发设计带来了方便。

[1]黄玉兰.ADS射频电路设计基础与典型应用[M].北京人民邮电出版社，2010.

[2]范博.射频电路原理与实用电路设计[M].北京机械工业出版社，2007.

[3]赵建勋，陆曼如，邓军等.射频电路基础[M].西安电子科技大学出版社，2010.

[4]王文祥.微波工程技术[M].国防工业出版社，2009.

[5]钟蔚杰，杨景曙 .微带线带通滤波器的ADS辅助设计[J].现代雷达，2008（03）：83-85.

杨柱（1989-），男，安徽淮北人，硕士研究生，研究方向：通信与信息系统。