Flapping Characteristics of 2DSubmerged Turbulent Jets in Narrow Channels＊

Sun Jianhong（孙建红），Chen Yue（陈悦），Zhou Tao（周涛），Liu Ke（刘可）

College of Aerospace Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing，210016，P.R.China

1 Introduction

The flapping motion of a turbulent plane jet，a lateral oscillation of the jet，were investigated theoretically and experimentally by Goldschmidt and Bradshaw［1］.Sun et al［2］obtained the governing equation of flapping motion through theoretical analyses，and showed an important flow characteristic，i.e.，in the flapping jet there exists a flapping－induced Reynolds stress，which can be utilized to enhance the mixing or dilution of jet flow fields.Therefore，a considerable interest has been held in the design，performance and flow control of diffusers or mixers in chemical engineering，environmental engineering，and so on.Wu et al［3］pointed out the relation between the oscillatory frequency and water depth for a jet slot with a constant width，and it is evident from the research of Hsu et al［4］and Sun［5］that the self－excited jet flapping motion is attributed to the jet instability rather than the coherent turbulent structure.Hsu et al［4］studied the flapping motion of plane jets of different water depths，jet－orifice slot widths and jet exit velocities.Results showed that the critical instability condition of flapping motion is governed by two parameters，that is，the water－depth to jet－slot－width ratio（H－z0）／d and the Strouhal number St＝f0d／W0c（a dimensionless parameter defined by flapping frequency，critical exit velocity and the jet slot width），where z0is the virtual origin of the jet，Hthe water depth，dthe jet slot width，f0the flapping motion frequency and W0cthe critical jet exit velocity.

In recent years，most of research work have focused on the numerical simulation of flapping motion of turbulent submerged plane jets［6－12］.It was clearly presented in Ref.［11］that the flapping phenomenon was verified simultaneously by laser Doppler velocimeter（LDV）measurement and numerical analyses with volume of fluid approach coupled with a large eddy simulation turbulent model.Moreover，the general agreement of mean velocities between numerical and experimental results in self－similar region is good for the flapping jet，and the decay of the mean velocity along the jet centerline is considerably faster than that of the stable impinging state.Zhao et al［10］presented the detail flow field in numerical simulation，and pointed out that the frequency of longitudinal velocity oscillation at the jet centerline was twice of that of the transverse oscillation，and the mean centerline velocity decay was much faster than that of the stable impinging jet without flapping motion.Moreover，the magnitudes of flapping－induced velocities almost had the same order of that of the turbulent fluctuation，which implied that the flapping－induced components are as important as the turbulent fluctuation for flapping jet.

In addition to numerical simulation，Sun et al［13］addressed the wall effect on Darcy′s law by experimental measurement in Hele－Shaw cells.In order to study the effect of wall on the flapping pattern of a submerged turbulent water jet in narrow channels，the flow field was visualized by a laser－induced fluorescence（LIF）system at different Reynolds numbers［14］.Those LIF images showed that the flow motion in a narrow channel differs from the motion of a turbulent plane jet without narrow channels.Three flow patterns are detected in narrow channels，namely，stable impinging，stable jet with recirculation vortices and flapping turbulent jet.

In this paper，the flow field of submerged vertical turbulent jets in narrow channels is measured by a wave height gauge and LDV.Two main motives dominate the work of this paper is to verify whether flapping motion still exist for vertical turbulent jet under the effect of narrow channel，and whether the frequency of flapping will be the same as that of plane jet.

2 Experimental Set－up

The impingement and flapping motion of vertical 2Dturbulent jet were observed with a narrow channel in a rectangular water tank，which is 6mlong，0.4mwide and 0.4mhigh，as shown in Fig.1.The slot of narrow channel，which is also considered as a Hele Shaw（H－S）cell，made up of two glass plates，with the length of 1.8m，the height of 0.4mand the thickness of 5mm.The turbulent jet is governed by ajet generator located in the middle of the tank.The jet generator has a convergent bell－shape orifice of 2mm wide（d＝2mm）and 10mm or 6mm long（b＝10 mm or 6mm）.Actually，for a 2Dturbulent plane jet，the width of narrow channel is regarded as infinite，i.e.b＝ ∞ .With the water depth of H＝100mm，200mm and 260mm，it obtains H／d＝50，100and 130.The water is re－circulated with apump system，to maintain the water level at constant during measurement.At the ends of the tank，two absorbers are used to eliminate the reflection of surface waves.

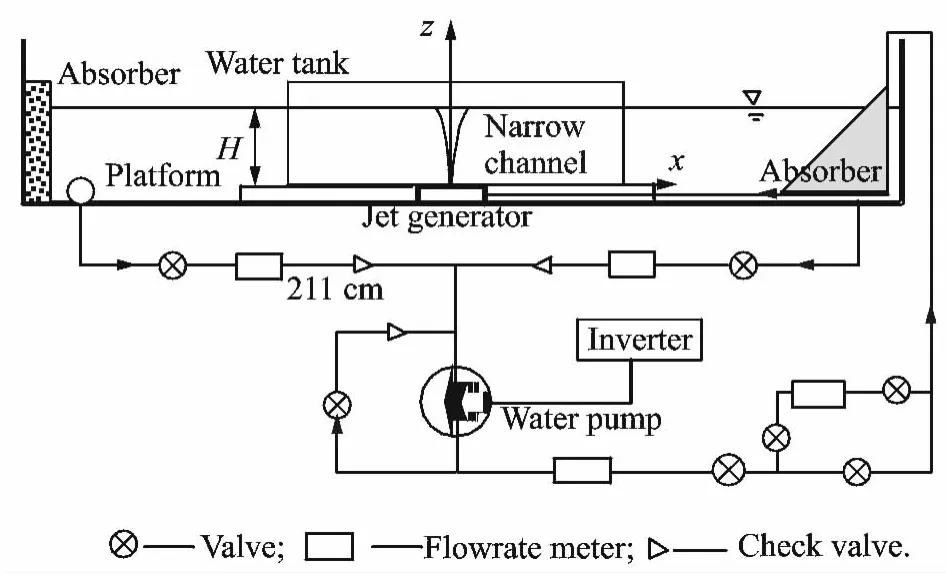
Fig.1 Schematic diagram of experimental set－up

The velocity of turbulent jet is measured by a LDV system mounted on a 3Dtraverse.To increase the data rate of the LDV system，the flow field is seeded with titanium oxide（TiO2）particles of 1—5μm in diameter.To obtain the phase angle of flapping motion，the oscillation of the water surface deformation is measured by a capacitance wave height gauge and used as a reference.The signal of the capacitance gauge is recorded by a TSI IFA300system.

3 Natural Flapping Frequencies

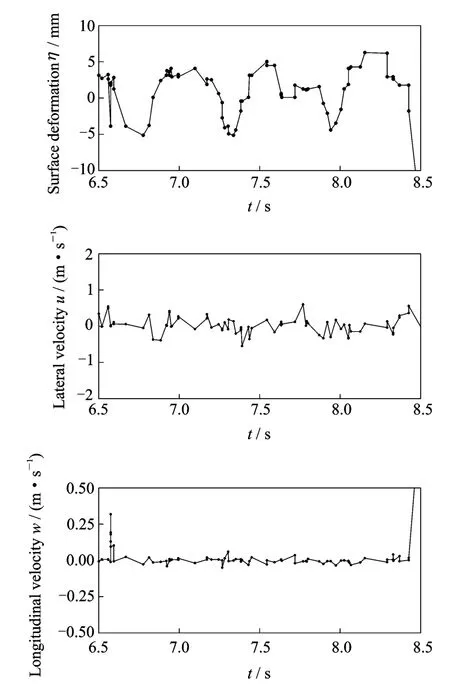
Fig.2 Time variation of the surface displacement and jet centreline velocities measured by LDV located at z／H＝0.56and W0＝5.16m／s

Fig.2shows the signals of surface deformation，which are gathered by the water height gauge，as well as the longitudinal and the lateral velocities obtained by the LDV located at the centreline of turbulent plane jet of z／H＝0.56.The results of power spectrum densities（PSDs），as shown in Fig.3，indicate that there indeed is a low frequency oscillation at the flapping frequency imbedded in the turbulent fluctuations.Figs.3（a）and 3（b）show that the frequency of water surface deformation（SD）is the same as the frequency of lateral velocity measured by LDV at f＝1.66Hz.Since it is the consequence of double passes of jet maximum velocity through the LDV measurement volume for each jet flapping cycle，the frequency of longitudinal velocity oscillation at the jet centreline is twice of the lateral oscillation［5，10］.Unfortunately，the power spectrum densities of longitudinal velocity in Fig.3（c）cannot verify the above results clearly due to the poor random data in Fig.2（c）.However，it is evident that the double frequency phenomenon persists along the jet centreline by theoretical analyses and experimental measurement in turbulent flapping jets.

Fig.3 PSDs of surface deformation，lateral velocity and longitudinal velocity when H＝100mm，z／H＝0.56and W0＝5.16m／s

4 Analyses of Flapping Characteristics in Narrow Channels

Since the water surface cannot keep still with jet impingement and the height of water hump will be increasing with the increase of jet exit velocities，the water hump must be measured firstly in order to analyse the accrual natural flapping frequency in narrow channel.The profile of water hump is shown in Fig.4，when the initial water depth（without jets）is H＝100mm.Obviously，the height of hump will raise with the increase of jet exit velocities W0when W0＜W0c.However，the height will decrease when W0＞W0csince the width of hump becomes large.In this section，the average height of hump when W0approaches to W0cwill be regarded as，so do for the other cases of water depth from 50mm to 220mm.Here，is about 20mm for H＝100mm.

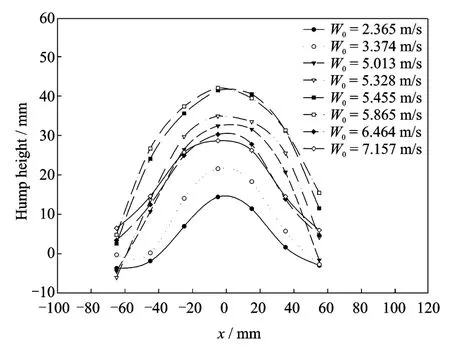
Fig.4 Water surface humps in different jet exit velocities when H＝100mm

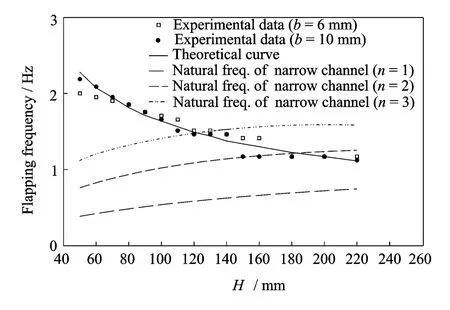
Fig.5 Self－excited flapping frequencies with different effective water depths in narrow channels（b＝6，10mm）

The self－exited flapping motion still exists in narrow channels.Measurement results indicate that the natural flapping frequency is constant for a defined water depth，which does not change with the increase of W0.It is the same as that of turbulent plane jets.Fig.5reflects the relation between flapping frequency f0and effective water depth He.One can tell that the experimental data agree well with the theoretical curve［5］，as rewritten in Eq.（1）.

where gis the gravitational acceleration，He＝H－z0＋the effective water depth.

Meanwhile，the frequencies of two different order steady waves are also illustrated in Fig.6，which gives a clear explanation for those data departed from the theoretical curve.According to the wave theory in shallow water，the disturbance or a wave with small amplitude in H－S cells or narrow channels will be reflected in the two ends of cells，with the behaviour of a series of standing waves.Considering that the jet is mounted on the centre of narrow channels，the wavelength and frequency can be indicated as

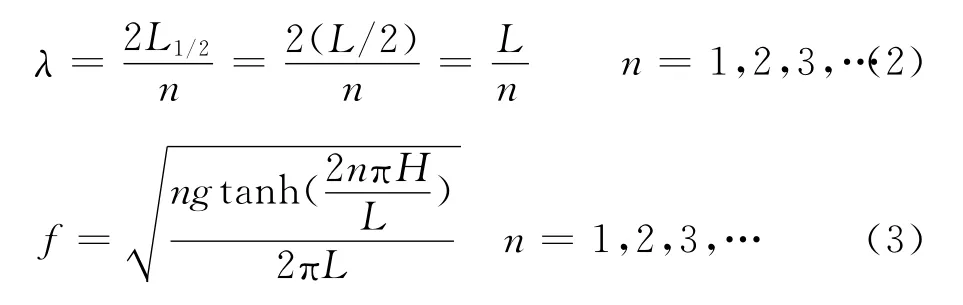
where Lis the length of a narrow channel.The disturbance with defined frequencies will excite the flapping motion as soon as possible when the disturbing frequency is approaching to the natural flapping frequency.From Fig.6，it has no effect on the flapping frequency f0when the disturbance frequency is much less than f0.On the contrary，the effect is also very small when the disturbance frequency is so large that will decay very fast in narrow channels.Therefore，in present experiment，the effect of n＝2is apparent，and the flapping frequency will lock－in the disturbing frequency when the disturbing frequency is near and less than the natural flapping frequency.That is similar to the effect of surface wave on the 2Dturbulent plane jet［15］.

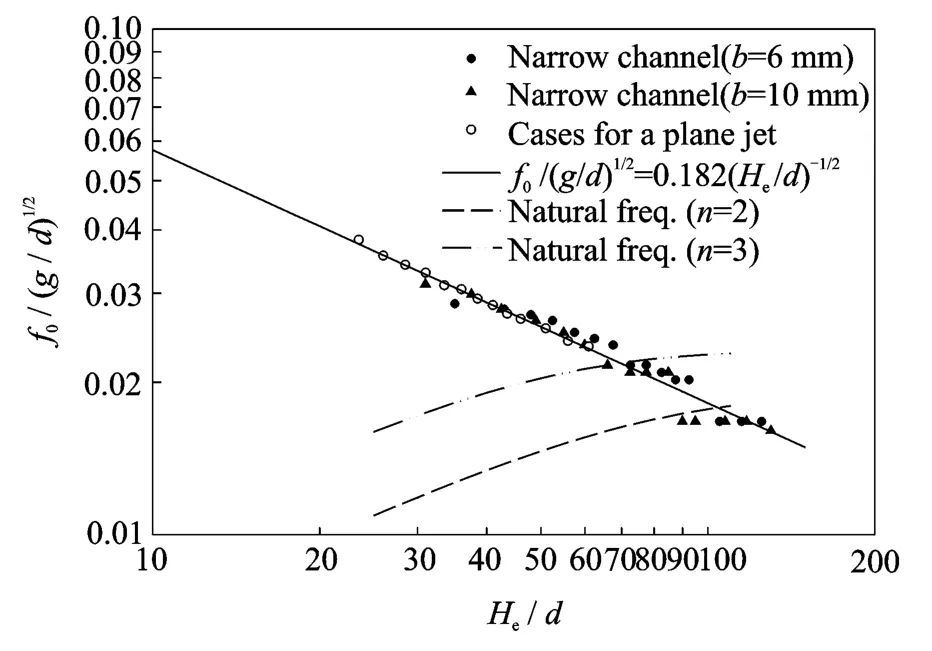
Fig.6 Variation of flapping frequency with different effective water depths and jet orifice widths in H－S cells（b＝6，10mm）

An experience equation is also used to indicate the flapping frequency in narrow channels，as shown in Fig.6.It is obvious that，for these ca－ses with a small effect of reflected surface disturbance wave，the measured frequency at the inception of jet flapping motion for different effective water depths and jet orifice width is presented in terms of f0／and He／dfor a turbulent plane jet，which can be rewritten as

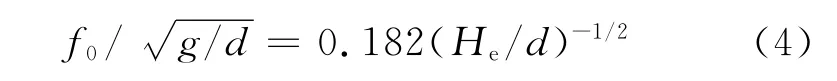
Actually，Eq.（4）takes a form of－1／2power，which is coincident with Eq.（1）.How ever，it does not agree with Eq.（2）under the surface disturbing reflected wave，for instance，He／d＞70and He／d＞90.That indicates the frequency of flapping in narrow channels is the same as that of 2Dturbulent plane jets.

Fig.7presents a curve of critical jet exit velocities in different effective water depths，where the width of narrow channel remains 10mm.The critical velocities in narrow channels will shift more than that of a turbulent plane jet.Although the effect of surface disturbing water waves will make it out of good linearity when He／d＞70，the linearity is good when He／d＜70，which can be expressed by a fitting result

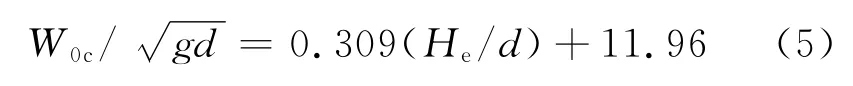
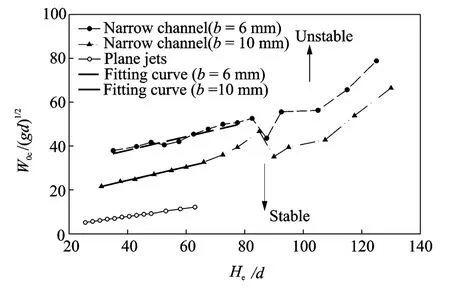
Fig.7 Critical jet exit velocity which onsets jet flapping motion in narrow channels（b＝6，10mm）

Comparing with plane jet，the slope is larger in narrow channels.Therefore，the wall effect can keep the water hump more steady，and increase the critical jet exit velocity.However，under the effect of surface disturbance waves，the instability of water hump increases with the frequency of disturbing wave approaching to the natural flapping frequency.

5 Conclusions

The experimental study is carried out on the self－excited flapping motion of submerged vertical turbulent jet in narrow channels.At a fixed water depth，the turbulent jet in narrow channels is also observed to flap at a nearly constant frequency when the jet exit velocity is greater than a critical velocity，which proves that the flapping motion is a flow pattern of 2Dturbulent jet either for submerged vertical plane jet or in narrow channels，even though the detail of flow field is not exactly same.It is found that the water depth His a most important parameter to the critical jet exit velocity W0cand jet flapping frequency f0.The results indicate that W0cincreases with Hand the jet flapping frequency f0is then found to be inversely proportional to the water depth H.Meanwhile，theoretical analyses on experimental result show that the surface disturbance wave changes the frequency of flapping motion，i.e.the flapping frequency will lock－in the disturbing frequency when the disturbing frequency is near and less than the natural flapping frequency.

［1］ Goldschmidt V W，Bradshaw P.Flapping of a plane jet［J］.Phys Fluids，1973，16：354－355.

［2］ Sun J H，Zhao L Q，Hsu C T.Theoretical analyses on flapping motion of submerged turbulent plane jets［J］.Modern Physics Letters B，2005，19（28／29）：1471－1474.

［3］ Wu S，Rajaratnam N，Katopodis C.Oscillating vertical plane turbulent jet in shallow water［J］.Hydraulic Research，1998，36（2）：229－234.

［4］ Hsu C T，Kuang J，Sun J H.Flapping instability of vertically impinging turbulent plane jets in shallow water［J］.Journal of Engineering Mechanics，2001，127（5）：411－420.

［5］ Sun J H.Flapping turbulent plane jets in shallow water and interacting with surface waves［D］.Hong Kong，China：Hong Kong University of Science and Technology，2001.

［6］ Majanded P，Siikonen T.Large－eddy simulation of a round jet in a cross－flow［J］.Int J Heat Fluid Fl，2006（27）：402－415.

［7］ Zhao L Q，Sun J H.A novel numerical visualization of submerged plane water jets［J］.The 9th Asian Symposium on Visualization.Hong Kong：［s.n.］，2007.

［8］ Espa P，Sibilla S，Gallati M.SPH simulations of a vertical 2－D liquid jet introduced from the bottom of a free surface rectangular tank［J］.Adv Appl Fluid Mech，2008（3）：105－140.

［9］ Zhao L Q，Sun J H，Zhou P P.Numerical simulation on flapping motion of submerged plane water jets［J］.Modern Physics Letters B，2009，23（3）：329－332.

［10］Zhao L Q，Sun J H.Flow characteristics of flapping motion of a plane water jet impinging onto free surface［J］.Advances in Applied Mathematics and Mechanics，2013，5（6）：846－856.

［11］Sun J H，Zhao L Q，Hsu C T.Experimental and numerical study on the flapping motion of submerged turbulent plane jet［J］.Science China：Technological Sciences，2013，56（10）：2391－2397.

［12］Zhao L Q，Sun J H.Frequency characteristics of flapping motion of submerged impinging jet［J］.J of Vibration，Measurement and Diagnosis，2013，33（3）：445－449.

［13］Sun J H，Hsu C T.Experimental study on Darcy′s law in Hele－Shaw cells［J］.Transactions of Nanjing University of Aeronautics and Astronautics，2003，20（2）：134－139.

［14］Sun J H，Hsu C T.Flow visualization of submerged jets in narrow channels［J］.Modern Physics Letters B，2009，23（3）：377－380.

［15］Sun J H，Kuang J，Hsu C T.Frequency lock－in phenomenon of flapping motion with surface water wave［J］.Transactions of Nanjing University of Aeronautics and Astronautics，2002，19（1）：1－6.