Thermoelastic Damping in Auxetic Plate
Bogdan T.Maruszewski,Andrzej Drzewiecki,Roman Starosta
Institute of Applied Mechanics,Poznan University of Technology,Poznan,Poland
1 Introduction
The reciprocal interactions of the elastic and thermal fields in bodies of finite extent have been considered by many researchers[1-4].The definite geometry of a body can be an origin of certain unusual phenomena.One of them is so-called the thermoelastic damping which has nothing to do with eventual viscous features of the body.The result from that phenomenon of energy dissipation(not observed in the pure elastic body)in the case,for instance,of the thermoelastic plate during its vibrations,comes from an additional heat flux normal to the boundaries of the plate.The origin of that flux is the alternate compression and extension of the upper and lower fibres of that body.This way,in the case of the plate the problem is 2D(plate)-3D(additional dimension resulting from it thickness).Zener[5]first pointed out that one of the mechanisms of thermoelastic damping is based on the stress heterogeneities giving rise to fluctuations of temperature.That idea was,among others,developed by Alblas[6-7]and then by Maruszewski[8].Ignaczak and Ostoja-Starzewski[9]have proposed considerations dealing with the thermoelastic damping based on the extended thermodynamical model[10-11].That phenomenon is crucial in microscience,nanoscience and engineering.
In the recent years materials with so-called negative properties have been accurately investigated for their very interesting and unexpected physical features and behavior.Such properties,among others,are characterized by negative Poisson′s ratio[12-18].
The paper deals with the free and forced bending vibrations of a thermoelastic rectangular plate,in which the thermal field is described also by one relaxation time.The particular analysis has been made both for the classic and auxetic materials.
2 Basic Equations
The subject of our considerations is a rectangular thermoelastic plate:0≤x1≤a,0≤x2≤b,.The equations which govern ther-moelastic processes in that plates with the relaxation of the thermal field have the following forms[2,7].
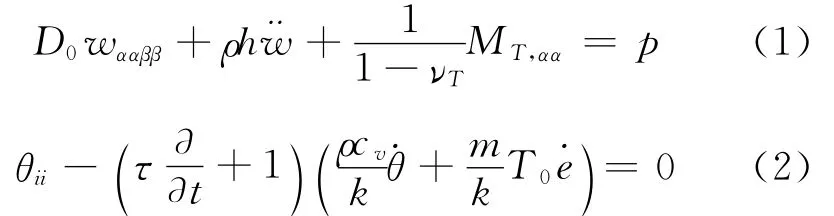
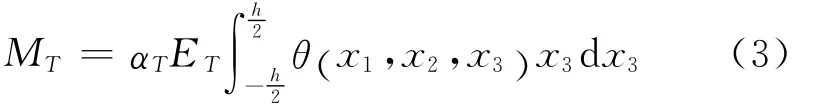
and wis the deflection.In the sequel we confine only to a simplified form of e,i.e.
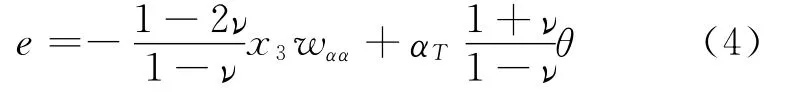
In the considered case of a pure small bending,Poisson′s ratio in Eq.(4)has the effective value dependent on the vibrational mode but it does not much differ fromνT.So,in the sequel we assume thatν=νT.For the model of interactions taken in the paper,we assume that the changes of temperature come only from vibrations of the plate and there is no thermal influence from surrounding.
The boundary conditions for Eqs.(1,2)are as follows(the plate is simply supported on all edges)[3]

The conditions(8-10)indicate that the temperature at lateral surfaces has been determined.At the remaining boundaries temperature varies because of alternate extension and compression of upper and lower fibres of the plate during vibrations.At those boundaries the free heat exchange has been assumed,so there is no temperature jump across upper and lower surfaces.In Eq.(10),ηis the surface heat exchange coefficient.
3 Free Vibrations of Thermoelastic Plate
Since we are interested in description of the thermoelastic damping of the rectangular thermoelastic plate with Poisson′s ratioν=νT∈(- 1;0.5)during free bending vibrations,solutions of Eqs.(1,2)with conditions(5-10)and p=0are looked in the forms.
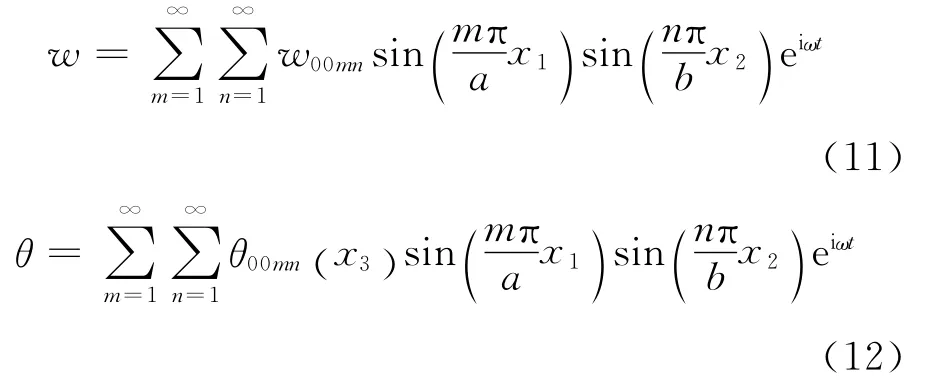
For the sake of simplicity,only first terms of expansions(11,12)are taken into considerations and denoted in the sequel that w0011=w00and θ0011=θ00.
Let′s take care of a material with the following properties:ET=1011N/m2,αT=3×10-6K-1,ρ=7 860kg/m3,k=58J/smK,cv=460J/kgK,τ=10-10s,h=0.005m,a=1m,b=1m,T0=100K.
From Fig.1it results that the first self-frequency achieves the highest values if the plate is in the auxetic state reaching minimum forν=0 and being almost constant for the natural state.
Fig.2indicates that the thermoelastic damping is the least in the auxetic state if Poisson′s ratio also increases depending not much on the plate thickness.
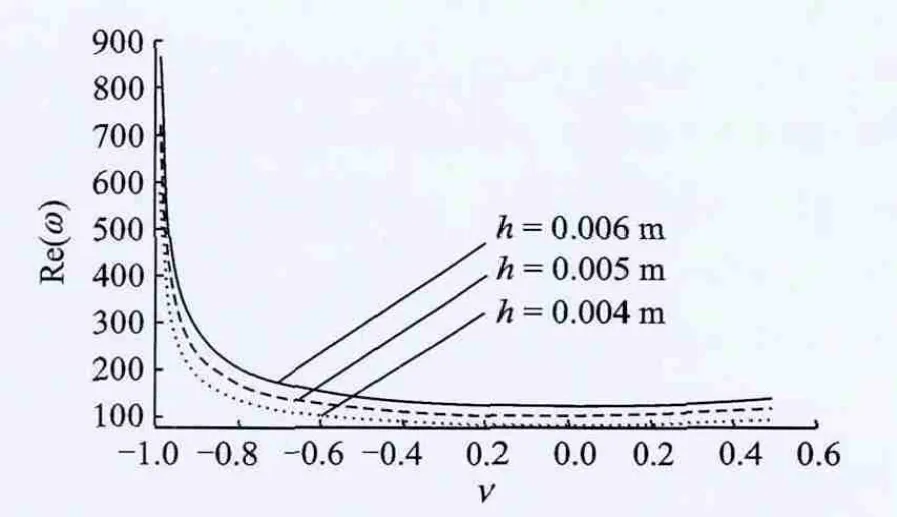
Fig.1 First self-frequency vs.Poisson′s ratio for different plate thickness
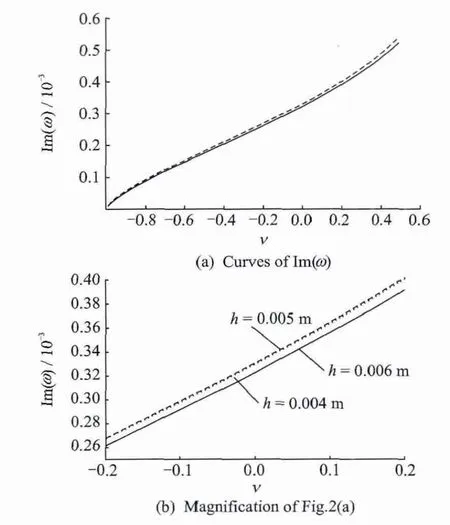
Fig.2 Thermoelastic damping vs.Poisson′s ratio for different plate thickness
The distribution of the temperature amplitude along the plate thickness is shown in Fig.3 both for the auxetic and natural material states.
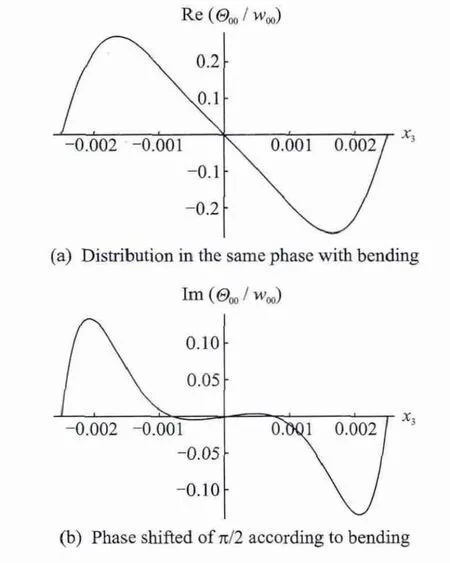
Fig.3 Distribution of temperature amplitude along the plate thickness
It can be seen from Fig.3(b)that if the temperature amplitude and bending are phase shifted ofπ/2,the thermal field in the reasonable big central region of the plate practically vanishes be-cause of the thermoelastic damping.Then the auxetic state becomes visible ifν→-1.
From Fig.4it results that the first self-frequency does not practically depend on the reference temperature(independent of the surrounding temperature).But the thermoelastic damping is strongly dependent on the surrounding temperature(Fig.5).

Fig.4 First self-frequency vs.Poisson′s ratio for three reference temperatures(T0=10,100,273K)
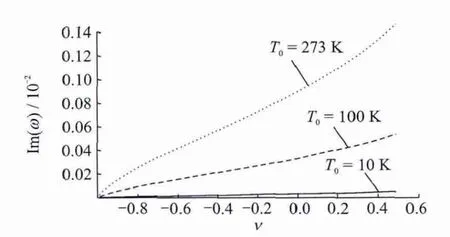
Fig.5 Thermoelastic damping vs.Poison′s ratio for different reference temperatures
And the thermoelastic damping almost linearly depends on the reference temperature T0for different values of Poisson′s ratio(Fig.6).
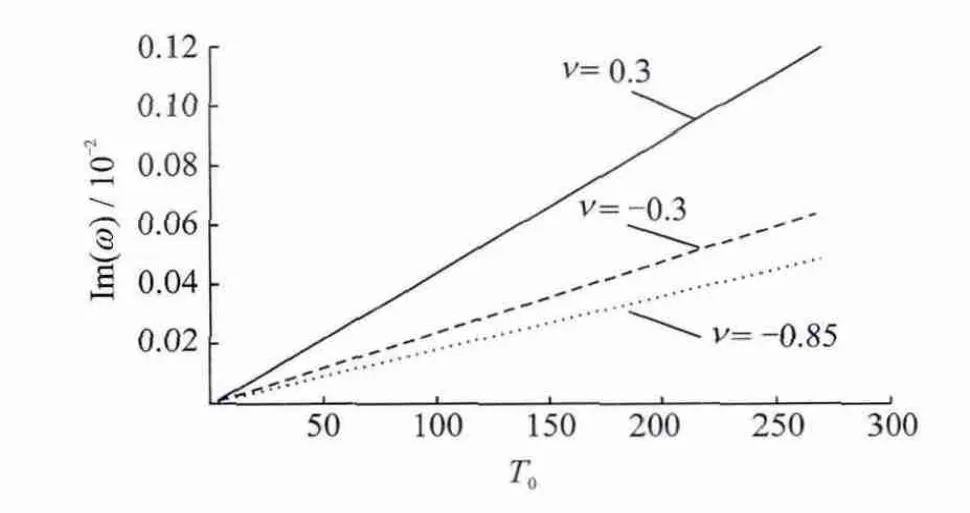
Fig.6 Thermoelastic damping vs.reference temperature for different Poisson′s ratios
4 Forced Vibrations
Now we are interested in description of a rec-tangular plate forced vibrations accompanied by the thermoelastic damping.The general solutions of Eqs.(1,2)with the boundary conditions Eqs.(6-10)are looked in the Eqs.(11,12)
Those solutions concern situation that our problem is 2D-3D,as it was mentioned before.For the case that the plate vibrations have forced character,we assume that the upper surface x3=is loaded by(see Eq.(1))
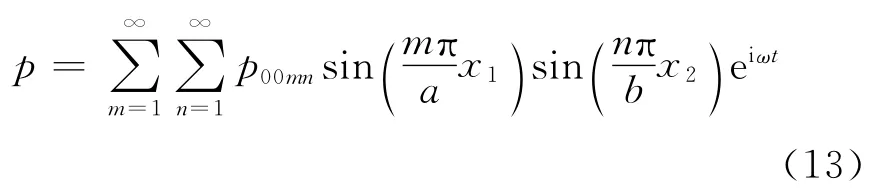
For the sake of simplicity,only first term of Eq.(13)is denoted by the sequel that p0011=p00.
Acknowledgements
The paper has been partially supported by MNSzW 2363/B/T02/2010/39and 21-418/2013/DS grants.
[1] Nowacki W.Thermoelasticity[M].Pergamon,Oxford:Addison-Wesley Pub.Co.,1962.
[2] Nowacki W.Dynamic problems of thermoelasticity[M].Noordhoff,Leyden:Springer,1975.
[3] Boley B A,Weiner J H.Theory of thermal stresses[M].Willey,New York:Dover Publications Inc.,1960.
[4] Noda N,Hetnarski R B,Tanigawa Y.Thermal stresses[M].New York:Taylor &Francis,2003.
[5] Zener C.Internal friction in solids.I[J].Physical Review,1937,52:230.
[6] Alblas J B.On the general theory of thermoelastic friction[J].Applied Scientific Research,Ser.A,1961,10:349.
[7] Alblas J B.A note of the theory of thermoelastic damping[J].Journal of Thermal Stresses,1981,4:333.
[8] Maruszewski B.Nonlinear thermoelastic damping in circular plate[J].ZAMM,1992,72:T75.
[9] Ignaczak J,Ostoja-Starzewski M.Thermoelasticity with finite wave speeds[M].New York:Oxford U-niversity Press,2010.
[10]Lifshitz R L,Roukes M L.Thermoelastic damping in micro-and nanomechanical systems[J].Physical Review B,2000,61:5600.
[11]Nayfeh A H,Younis M I.Modeling and simulations of thermoelastic damping in microplates[J].Journal of Micromechanics and Microengineering,2004,14:1711.
[12]Almgren R F.An isotropic 3-dimensional structure with Poisson′ratio=-1[J].Journal of Elasticity,1985,15:427.
[13]Lakes R.Foam structures with a negative Poisson′s ratio[J].Science,1987,235:1038.
[14]Wojciechowski K W.Two-dimensional isotropic system with negative Poisson′s ratio[J].Physics Letters A,1989,137:60.
[15]Novikov V V,Wojciechowski K W.Negative Poisson′s coefficients of fraktal structures[J].Physics of the Solid State,1999,41:1970.
[16]Pozniak A A,Kaminski H,Kedziora P,et al.A-nomalous deformation of constrained auxetic square[J].Reviews on Advanced Materials Science,2010,23:169.
[17]Kolat P,Maruszewski B,Wojciechowski K W.Solitary waves in auxetic plates[J].Journal of Non-Crystalline Solids,2010,356:2001.
[18]Kolat P,Maruszewski B,Tretiakov K V,et al.Solitary waves in auxetic rods[J].Physica Status Solidi(b),2011,248:148.
 Transactions of Nanjing University of Aeronautics and Astronautics2014年2期
Transactions of Nanjing University of Aeronautics and Astronautics2014年2期
- Transactions of Nanjing University of Aeronautics and Astronautics的其它文章
- Thin Film Lithium-Ionbatteries Crack Initiation Due to Thermal and Electric Effects
- Influence of Patch Side of Heat-Ray Absorbing Film on One-Dimensional Unsteady Thermal Stresses in Window Glass
- One-Dimensional-Unsteady Thermal Stress in Heat-Ray Absorbing Sheet Glass:Influence of a Sudden Weather Change
- General Solutions of Thermoelastic Plane Problems of Two-Dimensional Quasicrystals
- Temperature-Dependence of Microstructure Evolution in a Ferroelectric Single Crystal with Conducting Crack
- Problem of Circular Hole in Thermopiezoelectric Media with Semi-permeable Thermal Boundary Condition
