Temperature and carrier-density dependent excitonic absorption spectra of semiconductor quantum wires∗

WANG Ting-Dong(王廷栋)and HUAI Ping(怀平)

1Shanghai Institute of Applied Physics,Chinese Academy of Sciences,Shanghai 201800,China

2University of Chinese Academy of Sciences,Beijing 100049,China

3Key Laboratory of Nuclear Radiation and Nuclear Energy Technology, Chinese Academy of Sciences,Shanghai 201800,China

Temperature and carrier-density dependent excitonic absorption spectra of semiconductor quantum wires∗

WANG Ting-Dong(王廷栋)1,2and HUAI Ping(怀平)1,3,†

1Shanghai Institute of Applied Physics,Chinese Academy of Sciences,Shanghai 201800,China

2University of Chinese Academy of Sciences,Beijing 100049,China

3Key Laboratory of Nuclear Radiation and Nuclear Energy Technology, Chinese Academy of Sciences,Shanghai 201800,China

In this paper,we present a theoretical study on excitonic absorption spectra of one-dimensional semiconductor quantum wires.The carrier-carrier scattering is treated by the second Born approximation in the Markovian limit.The absorption spectra of different carrier densities and temperatures are discussed.The excitonic absorption peak position and width show complicated dependence on carrier density and temperature,indicating the importance of carrier-carrier scattering.The behavior can be understood by the cooperative effects of exchange self-energy and Coulomb correlation due to carrier-carrier scattering.

Semiconductor quantum wire,Exciton,Absorption,Carrier-carrier scattering

I.INTRODUCTION

Semiconductors,which have been used in radiation detection,are important materials for nuclear science and technology[1].Both in theoretical and experimental studies,low dimensional semiconductor structures have attracted much interest in recent years.In the longer term,compound semiconductor may be used as radiation detectors with higher performance and without the limits of strain[2,3].Thus the research about properties of low dimensional semiconductors is of great importance.

Semiconductor quantum wires(QWRs),in which electrons and holes are conf i ned in one direction,are typical onedimensional(1D)systems.The state of art QWR structures have been realized experimentally by molecular beam epitaxy with cleaved edge overgrowth and growth-interrupt annealing techniques[4–6].

In semiconductors,excitons are quasi-particles that form when electrons and holes are bound due to the Coulomb interactions.In 1D semiconductor structures,due to the quantum conf i nement,the excitonic effects on the optical spectra are greater than those in three-dimensional and two-dimensional structures[7–9].The signatures of excitons appear in the optical absorption spectra of direct-gap semiconductors,e.g. GaAs,showing a sharp peak several meV below the band gap energy.

Many-body effects play important roles in the lightsemiconductor interactions,such as excitonic nonlinearity, band-gap renormalization(BGR)and Coulomb screening. These complicated many-body phenomena can be revealed by optical spectra[10–12].In a typical experiment by simultaneously measurements of the absorption and photolumines-cence(PL)spectra,the peaks induced by excitons in low carrier density and plasma in very high density are observed[11].

It is therefore necessary to apply reasonable many-body theorytounderstandtheobservedfeaturesintheopticalspectraof QWRs.Under Hatree-Fock approximation,the Semiconductor Bloch Equations(SBEs)are good enough for calculationg the excitnoic nonlinearity,phase-space f i lling and the band gap renormalization[13,14].However,the absorption line width in SBEs is treated by just a phenomenological input parameter with the carrier-carrier scattering being neglected.Thus, a theory describing carrier-carrier scattering in a higher order approximation is needed.

In this paper,a theoretical method based on quantum kinetic equation is applied to the calculation.The carrier-carrier scattering is treated by the second Born approximation(SBA)in the Markovian limit[15–20].

II.MODEL AND NUMERICAL METHOD

In our scheme,the quantum kinetic equation for microscopic polarizationpkis given by[15–20]

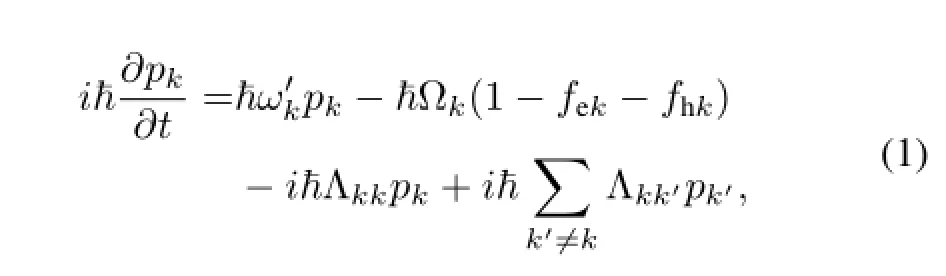
where

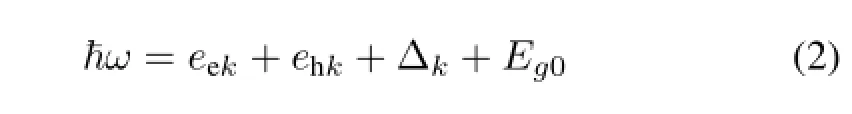
is the renormalized transition energy,is the corresponding renormalized transition frequency,and

is the exchange self-energy contribution to the renormalized band gap energy.The renormalized Rabi energy is

In Eqs.(1)-(4),kis the momentum,ħ is the Planck’s constant,eekandehkarethesingle-particleenergyofelectronsand holes.The band gap energy at zero carrier density is def i ned asEg0.Vis the effective Coulomb potential.In 1D systems,the Coulomb interaction is treated as effective interaction by averaging the three-dimensional Coulomb interactions over the electron and hole wave functions along the lateral directions. The distribution functions of electrons and holes are def i ned asfekandfhk.Under quasi-equilibrium conditions,both the distribution functions can be described as Fermi-Dirac functions and nearly time-independent.dcνis the dipole matrix element between the electrons and holes.˜ε0andωare the amplitude and frequency of electric part of the applied optical f i eld.The carrier-carrier scattering gives rise to the last two terms in the RHS of Eq.(1),which can be divided into diagonal(ħΛkk)and non-diagonal terms(ħΛkk′).

The diagonal and non-diagonal contributions due to carriercarrier scattering are

and

whereq=k′−k,VS(q)=V(q)/εqis the screened potential, withεqbeing the static dielectric function using Lindhard formula in plasmon-pole approximation[13].δa,bis Kronecker delta function andg(δε)=limν→0i/(δε+iν)is the Heitler-Zeta function,withδε=eak+ebk′−eak+q−ebk′−qandνbeing a small constant.

To solve Eq.(1)numerically,we convert it to the numerical solution of the equation of microscopic susceptibility

The effective Hamiltonian is denoted as

The absorption coeff i cient can be calculated by

whereandare thej-th left and right eigenvector corresponding to the effective HamiltonianHkefkf′,andEjis thej-th eigenvalue.The symbolImmeans takingthe imaginary partof a complex function.Since the effective Hamiltonian is complex,the eigenvalues and eigenvectors are complex numbers and complex vectors,respectively.Different from the situation of Hartree-Fock level,no phenomenological damping parameter is needed here.The absorption line width is attributed to the complex part ofEj.

Numerical calculations are carried out for a typical rectangular cross-section GaAs quantum wire with the following parameters:Eg0=1.5eV,the dielectric constantε0=13.74, the cross-section lengthlx=14nm and widthly=6nm,anddcν=4.33eA˚.The effective masses of electrons and holes areme=0.0665m0andmh=0.457m0,wherem0is the mass of an electron in free space.

III.RESULTS AND DISCUSSION

Figure 1 shows the calculated absorption spectra of the GaAs QWR for different carrier densities atT=60K and different temperatures of atne=nh=0.2×106cm−1.A strong absorption about 20meV below the bang gap is ascribed to excitons.In Fig.1(a),the intensity of excitonic peak decreases with increasing carrier density,with an almost constant peak position energy.stays nearly constant.On the other hand, SBEs theory predicts a large red shift in excitonic absorption peak with increasing carrier density.This can be understood by the overestimate of renormalization of the band gap.The present approach shows constant excitonic absorption peak, which agree well with experiment results.Since exciton is an electrically neutral quasi particle,the Coulomb interaction has little dependence on the carrier density resulting in a constant exciton energy.At the carrier density ofne=nh= 0.2×106cm−1,when the temperature increases,the excitonic absorption peak shows a red shift.Moreover,the peak width increases with temperature,indicating stronger carrier-carrier scattering at higher temperatures.From the experimental results of a QWR by the systematic micro-PL method,the excitonic peak shows its stability[11]which is a good proof of our theoretical results.

Figure 2 shows data of the peak position energy atT=60K (Fig.2(a))and at carrier density ofne=nh=0.2×106cm−1(Fig.2(b)).Each error bar in the minus and plus direction denotes the lower and upper half-widths of the peak.At constant temperature of 60K,the peak energy changes little,and the peak width increases slightly,with carrier density changing. At constant carrier density ofne=nh=0.2×106cm−1,the peak energy decreases with increasing temperature.Therefore, temperature affects the excitonic absorption peak energy more than the carrier density.

Fig.1.(Color online)Absorption spectra of a rectangular GaAs semiconductor quantum wire:(a)different carrier densities atT=60K;(b) different temperatures at carrier density ofne=nh=0.2×106cm−1.

Fig.2.(Color online)Excionic peak energy at(a)T=60K and(b)ne=nh=0.2×106cm−1.

Fig.3.(Color online)Exchange self-energy,Λkatk=0 for(a)temperatureT=60K and(b)carrier densityne=nh=0.2×106cm−1.

For direct-gap semiconductors,the band gap is def i ned asenergy difference between conduction band and valence bandatk=0,i.e.center of the Broullion zone.Fig.3 shows the exchange self-energy atT=60K(Fig.3(a))and at carrier density ofne=nh=0.2×106cm−1(Fig.3(b)).The energy depends differently on the carrier density and temperature.As the contributions from carrier-carrier scattering(Eq.(5)and (6))are considered,the imaginary part of diagonal and nondiagonal terms will add additional energy shift for band gap. The exchange self-energy,the energy shift from scattering together with the binding energy of excitons will f i nally determine the excitonic peak position and width,as shown in Fig.2.

IV.CONCLUSION

In conclusion,a theoretical study is done on the absorption spectra of a GaAs QWR in different carrier densities or different temperatures.The excitonic absorption peak position and width show complicated behaviors as the temperature or carrier density varies.This can be understood by the cooperative effects of exchange self-energy and Coulomb correlation due to carrier-carrier scattering.

[1]Lutz G.Semiconductor Radiation Detectors:Device Physics, Berlin(Germany):Springer–Verlag,1999,79–331.

[2]Ariyawansa G.Ph.D.Thesis,Georgia State University,2007.

[3]Owens A,Peacock A.Nucl Instrum Methods A,2004,531:18–37

[4]Okano M,Liu S M,Ihara T,et al.Appl Phys Lett,2007,90: 091108.

[5]Yoshita M,Liu S M,Okano M,et al.J Phys-Condens Mat,2007,19:295217.

[6]Okano M,Yoshita M,Akiyama H,et al.Phys Status Solidi C, 2011,8:20–23.

[7]Ogawa T,Takagahara T.Phys Rev B,1991,44:8138–8156.

[8]Loudon R.Am J Phys.1959,27:649–655.

[9]Rossi F,Molinari E.Phys Rev Lett,1996,76:3642–3645.

[10]Akiyama H,Pfeiffer L N,Yoshita M,et al.Phys Rev B,2003,67:041302.

[11]HayamizuY,YoshitaM,TakahashiY,etal.PhysRevLett,2007,99:167403.

[12]Akiyama H,Yoshita M,Hayamizu Y,et al.Physica E,2008,40: 1726–1728.

[13]Benner S,Haug H.Europhys Lett,1991,16:579–583.

[14]Huai P and Ogawa T.J Lumin,2006,119–120:468–472.

[15]Jahnke F,Kira M,Koch S W,et al.Phys Rev Lett,1996,77: 5257–5260.

[16]Chow W W,Smowton P M,Blood P,et al.Appl Phys Lett,1997,71:157–159.

[17]Chow W W,Knorr A,Hughes A,et al.IEEE J Sel Top Quant, 1997,3:136–141.

[18]Girndt A,Jahnke F,Knorr A,et al.Phys Status Solidi B,1997,202:725–739.

[19]Koch S W,Kira M,Meier T.J Opt B-Quantum S O,2001,3: R29–R45.

[20]Chow W W,Koch S W.Semiconductor–Laser Fundamentals: Physics of the Gain Materials.Berlin(Germany):Springer–Verlag,1999,107–149.

10.13538/j.1001-8042/nst.25.010201

(Received September 16,2013;accepted in revised form January 15,2014;published online February 20,2014)

∗Supported by the National Basic Research Program of China(No. 2010CB934504)and the National Natural Science Foundation of China (No.10874197)

†Corresponding author,huaiping@sinap.ac.cn