Impact of Convective Momentum Transport by Deep Convection on Simulation of Tropical Intraseasonal Oscillation
LING Jian, and LI Chongyin
1) The State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics, Institute of Atmospheric Physics, Chinese Academy of sciences, Beijing 100029, P. R. China
2) Institute of Meteorology and Oceanography, PLA University of Science and Technology, Nanjing 211101, P. R. China
Impact of Convective Momentum Transport by Deep Convection on Simulation of Tropical Intraseasonal Oscillation
LING Jian1),*, and LI Chongyin2)
1) The State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics, Institute of Atmospheric Physics, Chinese Academy of sciences, Beijing 100029, P. R. China
2) Institute of Meteorology and Oceanography, PLA University of Science and Technology, Nanjing 211101, P. R. China
This paper focuses on the impacts of convective momentum transport (CMT) on simulations of the tropical intraseasonal oscillation (TIO) in SAMIL. Two sets of experiments are performed, which give different reality of the Madden-Julian Oscillation (MJO). The Tiedtke cumulus parameterization scheme is used for all experiments. It is found that simulations of the TIO can be influenced by CMT, and the impacts on the simulated TIO depend on the model capability in simulating the MJO. CMT tends to have large influences to the model that can simulate the eastward propagation of the MJO. CMT can further influence the long-term mean of zonal wind and its vertical shear. Zonal wind suffers from easterlies biases at low level and westerlies biases at upper level when CMT is introduced. Such easterlies biases at low level reduce the reality of the simulated tropical intraseasonal oscillation. When CMT is introduced in the model, MJO signals disappear but the model’s mean state improves. Therefore, a more appropriate way is needed to introduce CMT to the model to balance the simulated mean state and TIO signals.
Madden-Julian Oscillation (MJO); convective momentum transport (CMT); SAMIL
1 Introduction
The Madden-Julian Oscillation (MJO, Madden and Julian, 1971, 1972), the dominant part of tropical intraseasonal oscillation (TIO), has important effects on the weather and climate systems in and out of the tropic region (Wang and Rui, 1990; Paegle et al., 2000; Zhang and Gottschalck, 2002; Zhou and Chan, 2005; Li et al., 2012). Its characteristics have been well documented in several reviews (Zhang, 2005; Lau and Waliser, 2012). The MJO is characterized by its zonal planetary scale (zonal wavenumbers 1–5), baroclinic structure, and eastward propagating convection coupled with the large-scale circulation from the Indian Ocean to central Pacific with a period range of 30–60 days. However, most state-of-theart general circulation models (GCMs) fail to reproduce the key features of the MJO (Slingo, 1996; Lin, 2006; Kim, 2009) and the reason cannot be fully explained by existing MJO theories. This reflects the lack of understanding of the fundamental MJO dynamics.
Several factors influencing MJO simulations have been proposed, such as cumulus parameterization, resolution, model mean states, and air-sea interaction (Slingo, 1996; Waliser et al., 1999; Wang and Schlesinger, 1999; Hendon et al., 2000; Inness et al., 2003; Ling et al., 2009; Jia et al., 2009, 2010; Ling et al., 2013). Cumulus parameterization is usually thought to be the key factor to determine the quality of the simulated MJO (Wang and Schlesinger, 1999; Maloney and Hartmann, 2001). Convection, especially deep convection, affects the tropical atmospheric circulation system mainly through two processes: latent heating released from condensation and vertical convective momentum transport (CMT). Several studies have addressed the impacts on MJO simulations by the vertical structure of diabatic heating (Li et al., 2009; Ling et al., 2013) as well as CMT (Ling et al., 2009; Miyakawa et al., 2012). We further study the influence of CMT on MJO simulations in this study in a revised model that can simulate the eastward propagation of MJO.
The importance of CMT in the atmospheric general circulation was recognized in the 1970s. Houze (1973) found the contribution of CMT to atmospheric angular momentum is as important as the large-scale transport. Stevens (1977) found that the CMT is an important mechanism of momentum exchange in the tropic, and it is indispensable for simulating a realistic tropical circulation. Helfand (1979) showed that simulated mean meridional wind is closer to the observation when CMT is included. This result was confirmed by Ose et al. (1989). Li (1984) pointed out that CMT can act like Ekman pumping in the genesis of typhoon and the development of the ITCZ. Tiedtke (1989) showed that CMT has strong impact on the rotational flow in a forecasting model. Some numeri-cal studies show that the atmospheric mean state can be improved by introducing CMT (Zhang and McFarlane, 1995; Gregory et al., 1997; Inness and Gregory, 1997). It is possible to better reproduce the mean state of the atmosphere circulation by including CMT, but the simulated MJO might be deteriorated due to weaker westerlies in the upper troposphere over the tropical eastern Pacific and weaker precipitation over the North Pacific (Inness and Gregory, 1997).
Few studies have, however, focused on the influence of CMT on the GCM’s capability of simulating the MJO. Miyakawa et al. (2012) investigated CMT in rainbands within a MJO event simulated by a global nonhydrostatic model and proposed that CMT delays the eastward propagation of the low- to mid-troposphere westerly wind, hence delaying the eastward migration of the convectively favorable region and reducing the propagation speed of the MJO. Ling et al. (2009) studied the influence of CMT in the Tiedtke (1989) scheme on MJO simulations using Community Atmospheric Model version 2 (CAM2) and SAMIL (Spectral Atmosphere Model of IAP LASG, see section 2a), and found that MJO simulations were influenced by CMT in CAM2. However, CMT did not show clear influence to the MJO simulation in SAMIL. Such slight influence of CMT may be due to the poor MJO simulation capability of SAMIL. Ling et al. (2013) found the possible reason for poor MJO simulation capability of SAMIL is the latent heating peak in the planetary boundary layer (PBL). Once the heating peak of shallow convection produced by cumulus parameterization is removed, the model can well simulate the eastward propagation signals of the MJO. This gives us a chance to reevaluate the influence of CMT on the simulated MJO signal in SAMIL, especially focusing on deep convection in the experiments where heating from shallow convection is removed.
This study is the follow-up work of Ling et al. (2009; 2013). In order to explore how CMT influences MJO simulations by SAMIL, sensitive experiments were designed. The model, the configuration of the experiments, and the data used in this study are described in section 2. Model results are presented in section 3. A summary and discussion are given in section 4.
2 Model and Methodology
2.1 Model
The atmospheric general circulation model (AGCM) used in this study is a spectral model (refered to as SAMIL) which was adopted from Simmonds (1985) and then developed at the State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics (LASG) in the Institute of Atmospheric Physics (IAP) of the Chinese Academic of Science (CAS). It is one of the atmospheric components of the Flexible Global Ocean-Atmosphere-Land System model (FGOALS) participating in the Intergovernmental Panel on Climate Change Fourth Assessment Report (IPCC AR4) and is frequently used in climate studies (Jia et al., 2008; Li et al., 2009; Jia et al., 2010; Wang et al., 2012). It employs a unique dynamic core to reduce systematic errors due to the truncation and topography. The horizontal resolution is a rhomboidal truncation with maximum wavenumber 42 (R42, 128× 108 Gaussian grid points, about 2.8125˚ longitude×1.66˚ latitude). There are 26 hybrid vertical layers extending from the earth’s surface to 2.19 hPa. The parameterization package includes the Endwards and Slingo (1996) scheme for radiation, the Slingo (1980, 1987) scheme for cloud diagnosis, and the Holtslag and Boville (1993) scheme for the boundary layer. A simplified version of the Simple Biosphere model (Sellers et al., 1986) is used for land surface processes (Xue et al., 1991). A semi-implicit scheme with a time step of 15 min was used. Further details of SAMIL are available in Wu et al. (1996).
2.2 Cumulus Parameterization Scheme
The Tiedtke (1989) scheme was first implemented in SAMIL by Song (2005). It is a mass flux convection scheme, which can represent shallow, deep, and midlevel convections. However, only one type of convection can occur at each time step and grid point. An ensemble of clouds for each type of convection is assumed to consist of updrafts and downdrafts. Mid-level convection, with its cloud base above the PBL, mainly occurs in rain bands at warm fronts and in the warm sector of extratropical cyclones. Deep convection mostly occurs under the conditional instability of deep layer and larger-scale moisture convergence. Shallow convection is mostly initiated in an undisturbed flow (in the absence of large-scale convergence flow), such as trade wind cumuli under a subsidence inversion.
The vertical transport of horizontal momentum by convection is introduced by adding the following two equations to the large scale zonal and meridianal wind component equations respectively.
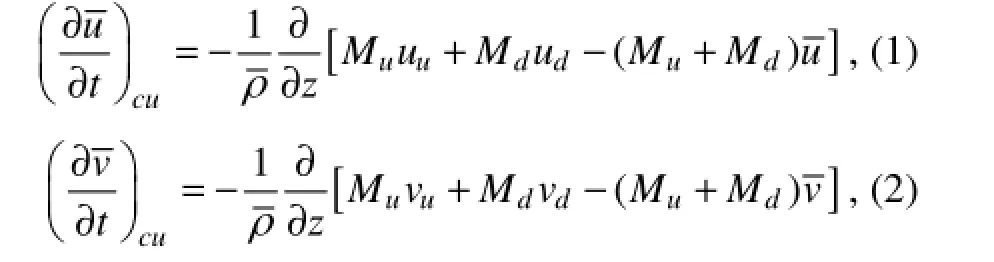
where u and v are the horizontal wind components, ρ the density of the air, M the mass flux. The overbar denotes averages over the grid box, subscript cu the contribution from cumulus convection, u and d contributions from updrafts and downdrafts, respectively.
The vertical transport of momentum was treated in the same way as thermodynamical parameters disregarding cumulus-scale pressure effects (Scheider and Lindzen, 1976). However, the entrainment rate for momentum variables is larger than that for thermodynamics in order to make the momentum inside the clouds closer to the momentum of the environmental air than an entrainment plume without pressure perturbation would give. The details are given by Tiedtke (1989) and Nordeng (1994).
2.3 Experiment and Analysis
Three additional sensitive experiments were designed to explore the impact of CMT on MJO simulations besides the default setting of SAMIL (control run, without CMT, refered to as CTNMT). The control run with CMT (refered to as CTCMT) was first conducted to evaluate the impact of CMT on the MJO simulations. The SAMIL without PBL heating peak from shallow convection (refered to as no shallow heating run thereafter) was adopted from Ling et al. (2013) and two runs with and without CMT was applied to it (refered to as NSCMT and NSNMT). Detailed information for the no shallow heating run is available in Ling et al. (2013). It is known that CMT has little impact on MJO simulations in SAMIL under its default configuration. The experiments of no shallow heating were used to check whether CMT has impact on MJO simulation in SAMIL when the model can reproduce good eastward propagation signal of MJO.
All the experiments were integrated for 11 years. Initial conditions were based on NCAR/NCEP (Kalnay, 1996) reanalysis. Climatology monthly mean sea surface temperature and sea ice were used as the lower boundary conditions. Only the last 10 years of data were used to diagnose the simulated MJO.
Main diagnostic variables included the zonal wind and latent heating (LH) produced by the cumulus parameterization and large-scale condensation. Precipitation from the no shallow heating runs were not related to the LH profile due to the modification of LH profiles at each time step (see details in Ling et al., 2013). A variable, EPR, derived from latent heating, was later used in place of precipitation. It is linearly related to vertically integrated latent heating. Its value represents the amount of the precipitation corresponding to a specific latent heating profile:
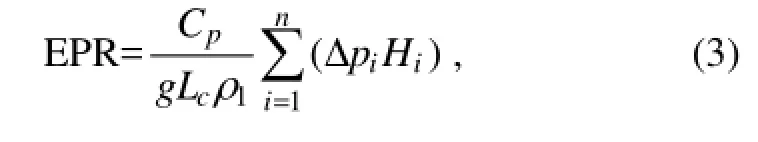
where Cpis the specific heat capacity of dry air, i the index for vertical levels, Δpithe pressure depth, the latent heating tendency at level i, Lcthe latent heat of condensation at 0℃, ρ1the density of liquid water, and n the total number of vertical levels in the troposphere.
Anomalous time series were first obtained by removing the 10 years daily climatology, and then averaged over the tropics (15˚N-15˚S). The variability of TIO was then obtained by applying a band-pass filter (time period of 30 -90 d and zonal wavenumber of 1-10) to the anomalous time series following Wheeler and Kiladis (1999) except the spectral coefficients for both eastward and westward propagation are retained in this paper. It is known that only the eastward spectra of TIO incoherent with their westward counterparts belong to eastward propagating perturbations, which is the key characteristic of MJO (Hayashi, 1979). Therefore, the filtered signal was regarded as the TIO signal in this study, and only its eastward propagating component is regarded as MJO. Space-time spectral and linear regressions were used to analyze the zonal propagating features of simulated TIO.
3 Results
3.1 TIO Signals
The TIO as well as its most well known component MJO have been studied by many previous studies. Characteristics of MJO, such as its zonal scale, periods, eastward propagation, and structure from observations have been documented in many reviews (Zhang, 2005; Lau and Waliser, 2012). They are not repeated in this study.
Time-space spectra of unfiltered zonal wind at 850 (U850) and 200 hPa (U200) and EPR from four simulations are shown in Fig.1. The spectra for U850 and U200 from the CTNMT run (Figs.1a and b) show peaks in the intraseasonal band, but there is no obvious discrepancy in the intensity of spectra between the eastward and westward components. In contrast, the intraseasonal spectral peaks of zonal wind (U850 and U200) from the NSNMT run are well separated from the lower and higher frequencies and their eastward components are obviously larger than the westward counterpart (Figs.1g and h). These results suggest an eastward propagating intraseasonal signal in the NSNMT run. Furthermore, The EPR spectrum for the NSNMT run also shows greater power and a larger wavenumber range (from 1 to 3) in the intraseasonal period than those in the CTNMT run.
Generally speaking, the power spectra from CTCMT and NSCMT become weaker than those from no CMT runs, especially in the 30-60 d period. The spectral intensity of the zonal wind in CTCMT (Figs.1d and e) in the intraseasonal band reduces nearly the same amount for both eastward and westward components compared to CTNMT. However, the spectral intensity of the zonal wind in the intraseasonal band in the NSCMT run (Figs. 1j and k) only reduces in the eastward component and almost no change in the westward component. The results suggest that the zonal propagating direction of the intraseasonal oscillation in the CTCMT run might be the same as CTNMT run, while the eastward propagation signal of the intraseasonal oscillation in the NSCMT run may become, if it still exists, weak compared to that in the NSNMT run.
In order to further analyze the zonal propagating characteristics of the intraseasonal oscillation, a linear lag regression upon EPR at 90˚E was applied to MJO bandfiltered U850 and EPR for all simulations. The significant level of 90% was applied using the Student’s t-test. The results (Fig.2) confirm what the time-space spectra shows in Fig.1.
Neither U850 nor EPR from the CTNMT run shows any eastward propagating signal, and they even show weak westward propagating signals related to the equatorial Rossby wave. Both U850 and EPR from NSNMT show obviously eastward propagating signals from the Indian Ocean to the central Pacific.
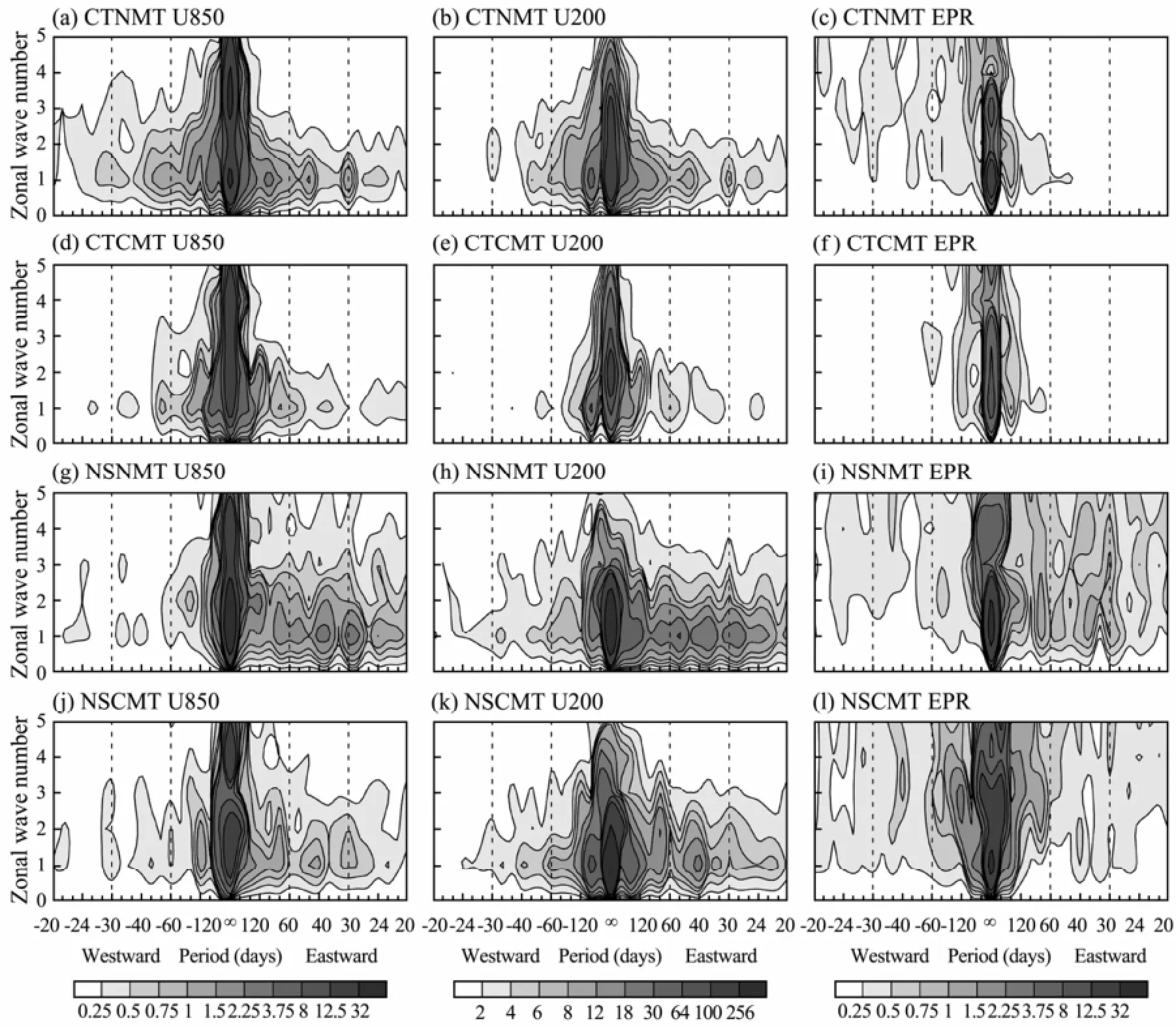
Fig.1 Time-space spectra of U850 (left column), U200 (middle), and EPR (right) averaged from 15˚S to 15˚N from (top to bottom row) control run without (CTNMT) and with CMT (CTCMT), and no shallow heating tuns (NSNMT and NSCMT).
Amplitudes of zonal propagating signals of U850 and EPR in the CTCMT run become weaker, but the direction is still the same compared to the CTNMT run. However, their zonal propagating characteristics change dramatically in the NSCMT run compared to the NSNMT run. Not only the amplitudes of U850 and EPR reduce, but also their eastward propagating signals disappear. These results are further confirmed using another reference point (150˚E) for regression over the western Pacific. It is clearly shown that the impact of CMT on TIO simulations can be very different using different configurations of the model. The CMT impacts on the TIO simulations are weak if the model cannot realistically simulate the eastward propagation of TIO (MJO). If the model can produce realistic MJO signals, such as its periods and eastward propagation signals, the impact of CMT on the simulated MJO might be strong.
Horizontal distributions of the standard deviation of the zonal wind at 850 hPa (U850) of the TIO are shown in Fig.3 over the tropical Indian Ocean-Maritime Continent-Pacific Ocean, where the eastward propagation signal of MJO dominates. It clearly shows that CMT has different impacts on the simulated TIO signals in different Hemispheres. The maximum center of the zonal wind in the Southern Hemisphere is located between the Maritime Continent and Australia around 120˚E in all simulations. However, the variability is slightly larger in the NSCMT run than in the NSNMT run, while slightly weaker in the CTCMT run than the CTNMT run. After introducing CMT, the maximum centers of the zonal wind over the western Pacific in both CTCMT and NSCMT runs disappear, and the amplitude over the Indian Ocean also decreases in the Northern Hemisphere. Furthermore, the maximum center over the tropical Indian Ocean, which only exists in the NSNMT run, disappears in the NSCMT run. The disappearance of these two maxima centers over the Indian Ocean and western Pacific Ocean might be the reason for no eastward propagating signal in the NSCMT run.
Other diagnostic methods suggested by the CLIVAR Madden–Julian Oscillation Working Group (CLIVAR 2009) were also employed to examine the TIO signal and its eastward propagating component (MJO) in all simulations. An EOF analysis was applied to the intraseasonal zonal wind at 850 hPa averaged within the tropics (15˚N-15˚S) in CTCMT run. It yields only one dominant modeof zonal wavenumber one with fractional variances of 35.88%. Similarly, there is only dominant EOF mode for the CTNMT run albeit with higher fractional variance (41.68%). Thus, strong stationary oscillation of zonal wavenumber one dominates the TIO in the zonal wind in both runs (CTCMT and CTNMT). The NSNMT run produced a pair of leading mode of zonal scale of wavenumber one, with their respective fractional variance of 25.15% and 23.70%. The correlation between the time series of these two leading modes is the highest at a lag of 11 d with a significant level above 95%, suggesting eastward propagation with a period about 44 d. Only one dominant mode with fractional variance of 27.94% is found in the NSCMT run.
Together with the results from Ling et al. (2009), this study demonstrates the following changes in TIO simulations when CMT is included: I) the amplitude of TIO becomes weak, II) the eastward propagating signal of MJO in the no shallow heating run (NSCMT) disappears, and III) the impacts from I) and II) are larger when the model produces more realistic eastward propagating signals of the MJO.
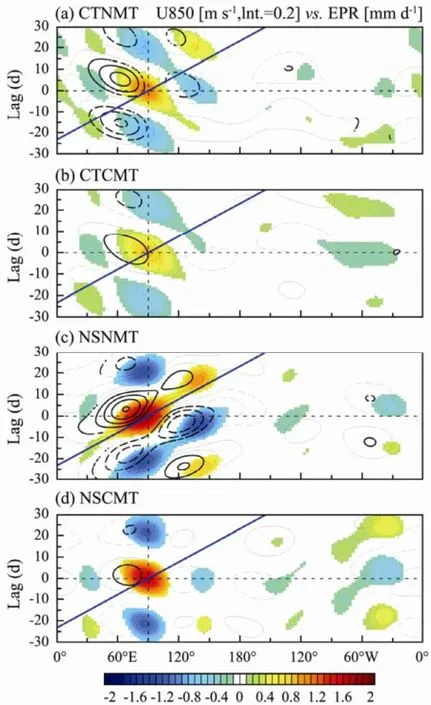
Fig.2 Lag regression of MJO band filtered U850 (contour, interval 0.2 m s-1) and EPR (shaded, mm d-1) upon EPR at 90˚E (0 d) from (top to bottom row) control run without (CTNMT) and with CMT (CTCMT), and also no shallow heating run (NSNMT and NSCMT). All the data were first averaged over 15˚S-15˚N. Dashed contours for negative values and zero contours were omitted. Only results passing a significant test with the 90% confidence level were plotted for EPR, highlighted by thick contours for U850. The blue thick solid lines represent the 5 m s-1eastward propagation speed.
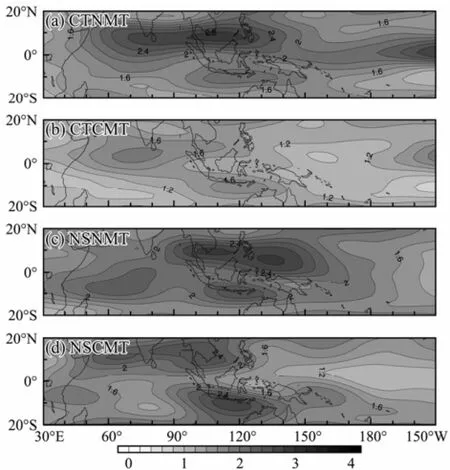
Fig.3 Horizontal distributions of standard deviation of intraseasonal zonal wind (m s-1) at 850 hPa from (top to bottom row) control run without (CTNMT) and with CMT (CTCMT), and also no shallow heating run (NSNMT and NSCMT).
3.2 Mean State
The mean state has been considered crucial to the dynamics of the MJO in many previous studies. Simulated MJO-like signals tend to be stronger in models with more realistic mean precipitation (Slingo, 1996). The mean vertical wind shear and low-level zonal wind also play important roles in MJO simulations (Hendon, 2000; Kemball-Cook et al., 2002; Inness et al., 2003). Previous studies suggested that the MJO appears to favor the condition of low-level mean westerlies in both simulations (Inness et al., 2003) and observations (Zhang and Dong, 2004). However, the exact role of the mean state in MJO simulations has yet to be quantified.
In order to explore the reason for the different CMT impacts on MJO simulations in the control run and the no shallow heating run, the horizontal distribution of mean EPR from all simulations are shown in Fig.4. The main reason for diagnosing EPR instead of precipitation is that EPR is consistent with the latent heating in the no shallow heating runs without (NSNMT) and with (NSCMT) CMT (Ling et al., 2013).
Mean EPR from both control runs (CTCMT and CTNMT) shows the erroneous double ITCZ over the tropical eastern Pacific and Indian Oceans, which is more severe than in most other AGCMs. There is no obvious difference in EPR between the CTCMT and CTNMT runs albeit slightly weaker amplitude in CTCMT. It is very interesting that EPR over the Northern Hemisphere isenhanced after latent heating from shallow convection is removed in NSNMT compared to CTNMT. The reason for the enhancement of EPR over the Northern Hemisphere is unknown. It could be related to the enhanced Indian Summer Monsoon in NSNMT due to enhanced deep convection (Ling et al., 2013). In the no shallow heating runs, mean EPR over the equatorial Indian Ocean and western Pacific almost disappears in the NSCMT run compared to the NSNMT run, while the amplitude of EPR over the Arabian Sea and the Bay of Bengal increases in NSCMT. EPR between the Maritime Continent and Australia around 120˚E is also enhanced after introducing the CMT in NSCMT, which may correspond to the enhanced intraseasonal oscillation in the zonal wind at 850hPa (Fig.3d). All enhanced EPR in the NSCMT run tends to occur over coast regions, possibly due to the land-sea distribution.
The long-term means of zonal wind at 850 and 200 hPa averaged over 15˚S-15˚N are shown in Fig.5. The longitudinal distribution of the zonal wind is different between the control run and the no shallow heating run without CMT (CTNMT and NSNMT). The difference in U850 may be caused by the removal of the boundary layer heating peak in NSNMT, while the difference in U200 may be due to the large-scale circulation responding to the enhanced convective center over the northern Indian Ocean and western Pacific (Fig.4b). The cause of the different zonal wind distributions between the CTNMT and NSNMT runs is not the main concern of this study. Our main concern is the CMT impact on the distribution of the zonal wind.
The low-level zonal wind (U850) suffers from easterly biases in the runs with CMT (CTCMT and NSCMT) comparing to that without CMT (CTNMT and NSNMT) (Fig.5a). However, westerly biases exist in the upper level (U200) over the Indian and Pacific Oceans in the runs with CMT (Fig.5b). This result is consistent with the previous study indicating that the MJO favors low-level westerlies (Zhang and Dong, 2004). The runs with CMT (CTCMT and NSCMT), which tends to simulated poorer and weaker MJO signals, suffer from easterlies biases at the low level compared to the runs without CMT (CTNMT and NSNMT). Miyakawa et al. (2012) also foundThat CMT contributes negatively to the westerly tendency between 2 and 6.5 km, and to the easterly tendency above 11 km in rainbands of an MJO event in a global nonhydrostatic model.
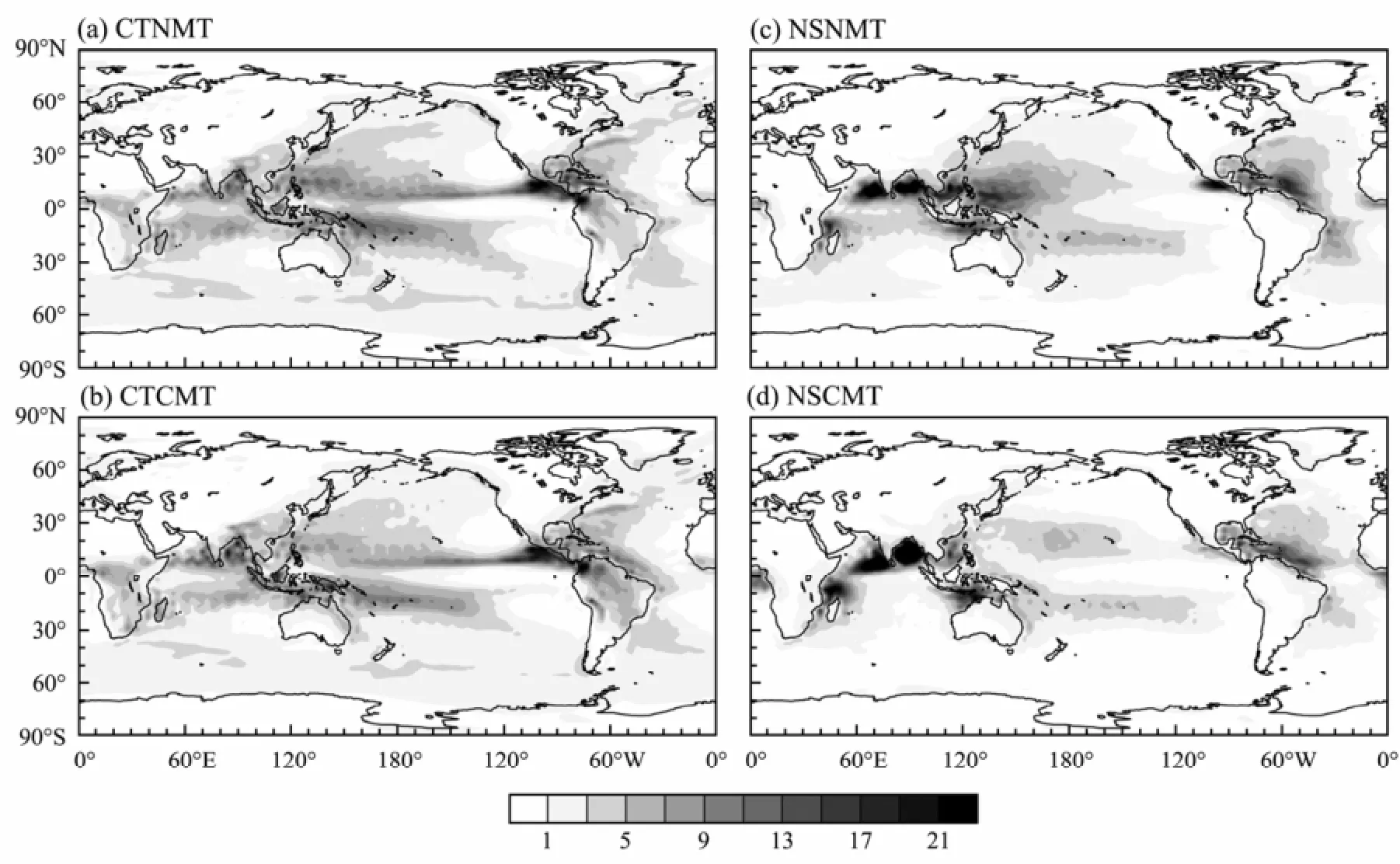
Fig.4 Horizontal distributions of mean EPR (mm d-1) from (a) control run and (b) no shallow heating run without CMT, and (c), (d) with CMT.
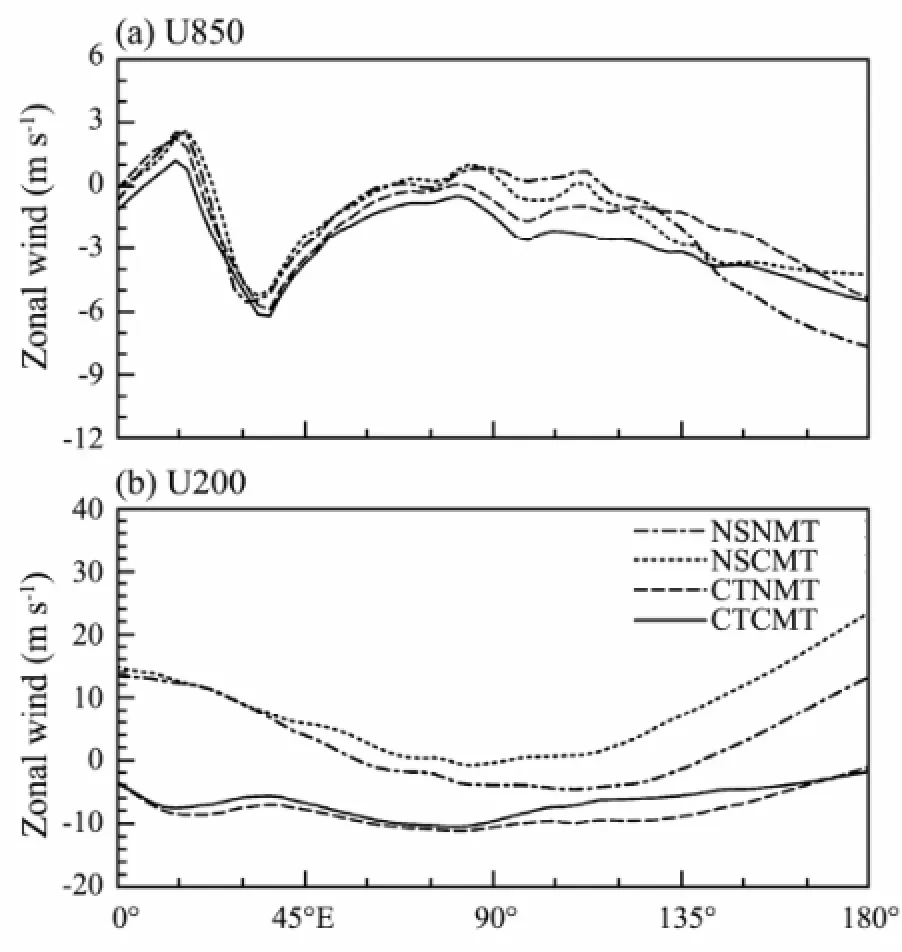
Fig.5 Longitudinal distributions of mean zonal wind (m s-1) at (a) 850 hPa and (b) 200 hPa from all simulations. All are averaged over 15˚S-15˚N.
CMT reduces the vertical wind shear in large-scale convection. Fluctuations in daily zonal wind shear between 850 hPa and 200 hPa over the region where the MJO propagation signal is dominant (60˚E-180˚, 10˚S-10˚N) were calculated (not shown). They are larger in all no CMT runs (CTNMT and NSNMT) than in CMT runs (CTCMT and NSCMT). This means that the appearance frequency of deep convection in the no CMT runs is larger than that in the CMT runs. These results indicate that less deep convection, which usually generates the vertical wind shear on synopic time scales, is produced when CMT is included.
3.3 Heating Profiles
The importance of the vertical structure of diabatic heating to MJO simulations has been explored in previous studies (Li et al., 2009; Ling et al., 2013). Mean latent heating profiles from all simulations averaged over the tropical region (15˚S-15˚N) are shown in Fig.6. Total latent heating from CTNMT shows large values at the major convection centers, such as those over the tropical eastern Indian Ocean-Maritime Continent-western Pacific Ocean, South America, and Africa. The peaks of latent heating over these convection centers occur at 500 hPa. These features are almost the same as those from Tropical Rainfall Measuring Mission (TRMM) retrievals and reanalyses (Zhang, 2010; Ling and Zhang, 2011, 2012). The most distinct difference between the CTNMT and NSNMT runs is that convection over the Indian Ocean, Maritime Continent, and western Pacific is enhanced, which also can be found in the horizontal distribution of EPR (Fig.4). These are the regions where the MJO signal dominates. The difference of the latent heating profiles between the CTNMT and NSNMT runs within the boundary layer is discussed in Ling et al. (2013). The distribution of latent heating form the CTCMT run is almost identical to that from the CTNMT run, albeit slightly weaker for all the longitudes. Latent heating from the NSCMT run becomes much weaker over the Indian Ocean and western Pacific, consistent with the horizontal distribution of the intraseasonal variability of the zonal wind at 850 hPa and the long term mean of EPR. As pointed out by Ling et al. (2013), the reason for no eastward propagation signal in the CTNMT run is that the boundary layer heating peak prevents moisture from being transported into the free atmosphere from the boundary layer. Less moisture within the free atmosphere does not favor the initiation of deep convections over the tropics. Therefore, there is no MJO signal in CTNMT. It is also clearly shown that latent heating becomes weaker in CTCMT and NSCMT. It means that CMT in the Tiedtke scheme has a negative influence on simulations of deep convection. Deep convection may be harder to be generated or maintained when CMT is included.
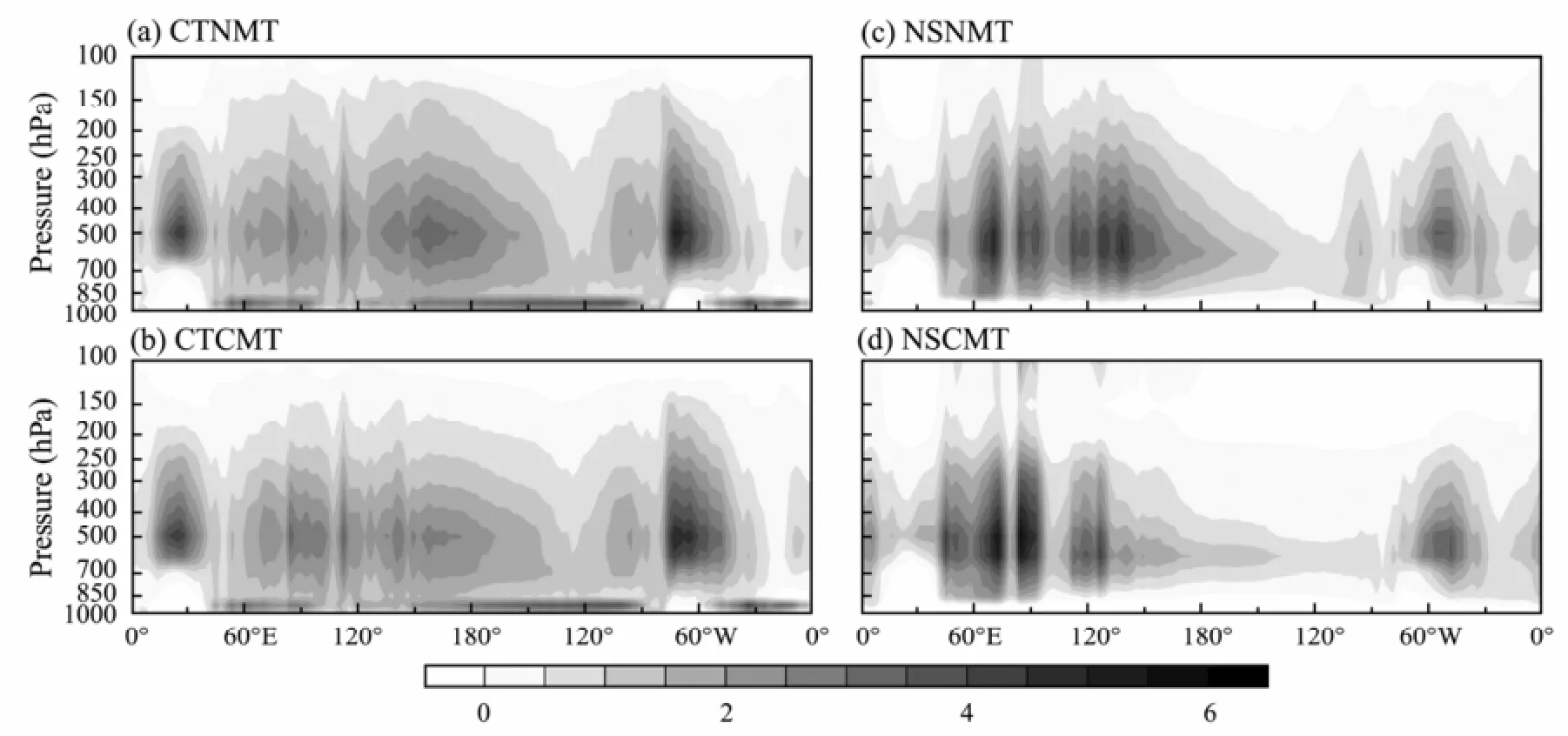
Fig.6 Longitude--pressure distribution of mean total latent heating (K d-1) from (a) control run and (b) no shallow heating run without CMT, and (c), (d) with CMT. All are averaged over 15˚S-15˚N.
Differences between the CMT and no CMT runs in total and the intraseasonal variability of latent heating averaged over the tropical region (15˚S-15˚N) are shown in Fig.7. Simulated total and intraseasonal latent heating in the runs with CMT is weaker than that in the no CMT runs. The two maximum reduction centers are located over the Indian Ocean and western Pacific, respectively. The increase in the variability of latent heating in the no shallow runs (NSCMT) over the 120˚E is related to the enhanced convection over the region between the Maritime Continent and Australia (Fig.4d). However, the reason for the MJO signal almost disappearing in NSCMT needs further investigations. The circulation coupled with deep convection over the tropics is usually of a typical deep, first baroclinic mode extending up to the top of troposphere, with mid-level upward motions, low-level convergence and upper-level divergence in regions of active convection. The effect of CMT is to transport thehorizontal wind momentum within the sub-grid scale vertically between conjunct layers, which reduces the vertical wind shear and the baroclinic structure of convection. Therefore, generally speaking, CMT weakens the baroclinic structure of large-scale organized deep convection in the model, and further weakens precipitation and the associated circulation in the tropics.
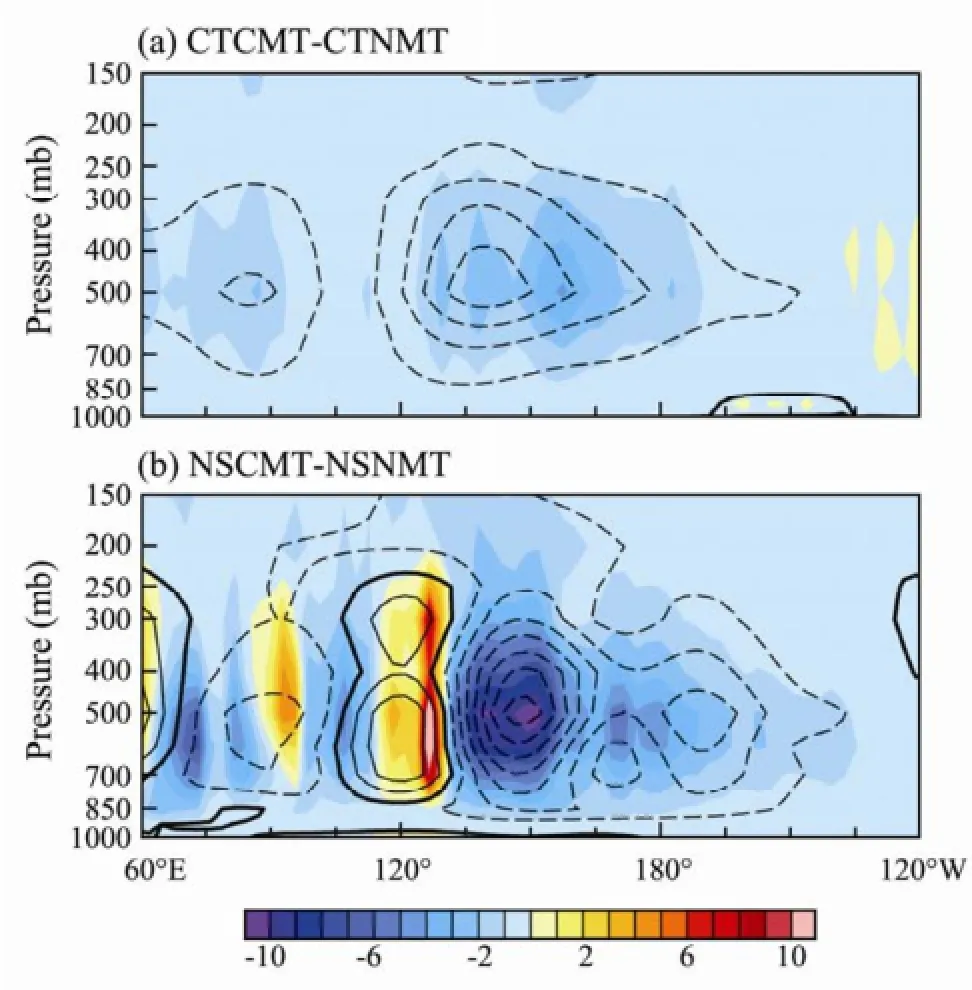
Fig.7 Longitude-pressure distribution of the difference between the total (shaded) and MJO band filtered (contour, interval 0.1) standard deviation of latent heating (K d-1) from (a) control run and (b) no shallow heating run, with and without the CMT. All are averaged over 15˚S-15˚N.
3.4 Moisture Convergence
The importance of moisture, especially low-level moisture above the cloud base, to tropical deep convection has been demonstrated in many previous studies (Tompkins, 2001; Sobel et al., 2004; Holloway and Neelin, 2009). Positive low-level moisture anomalies to the east of the convection center leading active phases of the MJO have been shown in observations/reanalysis data (Johnson et al., 1999; Kemball-Cook et al., 2002; Kiladis et al., 2005) and in model simulations (Thayer-Calder and Randall, 2009; Zhang and Song, 2009).
Vertical structures of latent heating and large-scale horizontal moisture convergence in all simulations along with their associated zonal-vertical circulations are shown in Fig.8. A strong zonal and vertical baroclinic circulation of zonal wavenumber one only clearly exists in NSNMT. The manifestation of the MJO in latent heating and its associated circulation is not shown in the other three simulations. The zonal and vertical scales of the circulation dramatically decrease after CMT is included, and the circulation induced by convection is more localized. The low- and high- level zonal wind shear also reduces in the CMT runs (CTCMT and NSCMT) compared to the no CMT runs (CTNMT and NSNMT).
Low-level moisture convergence is weaker and shallower in the NSCMT run than in the NSNMT run. Positive moisture convergence within the free atmosphere to the east of the convection center disappears in the NSCMT run (Fig.8d) compared to NSNMT run (Fig.8c). Therefore, moisture to the east of the existing convection center isless and insufficient to set the favorable stage for initiation of deep convection. It is consistent with the MJO theory in terms of boundary layer frictional convergence (Wang, 1988; Wang and Rui, 1990). This might be the reason for no eastward propagating intraseasonal oscillation in NSCMT.
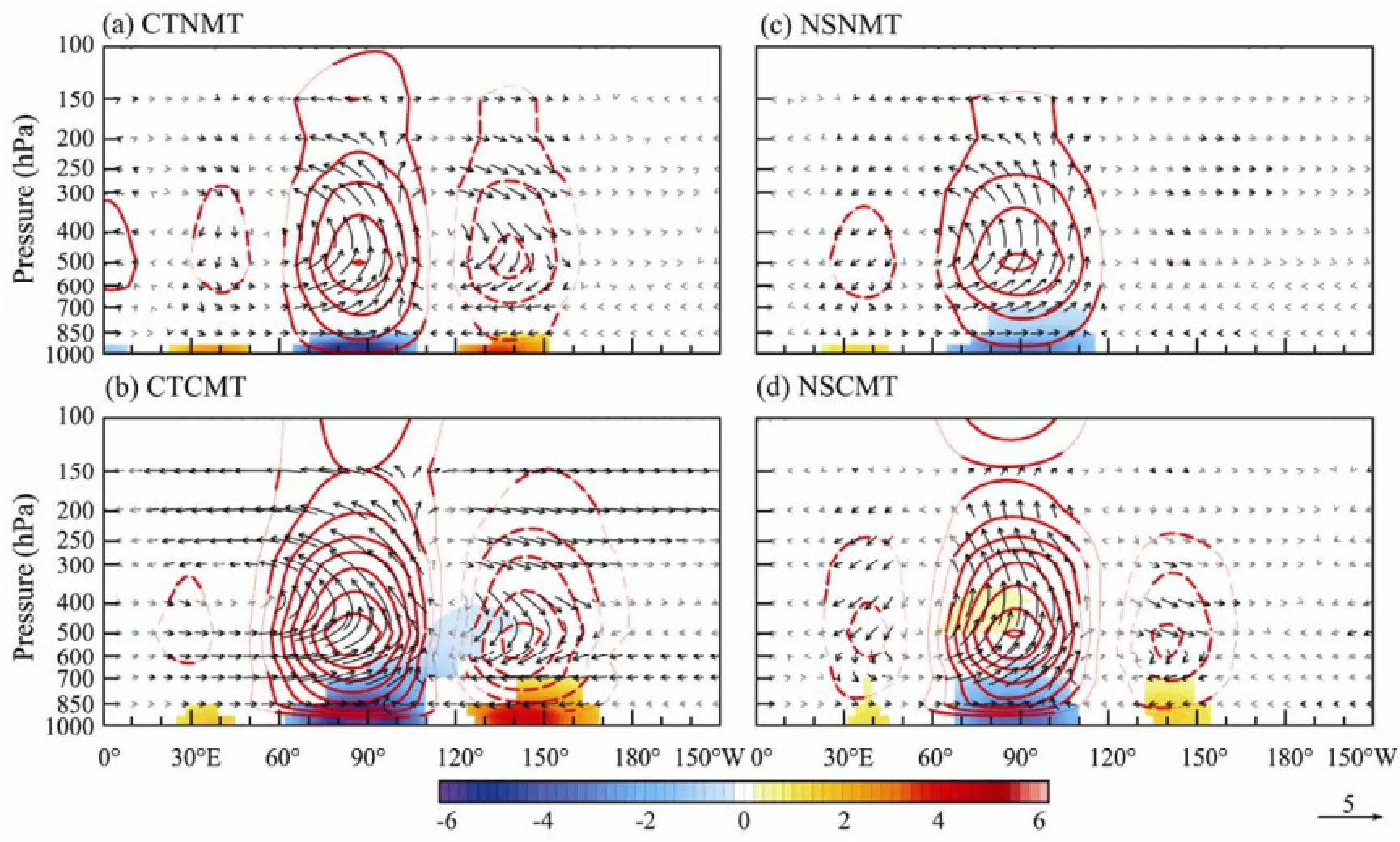
Fig.8 Longitude-pressure distributions of tropical averaged (15°S-15°N) latent heating (contour, interval 0.1Kd-1), moisture divergence (color, 10-5gkg-1s-1) and zonal-vertical wind vectors of the MJO regressed upon MJO EPR at 90°E with time lag 0 day from from the (a) CTNMT, (b) CTCMT, (c) NSNMT, and (d) NSCMT simulations. Dashed contours for negative values and zero contours omitted. Only results passing a significant test with the 90% confidence level or above are plotted for moisture convergence, highlighted by black vector for zonal-vertical wind and thick contours for latent heating.
It is also interesting to point out that moisture convergence in CTCMT is weak but deeper than in CTNMT. Ling et al. (2013) suggested that the latent heating peak in the boundary layer in the CTNMT run tends to confine the moisture within the PBL and prevent it from being transported to the free atmosphere. The influence of CMT on mixing horizontal momentum within the boundary layer can minimize the influence of the heating peak and allow more moisture to be transported into the free atmosphere. However, CMT itself reduces the wind shear within the large-scale convection. Therefore, moisture convergence in the CTCMT run is deeper than in the CTNMT run, but the amplitude of the intraseasonal signal becomes weaker.
4 Summary and Discussion
In this study, the impact of CMT on simulations of the intraseasonal oscillation by SAMIL using Tiedtke cumulus parameterization scheme was investigated. Two sets of experiments were designed to explore the influence of CMT on MJO simulations in models with different MJO simulation capabilities.
When CMT is included in the cumulus parameterization, the amplitude of the intraseasonal oscillation generally becomes weaker not only in the wind field but also in convection regardless of the MJO simulation capability of the model. However, the CMT impact on simulations of the intraseasonal oscillation depends on models’ capability of simulating the MJO. CMT tends to have a stronger impact on MJO simulations in models that simulate the MJO better.
The main impact of CMT is to reduce the wind shear within convection. The transport of zonal wind momentum with the conjunctive layers weakens the baroclinic nature of large-scale organized deep convection. Initiation of deep convection becomes harder and the lifetime of deep convection becomes shorter when CMT is included. If a models cannot simulate deep convection very well, then whether CMT is introduced does not make much difference in its simulation of the intraseasonal oscillation, which is illustrated by the control runs (CTNMT and CTCMT). When CMT is included in a model with strong and frequent deep convection, its impact is much greater. The variability of total and intraseasonal latent heating reduces dramatically in the region where deep convection dominates (Fig.7b).
Including CMT in the cumulus parameterization can further influence the long-term mean of zonal wind and its vertical shear. Zonal wind suffers from easterlies biases at low levels and westerlies biases at upper levels when CMT is included. Such easterlies biases reduce the reality of the simulated tropical intraseasonal oscillation, because the MJO favors low-level westerlies (Inness et al., 2003). The easterly/westerly biases at low/upper levels delay the eastward propagation of the westerly/easterly to the west of the convection center and weaken their amplitudes (Miyakawa et al., 2012). CMT further leads to weaker low-level moisture convergence in the free atmosphere to the east of existing convection centers and prevent the signal of active convection from propagating eastward.
As pointed out in Ling et al. (2009), SAMIL tends to produce stronger intraseasonal oscillation signals than observations. The amplitude of simulated intraseasonal signals is closer to observations when CMT is included, but the eastward propagation signal of the MJO deteriorates. Previous studies also indicated that the a model’s mean state could be improved by introducing CMT into its cumulus paramterization (Tiedtke, 1989). However, other studies pointed out that tuning models for better MJO simulations often degrades the mean climate of the models (Sobel et al., 2010). Therefore, a balance between the simulated mean state and the MJO is necessary. The simple method of removing shallow convection heating in NSCMT and NSNMT also has negative consequences, such as the deteriorated mean state of precipitation (Fig. 4), which might have potential influences on MJO simulations. The sensitive experiments in this study are meant to test the impact of CMT in SAMIL with the Tiedtke scheme and explore CMT impact on MJO simulations. The CMT scheme in the Tiedtke scheme is simple (see section 2.2). Reliable estimates of CMT are difficult to obtain from the momentum budget and relatively few attempts have been made (Carr and Bretherton, 2001; Tung and Yanai, 2002). The development and evaluation of CMT parameterization are always challenging problems and will be so for a long time to come. Qualitatively successful attempts have been made in parameterizing CMT (Kershaw and Gregory 1997; Gregory et al. 1997). In order to fully understand CMT impact on MJO simulations, different CMT schemes and different models are needed.
Acknowledgements
Most of this study was done during the first author’s PhD studies at the Institute of Atmospheric Physics in China. This research is sponsored by the Joint Project of Natural Science Foundation of China and Yunnan Province (U0833602).
Carr, M. T., and Bretherton, C. S., 2001. Convective momentum transport over the tropical Pacific: Budget estimates. Journal of the Atmospheric Sciences,58: 1673-1693.
CLIVAR, 2009. MJO simulation diagnostics. Journal of Climate,22: 3006-3030.
Edwards, J. M., and Slingo, A., 1996. Studies with a flexible new radiation code 1. Choosing a configuration for a largescale model. Quarterly Journal of the Royal Meteorological Society,122: 689-719.
Gregory, D., Kershaw, R., and Inness, P. M., 1997. Parametrization of momentum transport by convection. II: Tests in single-column and general circulation models. Quarterly Journal of the Royal Meteorological Society, 123: 1153-1183.
Hayashi, Y., 1979. A generalized method of resolving transient disturbances into standing and traveling waves by space-time spectral analysis (application to planetary waves). Journal of the Atmospheric Sciences, 36: 1017-1029.
Helfand, H. M., 1979. The effect of cumulus friction on the simulation of the January Hadley circulation by the GLAS model of the general circulation. Journal of the Atmospheric Sciences, 36: 1827-1843.
Hendon, H. H., 2000. Impact of air-sea coupling on the Madden-Julian Oscillation in a general circulation model. Journal of the Atmospheric Sciences, 57: 3939-3952.
Hendon, H. H., Liebmann, B., Newman, M., Glick, J. D., and Schemm, J. E., 2000. Medium-range forecast errors associated with active episodes of the Madden-Julian Oscillation. Monthly Weather Review, 128: 69-86.
Holloway, C. E., and Neelin, J. D., 2009. Moisture vertical structure, column water vapor, and tropical deep convection. Journal of the Atmospheric Sciences, 66: 1665-1683.
Holtslag, A. A. M., and Boville, B. A., 1993. Local versus nonlocal boundary-layer diffusion in a global climate model. Journal of Climate, 6: 1825-1842.
Houze, R. A., 1973. A climatological study of vertical transports by cumulus-scale convection. Journal of the Atmospheric Sciences, 30: 1112-1123.
Inness, P. M., and Gregory, D., 1997. Aspects of the intraseasonal oscillation simulated by the Hadley Centre Atmosphere Model. Climate Dynamics, 13: 441-458.
Inness, P. M., Slingo, J. M., Guilyardi, E., and Cole, J., 2003. Simulation of the Madden-Julian Oscillation in a coupled general circulation model. Part II: The role of the basic state. Journal of Climate, 16: 365-382.
Jia, X. L., Li, C. Y., and Ling, J., 2009. Impacts of cumulus parameterization and resolution on the MJO simulation. Journal of Tropical Meteorology, 15: 106-110.
Jia, X. L., Li, C. Y., Ling, J., and Zhang, C. D., 2008. Impacts of a GCM’s resolution on MJO simulation. Advances in Atmospheric Sciences, 25: 139-156.
Jia, X. L., Li, C. Y., Zhou, N. F., and Ling, J., 2010. The MJO in an AGCM with three different cumulus parameterization schemes. Dynamics of Atmospheres and Oceans, 49: 141-163.
Johnson, R. H., Rickenbach, T. M., Rutledge, S. A., Ciesielski, P. E., and Schubert, W. H., 1999. Trimodal characteristics of tropical convection. Journal of Climate, 12: 2397-2418.
Kalnay, E., 1996. The NCEP/NCAR 40-year reanalysis project. Bulletin of the American Mathematical Society, 77: 437-471.
Kemball-Cook, S., Wang, B., and Fu, X. H., 2002. Simulation of the intraseasonal oscillation in the ECHAM-4 model: The impact of coupling with an ocean model. Journal of the Atmospheric Sciences, 59: 1433-1453.
Kershaw, R., and Gregory, D., 1997. Parametrization of momentum transport by convection. I: Theory and cloud modelling results. Quarterly Journal of the Royal Meteorological Society, 123: 1133-1151.
Kiladis, G. N., Straub, K. H., and Haertel, P. T., 2005. Zonal and vertical structure of the Madden-Julian Oscillation. Journal of the Atmospheric Sciences, 62: 2790-2809.
Kim, D., 2009. Application of MJO simulation diagnostics to climate models. Journal of Climate, 22: 6413- 6436.
Lau, K. M., and Waliser, D. E., 2012. Intraseasonal Variability in the Atmosphere-Ocean Climate System. 2nd edition. Springer, 1-35.
Li, C. Y., and Zhang, M., 1984. Numerical simulation study–Role of the cumulus momentum transport. Acta Meteorologica Sinica, 42 (4): 466-474 (in Chinese).
Li, C. Y., Jia, X. L., Ling, J., Zhou, W., and Zhang, C. D., 2009. Sensitivity of MJO simulations to diabatic heating profiles. Climate Dynamics, 32: 167-187.
Li, R. C. Y., Zhou, W., Chan, J. C. L., and Huang, P., 2012. Asymmetric modulation of Western North Pacific Cyclogenesis by the Madden-Julian Oscillation under ENSO conditions. Journal of Climate, 25: 5374-5385.
Lin, J. L., 2006. Tropical intraseasonal variability in 14 IPCC AR4 climate models. Part I: Convective signals. Journal of Climate, 19: 2665-2690.
Ling, J., and Zhang, C. D., 2011. Structural evolution in heating profiles of the MJO in global reanalyses and TRMM retrievals. Journal of Climate, 24: 825-842.
Ling, J., and Zhang, C., 2012. Diabatic heating profiles in recent global reanalyses. Journal of Climate, 26: 3307- 3325.
Ling, J., Li, C. Y., and Jia, X. L., 2009. Impacts of cumulus momentum transport on MJO simulation. Advances in Atmospheric Sciences, 26: 864-876.
Ling, J., Li, C., Zhou, W., Jia, X., and Zhang, C., 2013. Effect of boundary layer latent heating on MJO simulations. Advances in Atmospheric Sciences, 30: 101-115.
Madden, R. A., and Julian, P. R., 1971. Detection of a 40–50 day oscillation in zonal wind in tropical Pacific. Journal of the Atmospheric Sciences, 28: 702.
Madden, R. A., and Julian, P. R., 1972. Description of globalscale circulation cells in tropics with a 40–50 day period. Journal of the Atmospheric Sciences, 29: 1109.
Maloney, E. D., and Hartmann, D. L., 2001. The sensitivity of intraseasonal variability in the NCAR CCM3 to changes in convective parameterization. Journal of Climate, 14: 2015-2034.
Miyakawa, T., Takayabu, Y. N., Nasuno, T., Miura, H., Satoh, M., and Moncrieff, M. W., 2012. Convective momentum transport by rainbands within a Madden-Julian Oscillation in a global nonhydrostatic model with explicit deep convective processes. Part I: Methodology and general results. Journal of the Atmospheric Sciences, 69: 1317-1338.
Nordeng, T. E., 1994. Extended versions of the convective parametrization scheme at ECMWF and their impact on the mean and transient activity of the model in the Tropics. ECMWF Research Department, Technical Memorandum, No. 206, 1-14.
Ose, T., Tokioka, T., and Yamazaki, K., 1989. Hadley circulations and penetrative cumulus convection. Journal of the Meteorological Society of Japan, 67: 605-619.
Paegle, J. N., Byerle, L. A., and Mo, K. C., 2000. Intraseasonal modulation of South American summer precipitation. Monthly Weather Review, 128: 837-850.
Schneider, E. K., and Lindzen, R. S., 1976. A discussion of the parameterization of momentum exchange by cumulus convection. Journal of Geophysical Research, 81: 3158-3160.
Sellers, P. J., Mintz, Y., Sud, Y. C., and Dalcher, A., 1986. A simple biosphere model (SIB) for use within general circulation models. Journal of the Atmospheric Sciences, 43: 505-531.
Simmonds, I., 1985. Analysis of the spinup of a generalcirculation model. Journal of Geophysical Research – Atmospheric, 90: 5637-5660.
Slingo, J. M., 1980. A cloud parametrization scheme derived from gate data for use with a numerical-model. QuarterlyJournal of the Royal Meteorological Society, 106: 747-770.
Slingo, J. M., 1987. The development and verification of a cloud prediction scheme for the ecmwf model. Quarterly Journal of the Royal Meteorological Society, 113: 899-927.
Slingo, J. M., 1996. Intraseasonal oscillations in 15 atmospheric general circulation models: Results from an AMIP diagnostic subproject. Climate Dynamics, 12: 325-357.
Sobel, A. H., Yuter, S. E., Bretherton, C. S., and Kiladis, G. N., 2004. Large-scale meteorology and deep convection during TRMM KWAJEX. Monthly Weather Review, 132: 422-444.
Song, X. L., 2005. The evaluation analysis of two kinds of mass-flux cumulus parameterization in climate simulation. PhD thesis, Institute of Atmospheric Physics, Chinese Academy of Sciences, 158pp (in Chinese).
Stevens, D. E., Lindzen, R. S., and Shapiro, L. J., 1977. A new model of tropical waves incorporating momentum mixing by cumulus convection. Dynamics of Atmospheres and Oceans, 1: 365-425.
Thayer-Calder, K., and Randall, D. A., 2009. The role of convective moistening in the Madden-Julian Oscillation. Journal of the Atmospheric Sciences, 66: 3297-3312.
Tiedtke, M., 1989. A comprehensive mass flux scheme for cumulus parameterization in large-scale models. Monthly Weather Review, 117: 1779-1800.
Tompkins, A. M., 2001. Organization of tropical convection in low vertical wind shears: The role of water vapor. Journal of the Atmospheric Sciences, 58: 529-545.
Tung, W. W., and Yanai, M., 2002. Convective momentum transport observed during the TOGA COARE IOP. Part I: General features. Journal of the Atmospheric Sciences, 59: 1857-1871.
Waliser, D. E., Lau, K. M., and Kim, J. H., 1999. The influence of coupled sea surface temperatures on the Madden-Julian Oscillation: A model perturbation experiment. Journal of the Atmospheric Sciences, 56: 333-358.
Wang, B., 1988. Dynamics of tropical low-frequency waves–An analysis of the Moist Kelvin wave. Journal of the Atmospheric Sciences, 45: 2051-2065.
Wang, B., and Rui, H., 1990. Synoptic climatology of transient tropical intraseasonal convection anomalies–1975–1985. Meteorology and Atmospheric Physics, 44: 43-61.
Wang, W. Q., and Schlesinger, M. E., 1999. The dependence on convection parameterization of the tropical intraseasonal oscillation simulated by the UIUC 11-layer atmospheric GCM. Journal of Climate, 12: 1423-1457.
Wang, X., Wang, D., Zhou, W., and Li, C., 2012. Interdecadal modulation of the influence of La Niña events on mei-yu rainfall over the Yangtze River valley. Advances in Atmospheric Sciences, 29: 157-168.
Wu, G., Liu, H., Zhao, Y., and Li, W., 1996. A nine-layer atmospheric general circulation model and its performance. Advances in Atmospheric Sciences, 13: 1-18.
Xue, Y., Sellers, P. J., Kinter, J. L., and Shukla, J., 1991. A simplified biosphere model for global climate studies. Journal of Climate, 4: 345-364.
Zhang, C. D., 2005. Madden-Julian Oscillation. Reviews of Geophysics, 43 (2), DOI: 10.1029/2004RG000158.
Zhang, C. D., 2010. MJO signals in latent heating: Results from TRMM retrievals. Journal of the Atmospheric Sciences, 67: 3488-3508.
Zhang, C. D., and Gottschalck, J., 2002. SST anomalies of ENSO and the Madden-Julian Oscillation in the equatorial Pacific. Journal of Climate, 15: 2429-2445.
Zhang, C. D., Dong, M., Gualdi, S., Hendon, H. H., Maloney, E. D., Marshall, A., Sperber, K. R., and Wang, W. Q., 2006. Simulations of the Madden-Julian Oscillation in four pairs of coupled and uncoupled global models. Climate Dynamics, 27: 573-592.
Zhang, C., and Dong, M., 2004. Seasonality in the Madden-Julian Oscillation. Journal of Climate, 17: 3169-3180.
Zhang, G. J., and Mcfarlane, N. A., 1995. Sensitivity of climate simulations to the parameterization of cumulus convection in the Canadian Climate Center general-circulation model. Atmosphere Ocean, 33: 407-446.
Zhang, G. J., and Song, X. L., 2009. Interaction of deep and shallow convection is key to Madden-Julian Oscillation simulation. Geophysical Research Letters, 36 (9), DOI: 10. 1029/2009GL037340.
Zhou, W., and Chan, J. C. L., 2005. Intraseasonal oscillations and the South China Sea summer monsoon onset. International Journal of Climatology, 25: 1585-1609.
(Edited by Xie Jun)
(Received February 4, 2013; revised February 18, 2013; accepted May 13, 2014)
© Ocean University of China, Science Press and Springer-Verlag Berlin Heidelberg 2014
* Corresponding author. E-mail: lingjian@lasg.iap.ac.cn
 Journal of Ocean University of China2014年5期
Journal of Ocean University of China2014年5期
- Journal of Ocean University of China的其它文章
- Identification of Fucans from Four Species of Sea Cucumber by High Temperature1H NMR
- The Appearance of Ulva laetevirens (Ulvophyceae, Chlorophyta) in the Northeast Coast of the United States of America
- Metabolic and Phylogenetic Profile of Bacterial Community in Guishan Coastal Water (Pearl River Estuary),South China Sea
- Distribution and Source of Main Contaminants in Surface Sediments of Tidal Flats in the Northern Shandong Province
- Analgesis and Wound Healing Effect of Chitosan and Carboxymethyl Chitosan on Scalded Rats
- Histological Observation of Germ Cell Development and Discovery of Spermatophores in Ovoviviparous Black Rockfish (Sebastes schlegeli Hilgendorf) in Reproductive Season
