Goal programming approach for sustainable forest management (case study in Iranian Caspian forests)
Soleiman Mohammadi Limaei • Maryam Seddigh Kouhi Teymour Rostami Sharaji
Introduction
The forestry sector is well positioned to provide worldwide leadership in sustainable development. The forestry community is accustomed to long-term perspectives; it is knowledgeable about responses of forest ecosystems to natural and human disturbances; it is comfortable with the sustained yield principle; and, in a few instances, it has attempted to practice multiple-use and integrated-use of forests (FAO 2013).
Sustainable forest management is the management of forests, based on the principles of sustainable development. Sustainable forest management seeks to achieve social, economic and environmental goals.
Traditional forest planning sought achievement of economic goals such as maximizing Net Present Value (NPV) through timber harvest or enhancing environmental protection. Less attention was given to multipurpose goals because, in many cases, these goals conflicted with each other and it seemed impossible to accomplish them simultaneously. In the face of diminishing forest resources but increasing management capacities, forest management is shifting toward a multipurpose approach from which optimal results can be obtained from minimal resources. There are three main goals in forest management: (1) Economic goal: Related to harvest of timber and non timber resources; (2) Social goal: Including satisfying social needs such as maximizing employment, satisfying needs of forest residents and people living in the forest neighborhood; (3) Environmental goal: Including maximizing of carbon sequestration and protection of soil and water resources.
During the last two decades, the importance of sustainable forestry has increased. The concept of “sustainable” means that, forest resources should be used today in ways that do not compromise their use in future. The concept of forestry has shifted from sustainable product to sustainable ecology, sustainable economy and society. In fact as time elapse, the importance of products and services related that are related to forests increases (Nouri et al. 2010). Today managing the sustainability of forests is considered as the contribution of the forestry in sustainable development (Higman et al. 2005).
Improving living condition of animals dependent to forest ecosystem, as well as conserving variety of forest stands are among the main goals of modern forestry (Pommerening 2002). It also means, managing and using forest resources in a way that biological diversity, production and the possibility of potential production of forests according to its ecological capacities would be saved and no harm would be threading other ecosystems (Bernasconi 1996).
One of the mathematical techniques that could handle a multipurpose problem is Goal Programming (GP). GP is a special case of linear programming (Kangas et al. 2008). It was first described by Charnes and Cooper (1961). A forestry application of GP was first presented by Field (1973). After that, several applications of GP to forest management planning was presented (D´ıaz-Balteiro and Romero 2003). Mendoza (1987) provided an overview of GP formulations and extensions with special reference to forest planning. Tamiz et al. (1998) provided a more general overview of GP elaborations and applications. Some crucial problems of standard linear programming can be avoided using GP model. However, the GP problem is solved similarly as in standard linear programming.
Bettinger et al. (2009) mentioned the application of GP model to the following cases:
· Determination of present and future production from the land, as well as the demand for the different products.
· Estimation of physical capacity of the land to produce the various products.
· Analyze the complementary and competitive relationships among the goals.
· Determination the feasible set of desirable goals.
· Express the goals as a single objective function, and design the problem formulation using the appropriate constraints.
Gomez et al. (2006) used GP method to create balance among the diameter classes in Cuba’s forest, the forest was extremely harmed due to natural disasters and harvesting.
Samghabadi et al. (2004) Developed a mathematical model for sustainable forest development by strategic land use planning in Ramsar watershed in north of Iran. At their research, GP is used for modeling. Their results indicated that it is possible to reach the optimum goals such as maximization of carbon sequestration, NPV of income, stand volume, employment and minimization of soil erosion. We undertook a research project to develop a model for sustainable forestry in Iran based on the concept of sustainability defined by Report of the World Commission on Environment and Development (WCED) (1987). Therefore, GP model was applied to determinate the optimum standing timber or volume based on multi criteria decision making in Shafaroud forest, Iranian Caspian forests, and north of Iran.
Materials and methods
Study area
We collected data from district number 11 at Shafaroud forest in north of Iran. These forests are located in mountainous area and its altitude ranges from 500 to 1650 m. This district consists of 45 compartments and its cover 2202.9 ha. Of this, 1887.1 ha are suitable for harvesting, 98.5 ha are protected forests, 143.8 ha are bare land, 0.8 ha is agricultural and residential area, and 72.7 ha are covered by roads. These forests are uneven-aged and the main species are: beech (Fagus orientalis), hornbeam (Carpinus sp), oak (Quercus sp), alder (Alnus sp) and etc. This forest is managed under selection system (Fig. 1).

Fig. 1: Iranian forests map (FAO 1999, Global Forest Cover map) and the study area (Shafaroud forest).
The collected data
We collected data including volume, growth, sequestrated carbon, wood price at forest roadside, logging and wood transportation costs, and number of required labor to manage the forest. We used questionnaires in order to weight the different goals in multipurpose forest management.
We obtained volume and growth data from previous research (Bonyad 2005), (Table 1). We obtained sequestrated carbon data using allometric equations (Kabiri Koupaei 2009).

Table 1: Volume and growth of different species at Shafaroud uneven-aged forest, north of Iran (Bonyad 2005)
Growth function
We assumed that annual growth is a function (f) of volume (Mohammadi Limaei 2006):

where, G is growth (m3·ha-1·a-1), V is stock level (m3·ha-1). We used regression analysis to estimate the growth function.
Carbon sequestration
We used the allometric method to determine the above ground stand sequestrated carbon. At this method, first of all we determined the biomass of stand, then we considered 50% of dry stand weight as the amount of sequestrated carbon (Snowdon et al. 2002). The most commonly used mathematical model for biomass studies is Y= aDb, where, a and b are the scaling coefficients, Y is the total above ground tree dry biomass and D is the diameter at breast height. Value a and b reported to vary with species, stand age, site quality, climate, and stocking of stands (Baskerville 1965). According to the above mentioned method, we estimated the amount of sequestrated carbon using the allometric functions determined by Kabiri Koupaei (2009).
Expected mean price
We derived the stumpage price data from actual timber, roundwood, fire and pulpwood prices at forest roadside minus the variable harvesting costs. Then we adjusted it by consumer price index (CPI) for the base year 2004. We used regression analysis to predict the price processes. We used the estimated parameters from regression analysis to determine the expected mean price using the following equation (Mohammadi Limaei 2011).

where, Peqis the expected mean price, α and β are the estimated parameters.
Goal programming (GP) model
A GP model, similar to the LP model consist an objective function and constraints. It can be thought of as an extension or generalization of LP to handle multiple objectives. Each of these objectives is given a goal or target value to be achieved. Unwanted deviations from this set of target values are then minimized in an achievement function. In GP, all the objectives are handled in the same manner: they are expressed by goal constraints. A goal constraint includes goal variables that measure the amount by which the contribution of all activities to the goal in question falls short or exceeds the goal level (i.e. the right hand side of the constraint). The objective function of a GP problem is to minimize the sum of the (weighted) deviations from all target levels associated with the management goals. When goal variables are included in a constraint, the problem of infeasibility linked to the constraint is avoided (Kangas et al. 2008). The following function is the GP objective function:

The deviations can be weighted according to their importance, in the objective functionis the weight given to each unit of underachievement deviation ();is the weight given to each unit of overachievement deviation (). The weights can be interpreted to have two separate roles in the problem. As scaling factors, weightsandreduce deviations expressed in different measurement units to a common unit of measurement. As importance weights, they describe the relative importance’s of the goal variables. Because of these intermingling roles, the interpretation of weights as relative importance of goals, respectively, is not unambiguous (Kangas et al. 2008).
The weights fulfill two purposes. They express all deviations from goals in a common unit of measurement, and they reflect the relative importance of each goal (Buongiorno and Gilless 2003). Deviations that concern the decision makers most get the larger weights relative to the others. Deviations that are of no concern or are looked at favorably may be omitted from the objective function altogether (Buongiorno and Gilless 2003). The choice of weights for objective function (3) can be simplified by considering the relative, rather than the absolute, deviations with respect to goals. The new expression of the objective function is then:


where, Xjis the jth activity (decision) variable. aijis the (constant) contribution to goal i per unit of activity j The giis a constant measuring the target of goal i, of which there are G. As long as bothandare present in a goal constraint, no infeasibility may result from that constraint. The goal variables always fill the gap between the goal level and what is actually achieved. Other constraints may be present, of the usual LP variety; that is (Buongiorno and Gilless 2003):

Formulating of GP model
We used functions 3 to 6 to determine the optimal standing timber in the study area. We determined the constraints and objective function of GP model as below:
Constraint functions
First of all, we determined the following functions as the constraints:

Equation 7 is a constraint that shows the minimum total feasible volume (m3·ha-1) that obtained from questionnaires. Where X1is volume of beech, X2is volume of hornbeam, X3is volume of oak, X4is volume of alder and X5is volume of the other species.

Equation 8 is minimum feasible volume of beech. It should be equal or more than 251 m3·ha-1that determined from questionnaires.
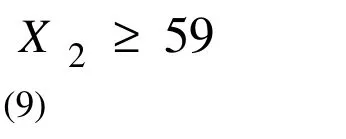
Equation 9 is minimum feasible volume of hornbeam. It should be equal or more than 59 m3·ha-1that determined from questionnaires.

Equation 10 is minimum feasible volume of oak. It should be equal or more than 73 m3·ha-1that determined from questionnaires.

Equation 11 is minimum feasible volume of alder. It should be equal or more than 41 m3·ha-1that determined from questionnaires.

Equation 12 is minimum feasible volume of other species. It should be equal or more than 41 m3·ha-1that determined from questionnaires.

Equation 13 is minimum feasible sequestrated carbon (t·ha-1). The coefficients for decision variables (1X to X5) are the sequestrated carbon that calculated for each species.

Equation 14 is minimum feasible growth per hectare that calculated by volume per hectare. The coefficients for1X to X5are growth per hectare that calculated for each species.
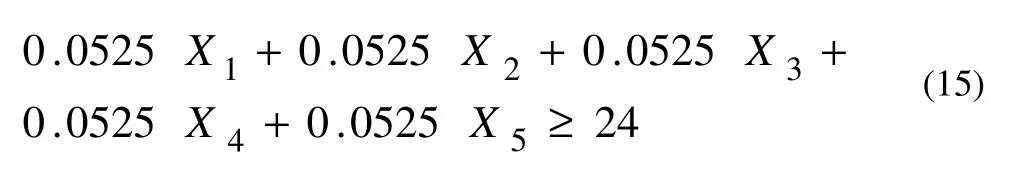
Equation 15 is the minimum feasible personnel or labor based on forest management plan (Iranian Forests, Rangeland and Watershed Management Organization 1999). The coefficients for1X to X5are the amount of labor to manage one cubic meter of stock and it is assumed to be equal for all species.
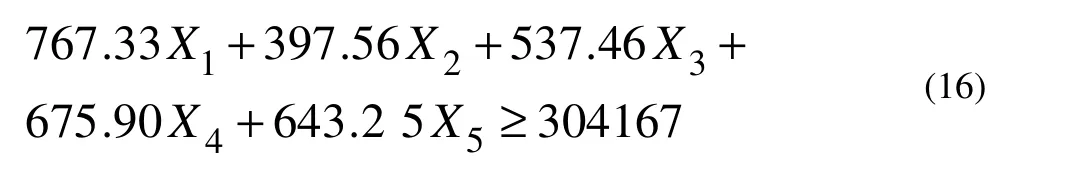
Equation 16 is minimum acceptable NPV of stock (10000 Iranian Rials) that is determined based on stumpage price, volume, growth and rate of interest. The coefficients for1X to X5are the NPV calculated for each species (10000 Iranian Rials).
We determined the negative or positive deviation from goal based on the constraints properties. If the initial constraint or inequality is greater than a quantity, then the negative deviation should be included in the equation. This negative deviation should be written on the left hand side of the equation and the inequality will be changed to equality. In case the initial constraint is less than a quantity, then positive deviation should be subtracted from left hand side of the equation. On the other hand, the signsorcan be added to relations 7 to 16 in the different above mentioned cases. According to the properties of the constraints at this study, we did not have any positive deviation from the goal. Consequently, the following new equations are determined: where, DVTis negative deviation of total volume, DFis negative deviation of beech volume, DCARis negative deviation of hornbeam volume, DQis negative deviation of oak volume, DAis negative deviation of alder volume, DOis negative deviation of other species volume, DCis negative deviation of sequestrated carbon, DGis negative deviation of growth per hectare,is negative deviation of labor, DNPVis negative deviation of NPV of volume.

Objective function
The aim of objective function was to minimize the unfavorable deviation from the goal. Therefore, the following function was determined:


Finally we solved the GP model consisting of objective function and constraints using LINGO software.
Results
Growth function
Results of regression analysis showed that the logarithmic equation is the best model to predict the growth function based on the collected data. The growth equations are shown in Table 2. It should be noted that in all of the equations at Table 2, Y is average growth (m3·ha-1·a-1) X is volume (m3·ha-1). All of the functions were significant at significance level of 0.05.

Table 2: Growth functions of different species.
Expected mean price
Expected mean prices of different species are determined using Eq. (2) and the estimated parameters of regression analysis (Table 3).

Table 3: Estimated parameters based on regression analysis for stumpage price and expected mean price of different species.
Carbon sequestration
We determined the relation between sequestrated carbon (t·ha-1) (Y) and volume (m3·ha-1) (X) based on the allometric function for different species (Table 4). All of the functions were significant at the significance level of 0.05 and R2=0.99.

Table 4: Carbon sequestration functions of different species.
Goal programming model
The results of GP model is shown in Table 5 that solved by LINGO software. It indicates that optimum volume of beech is 250.25 m3·ha-1and its negative deviations from the goal is 0.75 m3·ha-1.

Table 5: Results of goal programming model solved in LINGO software
Optimum volume of hornbeam, oak, alder and the other species are 59 m3·ha-1, 73 m3·ha-1, 41 m3·ha-1and 32 m3·ha-1, respectively. There negative deviations are zero. It means they exactly meet the goal.
Finally we calculated the total optimum volume based on the obtained result that is 455.25 m3·ha-1.
Results also show that there were no slack or surplus for all the constraints. But the constraints such as carbon sequestration, labor, and growth exactly meet the goals without any deviations. Results also show that the constraints such as NPV, beech volume and total volume don’t meet the goals without adding the deviations. Therefore, the negative deviation of NPV is 1150.710 (10000 Iranian Rials). The negative deviation of total volume and beech volume are 1.75 m3·ha-1and 0.75 m3·ha-1), respectively.
Conclusions
This research was carried out in order to determine the optimal volume based on different factors such as sequestrated carbon, minimum acceptable labor, growth, NPV of stand. D´ıaz-Balteiro and Romero (2003) used GP in order to determine the optimal forest management concerning carbon sequestration in Spain. The goal at their model was maximizing NPV, harvested volume control, area control at different ages and final volume. They used 8 scenarios to solve the model that different goals vary at different scenarios. Hence, there is some similarity between the results of their model and this research.
Gomes et al. (2006) used GP model for timber harvest scheduling problem in order to obtain a balanced age class distribution of a forest plantation in Cuba. This forest was destroyed by natural disaster and over exploitation. The main goal was to organize and regulate the forest. This involves a significant change from its current distribution by ages to obtain a more even-aged structure over a planning horizon of 25 years which coincides with the rotation age. The proposed model aims to archive the new distribution while bearing in mind the economic aspects of the forest as well as other factors. They obtained several solutions that provided a regulated forest while respecting the economic and other targets of the decision-makers.
Samghabodi et al. (2004) developed a GP model by strategic landuse planning for a watershed in north of Iran. They used multi-criteria optimization for modeling. The objective function was maximization of carbon sequestration, NPV of income, stand volume, maximizing employment and minimization of soil erosion. They used Lp-norm to aggregate the objectives. There is some similarity between the results of their research and this paper, but the environmental factor was different at these two researches. They used soil erosion as an environmental factor whereas at this research carbon sequestration is used as an environmental factor for GP modeling.
Dı´az-Balteiro and Romero (2003) used GP model for forest management when carbon capture is considered in Spanish forest‘‘Pinar de Navafrı´a’’ located in the mountains of ‘‘Sierra de Guadarrama’’ near Madrid. The results reveal difficulty in ob-taining from an economic and forestry viewpoint good harvest schedules compatible with high levels of carbon captured.
Chang et al. (2009) used the multi-criteria to solve a real-world, revitalization strategies project selection problem for the historic Alishan Forest Railway in Taiwan by using fuzzy Delphi, analytic network process, and zero-one goal programming. They suggested an improved methodology, one that uses an integrated approach and reflects the interdependencies between the evaluation criteria and candidate projects. The management of the Alishan Forest Railway has implemented the processing system proposed by their research and suggested to the government the best alternative strategies.
However, GP model is one of the techniques that could handle the multipurpose management, as it was discussed before. This technique applied to solve forest management problems with different goals and criteria at different countries. The decision makers can use this method for sustainable forest management to consider economics, environmental and social aspects of forest management.
Baskerville GL. 1965. Estimation of dry weight of tree components and total standing crop in conifer stands. Ecology, 46: 867–869.
Bernasconi A. 1996. From sustainability to sustainable systems: Forestry planning as the basis of sustainable forest management. Swiss Journal of Forestry, 76: 176. (In German).
Bettinger P, Boston K, Siry J, Grebner DL. 2009. Forest Management and Planning. USA: Academic Press, p. 360.
Bonyad AE. 2005. Measurement and statically analysis of forest growth at three altitude classes in Shafaroud forests. Report of Research Plan (Working paper). Iran: University of Guilan, pp. 30–65.
Buongiorno J, Gilless JK. 2003. Decision Methods for Forest Resource Management. USA: Academic Press, p. 439.
Chang YH, Weyb WM, Tsenga HY. 2009. Using ANP priorities with goal programming for revitalization strategies in historic transport: A case study of the Alishan Forest Railway. Expert Systems with Applications, 36 (4): 8682–8690
D´ıaz-Balteiro L, Romero C. 2003. Forest management optimization models when carbon captured is considered. A goal programming approach. Forest Ecology and Management, 174: 447–457.
FAO. 1999. FRA 2000, Global Forest Cover map. Rome, Italy: FAO, Forestry Department, Working paper, No 50. p. 29.
FAO. 2013. Sustainable development of forests. Available at: http://www.fao.org/docrep/u6010e/u6010e03.htm.
Field DB. 1973. Goal programming for forest management. Forest Science, 19: 125–135.
Gomez T, Hernandez M, León MA, Caballero R. 2006. A forest planning problem solved via a linear fractional goal programming model, Forest Ecology and Management, 227: 79–88.
Higman S, Mayers J, Bass S, Judd N, Nussbaum R. 2005. The Sustainable Forestry Handbook. London, UK: Earthscan press, p. 332.
Iranian Forests, Rangeland and Watershed Management Organization. 1999. Shafaroud Forest Management Plan Booklet. Tehran, Iran: FRWMO, p. 180.
Kabiri Koupaei K. 2009. Comparison of Carbon Sequestration and its Spatial Pattern in the Above Ground Woody Compartment of a Pure and Mixed Beech Forest (A case study of Gorazbon Forest, North of Iran). PhD Thesis. Iran: Faculty of Natural Resources, University of Tehran, Karaj, Iran.
Kangas A, Kangas J, Kurttila M. 2008. Decision support for forest management. Series: Managing Forest Ecosystems, Vol. 16. Dordrecht, Netherlands: Springer Publication, p. 238.
Mohammadi Limaei S. 2006. Economically Optimal Values and Decisions in Iranian Forest Management. Doctoral thesis. Umea, Sweden: Dept. of Forest Economics, Swedish University of Agricultural Sciences (SLU), Acta Universitatis Agriculturae Sueciae, p. 110.
Mohammadi Limaei S. 2011. Economics Optimization of Forest Management. Germany: LAP LAMBERT Academic Publication, p.140.
Nouri Z, Feghhi J, Zahedi Amiri Gh, Zobeiri M, Rahmani R. 2010. The study of shrub and tree species diversity and its application in forest planning (case study: Patom District, Kheyroud Forest). Journal of Forest and Wood Products, 63(2): 201–214.
Pommerening A. 2002. Approaches to quantifying forest structures. Forestry, 75 (3): 305–324.
Samghabodi AS, Memariani A, Amani A. 2004. Forest planning with use mathematical model. Pajouhesh & Sazandegi, 63: 23–34. (In Persian).
Snowdon P, Raison J, Keith H, Riston P, Grierson P, Adams M, Montagu K, Bi HQ, Burrows W, Eamus D. 2002. Protocol for sampling tree and stand biomass. Australia: Australian Greenhouse Office, p. 66.
Tamiz M, Jones D, Romero C. 1998. Goal programming for decision making: an overview of the current state-of-the-art. European Journal of Operational Research, 111: 569–581.
WCED. 1987. Report of the World Commission on Environment and Development, General Assembly Resolution 42/187, 11 December 1987. Available at: http://www.un.org/documents/ga/res/42/ares42-187.htm.
 Journal of Forestry Research2014年2期
Journal of Forestry Research2014年2期
- Journal of Forestry Research的其它文章
- Compatibility and complementarity of indigenous and scientific knowledge of wild plants in the highlands of southwest Saudi Arabia
- Fragmentation patterns and systematic transitions of the forested landscape in the upper Amazon region, Ecuador 1990−2008
- Carbon sequestration in Chir-Pine (Pinus roxburghii Sarg.) forests under various disturbance levels in Kumaun Central Himalaya
- Genetic variability and divergence studies in pod and seed traits of Pongamia pinnata (L.) Pierre., accessions in Bay Islands
- Spatial distributions of tropical tree species in northern Vietnam under environmentally variable site conditions
- Effect of seed mass on emergence and seedling development in Pterocarpus marsupium Roxb.
