水轮发电机的电自然频率与低负荷振荡计算
张秀丽
(葛洲坝集团第二工程有限公司,成都,610091)
1 概述
在发电机用作调相运行或蓄能机组的电动机运行状态,由于水力机械是处于无水状态或者是接近满负荷运行,因而不存在低负荷振荡问题。发电机在较高负荷运行时,水力脉动显著减小,不足为害。只有数量较小的双频脉动频率在低速机组中有时接近发电机的电自然频率时,才会造成小量的出力脉动。
计算目的:依据压力钢管拼装,及压力钢管段调保计算值,详细计算压力钢管各段的固有频率,以判定是否与管内高压水流冲击叶片形成的压力波及尾水管内旋转涡流引起的钢管振动频率相耦合。
2 水轮机尾水管脉动频率计算
水轮机尾水管脉动频率与水轮机和尾水管的设计参数密切相关,并且随负荷变化而变化,但一般水轮机在满负荷的50%以下低负荷情况下,其脉动频率可按下式估算:
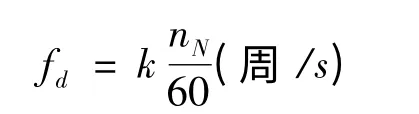
其中,nN为额定转速(RPM);k为系数,在0.25~0.3范围,常为0.28。
例如,nN为180RPM及360RPM,则fd约为0.84及1.68,而大型发电机的电自然频率常在0.8~1.6范围,因而机组转速在180RPM~360RPM范围时会产生低负荷出力振荡。
水轮发电机的自然频率计算:
其中,Prpu为发电机功率角曲线上斜率的标么值,
Pr为发电机功率角曲线上的斜率,单位为千瓦/电弧度。
空载时:
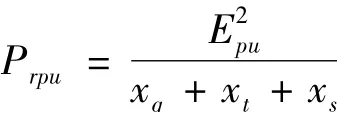
其中,Epu为母线电压标么值,通常为1;xq为发电机横轴同步电抗的标么值;xt为发电机出线端变压器电抗的标么值(以发电机KVA为基础)。
3 钢管的自然振动频率计算

式中:fμ——圆形壳体的自然振动频率(次/s);
r——压力钢管的半径,r=150cm;
Eg——钢管管壁材料的弹性模量,Eg=
2.1×106kg·f/cm2;
μ——钢管管壁的泊桑比,μ=0.3;
g——重力加速度,g=9.81m/s2;
n——钢管的振动模数,取n=2,3,4;
l——钢管的跨距,l=800cm;
q——计算部位的平均静压力(kg·f/cm2);
rg——管壁材料的比重,rg=7.85t/m3=7.85×10-3kg/cm3;
α——数值系数,最小取α≤1/n。
公式(1)中各项数值的计算:

公式 中其余计算过程及成果见表 表
7。
表1 计算结果

表1 计算结果
?

表2 计算结果

表2 计算结果
?

表3 η/(1-μ2)计算结果
表4 计算结果

表4 计算结果
?
表5 计算结果
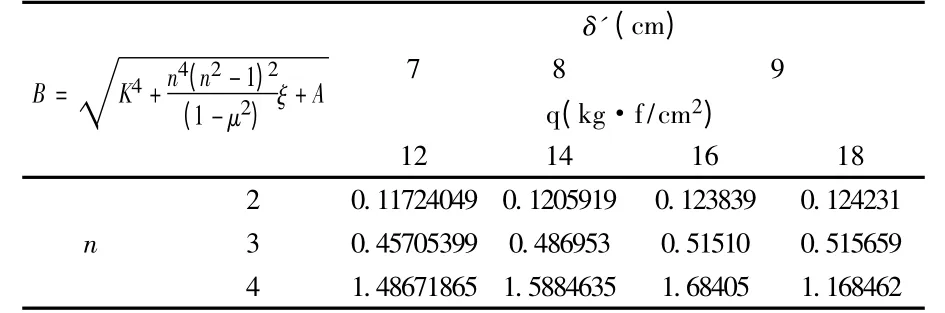
表5 计算结果
?
表6 计算结果

表6 计算结果
?

表7 fμ值计算成果
4 压力波及旋转涡流引起的振动频率计算
高压水流冲击叶片形成的压力波及尾水管内旋转涡流引起的振动频率计算如下:
高压水流冲击叶片形成的压力波引起的振动频率f2为:
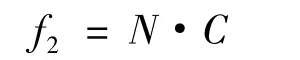
式中:C——为转轮叶片个数,C=17;
N——水轮机转速,N=7.142833转/s;
f2=7.142833×17=121.428161(次/s)。
尾水管内旋转涡流引起的振动频率f1为:
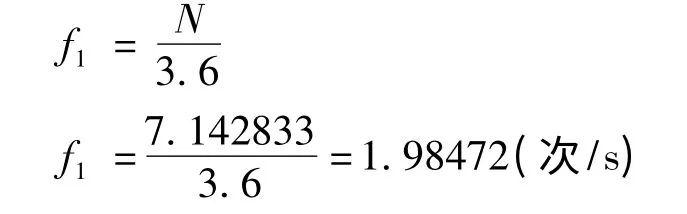
5 结论
经过计算,可知各段压力钢管的固有频率与外界引起的振动频率不发生耦合。

