基于Matlab 的七参数空间坐标转换研究与实现

刘 平，段志强，谢 超

（1.湖北省测绘成果档案馆，湖北 武汉 430074）

基于Matlab 的七参数空间坐标转换研究与实现

刘 平1，段志强1，谢 超1

（1.湖北省测绘成果档案馆，湖北 武汉 430074）

分析了七参数空间坐标转换模型和Matlab语言在矩阵运算方面的优势。在此基础上开发实现了七参数空间坐标转换程序。简要介绍了利用Matlab语言开发此程序的一点体会。

Matlab；七参数；空间坐标转换

1 七参数空间坐标转换基本原理

坐标系统间的差异主要来自于坐标系统的定义差，即原点位置、坐标轴向的定向和尺度的定义差。坐标转换时应优先考虑坐标系统定义差异的转换，即首先应完成相似变换。在相似变换的基础上，再考虑对剩余误差进行拟合，使精度较低的坐标框架点附合到精度较高的坐标系统的框架点坐标，使统一后的坐标系框架点坐标具有较好的一致性。

七参数空间坐标转换，实际上是2个不同基准面之间的空间直角坐标的相似变换。其基本原理是：假设2个坐标基准都满足“刚体”（基准无变形）条件，则2个不同基准间存在3个平移量和3个旋转量及1个尺度变换量的差别。

对于既有旋转、缩放又有平移的2个空间直角坐标系的坐标换算，存在3个平移参数和3个旋转参数以及1个尺度变化参数，共7个参数。其坐标转换数学模型为：

一般εX、εY、εZ为微小转角，可取：

cosεX=cosεY=cosεZ=1

sinεX= εX，sinεY= εY，sinεZ= εZsinεXsinεY=sinεXsinεZ=sinεYsinεZ=0于是有：

式（1）即为布尔沙-沃尔夫七参数空间坐标转换模型。此模型的转换步骤是首先作三轴旋转，再统一尺度，最后再平移。如果能求解出这7个参数值，则所有待转换点的坐标转换也就可以求得了。公式中含有7个转换参数，为了求得7个转换参数，至少需要3个公共点（也称为重合点），当多于3个公共点时，可按最小二乘法求得7个参数的最或是值。

则可写出如下形式的误差方程：改写成矩阵形式为：

式中，δX =（∆X0，∆Y0，∆Z0，a1，a2，a3，a4）T，为待求点转换参数向量；V =（VX2i，VY2i，VZ2i）T为改正数向量；L=（X2i，Y2i，Z2i）T已知值；B为系数矩阵。

根据最小二乘法原理，可列出法方程为：

其解为：

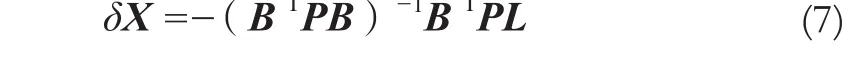
当已知公共点为等精度时，上述权矩阵为单位权矩阵，于是有：

单位权方差：

式中，n为参与求解转换参数的点数。

2 七参数空间坐标转换技术流程

1）收集整理（或施测）坐标转换区域范围的已知公共点空间坐标成果；

2）分析选取用于计算坐标转换参数的公共点，原则是选取能覆盖转换区域且精度较高、分布均匀的已知公共点成果；

3）根据上述七参数模型计算坐标转换参数；

4）分析用于计算坐标转换参数的公共点的坐标转换残差和残差中误差，以及未参与求解参数的公共检查点坐标转换残差和残差中误差，查找并剔除用于计算坐标转换参数的粗差公共点；

5）用可靠公共点重新计算坐标转换参数，直到精度满足规定限差为止。

6）根据最终合格的转换参数，代入式（2），求解出所有待转换点的转换坐标。

如果已知公共点是高斯平面坐标，则在作七参数坐标转换前需要将其经高斯投影反算得到大地经纬度B、L，而大地高H=正常高+高程异常。然后再根据同基准下的大地坐标与空间坐标转换关系，将大地坐标转换成空间坐标。

3 七参数空间坐标转换研究与实现

3.1 问题的分析处理

根据矩阵理论知，方程个数大于未知量个数的方程组称为“超定方程组”。求解坐标系转换参数的计算中，一般都要求有多余的公共点参与，即在解求7个转换参数（7个未知数）时，方程个数往往远大于7，显然坐标转换计算过程所涉及的都是“超定方程组”。求解“超定方程组”比较常用的方法是最小二乘法。形象地说，就是在无法完全满足所给定条件的情况下，求解“超定方程组”的一个最或是解。

从上述坐标转换数学模型可知，在合理选择了参与求解转换参数的公共点和外部检查点后，坐标转换过程其实质是根据参与求解转换参数的公共点数量，动态组成B矩阵和L矩阵（随着参与求解坐标转换参数的公共点增加，B矩阵和L矩阵也不断增大）。然后对数值矩阵进行一系列的运算，而其中关键运算是矩阵求逆。在Matlab中，对形如Ax=b的矩阵方程作求逆运算，一般可用“左除”、内部数值求逆函数求逆及符号运算求逆函数求逆等。

上述式（7）或式（8）中矩阵B为3n×7阶的矩阵（n为参与求解参数的公共点数），当参与求解参数的公共点为5个时，其B矩阵是一个15×7阶的矩阵。显然，对B矩阵求逆运算将是很复杂且运算量很大的工作。在矩阵求逆过程中，如果矩阵接近奇异，Matlab将给出警告信息。

由于参与求解坐标转换参数点的坐标值X1i、Y1i、Z1i都很大（一般都有十进制的7位整数），而系数矩阵B中其他元素仅为1或0，即系数矩阵B的向量之间长度过于悬殊，致使矩阵B的条件数过大，且BTB的条件数更大，即此时矩阵呈病态趋势（或称矩阵接近奇异），求逆时容易产生扰动，造成求解的转换参数可能不正确。

对上述警告性提示，笔者采用了2种方法处理。一是首先对坐标进行重心化处理，将所有点的坐标平移到重心化坐标系中，减小坐标的绝对值。求逆完成后，在适当处再反算还原到原坐标系中。经过这样处理后，警告提示就再没有出现了。另一种方法是采用Matlab中符号矩阵求逆运算，因矩阵中变量元素是符号变量，即变量没有赋值，避开了数值矩阵求逆而进行符号矩阵求逆，从而避免因数值计算误差导致的矩阵接近奇异的情况发生，完成求逆运算后再用相关函数将符号矩阵转换成数值矩阵，也可避免出现“矩阵接近奇异…”的警告提示。

3.2 七参数空间坐标转换的实现

先用自编程序将区域散点展绘到图上，根据图上点的分布，均匀选择参与求解转换参数的重合点，再将待转换坐标系下所有点的空间坐标和目标坐标系下的重合点空间坐标建立一个文本文件保存，然后启动程序。程序设计上首先通过界面提示输入参与求解转换参数的重合点个数，并默认重合定向点（即参与求解参数的重合点）为5，且最少要大于或等于3个，如输入重合点数小于3，程序会提示输入错误。再通过界面分别选择待转换坐标系所有点坐标文件和目标坐标系公共点坐标文件，程序将2个文件中的空间坐标数据分别保存到2个矩阵变量中。通过对坐标系重心化处理及一系列运算，计算出转换坐标、各点残差及残差中误差以及单位权中误差和7个转换参数等，并将所有结果保存到Excel表格中。

3.3 程序正确性验证

1）经多个区域实例数据计算（网上很多实例数据及结果）对比，程序计算结果完全正确。

2）将七参数空间坐标转换出的结果再转换到大地坐标，然后继续经投影正算到高斯坐标，对比其原始高斯坐标成果，结果所有同名点差值也都小于1 mm。

3）还开发了一个平面四参数坐标转换程序，对同一区域作平面四参数坐标转换，并与七参数坐标转换程序结果对比，转换计算出的坐标值几乎完全一致，证明了2个独立开发的坐标转换程序完全正确。

[1] 孔祥元．大地测量学基础[M]．武汉:武汉大学出版社,2006

[2] 张志涌．精通Matlab[M]．北京:北京航空航天大学出版社,2003

[3] Moler C．Matlab 数值计算[M]．北京:机械工业出版社,2006

[4] 肖筱南．现代数值计算方法[M]．北京:北京大学出版社,2003

[5] 同济大学数学教研室．工程数学线性代数[M]．北京:高等教育出版社,1982

[6] 成英燕,李夕银．适用于不同椭球的高斯平面坐标正反算的实用算法[J]．测绘科学,2004,29(4):26-27

[7] 刘陶胜,黄声享,罗力,等．基于重心基准的平面坐标转换研究[J]．大地测量与地球动力学,2011,31(2):102-106

[8] 陈宇,白征东,罗腾,等．基于改进的布尔沙模型的坐标转换方法[J]．大地测量与地球动力学,2010,30(3):71-75

[9] 李潇,尹晖．基于最小二乘配置的三维空间坐标转换[J]．测绘工程,2008,17(2):16-18,29

[10] 刘平,吕海兵,张峰,等．数值计算误差初步理解及简单分析[J]．地理空间信息,2011,9(3): 156-158

P226

B

1672-4623（2014）06-0062-03

10.3969/j.issn.1672-4623.2014.06.022

刘平，正高职高级工程师，主要从事测绘地理信息内业技术和质量管理工作。

2014-01-26。