Particle-Based Moving Interface Method for The Study of the Interaction Between Soft Colloid Particles and Immersed Fibrous Network
Louis C.Foucard,John Pellegrinoand Franck J.Vernerey,2
1 Introduction
Filtration membranes are ubiquitous to most biological systems and are at the heart of important applications in bio-medical engineering[Baker(2004);Desai,Hansford,Nashat,Rasi,Tu,Wang,Zhang,and Ferrari(2000)],food industry and both fossil and renewable fuels processes[Cheryan(2005)].In the majority of these applications,membranes are used to either(a)separate undesired particles from a solution or(b)produce(and fractionate)stable emulsions with specific size controls(such as liposomes)used in medical diagnosis and therapy[Cevc(2004)].In addition,a novel area of biological medicine is drug delivery using liposomes[Gregoriadis and Florence(1993);Allen and Cullis(2013)].A liposome is a micronsized vesicle(bubble)whose interfacial surface is stabilized by lipids.The interior of the liposome can be filled with drugs to be delivered for treatment of various diseases.Filtration of fluids containing liposomes are required at various steps within their manufacture and delivery to patients,in order to provide sterility.These filtration steps can require both allowing liposomes to freely pass through the porous filter,while retaining possible biological contaminants,as well as,retaining and concentrating the liposomes.Despite the very soft nature of these colloidal particles,current membrane designs have consistently relied on the assumptions that they are rigid particles[Faibish,Elimelech,and Cohen(1998);Song(1998);Hoek,Kim,and Elimelech(2002)].In fact,it has only been in recent years that hindrance factors for transport of non-spheroidal(rod)shaped rigid particles in ideal pores has been theoretically addressed[Baltus,Badireddy,Xu,and Chellam(2009);Dechadilok and Deen(2006)].This has strongly hindered the performance of current membrane systems.The incorporation of deformation is,however,expected to critically affect the above mechanisms since particles can easily change their shape to accommodate a variety of pore shapes and sizes(Fig.1).It can also increase the adhesion between a particle and a surface(by effectively increasing the contact surface area)and thus hinder particle entry and permeation.
From a computational modeling viewpoint,studies of the mechanics of soft vesicles and their interactions with an immersed porous network has been hindered by a number of theoretical challenges,which include the coupled fluid-structure interactions,intense particle deformations and perhaps separation,as well as the effect of surface forces that are very significant at micron(and lower)length scales.Furthermore,when fibers are present,the geometry of sharp tips create singular flow fields which have been resolved through the use of refinement methods[Alleborn,Nandakumar,Raszillier,and Durst(1997);Mullin,Seddon,Mantle,and Sederman(2009)].Such approaches are not only costly but can never truly resolve the steep gradient and hyperbolic pressure field that appears at the fiber tips[Moffatt(1963)].Regarding modeling immersed vesicles,one of the most acknowledged methods is the Immersed Boundary Method[Peskin(1972)],which basically relies on three features.First,the fluid flow equations are handled with an classical Eulerian approach.Second,the deformation of the vesicle’s boundary(which can be described as a shell,membrane or bi- fluid interface)is done within a Lagrangian frame and third,the fluid-structure interactions are handled via a forcing term that is localized on the membrane domain.Numerous biological problems were approached in this manner,such as red blood cell motion[Eggleton and Popel(1998)],or cell growth and division[Li,Yun,and Kim(2011);Dillon,Owen,and Painter(2008)].Later improvement of the method includes the Immersed Finite Element Method[Zhang,Gerstenberger,and Wang(2002)],where the Lagrangian solid mesh evolves on top of a background Eulerian mesh that covers the entire computational domain.This simplifies greatly the mesh generation. Another computational method for the treatment of fluid-solid interactions is the Immersed Particle Method,where both the fluid and the structure are described using Lagrangian mesh free particles[Rabczuk,Gracie,Hsong,and Belytschko(2000)].However,due to the lagrangian treatment of interfaces,these methods becomes cumbersome when extreme deformations and subsequently severe distortions of the finite element mesh or the particle distribution are observed.The use of mesh regularization techniques[Ma and Klug(2008)]may provide a solution but they remain computationally expensive.When studying vesicle permeation through porous media,a second challenge is to link macroscopic models,traditionally casted in terms of Darcy’s law Chen,Huan,and Ma(2006)to the micromechanics of vesicle transport through a network.Linking two very disparate length-scales is a long standing issue in computational methods as they typically lead to simulation sizes that are too large to be computationally efficient,if feasible.
To address these issues,the objectives of the work are two-folds.First,we integrate a recently developed Particle-based Moving Interface Method(PMIM)[Foucard and Vernerey(2014b)]to describe the mechanics of immersed and porous interfaces[Vernerey(2011,2012)]with a numerical technique to describe creeping flow through a fibrous network[Foucard and Vernerey(2014a)].In this framework,the motion of an immersed soft vesicle is coupled with an Eulerian fluid description via a particle-enriched interface that can evolve as dictated by mechanical force equilibrium.Using an updated Lagrangian description of the vesicle,the motion of the deformable vesicle is completely independent from the spatial numerical discretization and it enables a very precise description of the curvature and motion of the vesicle over time.The method also use a enriched finite element approach to match the analytical asymptotic fields near the tip of fibers to smoothen far- field velocity and pressure fields.This ensures that a high fidelity solution is obtained without using refinement techniques.Note that the model is p-resented in two dimensions and fibers can actually be better described as plates that extend to in finity in the third dimension.The second contribution of the paper is the introduction of a homogenization approach,inspired by research efforts in solid mechanics[Vernerey,Liu,and Moran(2007)],to bridge the microscale mechanics of flow and vesicle transport to the estimation of the macroscale permeability of the network.For this,we introduce a so-called elementary volume element in which one can computationally average the flux of fluid/vesicles subjected to macroscopic pressure gradients.This operation eventually permits the determination of macroscopic network permeabilities as illustrated in subsequent examples.To showcase the potential of the method,we then predict the role of a microscopic parameter,the surface tension at the vesicle-solvent interface,on the overall permeation of particles through the network.This study highlights the role of surface tension,pressure differential and porosity configuration on the entry and perhaps immobilization of the vesicle within a porous media.It should be noted that in our current model,the colloidal vesicle is actually a deformable fluid"cylinder"that extent in the third dimension.The closest physical embodiment of this type of vesicles might be coalescing media for oil in water separations.
The paper is organized as follows.In the next section,we provide a mathematical description to describe the deformation of a soft fluid-like colloid interacting with an immersed fibrous network.In section 3,we then discuss the numerical formulation based on a mixed- finite element and particle method.Section 4 then concentrates on the derivation of a homogenization technique that bridges the micro-mechanisms of vesicle permeation to macroscopic permeabilities.We finally conclude the paper with a discussion of the method,results and potential for improvement.
2 Multiscale mathematical formulation for a soft droplet in an immersed fibrous network
2.1 Basic governing equations
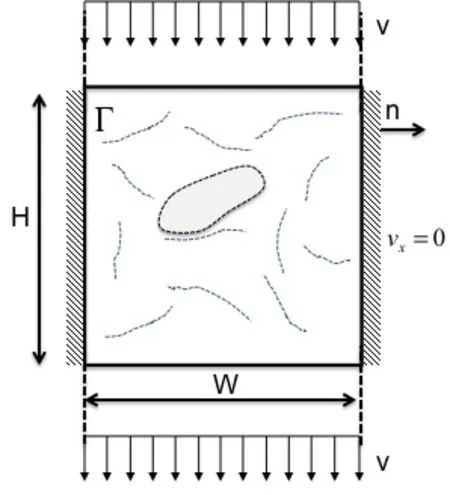
Consider a two-dimensional incompressible viscous flow in a domain Ω delimited by a boundary ∂Ω in which exists one or multiple no-slip rigid boundaries ΓFtaking the shape of thin fibers(or plates)(Fig.1).We also consider a number of closed vesicles,with boundaries ΓIand that are able to move with the surrounding fluid.The problem is characterized by the Reynolds number Re=HVρ/µ whereHis the characteristic length scale,Vthe characteristic fluid velocity,µ the kinematic viscosity and ρ the fluid densities in and out of the vesicles.We choose here to remain in the Stokes flow assumption with Re?1,where inertial effect may be neglected.The velocity of a fluid particle is given in terms of its material time derivative v(x,t)=Dx/Dt,where x={x y}is the current position of the fluid particle at timet.Under these conditions,the governing equations and boundary conditions for the Stokes flow are written:
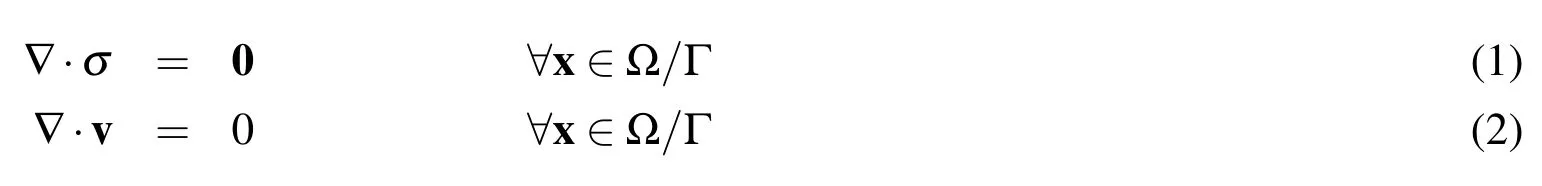
where σ is the Cauchy stress tensor in the fluid and the second equation imposes the condition of incompressibility.These equations are combined with the moving interface problem:
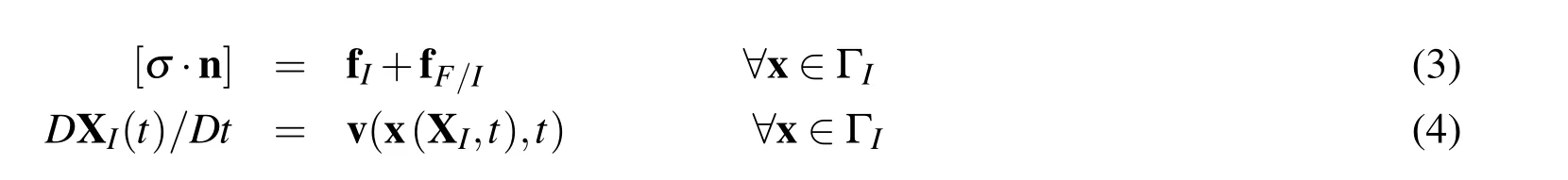
Here XIdenotes a point on the vesicle boundary,the vector n represent the normal direction to the moving interface,the force fIis the unbalanced interface force due to its deformation and fF/Iis the interaction force between fibers and the moving interface.Finally,the boundary conditions for fluid motion on the external boundary and on fibers read:

wherep0is an external pressure surrounding the domain Ω,and a zero-velocity condition is applied on the fiber domain.The latter assumption arises from the model that(a)the fiber are rigid and(b)a no-slip condition is assumed between the fluid and the fibers.
2.2 Constitutive equations
To complement the above system of equation,a number of constitutive relation must be introduced.They can be broken down into three components that describe in turns:(a)the behavior of the fluid,(b)the mechanical behavior of the interface and(c)the interactions forces between interface and fibers.In this work,we consider a simple incompressible Newtownian fluid with viscosity µ that can be different within the colloids and the external fluid.

where D is the rate of deformation andpis the hydrostatic pressure enforcing the incompressibility condition.For the sake of simplicity,we consider here a bi- fluid interface without elastic stiffness and characterized by the liquid-liquid surface tension γ between the vesicle and the continuum fluid.More complex cases can later be considered as discussed in[Foucard and Vernerey(2014b)].In these conditions,the force fIof the interface can be written:

with H the mean curvature of the surface,computed in section 3.3.Finally,the fiber-interface interaction forces is considered to be of repulsive nature at short distance.For this initial modeling effort,we have used an interaction energy function of the same form as the electrostatic potential function.That is,the force is inversely proportional to the distance between hypothetical point charges on the surface of the flake( fiber):

where φFis the distance function with respect to the fiber.Future work can incorporate more complex formulations including van derWaals interactions.
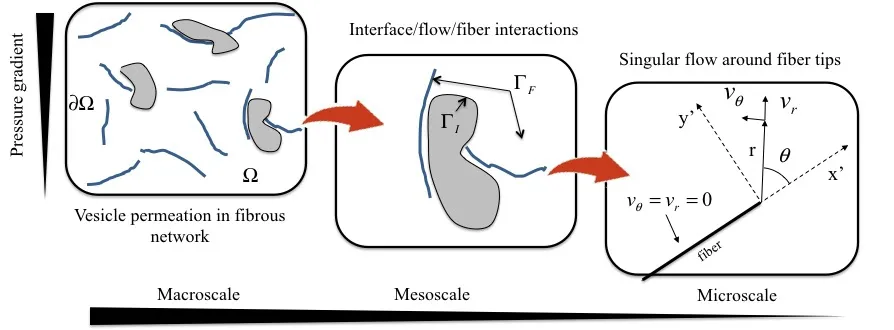
Figure 1: fluid domain Ω,interface ΓIand fixed structure ΓFwith no-slip/nopenetration boundary condition.The local polar coordinate system is centred at the fiber tip and oriented in the direction of the fiber.
2.3 A two-scale asymptotic solution to describe the fluid flow around thin fibers
When the diameter of fibers constituting the network is very small compared to characteristic size of a particle,the above mathematical problem admits a solution that displays variation across three disparate length-scales(Fig.1):macroscopic fields variations are on the order of the domain size,mesoscopic variations are on the order of the particle size and finally,microscopic fields vary on the order of the fiber diameter size.This creates a significant issue to later derive an accurate numerical solution at a reasonable computational cost.Inspired by asymptotic methods[Hawa and Rusak(2002);Moës,Dolbow,and Belytschko(1999)],we here propose to address the problem as follows;First,we derive a solution for the fluid flow around the tip of a fiber and subjected to the far- fields boundary conditions.Then,we enrich our macroscopic solution with this solution in the regions of interests,which result in introducing a limited number of"microscopic"degrees of freedom.Finally,we compute a solution that ensures that both microscopic and mesoscopic are consistent within the entire computational domain.

where α is an unknown complex exponent that determines the structure of the flow,and is to be found as part of the solution.Following[Moffatt(1963)],the functionfα(θ)is written:
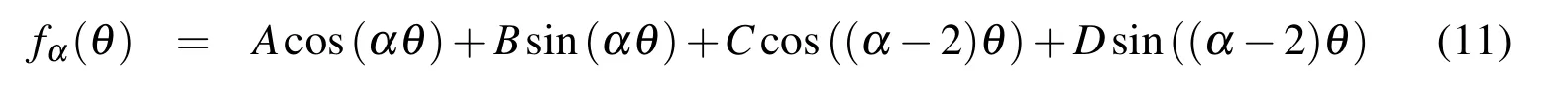
whereA,B,CandDare arbitrary complex constants.In the cases where α=0,1 or 2,the above equation degenerates into other forms that are not relevant to the problem studied here,and we will henceforth only consider values of α such that α 6=0,1,2.The axial and radial velocities of the flow are deduced from the stream function ψ(r,θ)as follows:

and are subjected to the following no-slip/no-penetration boundary conditions at the wall:

Enforcing these boundary conditions on(12)and(11)yields the constantA,B,CandD[Moffatt(1963)]:
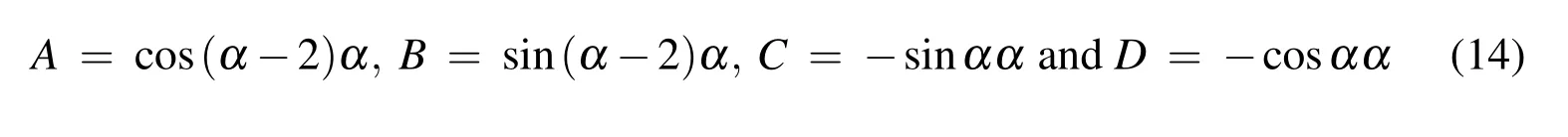
as well as the exponent α ,found to be α =3/2 in the particular case of in finitesimally thin fibers[Moffatt(1963)].The pressure can then be calculated by solving the momentum equation

where v=vrer+vθeθis computed using equations(10)and(12).
3 Numerical approach:the Particle Enriched Moving Interface Method
The idea of the Extended Finite Element Method is to enrich a finite element space with additional functions.Our numerical technique takes the same approach:the Stokes flow is solved using the traditional C0conforming finite elements(in our cases 4 node bilinear elements for the pressure and 9 node quadratic elements for the velocity)space,and we enrich this space with additional degrees of freedom that allow the pressure jump across the interface(the velocity stays continuous)and singular pressure and velocity fields around the corner tip.To enrich the standard finite element space,we make use of the linearity of the Stokes flow and simply sum the enrichments for the pressure jump and the asymptotic solution around the corner tip.The velocity and pressure fields in this enriched space are therefore interpolated as follows:
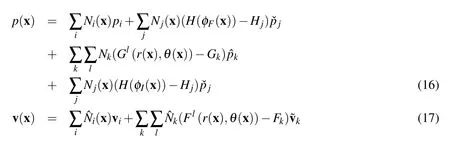
whereNandˆNare the regular 4 nodes and 9 nodes shape functions,His the Heaviside function that provides the needed discontinuity,and F and G are the special asymptotic corner tip functions.The terms φIand φFdenote level-set functions,i.e.the signed distance functions with respect to the interface and the fibers.Table 1 shows a summary of asymptotic functions used as enrichment for both pressure and velocity fields[Foucard and Vernerey(2014a)]:The termsˇpjandˆpjcorrespond to the enriched degrees of freedom associated with the jump in pressure across the fibers and the droplet interface respectively,while the terms˜pkand˜vkare the enrichment degrees of freedom associated with the near corner tip pressure and velocity fields.In addition to the velocity and pressure degrees of freedom and their

Table 1:Corner tip asymptotic functions
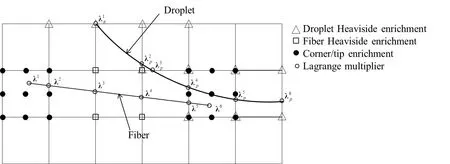
Figure 2:Black dots denote tip enrichment for the velocity and pressure(only the four corner nodes in the case of the pressure)while squares and triangles indicate split enrichment for the pressure for the fibers and the interface respectively.

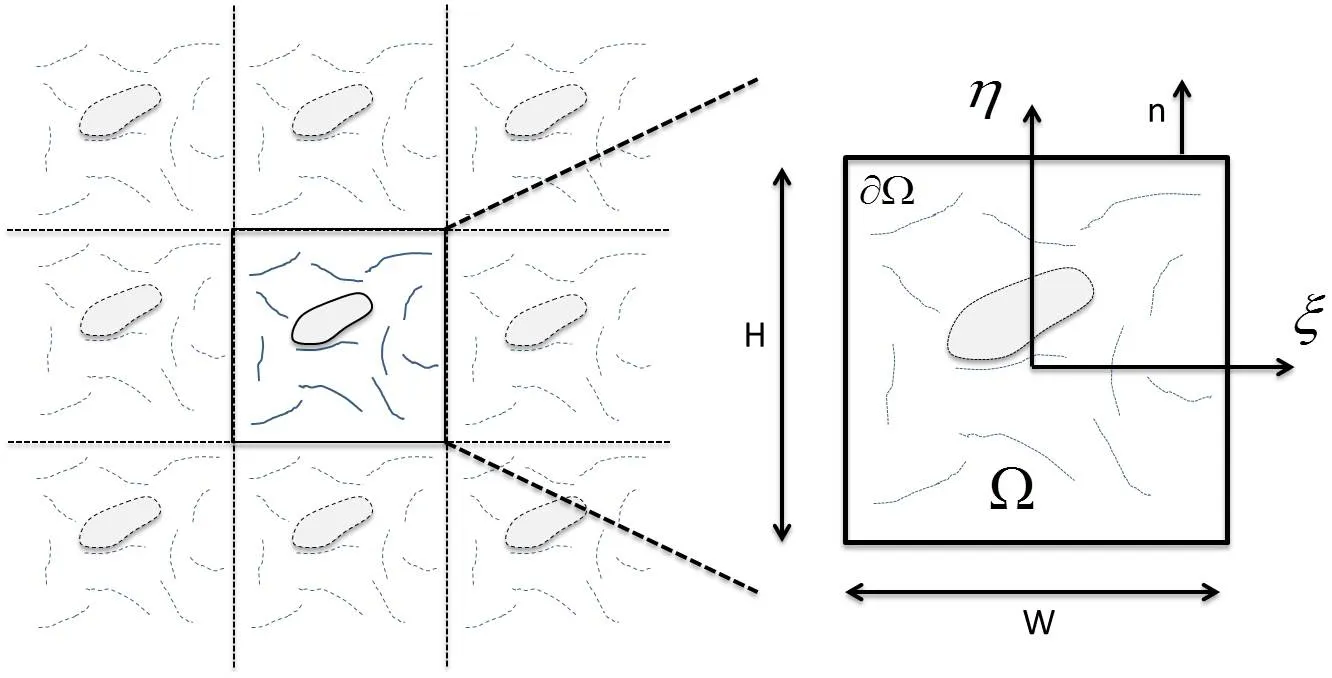
3.1 Weak formulation
Introducing the test functions wv,wp,wλandwλp,integrating by parts and using the divergence theorem,the weak form of the governing equations(1)-(5)in the f l uid domain can be written as:given the position XIat timet, find v∈V,p∈P,
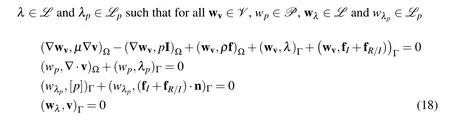
where the notation(·,·)Ωindicates theL2inner product with respect to the domain Ω.The Lagrange multipliers λ and λpenforce the no-slip/no-penetration boundary conditions(6)and the pressure jump conditions on the implicitly defined corner walls.The test functions wλandwλpare associated with the Lagrange multipliers and V,P,L and Lpare admissible spaces for the velocity, pressure and Lagrange multipliers.
3.2 Discretized form
The weak form(18)is then discretized in space by using the XFEM approximation,and after simplifications yields the following linear system:

where Ktis the consistent tangent matrix,dt={vpλpλ}the global vector of unknowns and ftthe global force vector at timet.The element contribution to Ktand ftare as follows:
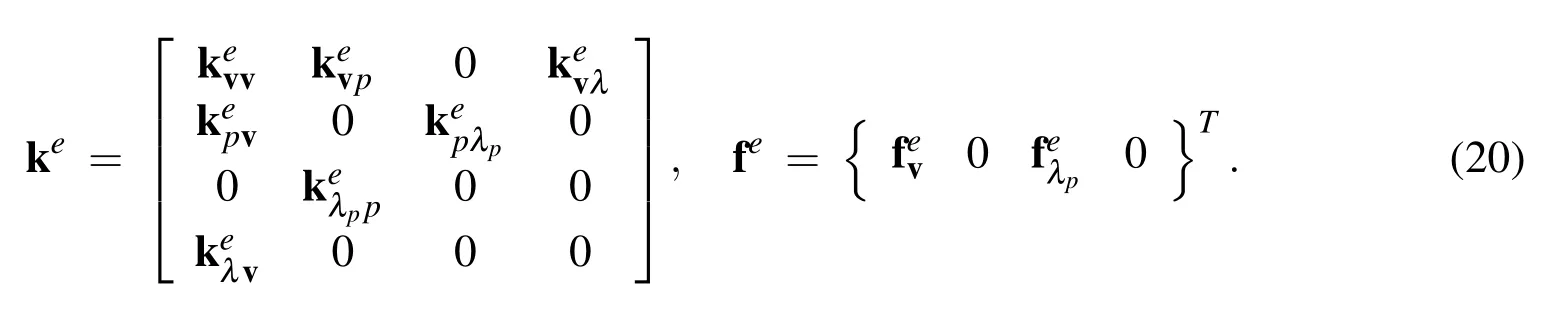
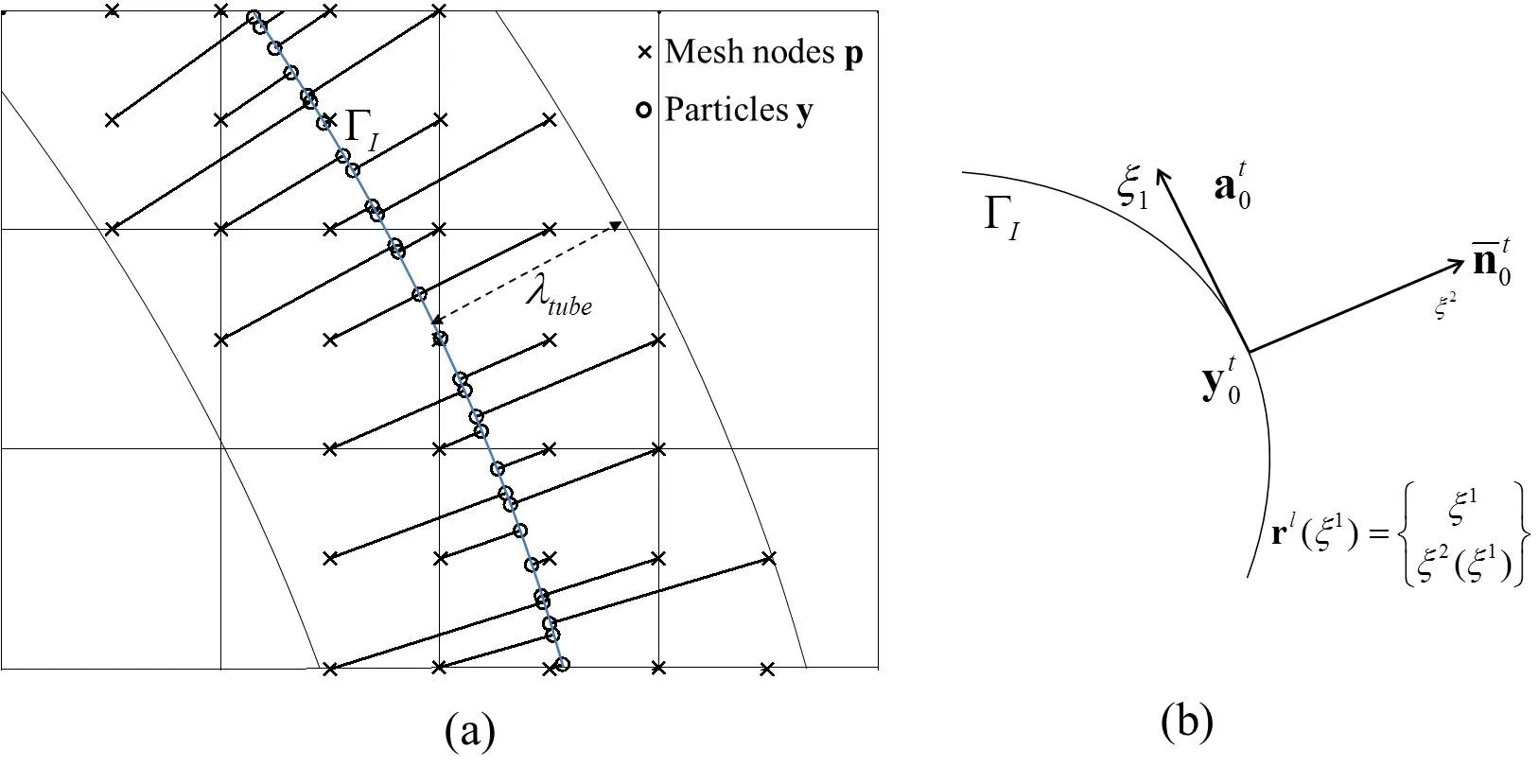
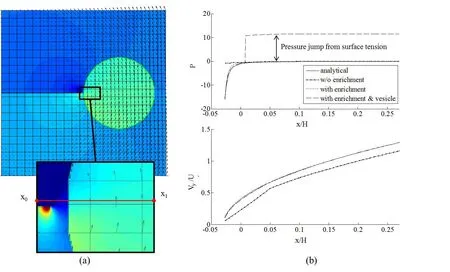
The form of the components in the kematrix and and the feare given in appendix A.The finite element equation(19)can be solved with a linear solver to yield an expression for the fluid(and interface)velocity v at time t.Given the interface velocity v,the position XIof the vesicle interface ΓIis then updated to compute Kt+dtand ft+dtfor the next time step,withdtthe time step increment.Once the vesicle has left the computational domain,or once||dt+dt−dt|| To track the deformation of the interface ΓI,we choose here to use a grid-based particle method similar to what was introduced in[Leung,Lowengrub,and Zhao(2011)].This method indeed possesses the double advantage of tracking the interface explicitly with particles while using the underlying fixed finite element mesh to ensure a fairly uniform repartition of the particles on the interface.Here we summarize the grid based particle method and discuss the update of the interface position and deformations measures.The particles,whose position vector is denoted by y,are chosen as the normal projection of the underlying mesh nodes,with position vector p,on Γ(Fig.3a.).Initially,the interface is described implicitly as the zero level-set of a signed distance function φI(p,t=0).The initial coordinates of particles y can then found as follows: To limit the number of particles,we define a so-called computational tube such that only nodes p whose distance to ΓIis smaller than a cut-off value λtubeare accounted for.It is important to note here that there is a one to one correspondence between each particle y and node p.This ensure a quasi-uniform repartition of particles along the interface throughout its evolution.Between two subsequent time steps,the particles are moved according to the normal component of the interface velocity v⊥(ξ,t)as follows: where Ω is the matricial form of the angular velocity of the interface normal[Jason and Kumar(2012)]: with εijkthe permutation tensor and ξ1the local coordinate running along the interface(Fig.3b.).After the motion of the interface,the particles y may not be the closest point on ΓIto their associated nodes p.Moreover,the motion of the particles may cause their distribution on ΓIto become uneven,which can affect the geometrical resolution of the interface.To overcome this issue,the interface is ressampled after motion by recomputing the particles as the closest points on ΓIto the nodes p inside the updated computational tube(which has moved with the interface)(Fig.3a.).This is done by first approximating the interface with polynomials locally around each particle.The procedure,explained here in the two dimensional Figure 3:(a)particles and associated nodes in the computational tube.(b)Local polynomial approximation of the surface(and of any Lagrangian field).The polynomial ξ 3(ξ 1,ξ 2)that approximates the interface is constructed via least square fitting using neighbouring particles in the local referential{a0,}centered on particle y0. The relationship between the local parameterization rl(ξ1)and the global parameterization XI(ξ1)defined in section 2.1 is then found via rotation and translation operations in the form: Here we investigate the accuracy of the numerical technique by comparing it with the analytical solution developed by Moffat[Moffatt(1963)]for the velocity and the pressure field around the fiber tip,with and without a circular droplet in the vicinity.The velocity given by the analytical solution is imposed at the boundary of the computational domain.The Reynolds number is given by: with µ the kinematic viscosity andVthe fluid velocity away from the corner.The parametersVand µ are chosen such that Re?1 everywhere in the computational domain.The error made in computing the velocity of the flow near a corner is calculated as follows: Figure 4:Error Evmade in computing the flow velocity around the corner tip in mode I and II,for different corner angle α.The error can be lessened by more then a factor of 10 using corner tip enrichment. where vnumdenotes the velocity calculated using the numerical method,vasympthe asymptotic solution and x0,x1two points in the vicinity of the fiber tip(Fig.4a.). Table 2:Error made in computing the pressure and velocity fields Epand Ev,without enrichment,with enrichment and with a vesicle in the vicinity of the fiber tip. The circular vesicle in the neighbourhood of the fiber tip is shown in Fig.4a.,as well as a close up of the singular pressure field around the fiber tip and the pressure jump across the vesicle interface.Fig.4b.shows the velocity and the pressure field in the neighbourhood of the fiber tip,along the line from point x0to x1.We observe in table 2 that without enrichment,the errorsEvandEpare fairly high,at 18.2%and 22.1%respectively.However,the incorporation of the tip enrichment developed above reduces the errors down to 0.7%and 3.1%respectively.The presence of a circular vesicle in the vicinity of the fiber tip does not significantly affect the accuracy of the scheme,and we can note the appearance of a pressure jump across the vesicle interface from its surface tension,as expected.The source of the remaining error stems from the weak enforcement of the no-slip/no-penetration condition on the corner wall.Future studies will investigate reducing the error by using quadratic instead of linear shape function for the interpolation of Lagrange multipliers.Overall,the numerical technique presented here is shown to significantly increase the accuracy of the simulation of a flow near a sharp corner using the extended finite element method,at a much lesser computational cost than classical methods since no mesh refinement is needed. In this section,we present a generalized homogenization scheme to determine how different phases of a fluid(such as solvent or various vesicles present in the solvent)can permeate through a fibrous filtration membrane.For this,we first present a general homogenization scheme based on the Hill-Mendel conditions that then served as a basis to express macroscopic permeabilities in terms of flux and pressure on the boundary of a volume element.We then apply these concepts to the specific problem of soft vesicles travelling through a small fibrous network and pay particular attention to the role of surface tension at the vesicle-solvent interface. From a macroscopic viewpoint, the phenomenon of fluid flow through porous media has traditionally been described by Darcy’s law relating volumic flux to pressure gradient throughout a porous network.The relationship between the fluxof fluid α and the macroscopic pressure gradientis established via the definition of so-called macroscopic permeability tensor καin the form where µαis the fluid viscosity.We note that for isotropic porous network such as those studied in this paper,the permeability can be expressed in terms of a single scalar quantity καsuch that κα= καI with I representing the second order identity tensor. Figure 5:Periodic assumption of a fibrous network with a population of permeating particles.A unit periodic cell is identified and analysized to extract the macroscopic properties of the network. It is clear here that the quantity καrepresents the ease by which a fluid permeated through the network.Theoretically,it may therefore be determined through a thorough study of the micromechanisms of vesicle flow and deformation and a consistent averaging operation to bridge micro to macroscale.We propose here to use classical homogenization theory where we assume that at the mesoscale,a membrane is made of a periodic array of unit cells comprised of a pseudo-random fiber distribution.For the sake of simplicity,we also assume that a number of vesicles can be found within each of these cells and that they all have the same position relative the their corresponding unit cells(Fig.5).For each elementary volume(of dimension,W×H),it is possible to introduce a local coordinate system(ξ,η)whose origin is at the center of the volume.With this,it is possible to express the microscopic pressure fieldpin such a domain as a first order expansion as follows: with n the unit vector normal to the boundary Γ andV0the volume of the domain.Note that we used the divergence theorem to obtain the last equality.The above relation is particularly useful as it enables to characterise the macroscopic pressure gradient in terms of the microscopic pressure field on the boundary of the unit cell.We also obtain that In other words,the macroscopic average of the microscopic fluctuation fields identically vanish.To further establish a relationship between fluxes and pressure gradients,we invoke the Hill-Mendel condition on energy dissipation.More precisely,we postulate that the macroscopic energy dissipation per unit volume and time is equal to the average of the microscopic dissipation over the elementary volume and during a characteristic time period∆t.Note that this elementary time increment is related to the time needed for a vesicle α to go through the elementary volume.We write: On the left hand side, we expressed the energy dissipation of a Darcy-type flow over a volumeV0=W×H×1 and a period∆t.On the right hand side,we expressed this same energy in terms of the product of surface forcespn wherepis the pressure and n the normal to the boundary,and the velocity v of fluid particle moving across the boundary.Substituting the expression(35)forpinto(38)and identifying the terms,one can show that: This establishes a relation between the macroscopic volumic fluxand the microscopic flux qαacross the boundary of the elementary volume.The macroscopic permeability can then be numerically determined by relating the macroscopic flux(39)to pressure gradient(43)via equation(34). Figure 6:Schematic of the geometry,dimensions and boundary conditions for assessing the permeation of a soft colloid particle through a fibrous network. Let us now apply the above findings to the computation of a network permeability to two fluids:(a)the solvent and(b)the immersed vesicles.To simplify the analysis,we consider a two-dimensional vertical porous flow(Fig.6)for which boundary conditions are given in terms of the macroscopic solvent flowqs=Vand a no- flux boundary condition on the left and right boundaries of the domain.The relevant quantities to compute are therefore(a)the overall vertical solvent flux,(b)the overall vertical vesicle fluxand the vertical macroscopic pressure gradientFor each simulation,the elementary time∆tis computed as the time required for a vesicle to travel the entire(vertical)length of the domain. Flux.For this particular problem,the homogenization relation(39)becomes,for the solvent: where the final equality was obtained by realizing that the volumic flux of the fluid across the boundary is constant in time.The volumic flux of vesicle can similary be computed by: where we used the fact that for incompressible fluids,the cumulative volumic flux entering the domain during a time interval∆tis equal to the volume Ωvin the vesicle.In other words,we have: This relation,together with the expression of the volume fraction of a vesiclefv=Ωv/(WH)yields the second equality in(41).This result indicates that the volumic flux of vesicles is proportional to their volume fraction and inversely proportional to the time∆tneeded to travel a vertical distanceHin the network. Pressure gradient.As mentioned above,we are here interested in computing the vertical macroscopic velocity gradientUsing(43)for the geometry shown in Fig.6,it is straightforward to show that: Numerically,the above spatial integrals over the top and bottom boundaries of the domain can be evaluated using a surface gausian quadrature rule while the time integral can be evaluated using the trapezoidal rule. Macroscopic permeabilitiesWith the knowledge of(40),(41)and(43),it is now possible to compute the macroscopic permeabilities of the network.Indeed,writing(34)in the vertical direction,it is straightforward to show that: In summary,our numerical approach can be divided into four steps:(a)Build a fibrous network,apply given boundary conditions and simulate the permeation of a vesicle through the elementary volume,(b)Determine the elementary time∆t,(c)Using numerical integration of the boundary of the elementary volume,compute fluxes and pressure gradients as given by(40),(41)and(43)and(d)Compute the macroscopic permeabilities using(44). The objective of this last section is to illustrate how the proposed numerical and homogenization scheme can give precious insights regarding the effect of vesicle deformability on its permeation through a fibrous network.For this,we consider the problem shown in Fig.6 and studied four quasi-random fibrous networks distinguished by similar fiber densities and distributions.For each network,we then investigate the permeation of vesicles that are characterized by a range of deformability,measured in terms of a nondimensional capillary numberCa= µV/γ.Small capillary numbers correspond to vesicles with high surface tension and low deformability;in contrast,a high capillary number reduces the solvent-vesicle surface tension and allows vesicles to undergo very large deformation and flow though narrow pores.Other parameters needed to describe the permeation of the vesicle include the non-dimensional time and permeabilities,written as: Figure 7:Vesicle speed as a function of non-dimensionalized time t∗for network 1,Ca=0.04(a)andCa=0.2(b). Figure 8:Vesicle permeability as a function of the capillary number Ca= Figure 9:Fluid permeability as a function of the capillary number Ca= Let us now turn to the macroscopic effects of these observations.For this,we compute for each network and capillary numbers the macroscopic permeabilities given in(44).For clarity,we particularly focus on understanding how the nondimensional vesicle and solvent permeabilitiesandchange as functions of the capillary numberCain Fig.8 and Fig.9 respectively.For all networks,we observe,as expected,that the vesicle permeability decreases with the capillary number,since less deformable vesicles have more difficulties squeezing through the tight pores.We also note that the vesicle permeability decreases to zero in the cases where the capillary number is low enough to cause the vesicle to be permanently trapped into the pores(fouling).On the other hand,the vesicle permeability is shown to approach that of the fluid without vesicle as the capillary number increases.Similarly,the solvent permeabilityis shown to decrease with the capillary number in Fig.9.This is explained by the fact that more rigid vesicles hinder the fluid flow through the network,and that pores can be permanently obstructed by the most rigid vesicles.More importantly,even when pores are not obstructed,Fig.9 shows that the presence of the vesicles can lessen the fluid permeability by as much as 20%for the network studied here. We have described a new numerical modeling approach that can be used to quantitatively examine the interplay between a rigid media’s structure,the surface energy of deformable,immiscible,suspended particles(vesicles),and an externally imposed continuum flow,on the particles’conductance through that media.The novelty of the approach is two-fold:(a)the inclusion of locally-explicit continuum solutions for the pressure and velocity fields that eliminate the need for the computational cost of mesh refinement and(b)the derivation of a numerical homogenization scheme that permits to calculate the macroscopic permeabilities of a fibrous network for complex fluids.We have illustrated the usefulness of the approach by performing a study on an idealized two-dimensional problem containing deformable,"cylindrical-shaped"vesicles being transported in a simple fluid through a media containing rigid flakes(which project as" fibers"in our 2-d problem).The major macroscopic figures-of-merit were the permeability coefficients of the continuous fluid and the vesicles.For the range of parameters studied,our results have illustrated that vesicles are always retarded relative to the continuum flow,and that the relative selectivity for the continuum versus the vesicle is inversely proportional to the Capillary number(based on the vesicle’s surface energy relative to the continuum fluid).Overall,these results show the capability of the proposed approach to both accurately describe the micro-scale physics of a vesicle permeation,and their effects at the macroscale in terms of effective permeability estimations.A number of improvements is however necessary to increase the fidelity of the models.First,a thorough study of the physical interaction between fibers and vesicles must be carried out.For instance,the consideration of a repulsive force between the two entities in the proposed study ultimately facilitated the flow of vesicles away from fibers.In an alternate case,where fiber-vesicle adhesion occurs,one may predict very different behaviors[De Gennes,Brochard-Wyart,and Quere(2004)].Our two-dimensional(2D)assumptions may also drastically affect the overall behavior of the system for several reasons.First,in 3D,one might expect a lower flow resistance from the fibers,but an increase in fiber- fiber connections,which might act as traps for vesicles.On the other hand,3D vesicles possess more deformation potential to escape from these obstacles.From a modeling viewpoint,the proposed computational scheme is applicable in 3D although it is not straightforward.Asympotic flows around fibers and the deformation of 3D vesicles are indeed significantly more complex than in a 2D setting,involving numerous theoretical and numerical challenges.Such research endeavors are however necessary as a fundamental undertanding of the interactions between soft vesicles and porous media can help design new membranes for medical and energy applications[Gregoriadis and Florence(1993);Allen and Cullis(2013)],but also help understand fundamental problems in biology such as the interactions between cells and their surrounding fibrous matrix[Foucard and Vernerey(2012);Vernerey and Farsad(2011);Vernerey,Foucard,and Farsad(2011)]. Acknowledgement The authors gratefully acknowledge the National Science Foundation(NSF)Industry/University Cooperative Research Center for Membrane Science,Engineering and Technology(MAST)(formerly Membrane Applied Science and Technology)at the University of Colorado at Boulder(CU-B)for their support of this research via NSF Award IIP 1034720. Appendix A: Using the spatial discretization scheme from section 3,the components of the matrix keand vector fetake the following form: whereFiandGiare the asymptotic functions used to enriched the standard finite element space around the corner tips introduced earlier. Alleborn,N.;Nandakumar,K.;Raszillier,H.;Durst,F.(1997):Further contributions on the two-dimensional flow in a sudden expansion.Journal of Fluid Mechanics,vol.330,pp.169–188. Allen,T.M.;Cullis,P.R.(2013):Liposomal drug delivery systems: from concept to clinical applications.Advanced drug delivery reviews,vol.65,no.1,pp.36–48. Baker,R.(2004):Membrane technology and applications.2nd edition. Baltus,R.E.;Badireddy,A.R.;Xu,W.;Chellam,S.(2009):Analysis of Configurational Effects on Hindered Convection of Nonspherical Bacteria and Viruses across Micro filtration Membranes.Industrial&Engineering Chemistry Research,vol.48,no.5,pp.2404–2413. Cevc,G.(2004): Lipid vesicles and other colloids as drug carriers on the skin.Advanced drug delivery reviews,vol.56,no.5,pp.675–711. Chen,Z.;Huan,G.;Ma,Y.(2006):Computational Methods for Multiphase Flows in Porous Media.SIAM. Cheryan,M.(2005):Membrane technology in the vegetable oil industry.Membrane Technology,vol.2005,no.2,pp.5–7. De Gennes,P.G.;Brochard-Wyart,F.;Quere,D.(2004):Capillarity and Wetting Phenomena.Springer. Dechadilok,P.;Deen,W.M.(2006):Hindrance Factors for Diffusion and Convection in Pores.Industrial&Engineering Chemistry Research,vol.45,no.21,pp.6953–6959. Desai,T.A.;Hansford,D.J.;Nashat,A.H.;Rasi,G.;Tu,J.;Wang,Y.;Zhang,M.;Ferrari,M.(2000):Nanopore Technology for Biomedical Applications.pp.11–40. Dillon,R.;Owen,M.;Painter,K.(2008):A single-cell-based model of multicellular growth using the immersed boundary method.Contemporary Mathematics,vol.466,no.1,pp.1–15. Eggleton,C.D.;Popel,A.S.(1998):Large deformation of red blood cell ghosts in a simple shear flow.Physics of Fluids,vol.10,no.8,pp.1834. Faibish,R.;Elimelech,M.;Cohen,Y.(1998):Effect of Interparticle Electrostatic Double Layer Interactions on Permeate Flux Decline in Cross flow Membrane Filtration of Colloidal Suspensions:An Experimental Investigation.Journal of colloid and interface science,vol.204,no.1,pp.77–86. Foucard,L.;Vernerey,F.J.(2012):A thermodynamical model for stress- fiber organization in contractile cells.Applied Physics Letters,vol.100,no.1,pp.13702–137024. Foucard,L.C.;Vernerey,F.J.(2014):An X-FEM based numerical-asymptotic expansion for simulating a Stokes flow near a sharp corner.IJNME(under review). Foucard,L.C.;Vernerey,F.J.(2014):Particle-based Moving Interface Method for the study of immersed soft vesicles.IJNME(under review),pp.1–31. Gregoriadis,G.;Florence,A.(1993): Liposomes in drug delivery.Clinical,diagnostic and ophthalmic potential.Drugs,vol.45,no.1,pp.15–28. Hawa,T.;Rusak,Z.(2002): Numerical-Asymptotic Expansion Matching for Computing a Viscous Flow Around a Sharp Expansion Corner.pp.265–281. Hoek,E.M.V.;Kim,A.S.;Elimelech,M.(2002): Influence of Cross flow Membrane Filter Geometry and Shear Rate on Colloidal Fouling in Reverse Osmosis and Nanofiltration Separations.Environmental Engineering Science,vol.19,no.6,pp.357–372. Jason,H.;Kumar,T.(2012):Advances in Computational Dynamics of Particles,Materials and Structures.John Wiley&Sons,Ltd. Leung,S.;Lowengrub,J.;Zhao,H.(2011):A Grid Based Particle Method for Solving Partial Differential Equations on Evolving Surfaces and Modeling High Order Geometrical Motion.Journal of Computational Physics,vol.230,no.7,pp.2540–2561. Leung,S.;Zhao,H.(2009):A grid based particle method for moving interface problems.Journal of Computational Physics,vol.228,no.8,pp.2993–3024. Li,Y.;Yun,A.;Kim,J.(2011):An immersed boundary method for simulating a single axisymmetric cell growth and division.Journal of mathematical biology,vol.65,no.4,pp.653–675. Ma,L.;Klug,W.S.(2008):Viscous regularization and r-adaptive remeshing for finite element analysis of lipid membrane mechanics.Journal of Computational Physics,vol.227,no.11,pp.5816–5835. Moës,N.;Dolbow,J.;Belytschko,T.(1999): A finite element method for crack growth without remeshing.International Journal for Numerical Methods in Engineering,vol.46,no.1,pp.131–150. Moffatt,H.K.(1963):Viscous and resistive eddies near a sharp corner.vol.18,pp.1–18. Mullin,T.;Seddon,J.R.T.;Mantle,M.D.;Sederman,a.J.(2009):Bifurcation phenomena in the flow through a sudden expansion in a circular pipe.Physics of Fluids,vol.21,no.1,pp.014110. Peskin,C.(1972): Flow patterns around heart valves:A numerical method.Journal of Computational Physics,vol.10,no.2,pp.252–271. Rabczuk,T.;Gracie,R.;Hsong,J.;Belytschko,T.(2000):Immersed Particle Method for Fluid-Structure Interaction.pp.1–6. Song,L.(1998): Flux decline in cross flow micro filtration and ultra filtration:mechanisms and modeling of membrane fouling.Journal of Membrane Science,vol.139,no.2,pp.183–200. Vernerey,F.;Liu,W.K.;Moran,B.(2007):Multi-scale micromorphic theory for hierarchical materials.Journal of the Mechanics and Physics of Solids,vol.55,no.12,pp.2603–2651. Vernerey,F.J.(2011):A theoretical treatment on the mechanics of interfaces in deformable porous media.International Journal of Solids and Structures,vol.48,no.22-23,pp.3129–3141. Vernerey,F.J.(2012): The Effective Permeability of Cracks and Interfaces in Porous Media.Transport in Porous Media,vol.93,no.3,pp.815–829. Vernerey,F.J.;Farsad,M.(2011):A constrained mixture approach to mechanosensing and force generation in contractile cells.Journal of the mechanical behavior of biomedical materials,vol.4,no.8,pp.1683–99. Vernerey,F.J.;Foucard,L.;Farsad,M.(2011):Bridging the Scales to Explore Cellular Adaptation and Remodeling.BioNanoScience,vol.1,no.3,pp.110–115. Zhang,L.;Gerstenberger,A.;Wang,X.(2002): Immersed Finite Element Method.Computer Methods in Applied Mechanics and Engineering,,no.September 2003,pp.1–25.3.3 Grid based particle method for interface evolution

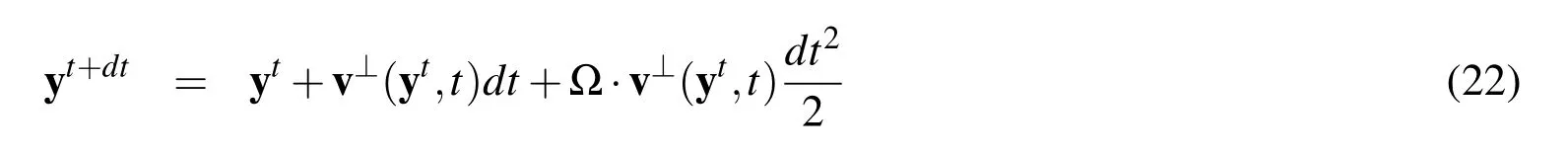
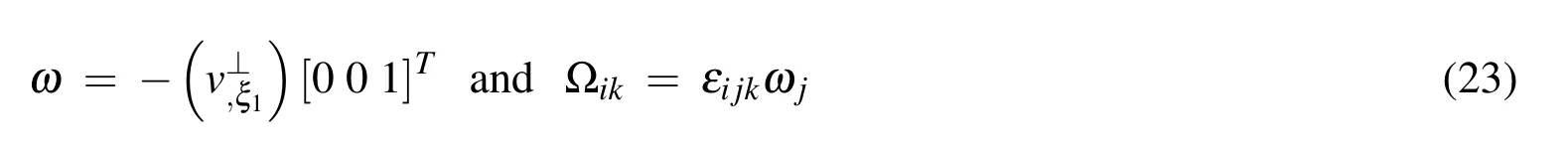



3.4 Validation for the pressure/velocity field in the tip vicinity

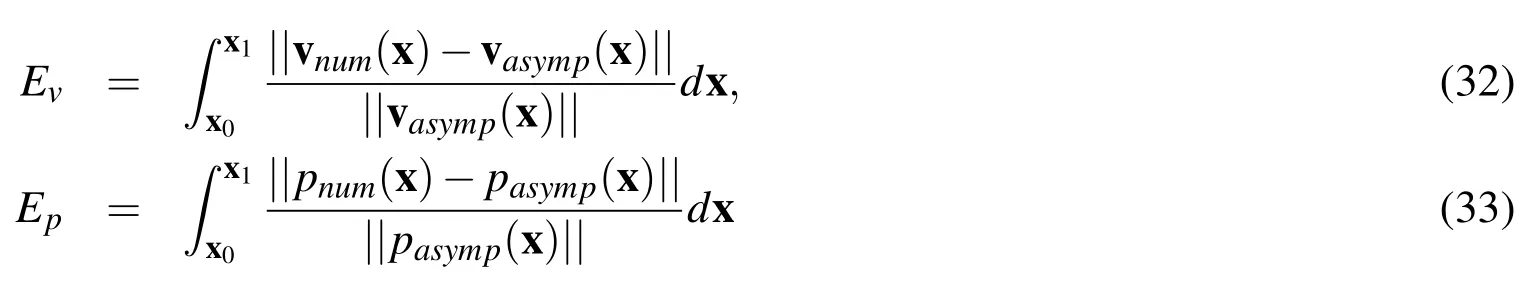

4 Numerical approach to predict the permeation of a soft colloids though a fibrous network
4.1 General homogenization scheme to compute macroscopic permeabilities


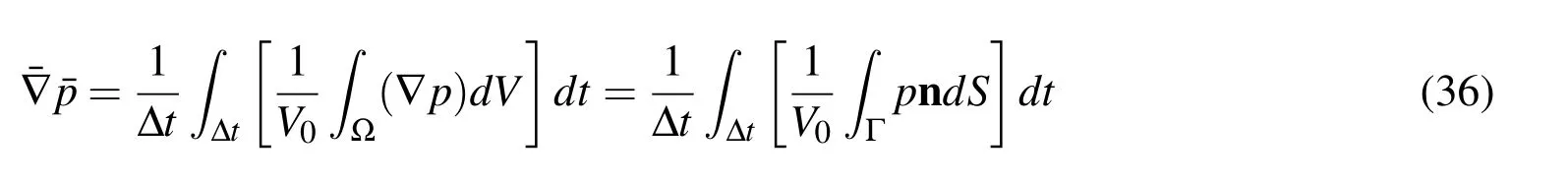

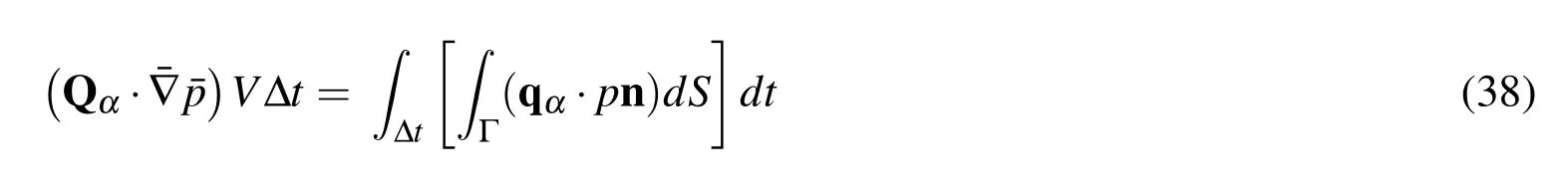

4.2 Application to the numerical evaluation of the permeation of soft colloidal particles
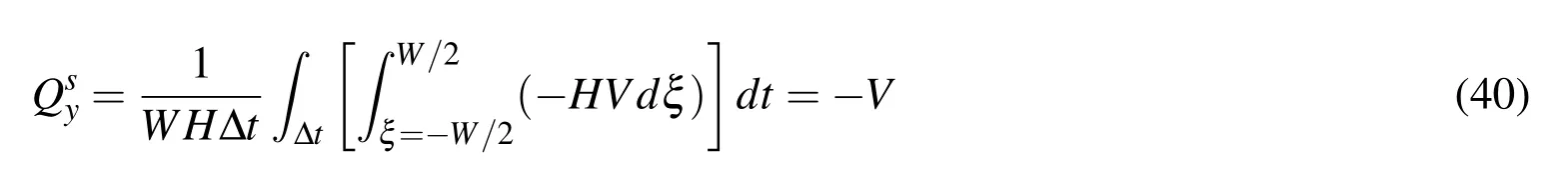


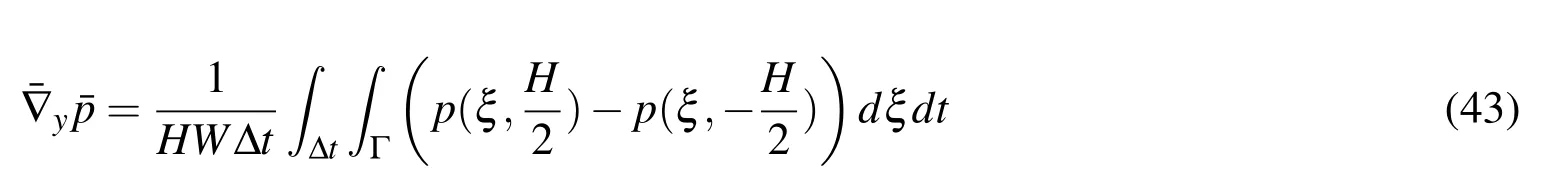
4.3 Numerical investigation of the role of surface tension soft vesicles permeation
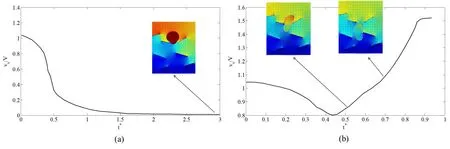

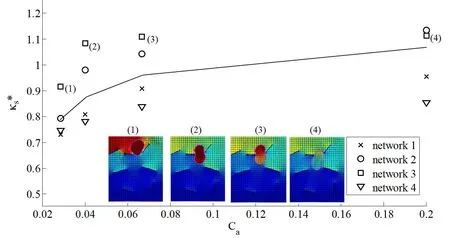
5 Summary and future work


 Computer Modeling In Engineering&Sciences2014年7期
Computer Modeling In Engineering&Sciences2014年7期
- Computer Modeling In Engineering&Sciences的其它文章
- A Meshfree Method For Mechanics and Conformational Change of Proteins and Their Assemblies
- Simulations of Blood Drop Spreading and Impact for Bloodstain Pattern Analysis
- Large Deformation Dynamic Three-Dimensional Coupled Finite Element Analysis of Soft Biological Tissues Treated as Biphasic Porous Media
- Preface
