Composite Simpson’s Rule for Computing Supersingular Integral on Circle

Jin LiHongxing Ru and Dehao Yu

1 Introduction

In this paper we consider the following supersingular integral on the circle

Following the definition of Hadamard finite-part integral,we have

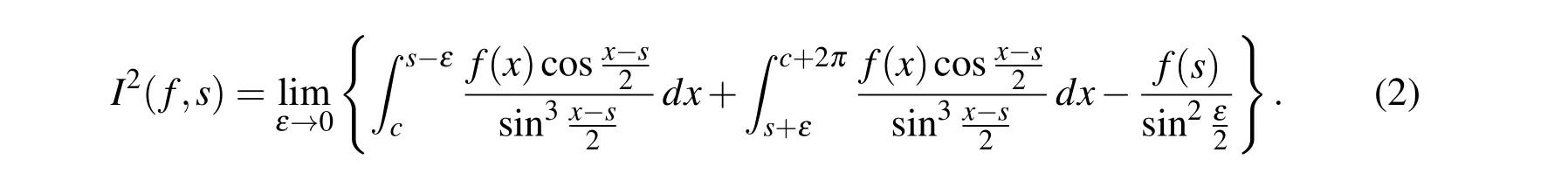
The error analysis for Riemann integrals with the composite Simpson rule has been well done.The convergence rate for the usual Riemann integrals isO(h4).However,it is not true for Hadamard finite-part integrals due to the hypersingularity of the integrand.The Newton-Cotes methods for computation the hypersingular integral on interval was studied by[Linz(1985)].Then in 1993,[Yu(1993)]gave a new quadrature formulae to compute the case of singular point coinciding with the mesh point which presented the error estimate isO(h|lnh|).In recent years,a modified trapezoidal rule was presented by[Wu and Yu(1999)]and the convergence rate is proved.Numerical methods have been extensively investigated for hypersingular integral on the interval[Abdou(2003);Akel and HusseinH(2011);Chen and Hong(1999);Klerk(2002);Monegato(1994);Zhou Li and Yu(2010);Choi,Kim,and Yun(2004);Hasegawa(2004);Hui and Shia(1999);Ioakimidis(1985);Kim and Jinn(2002);Li Wu and Yu(2009);Li and Yu(2011a,b);Li Zhang and Yu(2013);Zhou Li and Yu(2010)].

The Simpson rule for the computation of supersingular integral on interval was firstly discussed in[Du(2001)]and theO(h)convergence rate is proved,then in the year of 2005,the trapezoidal rule for supersingular integral was presented in[Wu and Sun(2005)]where this rule was shown to be divergent in general,but exhibit the superconvergence phenomenon at certain special point.Then[Zhang,Wu and Yu(2009)],the superconvergence phenomenon of the composite Simpson��s rule for the supersingular was studied and the superconvergence estimate was given.In recent paper[Li Zhang and Yu(2010)],the general Newton-Cotes rules for evaluating the supersingular integrals were investigated and the error expansion estimate of the Newton-Cotes rules were obtained.

The hypersingular integral in circle have not been studied widely,maybe reference[Yang(2013);Zhang,Wu and Yu(2010,2009)]cover the whole area.In this paper,based on the error expansion of the density function,the error functional of the supersingular integral is obtained.We are concerning with the pointwise superconvergence phenomenon,i.e.,when the singular pointscoincides with some a priori known points,the convergence rate of the composite Simpson rule is higher than what is globally possible.We show that a convergence rate can reachO(h2)with the local coordinate equal to zero which depends upon the regularity of the density function.

The rest of this paper is organized as follows.In Sect.2,after introducing some basic formulas of the general(composite)Simpson rule and notations,we present our main result.In Sect.3 the corresponding theoretical analysis is given.Finally,several numerical examples are given to validate our analysis.

2 Main result

Letc=x0＜x1＜···＜xn-1＜xn=c+2πbe a uniform partition of the interval[c,c+2π]with mesh sizeh=2π/nandfQ(x)be defined as the Simpson interpolation forf(x)andxi=c+(i-1)h,xi-1/2=xi-h/2,with basis function defined as below

We also define a linear transformation

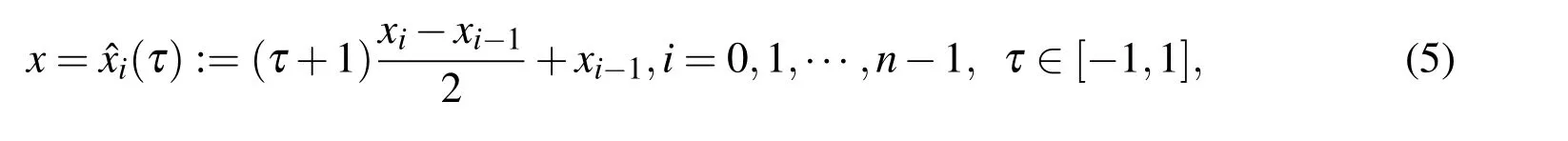
from the reference element[-1,1]to the subinterval[xi-1,xi].

The new composite Simpson rule is given byfQ(x)to replacingf(x)in Eq.1

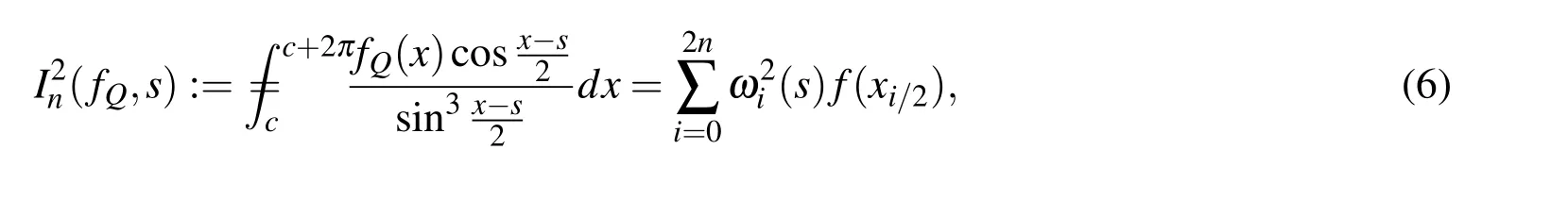
By straightly calculation,we have

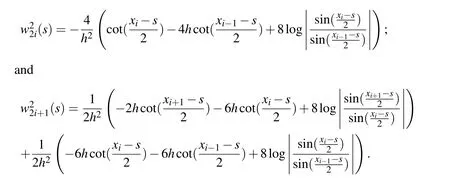
Now we present our main results below.The proof will be given in next section.

Theorem 1Assume f(x)∈C4[c,c+2π].For the Simpson rule In(f,s)defined in Eq.6,there exists a positive constant C,independent of h and s such that

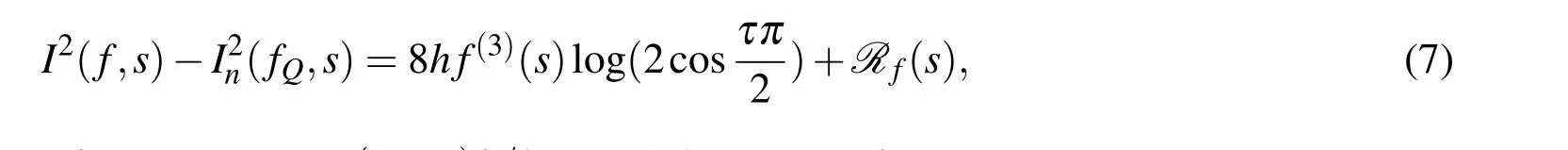
where s=xm-1+(1+τ)h/2,m=1,2,···,n and

In the following,Cwill denote a generic constant which is independent ofhandsand may have different values in different places.In addition,we assume thats∈(xm-1,xm),for somemand lets=xm-1+(τ+1)h/2 withτ∈(-1,1)denoting its local coordinate.

Now we defineI n,i(s)as below

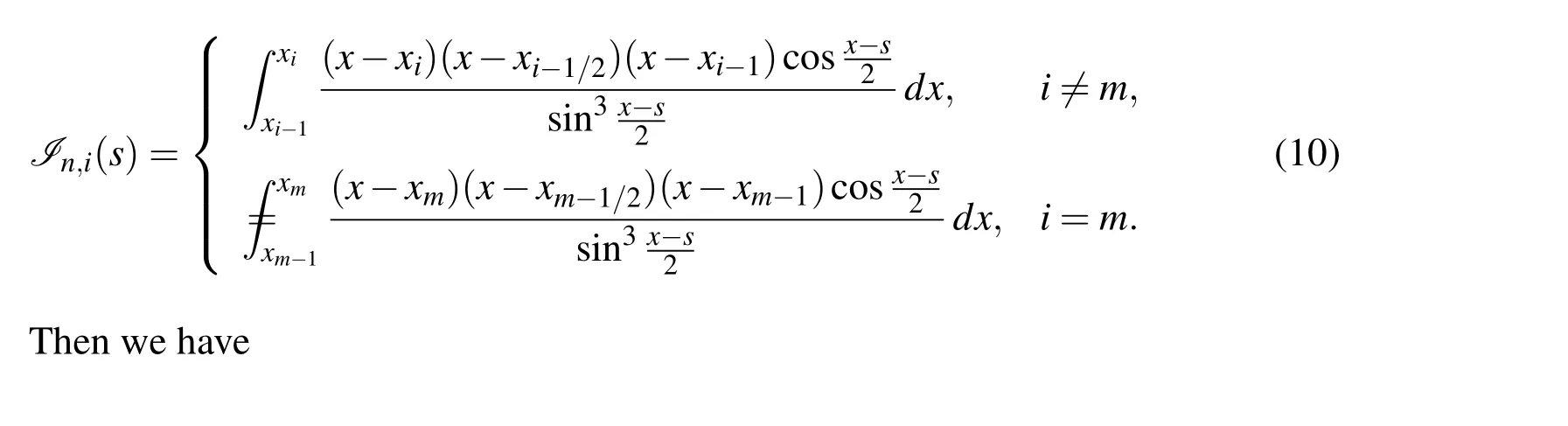
Lemma 1Assume s=xm-1+(τ+1)h/2with τ∈(-1,1).Let I n,i(s)be defined by(10).Then there holds that

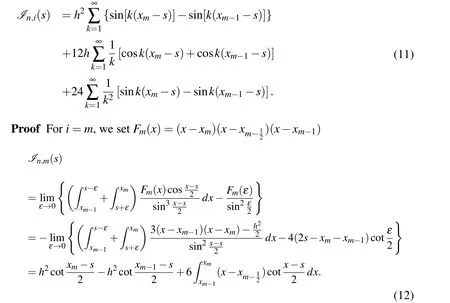
Similarly,fori/=m,using integral by parts on the corresponding Riemann integral,we have

Now,by using the well-known identity(see,e.g.,[Andrews(2002);Yu(2002)]),

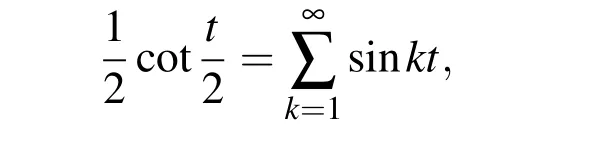
we can easily obtain(11)from(12)and(13).□

Lemma 2Under the same assumptions of Lemma 1,there holds that

ProofBy(11),we have

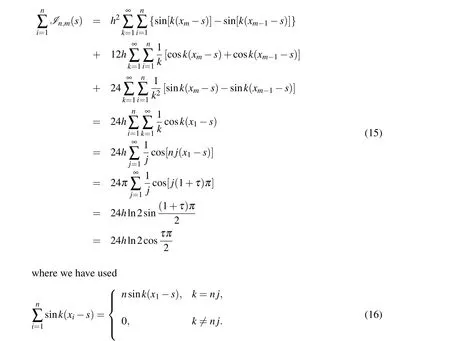
The proof of Lemma 2 is completed. □

Before presenting the main results,we firstly defineKs(x)

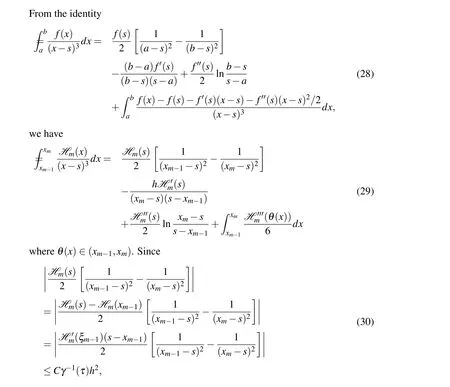
Lemma 3Assume that f(x)∈C4[a,b]and fQ(x)be defined by Eq.3,there holds

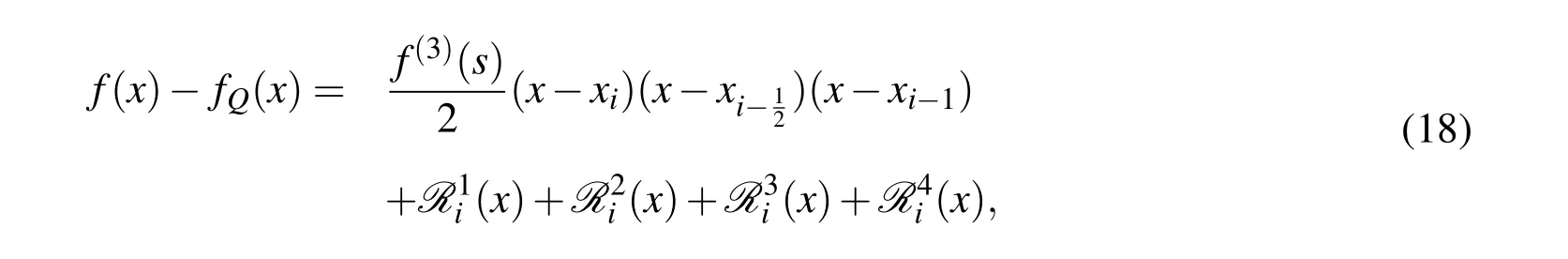
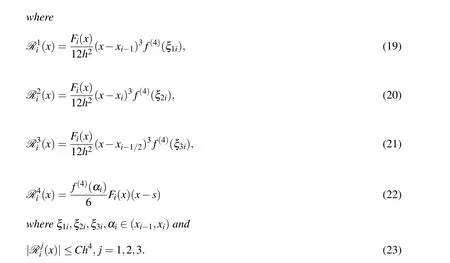
By performingf(xi),f(xi-1/2),f(xi-1)at the pointx,the proof can is similarly as in reference[Li Zhang and Yu(2010)].□

Setting

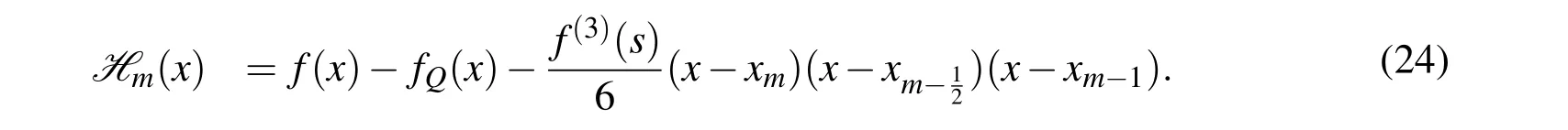
Lemma 4Under the same assumptions of Theorem 1,for H m(x)in Eq.24,there holds that

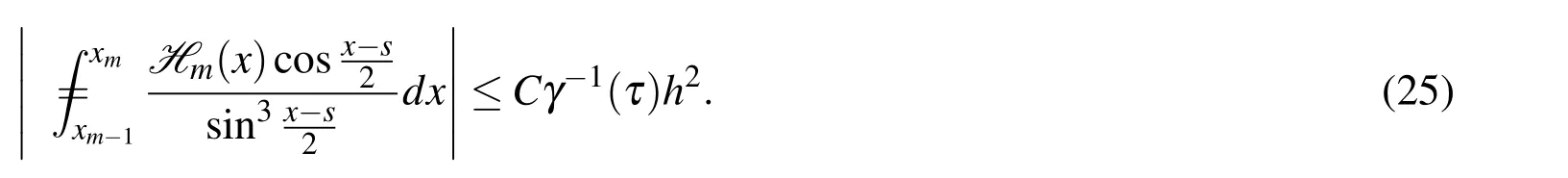
where γ(τ)is defined in Eq.9.

Proof.By the definition ofH m(x),we have

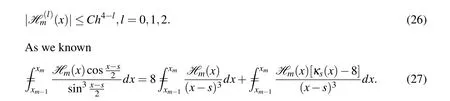
whereξm-1∈(xm-1,xm)and we have usedH m(xm-1)=0.

Then we have

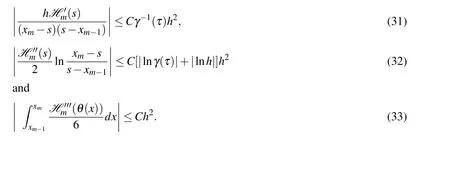
As for the second term,

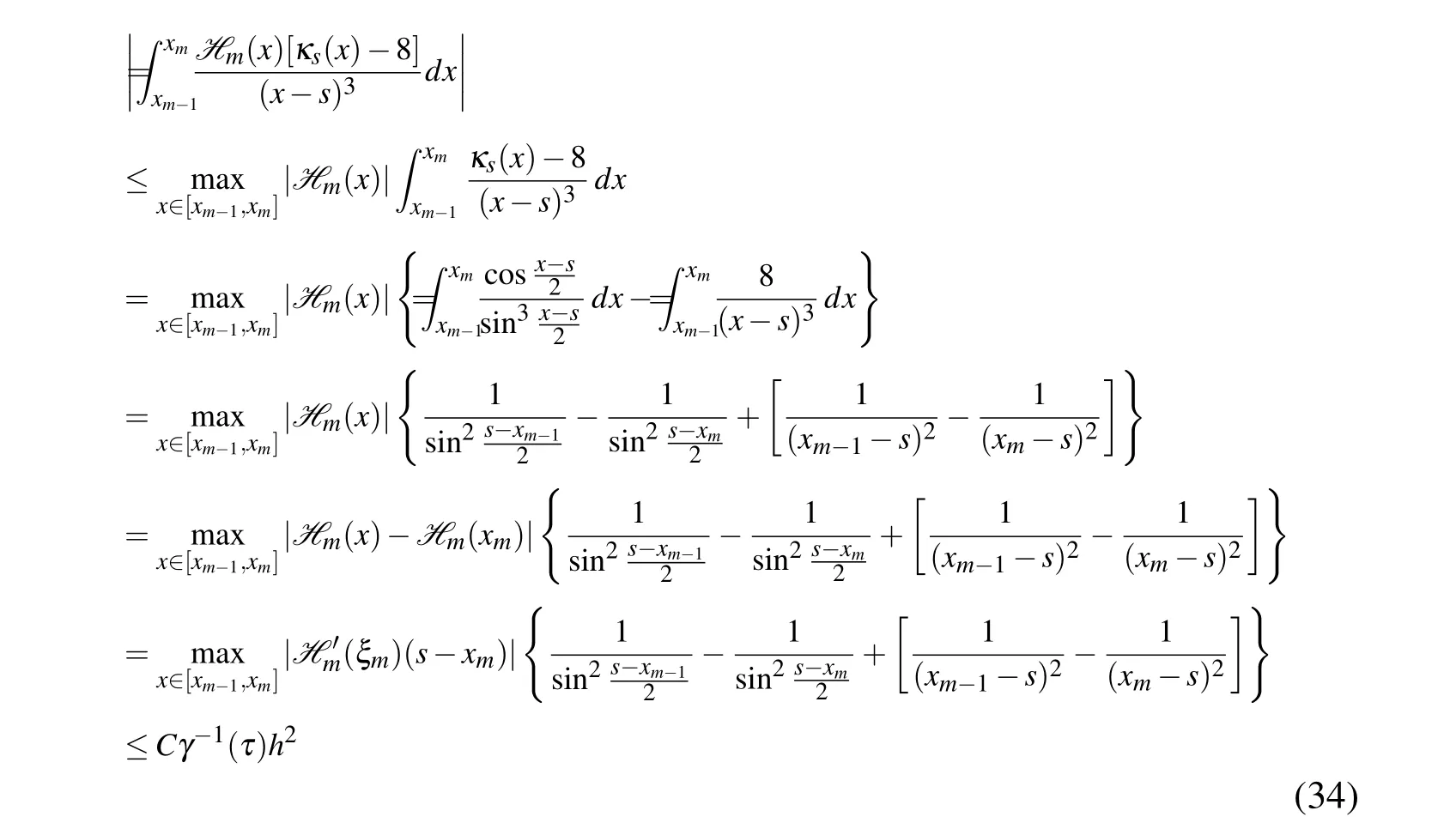
Eq.25 can be obtained by putting together from Eq.29 to Eq.34 which completes the proof.□

The proof of Theorem 1:According to Eq.24,we have

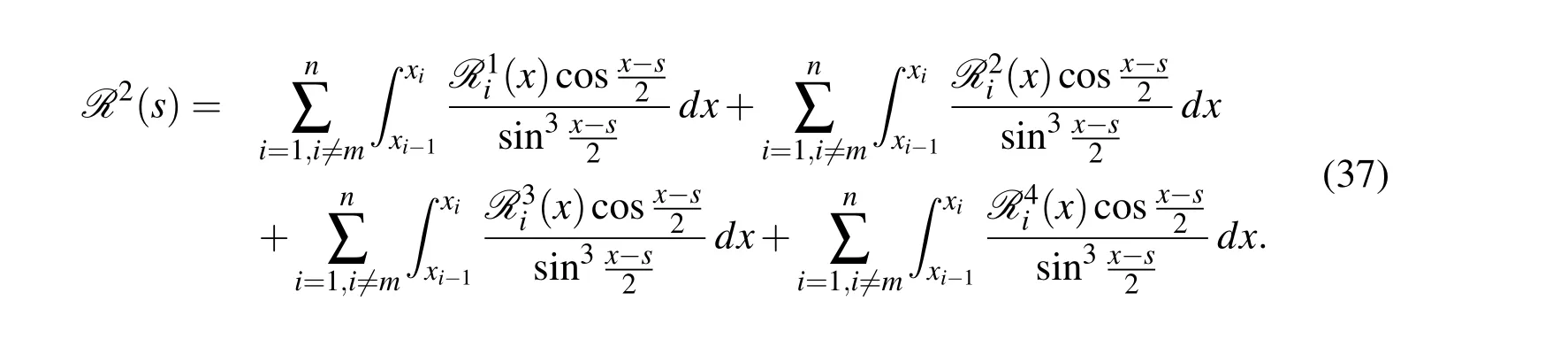
For the first part of Eq.37,we have

For the second part of Eq.37,we have

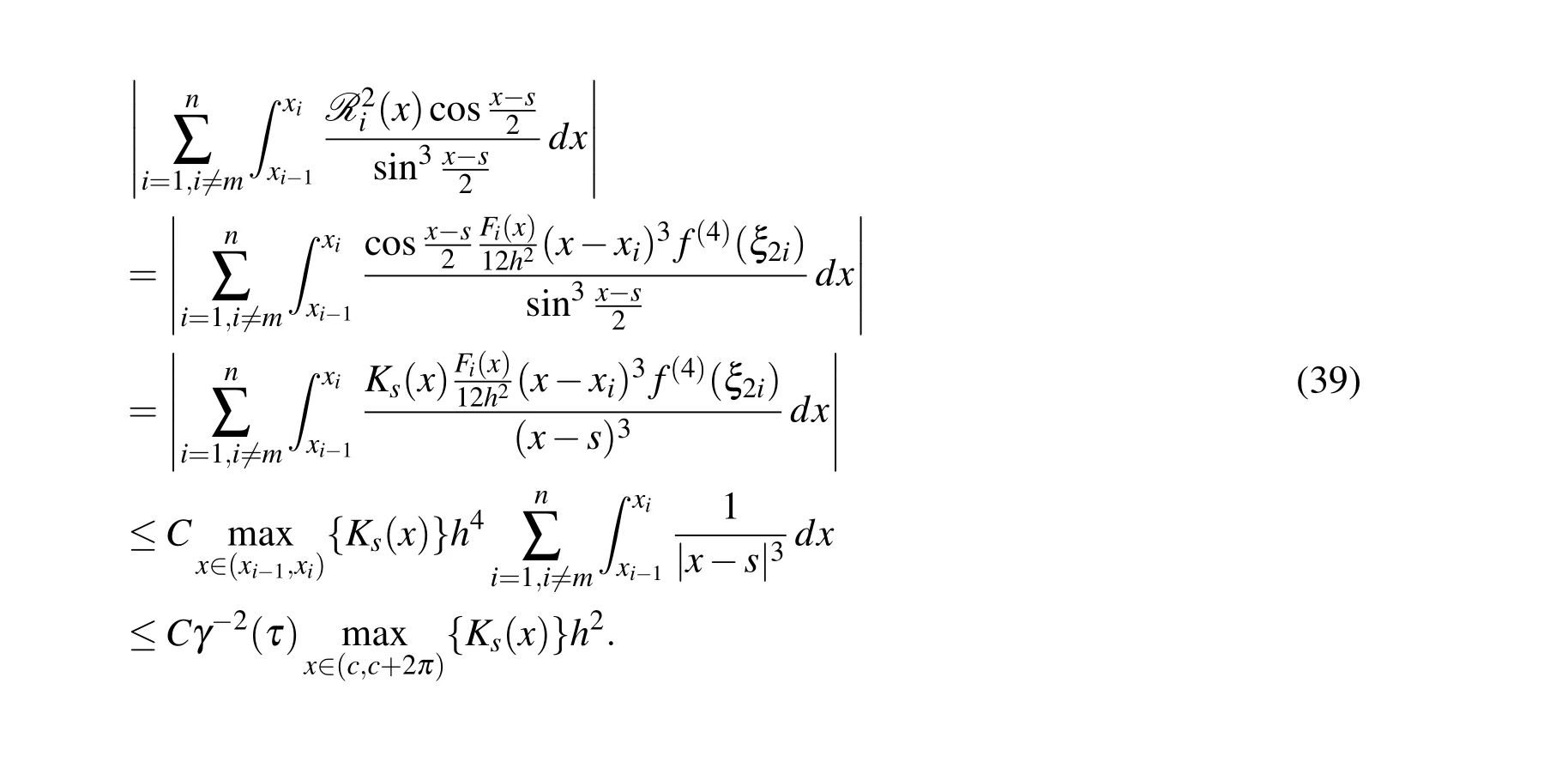
For the third part of Eq.37,we have

From Eq.38 to Eq.41 and Lemma 4,we have

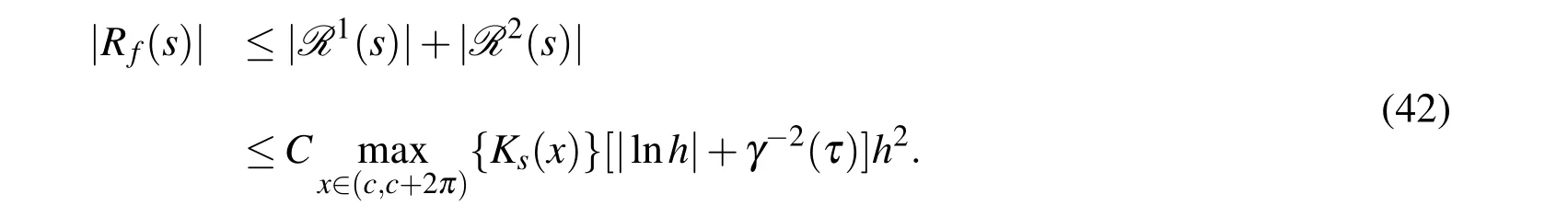
Then the proof is completed.□

From the above analysis,we obtain the following modify Simpson rule,

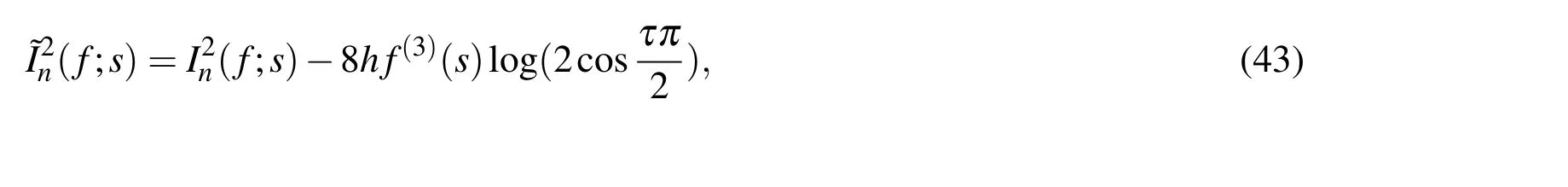
Based on the theorem 1,we present the modify Simpson rule

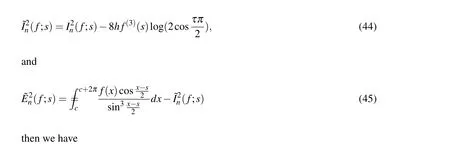
Corollary 1Under the same assumption of theorem 1,we have

where γ(τ)is defined as Eq.9.

The above equation implies that,for the finite part integral Eq.1,the composite Simpson rule can reach the convergencerateO(h)in general.While for the error

3 Numerical example

In this section,computational results are reported to confirm our theoretical analysis.

Example 1Consider the supersingular integral

with f(x)=1+sin(x)+cos(x)and the exact analysis is4π[sin(s)-cos(s)]

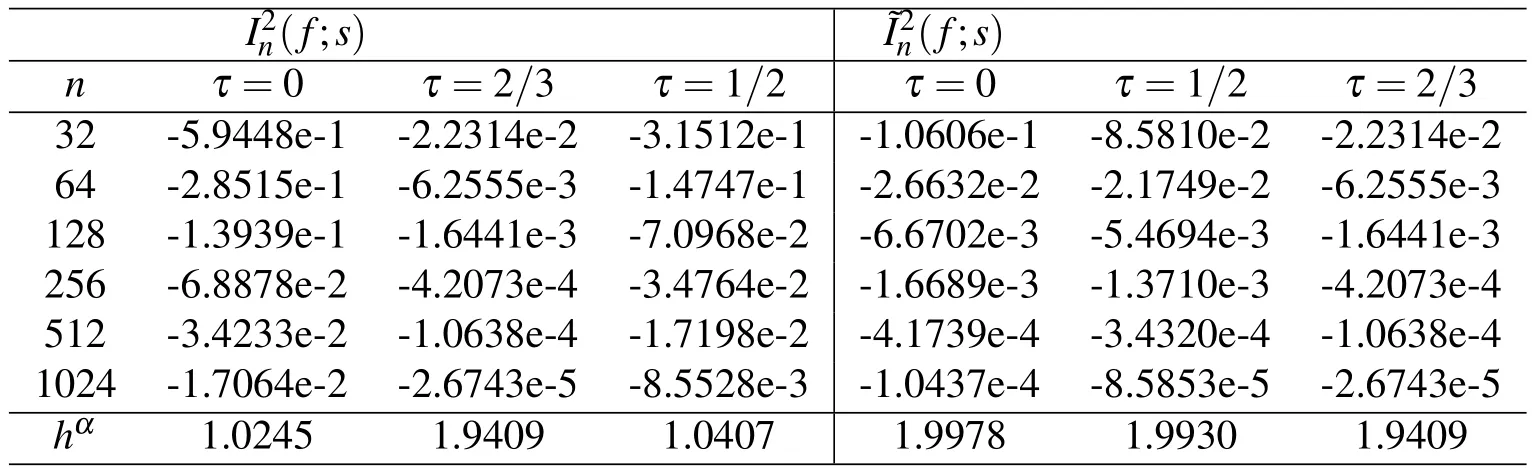
Table 1:Errors of the Simpson rule and mod-Simpson rule s=a+x[n/4]+(1+τ)h/2

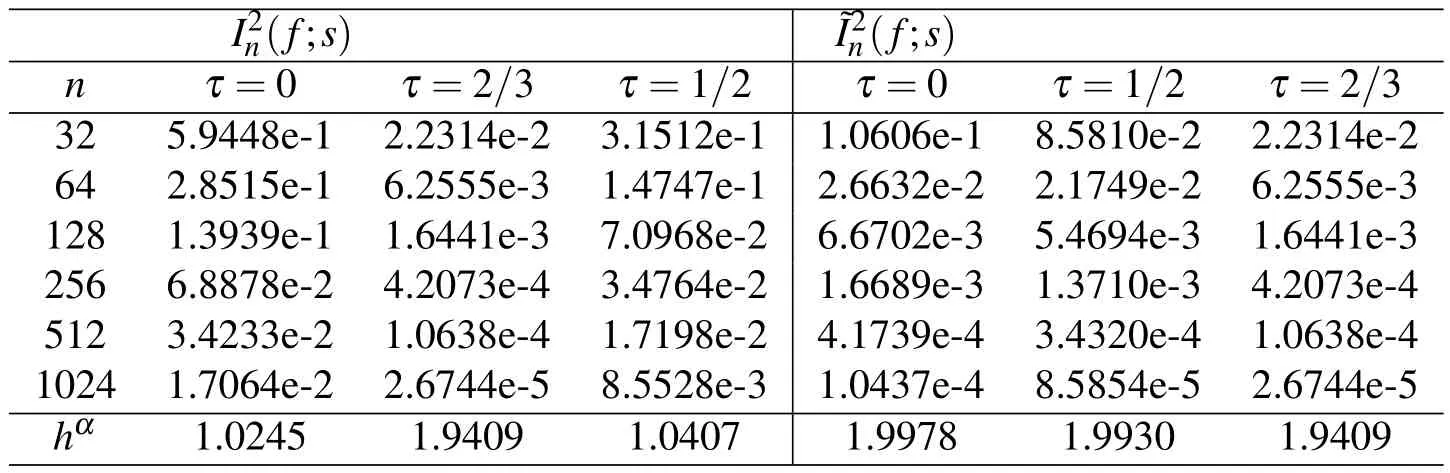
Table 2:Errors of the Simpson rule and mod-Simpson rule s=b-(1+τ)h/2

Table 3:Errors of the Simpson rule and mod-Simpson rule s=a+(1+τ)h/2

Example 2Consider the supersingular integral

as for the non-supersingular point the the convergence rate is O(h)which agree with our theorematically analysis.From the modify Simpson rule the table 4 shows the convergence rate of is O(h3)at the non-superconvergence point which coincide with our Corollary 1.For the case of s=b-(1+τ)h/2,table 5 and 6 show that the convergence rate of O(h2)for the superconvergence point no influence of the boundary condition which coincide with our theoretically analysis while for the modify Simpson rule the convergence rate can reach O(h2)which agree our Corollary 1.

Table 4:Errors of the Simpson rule and mod-Simpson rule s=a+x[n/4]+(1+τ)h/2

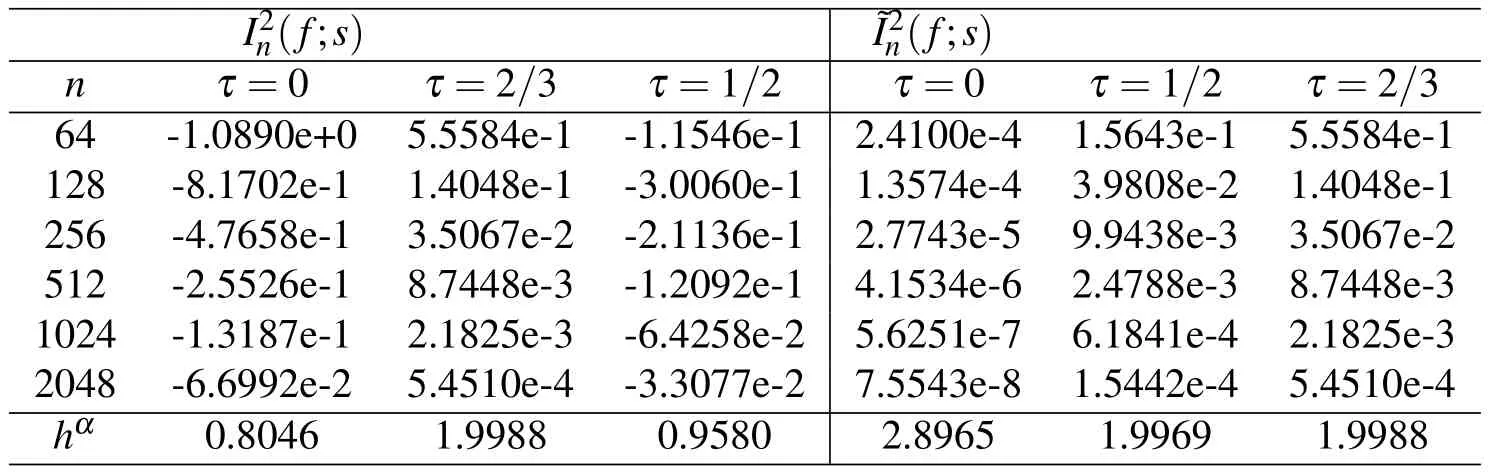
Table 5:Errors of the Simpson rule and mod-Simpson rule s=b-(1+τ)h/2

4 Conclusion

In this paper,we study the composite Simpson’s rule for numerical evaluation supersingular integrals defined on circle.Based on the error expansion in each subinterval,the superconvergence phenomenon is obtained.The results in this paper show a possible way to improve the accuracy of the collocation method for supersingular integral equations by choosing the superconvergence points to be the collocation points.

Acknowledgment

The work of Li Jin was supported by National Natural Science Foundation of China(No.11101247,No.11201209 and No.91330106),China Postdoctoral Science Foundation(No.2013M540541)and the Shandong Provincial Natural Science Foundation of China(No.ZR2011AQ020).The work of Hongxing Rui was supported by National Natural Science Foundation of China(No.91330106).

Andrews,L.C.(2002):Special Functions of Mathematics for Engineers.McGraw-Hill,Inc.

Abdou,M.A.(2003): Fredholm-Volterra integral equation with singular kernel.Appl.Math.Comput.,vol.137,pp.231-243.

Akel,M.HusseinH.(2011): Numerical treatment of solving singular integral equations by using Sinc approximations.Appl.Math.Comput.,vol.218 pp.3565-3573.

Chen,J.T.;Hong,H.K.(1999): Review of dual boundary element methods with emphasis on hypersingular integrals and divergent series,Applied Mechanics Reviews,ASME,vol.52,no.1,pp.17-33.

Choi,U.J.;Kim,S.W.;Yun,B.I.(2004): Improvement of the asymptotic behaviour of the Euler-Maclaurin formula for Cauchy principal value and Hadamard finite-part integrals.Int.J.Numer.Methods.,vol.61,pp.496-513.

Du,Q.K.(2001):Evaluations of certain hypersingular integrals on interval.Int.J.Numer.Methods.,vol.512,pp.1195-1210.

Hasegawa,T.(2004):Uniform approximations to finite Hilbert transform and its derivative,J.Comput.Appl.Math.,vol.163,pp.127-138.

Hui,C.Y.;Shia,D.(1999):Evaluations of hypersingular integrals using Gaussian quadrature.Int.J.Numer.Methods.,vol.44,pp.205-214.

Ioakimidis,N.I.(1985):On the uniform convergence of Gaussian quadrature rules for Cauchy principal value integrals and their derivatives.Math.Comp.,vol 44,pp.191-198.

Kim,P.;Jin,U.C.(2003): Two trigonometric quadrature formulae for evaluating hypersingular integrals.Inter,Inter.J.Numer.Methods Eng.,vol.56,pp.469-486.

Klerk,J.(2002):Solving strongly singular integral equations by Lp approximation methods.Appl.Math.Comput.,vol.127,pp.311-326.

Li.J;Wu,J.M;Yu,D.H.(2009): Generalized extrapolation for computation of hypersingular integrals in boundary element methods.CMES:Computer Modeling in Engineering&Sciences,vol.42,no.2,pp.151-175.

Li,J.;Yu,D.H.(2011): The Superconvergence of Certain Two-Dimensional Cauchy Principal Value Integrals.CMES:Computer Modeling in Engineering&Sciences,vol.71,no.4,pp.331-346.

Li,J.;Yu,D.H.(2011): The Superconvergence of Certain Two-Dimensional Hilbert singular Integrals.CMES:Computer Modeling in Engineering&Sciences,vol.84,no.4,pp.233-252.

Li.J;Zhang X.P.;Yu,D.H.(2010): Superconvergence and ultraconvergence of Newton-Cotes rules for supersingular integrals.J.Comput.Appl.Math.,vol.233,no.11,pp.2841-2854.

Li.J;Zhang X.P.;Yu,D.H.(2013): Extrapolation methods to compute hypersingular integral in boundary element methods.Science China Mathematics,vol.56,no.8,pp.1647-1660.

Linz,P.(1985): On the approximate computation of certain strongly singular integrals.Computing,vol.35,pp.345-353.

Monegato,G.(1994): Numerical evaluation of hypersingular integrals.J.Comput.Appl.Math.vol.50.pp.9-31

Yu,D.H.(2002):Natural Boundary Integrals Method and its Applications.K-luwer Academic Publishers.

Yu,D.H.(1993):Mathematical Theory of Natural Boundary Element Method.Science Press,Beijing.

Wu,J.M.;Yu,D.H.(1999):The approximate computation of hypersingular integrals on interval.Chinese J.Numer.Math.Appl.,vol.21 pp.25-33.

Wu,J.M.;Sun,W.W.(2005):The superconvergence of the composite trapezoidal rule for Hadamard finite part integrals.Numer.Math.,vol.102,pp.343–363.

Yang,C.X(2013): A unified approach with spectral convergence for the evaluation of hypersingular and supersingular integrals with a periodic kernel.J.Comput.Appl.Math.,vol.239,pp.322-332.

Zhang,X.P.,Wu,J.M.,Yu,D.H.(2009):Superconvergence of the composite Simpsons rule for a certain finite-part integral and its applications,.,J.Comput.Appl.Math,vol.223 pp.598-613.

Zhang,X.P.,Wu,J.M.,Yu,D.H.(2010):The Superconvergence of composite trapezoidal rule for Hadamard finite-part integral on a circle and its application.,Inter J Comput Mathvol.87,pp.855-876

Zhang,X.P.,Wu,J.M.,Yu,D.H.(2009):The superconvergence of composite Newton-Cotes rules for Hadamard finite-part integral on a circle.,Computingvol.85,pp.219-244.

Zhou,Y.T.Li,J.Yu,D.H.,(2010): Numerical solution of hypersingular equation using recursive wavelet on invariant set.Appl.Math.Comput.,vol.217,pp.861-868.