楔形离合器系统的正压力观测
余孟珂姚 健陈 俐
(1.上海交通大学;2.上海交通大学 汽车电子控制技术国家工程实验室)
1 前言
楔形离合器的正压力值可以预测汽车的传动系统动力学特性,并在此基础上设计合适的控制策略以提高汽车传动系统品质;同时,正压力值随系统输入电流变化情况是判断离合器是否有效工作的重要手段。在实验室环境下可用力传感器实时测量正压力值,但该方法有两个缺陷:第一,在整车设计时,离合器所在区域没有足够的空间安装力传感器;第二,汽车工业对成本控制十分严格,精确的力传感器往往价格不菲,这制约了其实际运用。本文通过为楔形离合器系统建立状态观测器实时预测正压力输出值。常见的状态观测方法有龙伯格状态观测器[1,2]、卡尔曼滤波器[3~5]以及滑模观测[6,7]。 卡 尔 曼 滤 波器因其能够充分考虑到系统过程噪声和测量噪声对观测的影响,对于汽车离合器这一受噪声影响的系统最为适用。
首先在楔形离合器系统物理学原理基础上建立状态空间描述,其次建立了适用于本系统的卡尔曼滤波器,并通过试验测试了卡尔曼滤波器的估计性能。
2 楔形离合器系统的原理分析与状态空间
2.1 楔形离合器系统的动力学模型
如图1所示,楔形离合器系统从原理上分为5部分,分别是作为输入装置的直流无刷电机部分、连接轴部分、蜗轮蜗杆部分、楔形机构部分以及离合器组件。
电机与负载、阻尼之间的动力学关系如下:
式中,I为电流;Tm为力矩;Ta为施加给连接轴的转矩;Jm0是电机的等效转动惯量;θ0是电机转轴的角位移;C0是电机内等效阻尼系数。
连接轴是一根弹性系数为K1的弹簧,用θ0和θw分别代表电机和蜗杆的旋转角位移,可得弹力力矩的表达式为:
蜗杆与连接轴相连,另一端通过齿轮比为n的齿轮带动涡轮旋转,如公式(4)所示;涡轮与楔形机构啮合,并给楔形机构施加旋转力矩,蜗轮蜗杆的动力学方程如公式(5)所示。
式中,θ1和Jm1分别代表涡轮的角位移和等效转动惯量;C1是蜗轮蜗杆的等效阻尼系数。
楔形机构由固定在旋转盘圆周上的楔形块和固定在离合器外壳上的支点组成,楔形块与涡轮啮合,另一端与离合器压力盘之间有一段长度为x20的间隙。当楔形块发生角位移θ2时,受到支点的反作用力Fz,并产生轴向位移X2。楔形块与涡轮同轴转动,得到公式(6):
有:
式中,α是楔块斜面的倾角;Rw是楔形块所在旋转盘的等效半径。
楔形块转动和轴向运动的动力学方程为:
式中,Jm2为楔形块的转动惯量;Tb是楔形机构和摩擦盘之间的摩擦力矩;C2是楔形机构旋转方向上的等效阻尼;C3是轴向运动的等效阻尼;Mm2是楔形机构整体等效质量;Fn是离合器片对楔形机构轴向的反作用力。
离合器组件由压盘和离合器片组成,压盘一端连接楔形机构,另一端连接离合器片。离合器片可以被简化为一段弹性系数为K2的弹簧:
离合器压盘所产生的摩擦力矩可以看做两种模式,滑动模式如公式(12)所示,静止模式如公式(13)所示。
2.2 楔形离合器系统的状态空间表达
当X2<x20时离合器未发生接合作用,正压力Fn=0,此时压力对汽车传动系统的研究没有价值。在楔形离合器研究中,更具有实用价值的过程是楔形机构和离合器发生作用之后产生的主要驱动力的变化情况,所以本文主要研究离合器的接合特性,即X2≥x20时的系统特性。
选取整个楔形离合器的系统状态为:
其中,θ0为直流无刷电机转角。
本文选用电机转角作为系统测量值,记为测量值z,测量矩阵为:
可得系统测量方程为:
将电流I作为系统输入,当x4>θ20时系统的状态空间描述如公式(17)所示:
其中,H如公式(15)所示,F、B和C分别如公式(18)~公式(20)所示:
2.3 楔形离合器系统的稳定性与能观性
根据现代系统理论[8,9],对于公式(17)描述的线性定常系统,其渐近稳定的充分必要条件是F的所有特征值具有负实部,因此对系统稳定性的判断可以由求解的特征值来解决。在Matlab中使用命令函数eig求解F的特征值为:
可见状态矩阵F的4个特征值全部具有负实部,在这些条件下系统稳定。
对于公式(17)所示的系统,能观性判别矩阵如公式(23)所示:
在Matlab中求得rankQ=4,判别矩阵满秩,该系统能观。
3 卡尔曼滤波器
根据卡尔曼滤波器理论,系统的状态空间表达如公式(24)和公式(25)所示:
式中,X是系统状态向量;U是系统输入;F是系统状态矩阵;B是输入矩阵;ω是系统的过程噪声,且是协方差为Q的高斯白噪声;z是测量值向量;H是测量矩阵;v是测量噪声,且是协方差为R的白噪声。
假设T为测量的采样时间,对于线性时不变系统,在采样周期T小于系统最小时间常数的时[8,9],离散状态矩阵为:
因此,卡尔曼滤波理论状态空间描述的离散形式如公式(28)和(29)所示:
则可以得到如公式(30)所示的卡尔曼滤波器,该公式可以由公式(31)~公式(35)递归运算得到。
Pk是每次估计值更新后误差的协方差,假设噪声ω和v之间相互独立,即满足公式(37):
假设测量噪声 vk~N(0,R),且 R=2×10-4,则系统估计误差的协方差初始值为P0:
根据上述参数即可以建立卡尔曼滤波器的主要结构。
4 卡尔曼滤波器估计性能的试验验证
试验中,实际的楔形离合器系统输入信号为I,输出为压力传感器的测量值Fn(k);卡尔曼滤波器接受两个输入信号,分别是与楔形离合器相同的系统输入Ik及直流无刷电机角度传感器的测量值θ0(k),给出相同时刻离合器受到的正压力值估计值F^n(N)。试验中电机角位移器的测量值θ0(k)和离合器正压力的测量值序列Fn(k)均以Tp=0.01s为周期给出。试验目的是比较卡尔曼滤波器正压力估计值F^n(N)与压力传感器测量值Fn(k)。试验中用到的物理参数如表1所示。
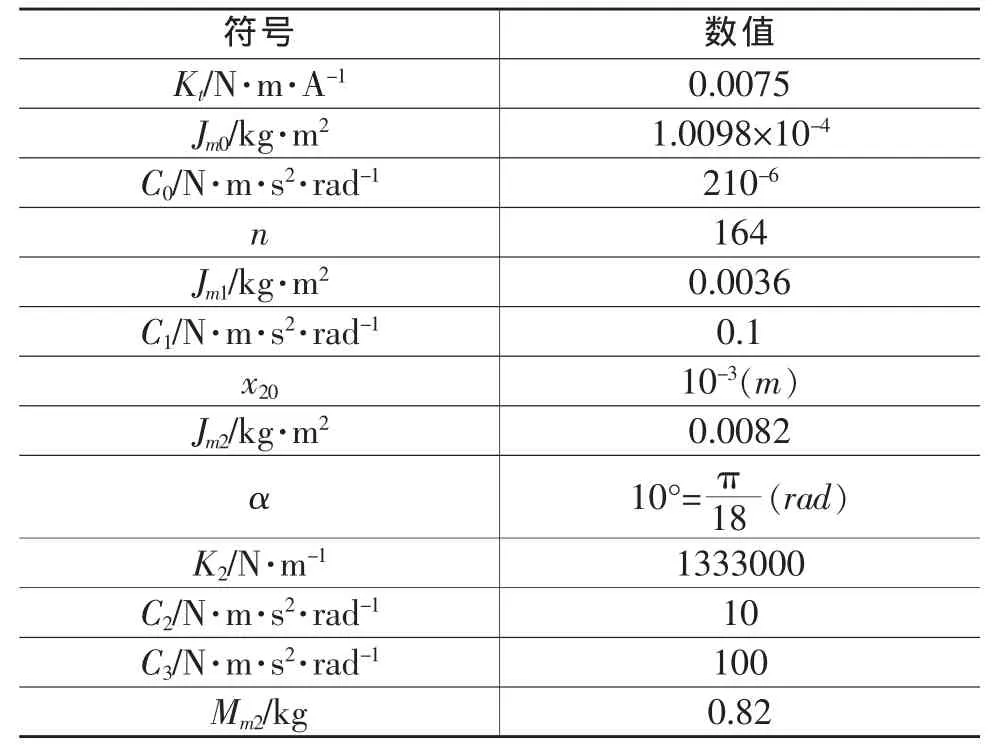
表1 物理参数
图2展示了试验中卡尔曼滤波器的两个输入结果曲线,卡尔曼滤波器的输出结果如图3所示。可见离合器正压力估计值对电流输入的响应十分迅速,但该响应滞后于力传感器的测量值约0.1 s,这一方面是因为在正压力值较小时压力传感器受干扰很大,对于本系统所采用的传感器,这一临界值大约为200 N;另一方面,本文中对实际系统进行了简化,在 X2<x20时,令F^n=0,而在 X2≥x20时,采用公式(39)给出正压力值的估计。
通过试验分析可见,卡尔曼滤波器能很好地反映离合器系统正压力随输入电流的变化情况,尤其是离合器压力从200 N开始增大到稳态的过程。
5 结束语
对直流无刷电机控制下的楔形离合器系统进行物理分析,忽略次要影响因素并使用卡尔曼滤波器原理建立了状态观测器。所建立的状态观测器能够很好地反映楔形机构对离合器组件发生推动作用时离合器系统的正压力值变化,表现出在多种输入电流下优秀且一致的跟踪特性。
实际系统当中,过程噪声的情况比本文更加复杂,本研究尚未通过对楔形离合器系统进行Monte Carlo仿真[10,11]来确定其过程噪声的协方差矩阵Q,后续研究中若能更加准确地描述系统的过程噪声,则可以使滤波器对正压力的估计更加贴近实际情况。
1 Luenberger,D.A.V.I.D."An introduction to observers."Automatic Control,IEEE Transactions on 16.6 (1971):596~602.
2 Alessandri,Angelo,and Paolo Coletta."Design of Luenberger observers for a class of hybrid linear systems."Hybrid systems: computation and control. Springer Berlin Heidelberg,2001.7~18.
3 R.E.Kalman.New Approach to Linear Filtering and Prediction Problems.Transactions of the ASME Journal of Basic Engineering,1960,pp.374~382.
4 Zarchan,Paul,and Howard Musoff.Fundamentals of Kalman filtering:a practical approach.Vol.208.Aiaa,2005.
5 Grewal,Mohinder S.,and Angus P.Andrews.Kalman filtering:theory and practice using MATLAB.Wiley.com,2011.
6 Barbot,J.,M.Djemai,and T.Boukhobza."Sliding mode observers."Sliding Mode Control in Engineering 11 (2002).7 Davila,Jorge,Leonid Fridman,and Arie Levant."Secondorder sliding-mode observer for mechanical systems."Automatic Control,IEEE Transactions on 50.11(2005):1785~1789.
8 Raisch,Jörg.Mehrgröβenregelung im Frequenzbereich.Vol.98.Oldenbourg Verlag,1994.
9 施颂椒,陈学中,杜秀华.现代控制理论基础.高等教育出版社,2009.
10 Jacoboni,Carlo,and Lino Reggiani."The Monte Carlo method for the solution of charge transport in semiconductors with applications to covalent materials."Reviews of Modern Physics 55.3(1983):645.
11 Burch,Richard,et al."A Monte Carlo approach for power estimation."Very Large Scale Integration (VLSI)Systems,IEEE Transactions on 1.1(1993):63~71.

