基于人工神经网络的波浪发电系统输出功率预测
霍政界
(河海大学能源与电气学院,江苏南京,211000)
0 引言
在能源渐趋枯竭、环境污染严重的当下,大力发展占地球表面积71%的海洋能已经成为时代的趋势。作为海洋中分布最广的可再生能源,波浪能具有良好的开发利用价值。但波浪发电也有其缺点,由于波浪的不规则性,不可控性等特点,波浪发电系统的输出功率也具有较大的波动性。这使得电力系统的运行调度难度增加。因此,若能对波电场的输出功率进行预测,就不仅对于其功率平滑控制有着重要的作用,同时也有利于电力系统消纳波浪发电系统的电能。
AWS 是第一个直驱式的波浪发电系统,2004 年在荷兰投入海底试运行,它的结构简单、效率高且完全淹没在水面下,所以易于被人们接受,本文以AWS 为例开展研究。
由于波浪数据的不规则性,本文选用能逼近任意非线性曲线的人工神经网络中的BP 算法,它具有很强的非线性映射能力,而且网络的中间层数、各层的处理单元数及网络的学习系数等参数都可根据具体情况设定,灵活性很大。本文用BP 算法对波浪数据建立网络模型,通过不同样本数据训练模型以及预测不同时间长度,得到不同预测结果,比对样本数据及预测时间长度对预测结果的影响。
1 基于AWS 的功率转化模型
1.1 阿基米德波能装置(AWS)
AWS 的底部固定于海底,上面由一个中空的气缸和一个浮子组成,浮子在波浪的起伏运动下往复运动,同时压缩气缸做功,将波浪能转化为机械能,从而带动直线永磁发电机发电。
1.2 简化的功率转化模型
文献[3]中根据牛顿第二定律给出了AWS 系统功率转换的详细模型。但其作为定义式,无法用于真是海面的计算。本文根据真实海面波浪周期不断变化的特点,对波浪力的计算采取了分段形式。
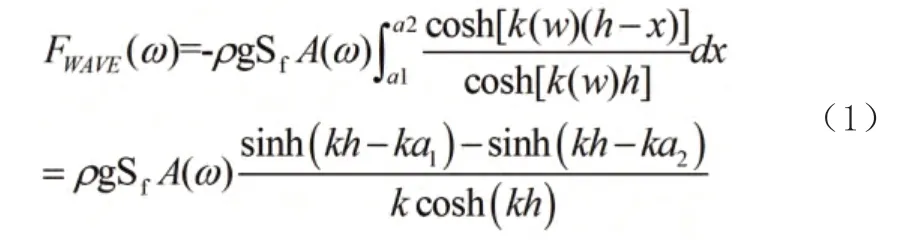
用于电力系统分析的AWS 驱动系统和直线永磁发电机可采用如下简化模型。
输出有功功率方程为:

式(1)、式(2)和式(3),构成了由波浪参数到功率的AWS 波浪完整转化模型,据此,搭建基于Matlab/Simulink 平台的仿真模型。
2 BP 神经网络基本原理
2.1 BP 网络介绍
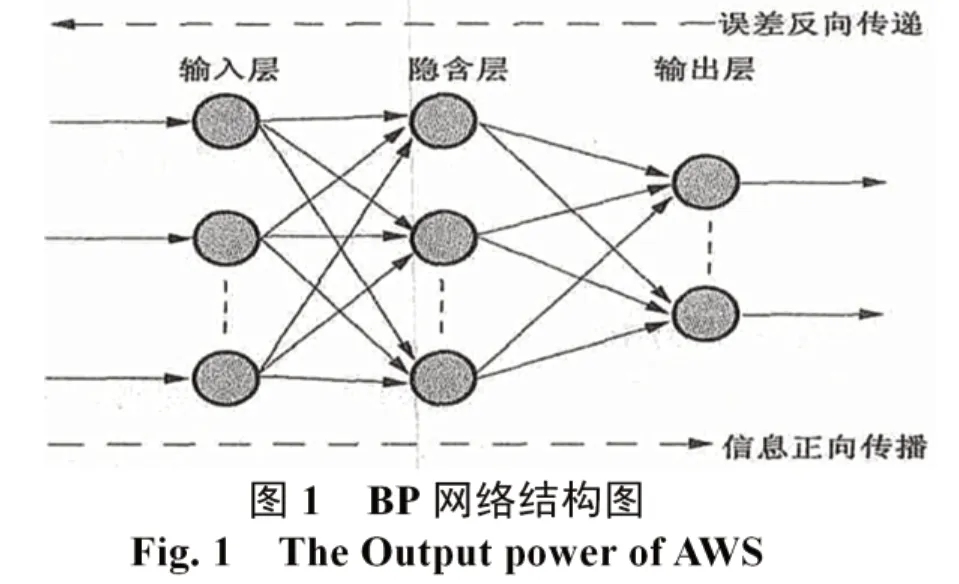
BP(Back Propagation)网络是一种按照误差反向传播的方法,最早由Rumelhart、McCelland 等人在1986 年提出。
BP 算法的学习规则是沿着表现函数下降最快的方向修正网络权值和阀值,使网络的误差平方和最小。BP 网络由输入层、隐含层和输出层构成。由于具有S 型函数的3 层BP 网络已经能够以任意精度逼近于任意连续函数,所以确定3 层结构BP 网络作为此次研究的基本模型(如图4)。网络的学习过程就是权值的调整过程,有两个过程组成,即:
1) 信号的正向传播
输入样本->输入层->各隐含层->输出层
2) 误差的反向传播
输出误差->隐层->输入层
2.2 基于BP 算法的预测模型
基于BP 算法的短期波浪数据预测模型可分为BP 神经网络构建、BP 神经网络训练和BP 神经网络预测三步。
a) BP 神经网络构建
BP 网络输入输出层的参数根据实际情况来决定。在隐含层节点数的选择上,根据以下公式而定:
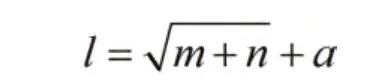
式中,l 为隐含层节点数; n 为输入节点数; m 为输出节点数; a 为1-10 直接的调节常数。改变l,用同一样本训练,从中确定网络误差最小时对应的隐含层节点数。
b) BP 神经网络训练
BP 神经网络的训练包括选取合适的传递函数、学习速率、期望误差等。传递函数是神经元间的传递方式,对网络的建模起着非常重要的作用。常见的传递函数有:线性函数(purelin)和sigmoid 型函数。
c) BP 神经网络预测
运用Matlab 软件进行预测,得到误差最小的预测值。
3 仿真分析
基于实测数据对波浪数据进行预测,测波点面向开敞黄海海区,无岛屿掩护,可观测到多个方向的波浪,波浪代表性良好。波浪站使用采样频率4Hz的SBF3-1型波浪浮标进行波浪数据采集,每1h 进行一次,采样间隔0.25s。为验证本文所提出的预测方法的有效性,这里选取了观测站2011 年8 月的一组波面数据中的3840 个连续点(4 点/s,共16min)用作样本数据。其中最后1min的数据用作预测目标值。
本文借助Matlab 工具箱中包含的各种函数开始分析样本数据。选取trainlm 函数为训练函数,将学习速率取为0.04,期望误差目标设为0.00033。
3.1 不同训练样本数量对的预测结果影响
分别取1440、1200、960、720、480 个训练样本来训练,滚动预测8 个点(即提前2s)预测,得到最后1min 的预测值与目标值得平均绝对误差mae 与平均绝对百分比误差map 如表1 所示:

表1 不同训练样本数量得到的预测误差
从预测结果可以看出,当训练样本数越多时,预测模型越准确,1200 个训练样本以上,误差值基本都很小了。所以,应选取合适的训练样本个数,使得训练的模型即精确又迅速。
3.2 不同预测时长对预测结果的影响
当取1200 个训练样本时,分别提前1s、2s、3s 进行预测,得到的误差值如表2 所示:
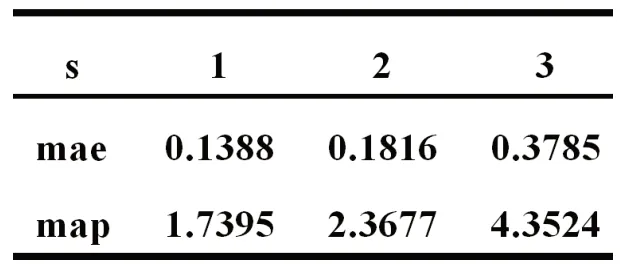
表2 不同预测时长得到的预测误差
从预测结果看,当预测超过3s 后,误差会变得很大,所以用这个模型进行预测的预测值最好在2s 以内。
3.3 功率预测值
将以1200 个点作为训练样本,提前2s 预测得到的预测值带入到功率转换方程,得到功率的预测值如下图所示:
4 结论
本文以AWS 波浪发电系统为例,建立了从波面数据到功率的简化模型,再利用BP 算法对实际波浪数据进行建模并预测,同时比对了不同训练样本数及预测时间长度对于结果的影响,最后选取合适的预测值带入功率转化模型中得到功率的预测值。可以看出,预测得到的输出功率比用正弦函数模拟得到的更为真实准确,并且能够充分反映现实中功率的变化,更有利于波浪发电系统的功率平滑控制。
但是,这样超短时间的预测对于波浪系统的并网运行帮助不大,后期应采取其它更为有效的预测方法来改进预测模型,以便得到更长时间的预测值。
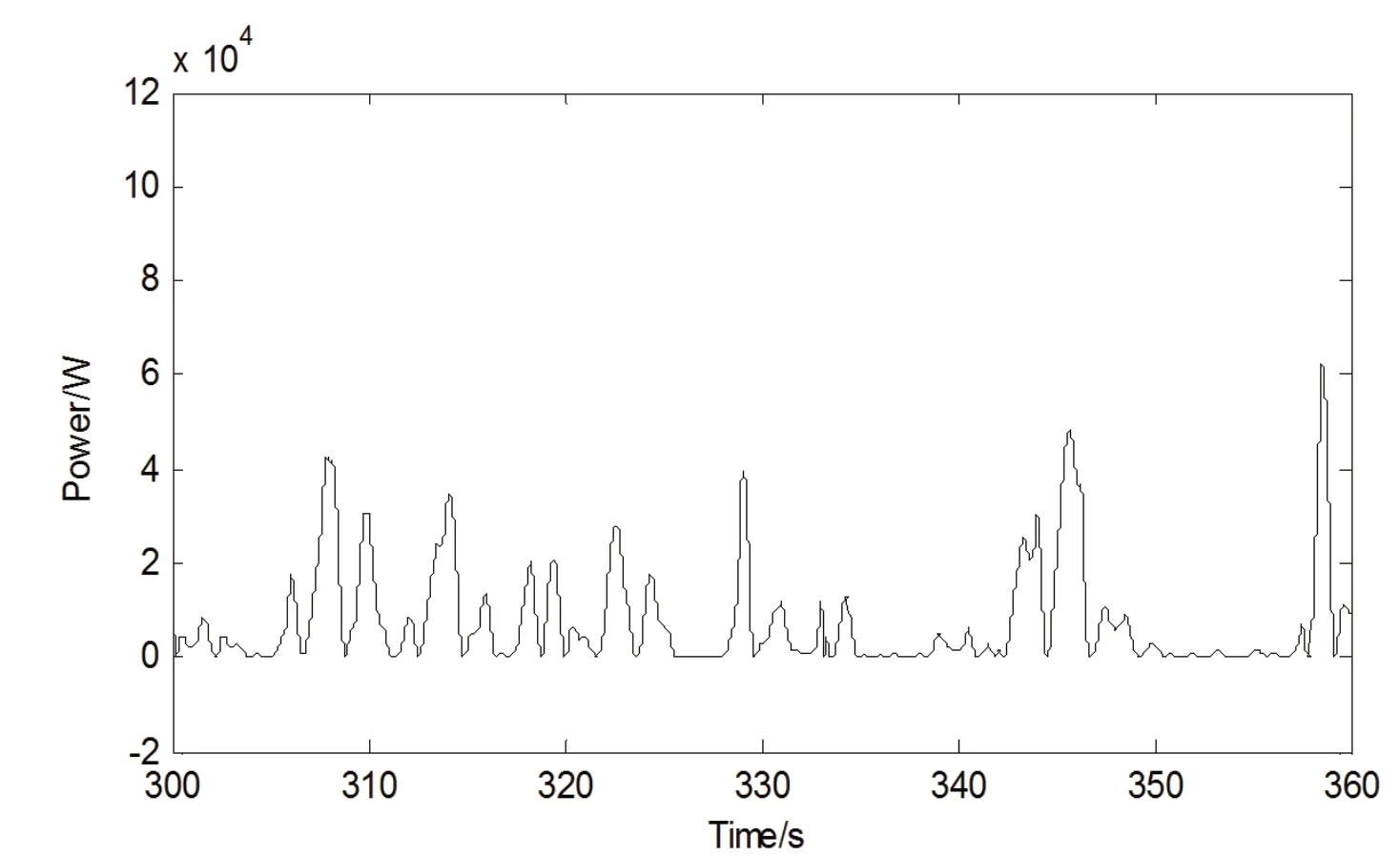
图2 输出功率Fig. 2 The Output power of wave
[1] 广州能源研究所.我国海洋波浪能的发展进展[EB/OL]. [2006-5-11].http://www.newenergy.org.cn/.
[2] De COSTA J S,PINTO P, SARMENTO A et al.Modeling of an Ocean Waves Power Device AWS[C]//Proceedings of IEEE Conference on Control Applications,2003: 618-623.
[3] Sousa Prado M G,Gardner F,Damen M,et al. Modelling and test results of the Archimedes wave swing[C]// Proceedings of the Institution of Mechanical Engineers,Dec,2006:855-868.
[4] WU Feng,ZHANG Xiaoping.Optimal Control for AWSBased Wave Energy Conversion System[J].IEEE Trans on Power Systems,2009,24(4):1747-1755.
[5] Simon Haykin.神经网络原理[M].叶世伟,史忠植译. 北京机械工业出版社, 2004:109-121 .
[6] 蒋宗礼.人工神经网络导论[M].北京高等教育出版社, 2001: 97-106.
[7] Martin Hagan T,Howard Demuth B,et al.神经网络设计[M].戴葵译.北京:机械工业出版社,2002:197-221.
[8] 张德丰.MATLAB 神经网络编程[M].化学工业出版社, 2011-12.

