基于EMD和Hilbert变换的脑磁信号特征提取和分类

王健锋， 黄晓霞

(上海海事大学 信息工程学院， 上海 201306)

0 引 言

脑机接口(Brain-Computer Interface，BCI)的目的是建立一种不依赖外周神经和肌肉组织的新型通信系统.该系统通过测量脑信号，如脑磁图(magnetoencephalography, MEG)，分析人类的意图，并将该意图转换为外部设备的控制信号.[1-2]因此，BCI可以给外周神经或肌肉组织受损的患者提供一种新的与外部世界交流的方式.BCI分为植入式BCI和非植入式BCI.非植入式BCI具有无创伤性、易于携带、价格低廉等优点，为BCI的实际应用和推广提供可能，成为BCI研究领域的一个热点.在非植入式BCI研究中，脑电图(electroencephalogram, EEG)和MEG是两种常用的输入信号.对EEG信号的研究已经取得很大成就，但是EEG信号的采集容易受到头盖骨的影响，导致其空间分辨率不高，误差很大，使EEG的应用范围受到限制.MEG不受头盖骨的干扰，具有较高的时空分辨率和更低的失真率，能够直接反映脑内场源的活动状态，受到不少BCI研究者的青睐.[3-4]

在2008年第4届国际BCI竞赛中，第3组数据使用的就是MEG数据，许多研究机构参加这次竞赛，其中HAJIPOUR等获得该组竞赛的第一名，他们用统计特征、自回归模型和小波变换的方法进行特征提取，用有监督的遗传算法进行特征降维，用线性判别分析(Linear Discrimination Analysis, LDA)和支持向量机(Support Vector Machine, SVM)进行分类，所得MEG的平均分类准确率为46.9%.我国燕山大学的李静等获得第二名，他们用快速傅里叶变换和主成分分析(Principal Component Analysis, PCA)法进行特征提取，用Fisher线性判别(Fisher Linear Discrimination, FLD)方法进行特征降维，用LDA进行分类，所得MEG的平均分类准确率为25.1%.2011年SABRA等[5]对该MEG进行研究，用统计特征、功率谱密度和离散小波变的方法进行特征提取，分别用LDA和SVM进行分类，获得33.3%的平均分类准确率.虽然这些特征处理方法能够获得不错的结果，但都没有兼顾分类准确率和处理方法简易性，即分类准确率高时，处理方法比较复杂，处理方法简单时，分类准确率却不高.

在不明显降低分类准确率的情况下，兼顾MEG识别率和处理方法的简易性，本文提出一种基于经验模式分解(Empirical Mode Decomposition, EMD)和Hilbert变换的MEG特征提取和分类方法.这是一种时频数据的处理方法，非常适用于非线性和非稳定性信号的处理，在轴承故障诊断、肌电信号分析和基于EEG的BCI研究方面都能取得不错的效果，但目前该方法还没有被应用到基于MEG的BCI研究中.为验证EMD和Hilbert变换对基于MEG的BCI的处理性能，使用EMD和Hilbert变换对MEG进行特征提取，然后用PCA法对提取到的特征向量进行特征降维，最后用SVM进行分类.

1 数据描述

本文选用第4届国际BCI竞赛的第3组数据.该数据记录两名健康的右利手实验者S1和S2在执行手腕运动期间的脑部活动信息.采集数据时，两名实验者坐在带有MEG采集设备的椅子上，保持放松，把肘部放在枕垫上以防止上臂和肩运动，头部用小枕头固定.要求实验者仅仅使用右利手和手腕从中心位置向与其夹角为90°的4个方向移动一个操纵杆，运动幅度是4.5 cm.在每次实验中，方向由实验者自己选择，目标位置在菱形的4个角上，分别表明左、右、远离实验者、朝向实验者.

该MEG数据记录头部运动区域上的10个信道(LC21，LC22，LC23，LC31，LC32，LC41，LC42，RC41，ZC01和ZC02)的信号(包含运动开始前0.4 s至开始后0.6 s的数据)，并通过频带0.5～100 Hz的带通滤波器以采样率400 Hz进行重新采样.本实验所使用的MEG数据包括：实验者S1的160次训练数据(每个目标方向分别进行40次实验)和74次测试数据；实验者S2的160次训练数据(每个目标方向分别进行40次实验)和73次测试数据.

2 方法描述

2.1 基于EMD和Hilbert变换的特征提取

2.1.1 EMD

EMD主要思想是从复杂信号里分离出有限个本征模函数(Intrinsic Mode Function，IMF)，这些IMF具有不同的频率，并且满足：①其极值点个数与过零点个数相同或相差一个；②其上下包络关于时间轴局部对称.[6-8]EMD具体分解过程如下.

(1)对任一信号x(t)，首先确定x(t)上所有的极大值点和极小值点，然后用三次样条函数将所有极大值点拟合成原数据序列的上包络线，将所有极小值点拟合成原数据序列的下包络线.

(2)计算上下包络线的均值曲线m1(t)，将原数据序列x(t)减去m1(t)可得到一个新的数据序列h1(t)，即

(1)

(3)判断h1(t)是否满足IMF定义.若满足，信号x(t)第1个IMFc1(t)=h1(t)；若不满足，将h1(t)作为原信号，重复上述步骤，执行k次，直到h1k(t)满足IMF的定义为止，即得信号x(t)第1个IMFc1(t)=h1k(t).

(4)将第1个IMFc1(t)从x(t)中分离出来，得到一个去掉高频分量的剩余信号r1(t)，即

(2)

(5)将r1(t)作为原信号，重复上述步骤，可得到其他IMF，直到剩余信号是一个单调函数或只有一个极值时筛选过程结束.最终原始信号x(t)可表示为

(3)

式中：ci(t)代表每个IMF；rn(t)代表剩余信号.

2.1.2 Hilbert变换

经过EMD后，对每个IMF进行Hilbert变换，可得到原始信号的Hilbert谱.[9-10]具体步骤如下.

对每个IMF作Hilbert变换得

(4)

(5)

这里省略剩余信号rn(t)，Re表示取实部，其中每个IMF的幅值和相位随时间改变.式(5)等号右部称为信号x(t)的Hilbert振幅谱，简称Hilbert谱，记为

(6)

该公式将信号的时间-频率-幅值的三维关系表达出来，其含义是瞬时振幅在频率-时间上的分布.

对Hilbert谱取平方可得Hilbert能量谱H2(w,t).在此基础上，定义瞬时能量密度

(7)

很显然,瞬时能量密度EI是一个关于时间的函数，反映能量在时间上的波动.

2.2 基于PCA法的特征降维

PCA法是揭示大样本、多变量数据或样本间内在关系的一种方法，旨在利用降维的思想，把多指标转化为少数几个综合指标，降低观测空间的维数，以获取最主要的信息.通常把转化生成的综合指标称为主成分，每个主成分都是原始特征的线性组合，并且各个主成分之间互不相关，这就使得主成分比原始特征具有某些更好的性能.[11-12]

在实际的降维过程中，根据前m个主成分的累积方差贡献率决定特征向量的维数.当前m个主成分的累积方差贡献率大于给定的上限值时，可取前m个主成分作为特征向量，达到降维目的.

2.3 基于SVM的分类

SVM是一种基于统计学习理论的机器学习方法，它首先选择某种非线性映射算法将输入向量映射到一个高维特征空间，在该高维特征空间中利用结构风险最小化原则和间隔的概念，构造最优线性决策函数，求解最优分类超平面，达到分类的目的.[13-14]

3 实验过程

本文所提出的算法包括预处理、特征提取、特征降维和分类等4个步骤，其实验流程见图1.

图1 算法实验流程

3.1 预处理过程

本实验所采用的MEG数据在频带0.5～7 Hz范围内包含的运动方向信息最为明显[15]，故将这10个信道的MEG数据通过频带为7 Hz的低通滤波器进行滤波处理.

3.2 特征提取过程

使用EMD对预处理后的MEG数据进行分解，得到各信道中各样本的IMF.其中某信道单个样本经EMD后得到的结果见图2.从该图可以看出，经EMD所得的剩余信号逐渐趋于平滑，故弃之不用，只选取经EMD得到的IMF.

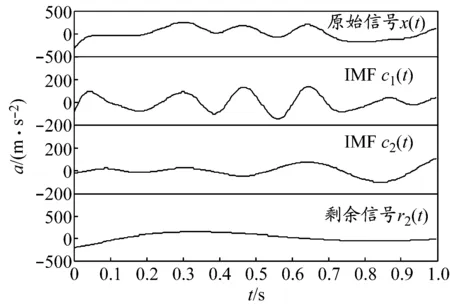
图2 某信道单个样本经EMD后的结果

用基于Hilbert变换的方法计算每个样本的IMF的瞬时能量密度，并将其组合为MEG的特征向量，用于区分MEG的运动方向.将图2所对应样本的IMF进行Hilbert变换后，计算其瞬时能量谱，能量随时间的变化情况见图3.

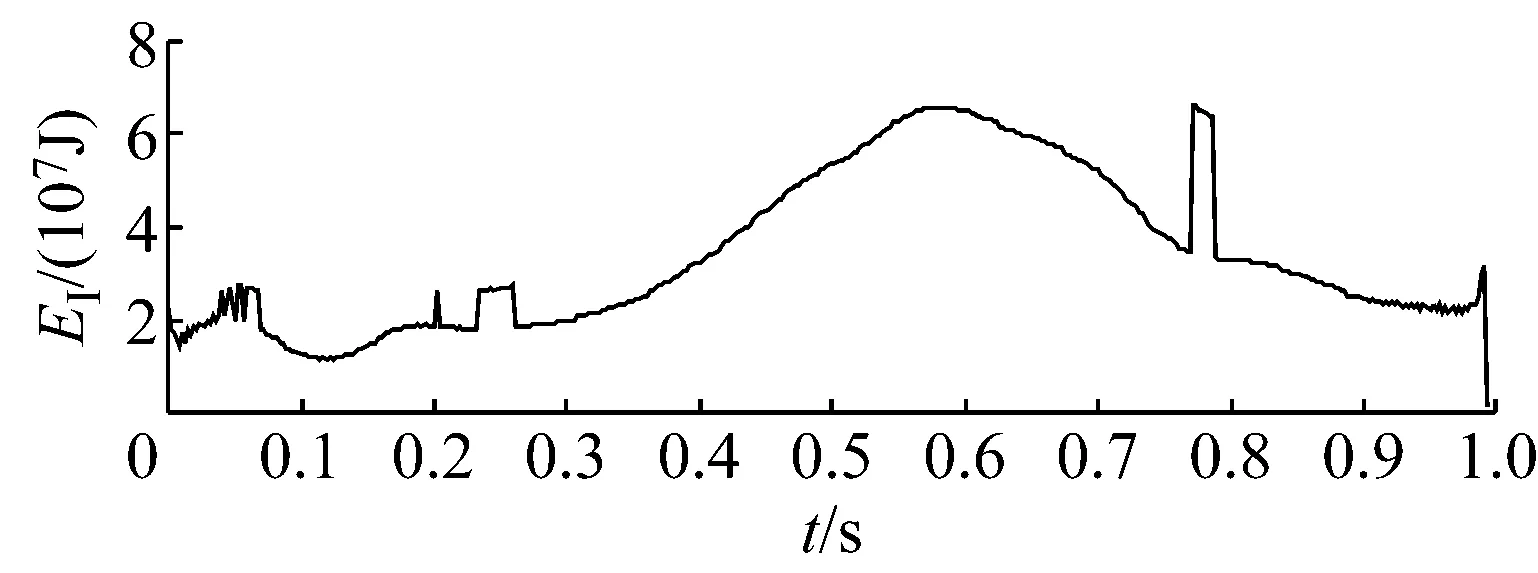
图3 样本IMF的瞬时能量谱

3.3 特征降维过程

提取MEG数据的特征后，得到单个MEG样本单个通道的瞬时能量谱为398维，每个样本共有10个通道，若将单个样本的10个通道的瞬时能量谱组合为该样本的特征向量，特征向量的维度将高达3 980.为避免复杂的计算且提高分类准确率，在分类之前对特征向量进行特征降维.在本实验中，使用PCA法将特征向量的维度降为159，然后根据主成分的累积方差贡献率的原则取其前26个主成分，并将归一化处理过的26个主成分作为MEG的特征向量.

3.4 分类过程

本实验使用基于线性核函数的SVM对获得的特征向量进行分类.为获得较好的分类效果，对SVM的惩罚因子C进行寻优.图4是S1和S2的分类准确率随C的变化情况.从图4可知，当C达到22时，S1和S2的平均分类准确率达到最高值，为44.3%。

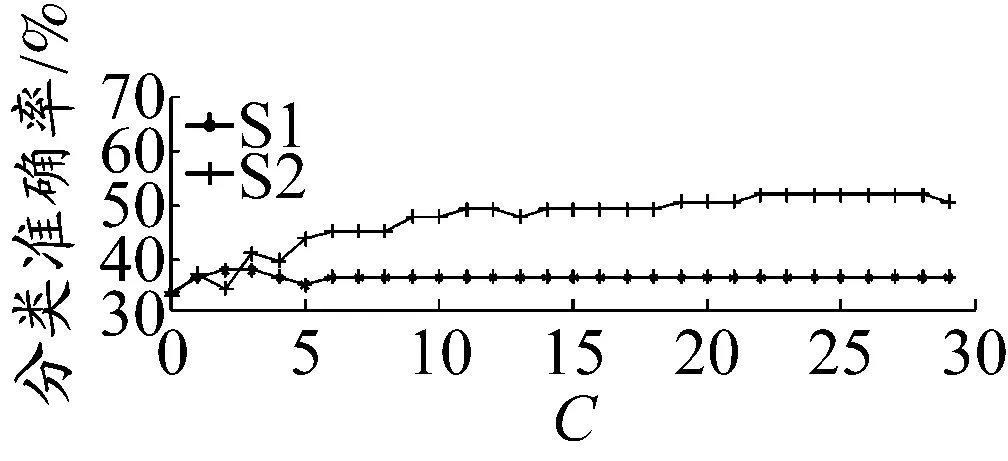
图4 S1和S2分类准确率随C的变化

3.5 实验结果分析

通过本文提出的算法获得的分类结果：S1和S2的分类准确率以及二者的平均分类准确率分别为36.5%，52.1%和44.3%.而第4届国际BCI竞赛各个竞赛小组所获得的分类结果见表1.其中竞赛第一名分别提取MEG的时域特征、频域特征和时频特征作为的联合特征，竞赛第二名分别提取MEG信号的时域特征和频域特征作为信号的联合特征.

表1 第4届国际BCI竞赛结果 %

采用本实验所使用的算法获得的测试集的平均分类准确率比竞赛第二名所获得的平均分类准确率高19.2%，虽没能超过竞赛第一名所获得的分类准确率，但只与竞赛第一名所获得的平均分类准确率相差2.6个百分点.本实验特征提取算法使用的是EMD和Hilbert变换，只需提取信号的时频特征，比竞赛第一名所使用的特征提取算法简单且易于实现；本实验使用PCA法进行特征降维，与竞赛第一名所使用的遗传算法相比，时间复杂度降低很多；本实验分类器只选用线性SVM，使算法复杂度和时间消耗降低.本算法在奔腾处理器、主频2.1 GHz和1 G内存的Window XP下处理整个MEG数据的运行时间是281 s，而竞赛第一名所使用的算法在奔腾处理器、主频3 GHz和1 G内存的Windows XP下的运行时间是1 043 s，在运行环境基本相同且计算机性能并不占优势的情况下，本算法的运行时间显著减少.总体来说，在MEG分类准确率不明显降低的情况下，本算法的实现比较简单，且时间性能优于竞赛第一名所使用的MEG数据处理算法.

4 结束语

实验结果表明，本文提出的基于EMD和Hilbert变换的特征提取和分类算法不仅能够用于MEG数据的分类，而且能够获得较高的分类准确率和较优的时间性能，综合性能较好，具有更高的实际应用价值.由于本研究还在进行中，该算法还有许多地方可以改进，下一步的目标是进一步提高该算法的分类准确率.

参考文献：

[1] SARDOUIE S H, SHAMSOLLAHI M B. Selection of efficient features for discrimination of hand movements from MEG using a BCI competition IV data set[J]. Frontiersin Neuroscience, 2012(6): 42-47.

[2] 高上凯. 基于节律性脑电信号的脑-机接口[J]. 生命科学, 2008, 20(5): 722-724.

[3] 吴婷, 颜国正, 杨帮华. 基于小波包分解的脑电信号特征提取[J]. 仪器仪表学报, 2008, 28(12): 2230-2234.

[4] KRISHNA S, VINAY K C, RAJA K B. Efficient MEG signal decoding of direction in wrist movement using curve fitting (EMDC)[C]// 2011 Int Conf Image Inform Proc (ICIIP). IEEE, 2011: 1-6.

[5] SABRA N I, WAHED M A. The use of MEG-based brain computer interface for classification of wrist movements in four different directions[C]// 2011 28th Natl Radio Sci Conf (NRSC). IEEE, 2011: 1-7.

[6] LEI Y, LIN J, HE Z,etal. A review on empirical mode decomposition in fault diagnosis of rotating machinery[J]. Mech Systems & Signal Processing, 2013, 35(1): 108-126.

[7] LI Lin, JI Hongbing. Signal feature extraction based on an improved EMD method[J]. Measurement, 2009, 42(5): 796-803.

[8] MENDEZ O, CORTHOUT J, Van HUFFEL S,etal. Automatic screening of obstructive sleep apnea from the ECG based on empirical mode decomposition and wavelet analysis[J]. Physiol Measurement, 2010, 31(3): 273-289.

[9] HUANG N E, WU M L, QU W,etal. Applications of Hilbert-Huang transform to non-stationary financial time series analysis[J]. Appl Stochastic Models in Business & Industry, 2003, 19(3): 245-268.

[10] PANOULAS K I, HADJILEONTIADIS L J, PANAS S M. Hilbert-Huang spectrum as a new field for the identification of EEG event related de-synchronization for BCI applications[C]// 30th Annu Int Conf Eng Med & Biol Soc (EMBS). IEEE, 2008: 3832-3835.

[11] 张颖. 基于PCA的模糊BP网络建模方法在藻类生长状态预测中的应用[J]. 上海海事大学学报, 2011, 32(4): 76-79.

[12] JOHNSTONE I M, LU A Y. On consistency and sparsity for principal components analysis in high dimensions[J]. J Am Stat Assoc, 2009, 104(486): 682-693.

[13] 安博文, 李丹, 庞然. 基于 SVM 分类器的集装箱箱号识别法[J]. 上海海事大学学报, 2011, 32(1): 25-29.

[14] 冯超, 贺俊吉, 史立. 基于支持向量机的轿车车型识别[J]. 上海海事大学学报, 2011, 32(3): 85-89.

[15] WALDERT S, PREISSL H, DEMANDT E,etal. Hand movement direction decoded from MEG and EEG[J]. J Neuroscience, 2008, 28(4): 1000-1008.