考虑物流服务水平影响的三级物流服务供应链协调
何婵, 刘伟, 崔爱平
(1. 上海海事大学 交通运输学院,上海 201306; 2. 江西财经大学 统计学院, 南昌 330013)
0 引 言
物流服务供应链(Logistics Service Supply Chain,LSSC)以“物流服务分包商←物流服务集成商←物流服务需求方”为基本结构[1],其中物流服务集成商是整个供应链的核心企业,它从物流服务分包商处订购物流能力满足最终物流需求客户的要求.国内外关于服务供应链的研究[2-6]较多,其中LSSC是一种典型的服务供应链,有其独特的行业性质.LSSC的研究近些年才引起学者重视,而协调问题是其中一个重要的研究内容.LSSC协调是LSSC成功运作和绩效提升的关键性问题,对提高物流企业的竞争优势具有非常重要的实践意义.LSSC协调主要通过对物流能力的调整和优化实现.由于物流能力具有无形性、生产与消费同步、无法存储的特征,LSSC在协调时不同于一般商品供应链.田宇等[7]从一般产品供应链的思路出发,建立二阶段和三阶段LSSC收益分享契约模型.刘伟华等[8]研究LSSC两级能力合作的协调,分别构建不确定环境下有/无能力匹配约束时的物流服务集成商成本模型和提供商的利润模型.崔爱平等[9]提出LSSC中基于期权契约的能力协调,指出期权契约价格与期权执行价格之间存在负相关关系.桂云苗等[10]考虑供应能力不确定的LSSC协调.王晓立等[11]研究供应和需求不确定条件下的LSSC协调.LIU等[12]基于两阶段单周期质量协调模型建立一个多周期LSSC质量协调模型.
以上研究的都是二级LSSC.实际LSSC通常由3个或更多实体组成.三级LSSC是二级LSSC的扩展,由3个实体构成,存在2个交易过程,比二级LSSC复杂得多.如何协调这三者之间的关系,使供应链整体最优,是协调机制设计的主要困难.通常二级LSSC的协调方法在三级LSSC中不一定适用.对三级LSSC协调的研究目前还不多.公彦德等[13]基于传统二级供应链协调问题,引入第三方物流服务提供商,应用博弈理论对三级供应链的定价、产量和利润进行分析,发现零售商所承担的服务价格比例越大,各节点企业的利润也越大,因而通过设置合理的分摊比例,可以达到优化供应链的目的.刘伟华[14]用收益共享契约协调三级LSSC,并给出最优收益共享系数的确定方法.朱卫平等[15]研究三级LSSC协调,提出一种数量协作联盟的协调模型.以上文献虽然从不同的角度采用不同的契约研究三级LSSC协调问题,但没有考虑物流服务水平对需求的影响,且仅仅用一种契约实现三个节点企业之间的合作,而在现实中,企业为追求更好的利润,与不同的合作实体可能签订不同的契约.研究表明,在特定条件下一些经过精心设计的组合合同策略能促成供应链的协调,使供应链整体利润达到最大化.[16-17]而目前鲜有文献研究不同契约组合能否协调的问题,本文就此开展研究.
另一方面,物流服务水平的高低对顾客是否有再次购买行为有直接、显著的影响.[18]LU等[19]研究制造商的服务水平对零售商价格的影响,指出制造商存在一个最优的服务水平.吴庆等[20]研究物流服务水平影响市场需求的第三方物流协调合同,设计一种收入共享与服务成本共担的组合式合同,该合同既可以协调第三方物流服务提供商的物流服务水平决策,又能协调客户企业的存货决策,并且能实现共赢.XIAO等[21]针对一个供应商和一个零售商组成的供应链,研究根据供应商管理库存协调价格和服务水平的问题.但以上文献主要是针对产品供应链协调.
在现实生活中,当物流服务分包商提供的服务水平达到或超过顾客期望时,顾客的满意度得到提高,对产品的市场需求会增加,从而会使物流服务需求方对集成商的物流需求增加.与产品供应链不同,LSSC的收入来源于物流服务需求方,在其他条件不变的情况下,提高物流服务水平并不能给LSSC带来更多直接的收益,但会带来更好的信誉和更多的物流服务需求[22-23],从而间接增加LSSC收益.因此,在LSSC中,集成商决策物流能力订购量,提供商决策给集成商的分包价格,物流服务分包商除了决策给提供商的分包价格外,还要决策物流服务水平,因为努力需要成本,如果没有足够的激励,分包商会倾向于偷懒.在这种情形下,如何设计合理的契约机制激励分包商努力提高服务水平从而实现系统协调是一个值得研究的课题.
综上所述,本文研究由“物流服务分包商←物流服务提供商←物流服务集成商”组成的三级LSSC,从激励分包商提高物流服务水平角度,设计一种集成商与提供商之间实行期权契约、提供商与分包商之间实行成本共担收益共享契约的联合契约协调机制,建立基于能力协调的三级LSSC定量模型,实现LSSC系统利润最大,保证各成员获得共赢.最后通过算例分析验证契约的可行性和有效性.
1 问题描述
考虑一个由物流服务集成商(R)、物流服务提供商(F)、物流服务分包商(S)组成的三级LSSC,其中R在供应链中起主导作用,它从F处订购物流能力满足最终物流需求客户的要求.而F由于自身能力不足,将部分或全部物流能力外包给其上游的S,为简化起见,假设F将订单全部转包给S,S完全能够满足F的物流需求.客户需求x是随机的,服从随机分布函数F(x),其密度函数为f(x),均值为μ,方差为σ2.因为需求不确定,R希望得到的物流能力足够满足市场需求以应对风险和实现自身利益最大化,但S的物流能力投资可能会有风险与机会成本损失.假设:(1)供应链成员均是有限理性和风险中性,他们之间均信息对称,且根据期望利润最大化的原则进行决策;(2)S的初始物流能力为零,面对随机的物流服务需求,S不存在能力短缺损失情形;(3)物流服务水平的高低可以度量,也可以被证实.高水平的物流服务质量可以使顾客对客户企业的产品产生更大的市场需求.[12]这里假设在考虑物流服务水平e的影响下,新的市场需求x′=ex.

分别用S(Q,e),L(Q,e)和I(Q,e)表示R的物流能力期望值、缺货期望值和富余能力期望值.
S(Q,e)=E(min(Q,ex))=
(1)
L(Q,e)=E(max(ex-Q,0))=
(2)
I(Q,e)=E(max(Q-ex,0))=
(3)
命题1S(Q,e)(e≥1)关于e单调递增.
命题1说明提高物流服务水平可增加期望物流能力订购量.
2 集中决策系统
集中决策系统见图1.
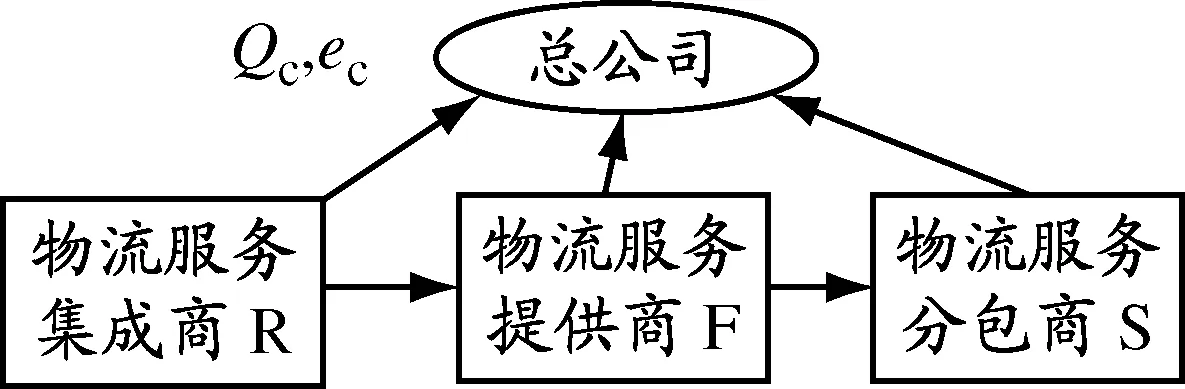
图1 集中决策系统
将R,F,S看作同属一家公司(见图1),其目标是确定最优的Qc和ec使整个LSSC利润最大.这一结果虽然在现实中往往因各成员追求各自利益最大化而难以实现,但依然有助于分析本文设计的契约能够在多大程度上协调LSSC.系统的收益模型为
(4)
其中:c=cR+cF+cS.
(5)
化简得
(6)
同时确定ec,
即ec满足
(7)
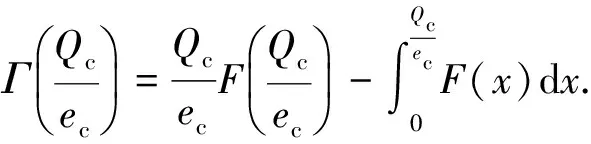
由式(6)可知,LSSC的订购量与S的服务水平成正比,即通过提高物流服务水平,可使LSSC的订购量增加.进一步可求得LSSC最大总收益的期望值为
(8)
由式(8)可知,物流服务水平越高,系统收益越大.
命题2πT(Qc,ec)≥πT(Qc,ec=1)
命题2表示在集中决策系统中,提高物流服务水平会使系统获得更高的收益,这说明在讨论LSSC协调时,考虑物流服务水平是必要的.
3 Stackelberg博弈模型
Stackelberg博弈模型见图2.
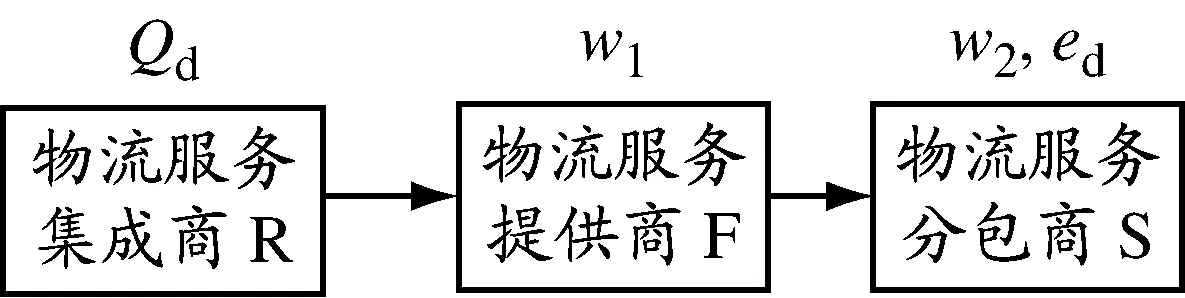
图2 Stackelberg博弈模型
LSSC运作的本质是相互独立的成员构成分散式系统,各成员都按照自身利益最大化进行决策.在Stackelberg博弈下,首先R给出订购量Qd, F根据Qd给出w1,S在已知Qd和w1的基础上决策w2和ed,F反过来再修正w1,最后R修正Qd.R,F,S的收益函数分别为
πR(Qd)=pS(Qd,ed)-(cR+w1)Qd-
gL(Qd,ed)+vI(Qd,ed)
(9)
πF(w1)=w1Qd-cFQd-w2Qd-
vI(Qd,ed)+HI(Qd,ed)
(10)
πS(w2,ed)=w2Qd-cSQd-HI(Qd,ed)-
(11)
因为
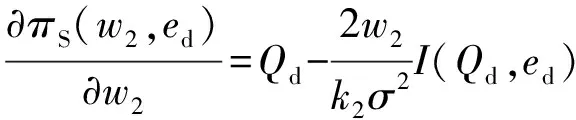
所以存在唯一最优的w2为
(12)
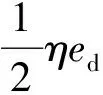
即ed满足
(13)
在给定ed的情况下,F要实现利润最大化,w1须满足
(14)
已知ed,w1,w2,R要实现自身收益最大化,决策变量Qd必须满足一阶条件:
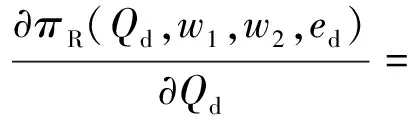
(15)
将式(13)和(14)代入式(15)就能得到Qd的最终形式.
4 联合契约协调及最佳决策
协调机制设计:首先假设R与F合作,可以把他们看成一个整体RF,他们之间先采用期权契约进行协调;其次S与RF采用成本共担收益共享契约进行协调.这样的设计首先可以分担S的努力成本,激励S物流能力投入,同时可以减小R和F的风险,提高系统收益.本文分析和证明通过合理的契约参数设计,可实现三级LSSC的整体协调.决策过程见图3.
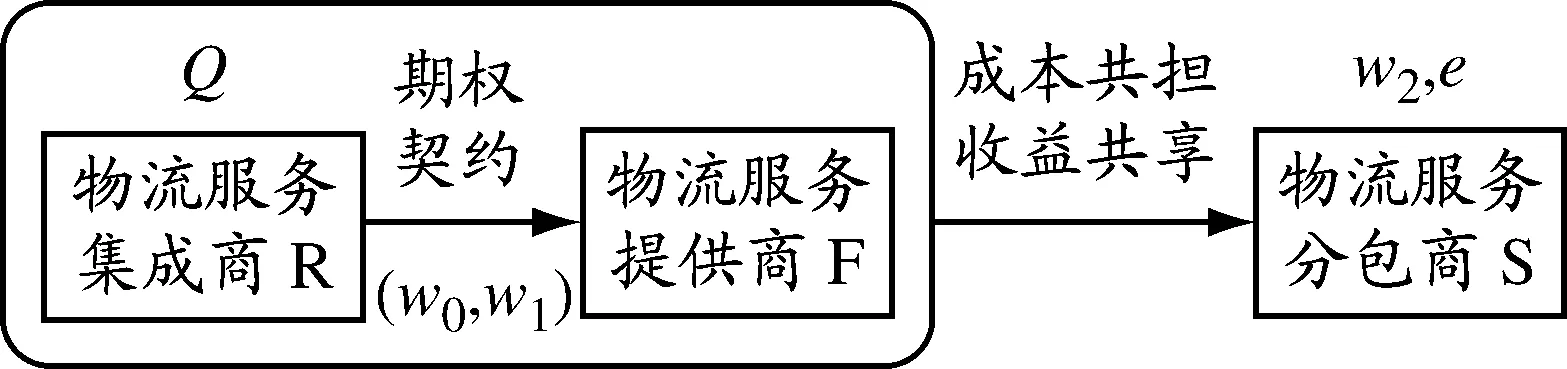
图3 联合契约协调示意
4.1 R与F之间的期权契约
期权为R以较低风险从F处获得产品的柔性机制,R和F可以在一定程度上共享市场需求信息,用于分担R的风险、提高决策精度、增加整体收益.R在LSSC中处于主导地位,因此,与F的期权契约的决策顺序如下:
(1)期初,R与F谈判,提出期权契约(w0,we).
(2)F根据期权契约给出w1.
(3)R根据(1)和(2)的信息决定初始订购量Q0和期权购买量q0.
(4)F接受期权契约,准备物流能力.
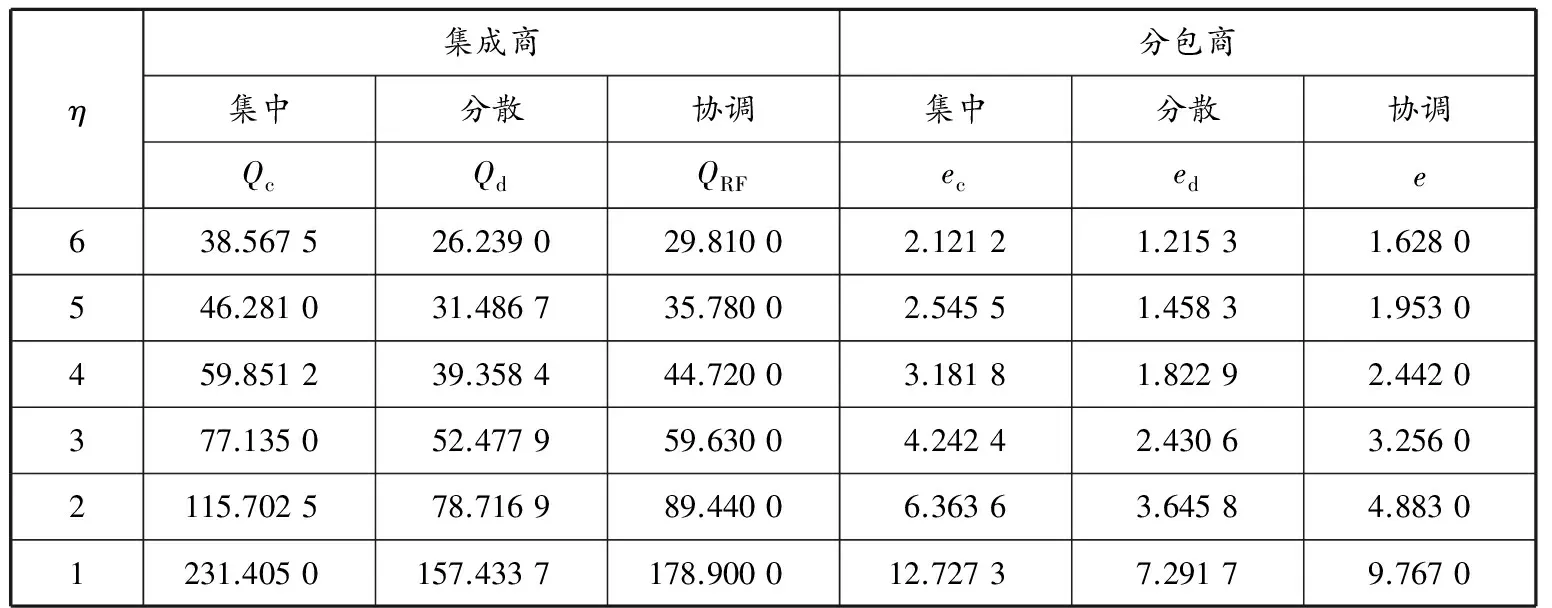
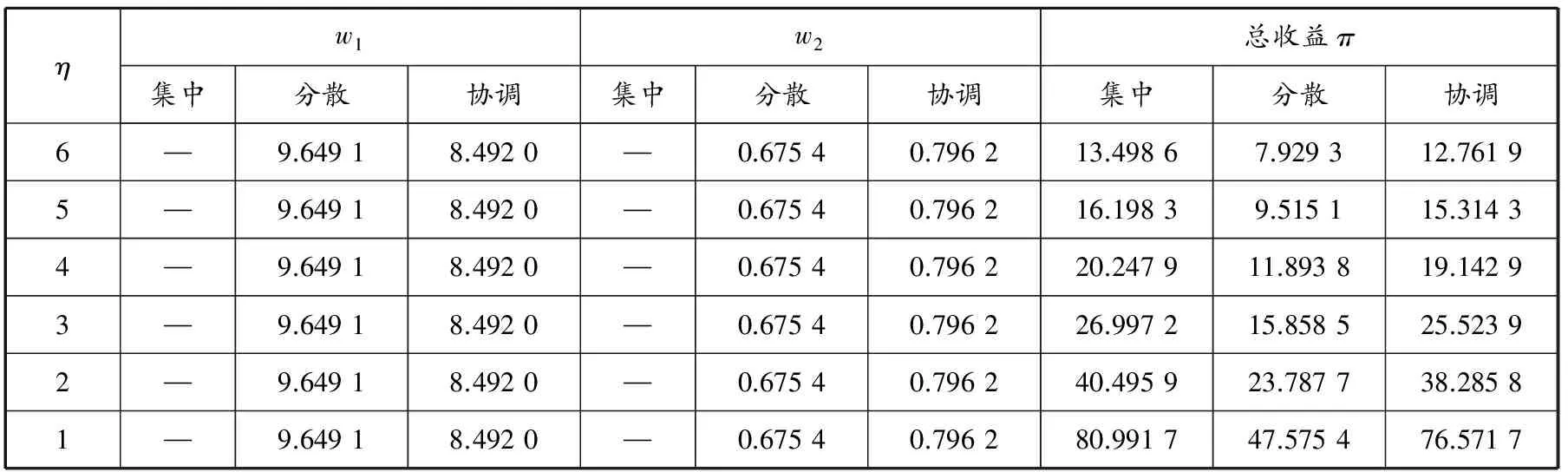
(5)期末,R以单价p提供集成化的物流服务给物流服务需求企业,并根据已经签订的订单获得下一周期的实际需求情况.当实际需求x>Q0时,R将以we的价格执行期权购买量qe.这种情况下F物流能力的实际交付量为Q0+qe,其中qe=min{max{x-Q0,0},q0},即
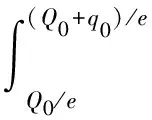
当Q0>x时,说明实际订购量大于市场需求量,此时qe=0,R实际上不执行期权,多余的物流能力退还给F时可得到vmax{Q0-x,0}的成本返回额.当Q0+qe R的期望收益为 πR(Q0,q0,w0,we)=pS(Q0+q0,e)+vI(Q0,e)-w1Q0-w0q0-weE(q)-cR(Q0+E(q))-gL(Q0+q0,e)= (16) 在期权契约下,F可以获得的期望收益为 πF(w1)=w1Q0+w0q0+weE(q)-cF(Q0+E(qe))-vI(Q0,e)+HI(Q0,e) (17) 通过期权契约,LSSC能增加F的备货量,减小R的风险,但同时F也可能会因此遭受备货量过大的成本风险.期权契约虽然能给成本风险带来一些补偿,但F作为理性的经济人,当然希望收益更大而损失更小.因此,F与上游S之间采用成本共担收益共享契约是一个合理的选择.由于F的备货量受R订货量的影响,从而最终受市场需求的影响,可以把R和F合看作三级LSSC的一个子系统RF,设RF将1-K份收益分给S,并与S分担1-θ份努力成本,其中K,θ∈[0,1],那么,RF的共同收益为 (18) 此时,S的期望收益为 (19) 定理1在期权契约与成本共担收益共享契约组成的联合契约下,如果要实现供应链系统的完全协调,则K,θ∈A,且契约参数必须满足 定理2R的最佳物流能力订购决策(Q0,q)为:(a)当(p+g-cR)w0-(p+g-we-cR)w1<(p+g-w0-we-cR)(cR-v)时,R的最佳订购量和期权购买量如式(20)和(21)所示;(b)当(p+g-cR)w0-(p+g-we-cR)w1≥(p+g-w0-we-cR)(cR-v)时,R的最佳订购量与分散式的最佳订购量一致,即Q0=Qd,q0=0. 上述契约一般由LSSC成员通过谈判协商确定初始参数.只有合理设计参数,才能使契约实现对供应链系统的整体协调.在合理的范围内,契约参数的大小与企业的讨价还价能力有关. 下面结合算例分析本文的联合协调契约.假设x服从均匀分布U(0,B). 基于以上假设由式(6)~(8)可得集中决策供应链的最优解. (20) (21) 根据式(12)~(15)可得到Stackelberg博弈模型的最优解. (22) (23) (24) (25) 则整个供应链系统的最优解为 (26) 由式(19)和假设(1)可得 (27) 2θηBe3+2B(1-K)gμe2= (28) 从LSSC实际运作中提炼出的参数见表1.由式(20)~(28)求得三级LSSC的最优决策、最优价格决策和总收益,分别见表2和3. 分析以上结果可知:(1)联合协调能够协调LSSC,实现系统帕累托改进.联合协调系统的总收益比较接近集中决策系统的总收益,比Stackelberg博弈系统收益高.联合协调和集中决策情况下R的订购量和S的努力水平较Stackelberg博弈情况下都有所上升.(2)从物流能力定价上看,在联合协调情况下,F提供给R的物流能力价格较分散情况下有所降低;S提供给F的物流能力价格较分散情况下整体上升.S的服务成本系数对物流能力定价无显著影响.(3)R的物流能力订购量随着S的物流服务成本系数的增加而减少.(4)物流服务成本系数越大,S愿意付出的努力越小.(5)S努力情况下系统的收益比S不努力情况下的高. 表1 三级LSSC的相关参数 表2 三级LSSC的最优决策 表3 三级LSSC的最优价格决策和总收益 本文研究由物流服务集成商、提供商和分包商组成的三级LSSC协调模型,在考虑物流服务水平影响需求变动情况下,设计一个期权契约和成本共担收益共享联合契约,为LSSC的管理者和研究者提供启示:首先,物流服务水平影响需求变动会影响协调契约设计的效果;其次,物流服务成本系数对LSSC成员的决策有显著影响,随着成本系数增大,集成商的订购量减少,分包商愿意付出的努力减小;最后,由数值实验验证,在合理设计参数的条件下,本文提出的联合协调契约能够实现系统收益最大,保证LSSC成员共赢. 参考文献: [1] 崔爱平. 基于供应链契约的物流服务供应链能力优化与协调研究[D]. 上海: 上海海事大学, 2008. [2] DEMIRKAN H, CHENG H K. The risk and information sharing of application services supply chain[J]. Eur J Operational Res, 2008, 187(3): 765-784. [3] VÉRONNEAU S, ROY J. Global service supply chains: an empirical study of current practices and challenges of a cruise line corporation[J]. Tourism Manage, 2009, 30(1): 128-139. [4] CHO D W, LEE Y H, HWANG M K. A framework for measuring the performance of service supply chain management[J].Computers & Industrial Eng, 2012, 62(3): 801-818. [5] WEI Y H, HU Q Y, XU C. Ordering, pricing and allocation in a service supply chain[J]. Int J Production Econ, 2013, 14(4): 590-598. [6] GENOVESE A, KOH S C, ACQUAYE A. Energy efficiency retrofitting services supply chains: evidence about stakeholders and configurations from the Yorskhire and Humber region case[J]. Int J Production Econ, 2013, 144(1): 20-43. [7] 田宇, 吴佩勋. 物流服务供应链收益共享合同模型[J]. 科学管理研究, 2006(1): 227-229. [8] 刘伟华, 季建华, 顾巧论. 物流服务供应链两级合作的质量监控与协调[J]. 工业工程与管理, 2007(3): 47-51. [9] 崔爱平, 刘伟. 物流服务供应链中基于期权契约的能力协调[J]. 中国管理科学, 2009, 17(2): 59-65. [10] 桂云苗, 龚本刚, 张延龙. 考虑供应能力不确定性的物流服务供应链协调[J]. 北京交通大学学报, 2010, 11(2): 27-31. [11] 王晓立, 马士华. 供应和需求不确定条件下物流服务供应链能力协调研究[J]. 运筹与管理, 2011, 20(2): 44-49. [12] LIU W H, XIA D, XU X C. Quality supervision and coordination of logistic service supply chain under multi-period conditions[J]. Int J Production Econ, 2013, 142(2): 353-361. [13] 公彦德, 李帮义, 刘涛. 物流服务三级供应链定价及协调策略探讨[J]. 价格天地, 2008(9): 12-14. [14] 刘伟华. 三级物流服务供应链最优收益共享系数确定方法[J]. 西南交通大学学报, 2010, 45(5): 811-816. [15] 朱卫平, 刘伟, 高志军. 三级物流服务供应链能力协调[J]. 上海海事大学学报, 2012, 33(2): 26-32. [16] 赵正佳, 谢巧华. 供应链批发价与价格补贴的联合契约[J].管理工程学报, 2008, 22(4): 163-167. [17] KRISHNAN H, KAPUSCINSKI R, BUTZ D A.Coordinating contracts for decentralized supply chains with retailer promotional effort[J]. Manage Sci, 2004, 50(1): 48-63. [18] BOYER K K, HULT G T M. Extending the supply chain: integrating operations and marketing in the online grocery industry[J]. J Operations Manage, 2005, 23(6): 642-661. [19] LU J C, TSAO Y C, CHAROENSIRIWATH C. Competition under manufacturer service and retail price[J]. Economic Modelling, 2011, 28(3): 1256-1264. [20] 吴庆, 但斌. 物流服务水平影响市场需求变化的TPL协调合作[J]. 管理科学学报, 2008, 11(5): 64-75. [21] XIAO Tianjun, XU Tiantian. Coordinating price and service level decisions for a supply chain with deteriorating item under vendor managed inventory[J]. Int J Production Econ, 2013, 145(2): 743-752. [22] 王文, 刘伟. 生产性物流服务对制造企业市场竞争力因素的影响[J]. 上海海事大学学报, 2010, 31(1): 16-20. [23] 高志军, 刘伟, 朱卫平, 等. 客户企业奖惩下的LSSC安全和质量激励[J]. 上海海事大学学报, 2012, 33(3): 46-51.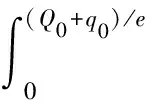
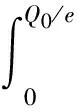
4.2 RF与S之间的成本共担收益共享契约

4.3 联合契约协调方法
5 算例分析
5.1 集中决策
5.2 Stackelberg博弈模型
5.3 联合契约协调
5.4 数值试验

6 结束语
——HeightsTM用高效率和智能化提升服务水平

