基于聚类分析的集装箱码头堆场策略
严伟, 朱夷诗, 黄有方, 何军良
(上海海事大学 集装箱供应链技术教育部工程研究中心, 上海 201306)
0 引 言
由于集装箱码头吞吐量的不断增加与码头规模的缓慢扩大相矛盾,制定合理的集装箱堆存规则,对提高堆场的利用率、周转率,提高码头服务效率显得尤为重要.严伟等[1]运用遗传算法对出口箱堆存问题建立箱区、贝位、箱位的堆放模型,并对双40英尺箱的堆存问题进行研究.候春霞[2]在考虑集装箱箱区分配的主要影响因素的基础上,以最小化集卡运输距离和最小化各箱区间工作量不平衡程度为目标函数对堆场策划问题进行建模研究.ZHANG等[3-4]研究预到达船中的出口箱存储空间和存储位置的分配.胡碧琴等[5]以内集卡和场吊效率最大化为目标,根据实际集装箱码头的堆存操作,提出相关限制条件.BAZZAZI等[6]运用遗传算法对堆场分配问题进行求解.
近年来,数据挖掘方法被广泛应用于各个科研领域,如:王天真等[7]利用k-means聚类的孤立点分析算法,从大量航运信息中挖掘AIS数据库中的异常信息;舒帆[8]提出基于空间信息和属性信息的可视化挖掘技术,并将其用在港口物流信息平台建设上;钮轶君等[9]研究数据挖掘在半导体制造管理中的应用;李小荣[10]详细介绍数据挖掘在企业历史数据中的主要应用;廉琪等[11]提出神经网络和粒子群优化的聚类组合算法,为制定策略提供帮助;NGAI等[12]研究数据挖掘在客户管理中的应用;KÖKSAL等[13]研究数据挖掘在质量改进中的应用.本文综合集装箱堆存模型的研究,结合堆场策划涉及的大量数据,考虑数据之间存在的复杂的相关性,通过确定各对象间的相异度提高数据间的独立性,在此基础上进行聚类分析.
1 问题描述
集装箱堆存计划可以分为进口堆存计划和出口堆存计划.进口堆存计划的制订相对简单,只要实际执行情况与堆存计划相吻合,卸船效率就能得到有效保证.但出口箱堆存计划的制订要相对复杂得多,以往的基本原则是以每条航线船舶的历次出口箱量及季节性浮动为基础预测箱量,预先对堆场进行适当规划,按照分类堆存策略为每艘船舶预留出口箱位置,集装箱实际进场时依此位置堆存.但实际作业中码头制订的堆存计划不可能准确地预测出口箱的进港顺序、箱型、重量和卸货港等信息,而且出口箱在集港过程中进箱时间分散且具有不确定性,但同一艘船上的出口集装箱又必须同时进行装船作业,所以在出口集装箱集港前必须给这些集装箱一个预先箱区堆存计划.以往用优化算法制定堆存策略时,大多以装船顺序已知作为假设或以有限个不确定条件为前提,例如,有些研究中将所有集装箱假定为20英尺箱、以最优的机械配置和船舶调度为前提、假定码头堆场资源(起吊设备等)充足等.有些集装箱并非完全严格按照堆存计划所规划的箱位进行堆存,而是按实际情况灵活调整某些箱位,从而导致某些堆存策略被忽略.
针对以上问题,本文提出基于数据挖掘的出口集装箱堆存计划,利用聚类分析方法发现隐藏于历史数据中有价值的信息,根据信息的相关性提取出口集装箱堆存规则.首先对大量历史数据进行筛选和清理,然后采用基于密度的聚类算法分析数据,最终给出较合理的堆放规则.通过对该问题的研究,可以获得以往不易被发现的隐藏在数据中的出口箱堆存规则,并将其应用于实际的堆场计划制订中,提高堆场效率.
2 数据选择和处理
2.1 影响因素分析
由于出口箱分散进港、集中装船,而且集装箱的进场时间和顺序存在很大的随机性,因此影响出口箱箱位分配的因素很多.本文主要考虑集装箱本身的属性和所处的物理位置.由于特殊箱量较少并有专门的堆放箱区,故本文不考虑特殊箱的堆存问题;由于出口空箱的堆放规则简单且对装船效率等影响不大,本文也不考虑出口空箱的堆存问题.本文主要分析出口箱较高级别的策划,即计划到区,对于集装箱的贝位计划和箱位计划所需考虑的翻箱率、场桥的分配个数、场桥大车的移动距离,本文不予考虑.
(1)集装箱箱型、尺寸:在制订集装箱堆存计划时,要按照不同的箱型进行总体规划,比如冷藏集装箱、框架箱、危险品集装箱等特殊箱都有专门的堆存位置,且堆放规则简单.在集装箱堆存时,经常会将集装箱的尺寸作为一个堆放条件,相同尺寸的集装箱堆放比较集中,不同尺寸的集装箱分开堆放,这样有利于提高场桥的利用率,也有利于装船作业的高效率完成.
(2)集装箱箱重:按箱重选取箱位可以避免船舶左右质量分配不对称,减少船舶产生横向倾斜的可能性,避免翻船.在为集装箱策划堆场位置时,集装箱装船后也要达到船身重心高度的优化.
(3)船名、航次:班轮运输有固定的航线、停靠港口和船期,故这两个指标可以确定集装箱的卸货港、装卸时间和该集装箱与其他集装箱的装船先后顺序.同船的集装箱堆放相对集中;同船、同一卸货港需将先装船的集装箱堆放在较顶层且相对集中;同船、不同卸货港的集装箱需间隔堆放.
2.2 数据选择
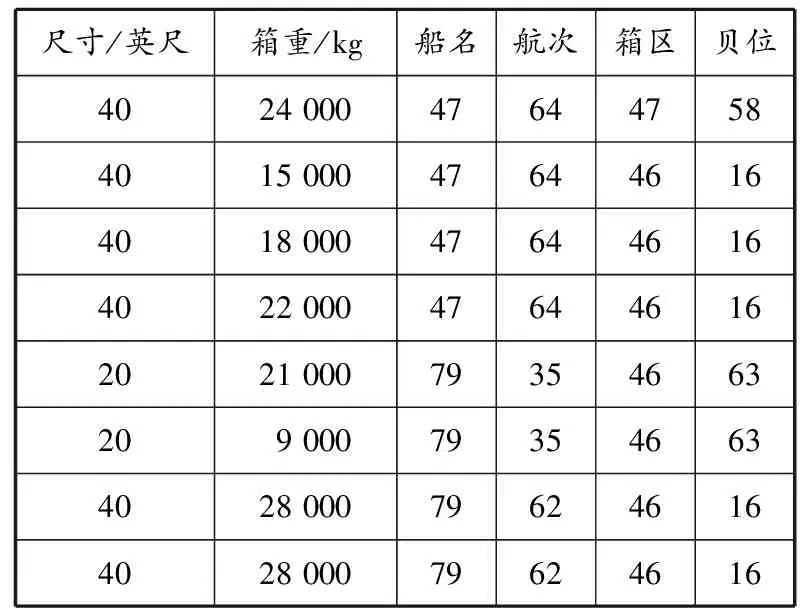
本文研究出口集装箱堆场策划问题,通过分析出口箱堆场策划的主要影响因素,选取集装箱尺寸、箱重、船名、航次为主要分析变量,但由于本文目的是通过分析历史数据得出集装箱堆放规则,故还应该选取集装箱所在箱区和贝位作为分析变量.用SQL对闸口集港报告、堆场数据表和堆场信息表进行连接查询,生成的新表结构示例见表1.
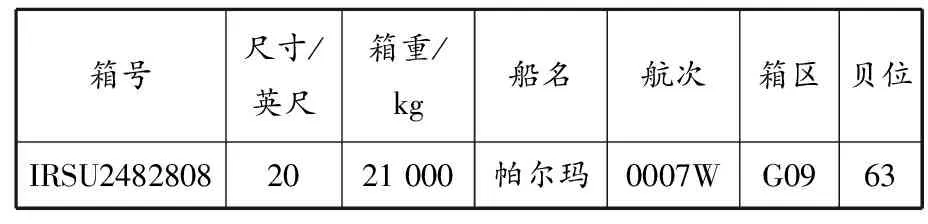
表1 新数据表结构示例
2.3 数据处理
为减少噪声和缺失值对聚类的影响,减少挖掘所需时间,对选择的数据进行缺失数据处理、删除噪声数据处理和数据离散化处理.
(1)缺失数据处理.本文所选取的数据表中缺失数据相对较少,为保证挖掘结果的质量,将缺失属性的个数超过3个的数据对象删除.本文主要采用选取固定常量替换缺失值和类比填充两种方法[14].
(2)删除噪声数据.出口箱信息预录的一种方式是直接用出口舱单作为预录信息,需要道口员根据装箱清单手工录入该箱的信息,在这种方式下集港的在场箱信息来自于舱单信息或道口员的手工录入.正是由于手工录入,所以可能产生人为的差错(包括孤立点值和错误的值).
(3)数据离散化处理.通过SQL语句查询分析可知,该数据表中总共有120个船名,用1~120进行编号(编号只是用于数据处理,并不代表任何特定的顺序或重要权衡).对船舶所对应的航次、集装箱所在箱区和贝位也作同样的预处理,这样此信息表将转换成一个完全由数字组成的初始数据矩阵.
通过以上处理,原来的表变成完全由数字组成的数据矩阵,为进一步分析奠定基础.
3 基于CADD的聚类
聚类的主要思想是:只要给定半径的邻域中的密度(对象或数据点的数目)超过某个阈值,就继续聚类.本文采用基于密度及密度可达的聚类算法(Clustering Algorithm Based on Density and Density Reachable,CADD).该算法不仅具有全局性的目标函数即密度值函数,而且可以有效减少噪声和孤立点的影响,对数据集的形状没有特殊要求,能发现任意形状的簇,对于复杂的聚类问题有很好的聚类结果.该算法的主要流程见图1.
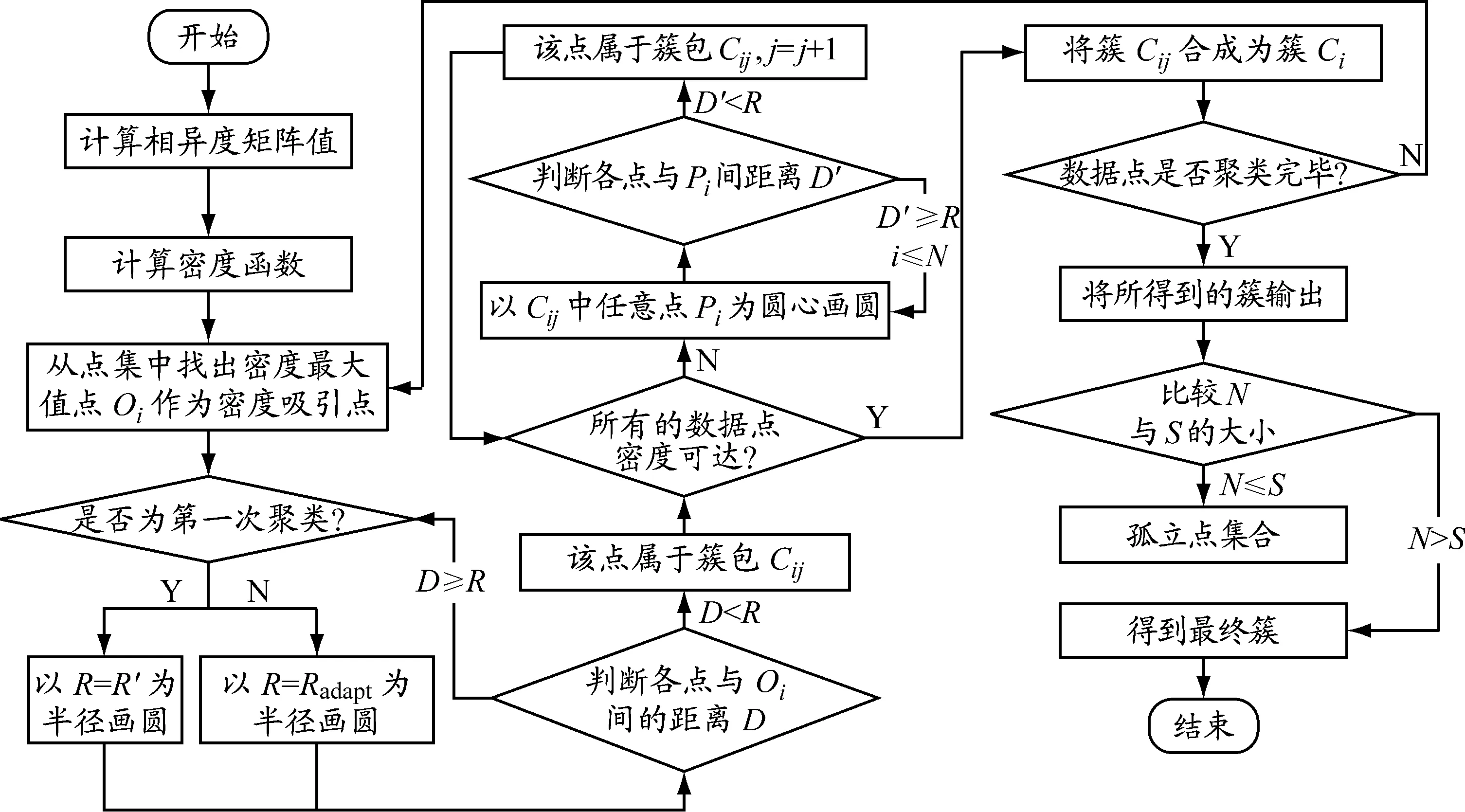
图1 CADD流程
图1中:R表示邻域半径;Cij表示第i个簇的第j个直接密度可达簇包;Pi表示Cij内的任意对象;Ci表示第i个簇,由Cij(j=1,…,j)组成;N表示簇中数据点的个数;S表示孤立点阈值.下面详细介绍各个变量及其计算方法.
3.1 相异度矩阵的计算
根据前面选取的聚类指标,将集装箱分割为有更多相似性的子群(或者簇),分割依据为集装箱之间的不同程度,即相异度.相异度用dij表示(i和j表示任意两个集装箱),各个相异度取值在0和1之间,取值越大,集装箱的属性越不相似,取值越小集装箱间的相似度越大.当i=j时,dij=0.为计算各个集装箱间的相异度,选取集装箱的6个属性作为分析变量,其中:尺寸有20英尺、40英尺和45英尺3种,为分类变量;箱重的取值是趋于连续的,从5 000到30 000不等,所以箱重为区间标度变量;船名、航次、所在箱区和所在贝位是分类变量,包含几种不同变量类型的集装箱间的相异度应该按照混合类型变量计算.集装箱的个数为7 500个,所以i和j均从1取值到7 500,那么可以得出一个7 500×7 500相异度矩阵.各集装箱间的相异度计算方法为
(1)
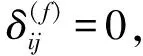
(1)根据箱重计算相异度为
(2)
式中:max(xhf)和min(xhf)为取遍所有箱重不为0的对象的最大值和最小值,因为只有箱重属性为区间标度变量,无须进行标准化处理,所以max(xhf)和min(xhf)可以看成是两个常量.
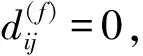
3.2 密度函数的计算
相异度值代表的是任意两个集装箱间的相异程度,不能从整体上描述集装箱间的相异度.从全局的角度衡量各个集装箱间的相异度可以采用密度函数值.某个集装箱的密度函数值由该集装箱与所有集装箱间的相异度共同决定.集装箱的密度值为所有集装箱对该集装箱的影响函数的总和.密度函数为
(3)
(4)
式(4)为高斯函数,表示每个集装箱对第i个集装箱的影响;σ为密度参数,σ∈[0,1],决定密度函数的变化梯度.计算结果应该是一个7 500×1数据矩阵.密度矩阵中的每个值与每个集装箱一一对应,这样集装箱分类问题就转换成数学问题,即通过密度函数值进行分类.
3.3 邻域半径的确定
根据CADD确定数据对象的密度吸引点(密度最大值点)后,根据指定的全局邻域半径确定直接密度可达包.全局邻域半径为
R′=M·CR
(5)
式中:M为所有数据对象的平均距离;CR是邻域半径的调节系数.
在σ不变的前提下,在密度值较大的局部密度吸引点所代表的簇中,数据对象间的密度可达距离较小;而在密度值较小的局部密度吸引点所代表的簇中,数据对象间的密度可达距离较大.也就是说,在聚类过程中对于不同密度的簇,密度可达距离是变化的.因此,在聚类过程中可以定义自适应密度可达距离为
(6)
式中:D(Ai)和D(Ai+1)分别为先后确定的两个簇密度吸引点的密度值.
3.4 局部密度吸引点及局部密度
(1)局部密度吸引点是数据点密度的局部最大值点.其计算公式为
Oi=max{D(i),i=1,2,…,N}
(7)
(2)对于给定的邻域半径,计算每个数据点邻域内的密度,也就是仅仅考虑数据点邻域内点的影响.如果数据点的邻域内的点最密集,那么对应的密度必然全局最大,故可将其作为密度中心点.
3.5 密度可达及简介
(1)密度可达对象.如果存在一个对象链p1,p2,…,pn,pn=q,q是一个局部密度吸引点,那么对于pi∈D(1≤i≤n-1),满足dis(pi,pi+1) (2)间接密度可达对象.对于数据对象链p1,p2,…,pn,pk=q,设q是一个核心对象,其邻域内的点链为dd1,dd2,…,ddm,其邻域外的点链为pp1,pp2,…,ppn-m,如果某ppj满足式(8),那么称ppj为q的间接密度可达对象,式(9)为两对象间的距离. dis(ppj,ddi) (1 (8) dis(ppj,ddi)=|D(ppj)-D(ddi)| (9) 在相异度矩阵、对象密度值、邻域半径确定之后开始进行聚类.在聚类前要对孤立点阈值(大于0的任意正整数)进行设定.孤立点阈值的选取是为满足算法在寻找密度中心点到非常稀疏的某些数据区域中的数据点的距离时,如果密度中心点的间接密度可达包内包括的数据点个数小于给定的阈值,那么就将这些点划分为孤立点. 原始数据通过前面的数据准备、数据选择、数据清理和数据预处理后,数据范围有效缩小.本文数据挖掘中进行聚类的对象共计7 500个,包括6个属性值.对集装箱箱重、船名、航次、所在箱区、所在贝位的区间离散化和编号处理之后,得到一个新的数据表,构成要进行聚类分析的数据矩阵,作为输入的原始数据对象集,表2列出部分数据. 表2 初始数据矩阵 CADD中有3个参数:σ,CR和S.参数的取值对聚类结果和聚类的质量有很大的影响,本文所举实例的参数设定过程如下: (1)σ从1开始取值,如果大多数数据点密度值接近1或7 500,需改变σ的取值,避免选取的σ使数据对象密度值接近于1或7 500. (2)CR∈[0,1),先从1开始选取,然后依次减小,直到取0为止.通过观察聚类结果、结果簇的数目和密度吸引点选取CR,使结果簇的数目适中. (3)预设定S上限为对象个数的3%,即为23个,下限为3个,那么在聚类时S在3到23之间取整数即可,通过观察聚类结果最终确定S. 通过反复调节参数值,观察结果簇的特性,最终确定CR=0.001 5,σ=1,S=10.经过执行算法程序,得出相异度矩阵、对象密度函数值、各个簇的密度吸引点和每个簇中对应的对象编号,利用Powerbuilder 11.5进行编程实现该算法.程序执行结果见表3. 表3 结果簇 通过以上程序的计算得出的14个簇中有3个簇的对象个数小于给定阈值10,C1,C2,C3中对象个数均为1,故将其划分为孤立点簇. 衡量港口的效率和顾客满意度的指标有两个:(1)船舶停港时间最小化,为船舶服务的指标;(2)港口设备利用率最大化,为衡量港口生产率的指标.堆场空间资源配置的目的是提高上述两个指标,通过在SQL 2000的查询分析器中对数据分析表进行查询统计分析,得到的集装箱分配策略见表4. 表4 集装箱分配策略 表4中:(1)船型A,B,C,D,E对应5种不同的装载量等级,装载量和装箱量依次递减;(2)所在箱区表示计划箱堆存的某个箱区;(3)船型是经过数据处理、根据装载量得出的;(4)箱重范围是该类船型集装箱的平均箱重范围;(5)20(或40)英尺箱数量表示该船舶同一航次中20(或40)英尺集装箱的数量范围,此为作业量;(6)箱区1~6没有固定位置的含义,只代表不同的箱区,箱区的位置按预装船舶的泊位位置而定.按此规则为即将集港的集装箱预先分配箱区,箱区的位置可以根据船舶的靠泊位置确定. 采用由Tecnomatix公司开发的eM-Plant 9.0对上述集装箱分配策略的实用性进行仿真验证.对原始方案和该方案的机械设备水平运输距离和装船时间两个指标进行对比.仿真数据采用某集装箱码头3天内到港的船舶.该码头共有5个泊位,码头部分平面布局见图2,数据内容见表5. 图2 码头部分平面布局 表5 3天内到港船舶的出口箱数据 运行集装箱堆场策划仿真模型,将记录的实际堆场策划方案结果与聚类分析得出的方案在堆场策划仿真系统中得出的结果进行对比,结果见表6. 表6 原方案与现有方案对比 从表6可以看出,采用现有方案后各项指标都有所改进,总装船时间从85.12 h减少到76.06 h,减少10.64%;装船时,机械设备的水平运输距离从13 415.6 m减少到11 816.4 m,减少11.92%. 对集装箱码头堆场的历史数据进行深入研究,对某集装箱码头某时段内的集装箱分配进行聚类分析,并建立基于密度及密度可达算法的聚类模型,得出出口箱堆场堆存方案.该方案可为码头制订出口箱堆存计划提供帮助,更为今后研究堆场策划等规划调度问题拓展思路.通过仿真分析,将得出的规则应用到实际堆场策划中可提高堆场的效率、减少设备的水平运输距离和装船时间. 参考文献: [1] 严伟, 谢尘, 苌道方. 基于并行遗传算法的集装箱码头堆场分配策略[J]. 上海海事大学学报, 2009, 30(2):14-19. [2] 候春霞. 集装箱码头出口箱堆场空间分配研究[D]. 大连:大连海事大学, 2011. [3] ZHANG Yanwei, ZHOU Qiang, ZHU Zongming,etal. Storage planning for outbound container on maritime container terminals[C]//Automation and Logistics, 2009 IEEE Int Conf IEEE, 2009: 320-325. [4] ZHANG Yanwei, MI Weijian, CHANG Daofang,etal. An optimization model for intra-bay relocation of outbound container on container yards[C]//Automation and Logistics, 2007 IEEE Int Conf IEEE, 2007: 776-781. [5] 胡碧琴, 江伟. 基于限制条件的港口集装箱码头出口集装箱堆存定位研究[J]. 物流科技, 2010, 33(12): 15-19. [6] BAZZAZI M, SAFAEI N, JAVADIAN N. A genetic algorithm to solve the storage space allocation problem in a container terminal[J]. Computers & Industrial Eng, 2009, 56(1): 44-52. [7] 王天真, 刘萍, 汤天浩, 等. 一种基于k-means 聚类的航运信息孤立点分析算法[J]. 上海海事大学学报, 2011, 32(3): 54-57. [8] 舒帆. 港口物流信息平台共享架构及其可视化挖掘[J]. 上海海事大学学报, 2006(S1): 79-84. [9] 钮轶君, 钱省三, 任建华. 基于数据挖掘的半导体制造质量异常研究[J]. 半导体技术, 2006, 31(12): 892-895. [10] 李小荣. 数据挖掘在企业历史数据中的应用[J]. 中国管理信息化, 2011(2): 51-52. [11] 廉琪, 苏屹. 基于SOM和PSO聚类组合算法的客户细分研究[J]. 华东经济管理, 2011(1): 118-121. [12] NGAI E W T, XIU L, CHAU D C K. Application of data mining techniques in customer relationship management: a literature review and classification[J]. Expert Systems with Applications, 2009, 36(2): 2592-2602. [14] 金勇进, 邵军. 缺失数据的统计处理[M]. 北京:中国统计出版社, 2009: 1-80.3.6 孤立点阈值的确定
4 案例分析
4.1 初始数据集
4.2 参数选择
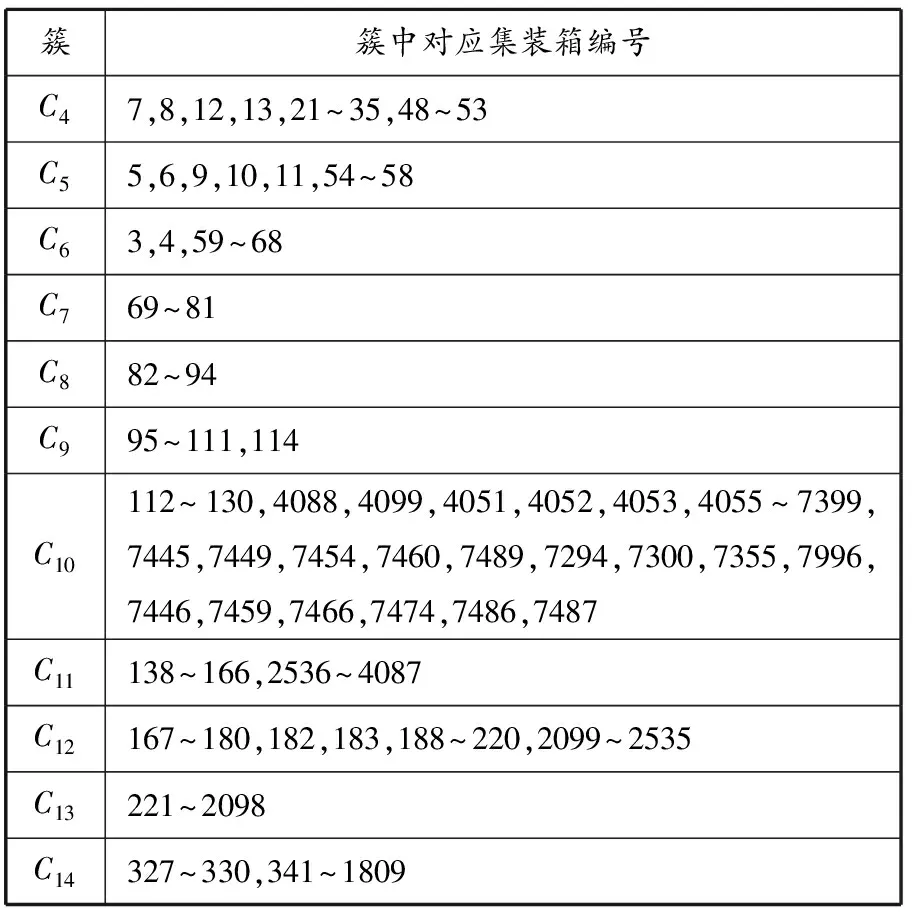
4.3 计算结果
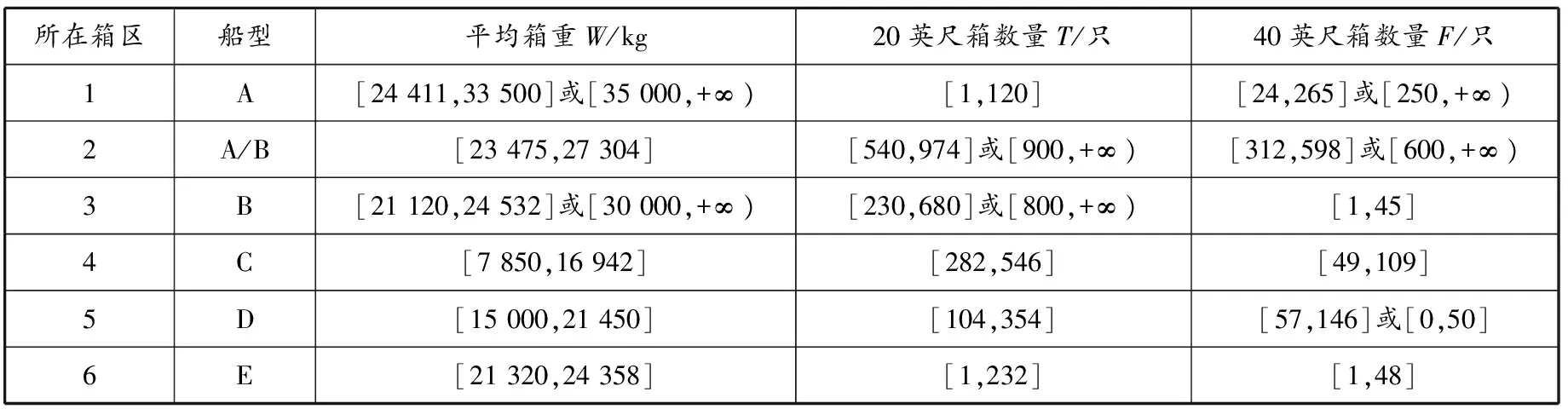
4.4 仿真分析
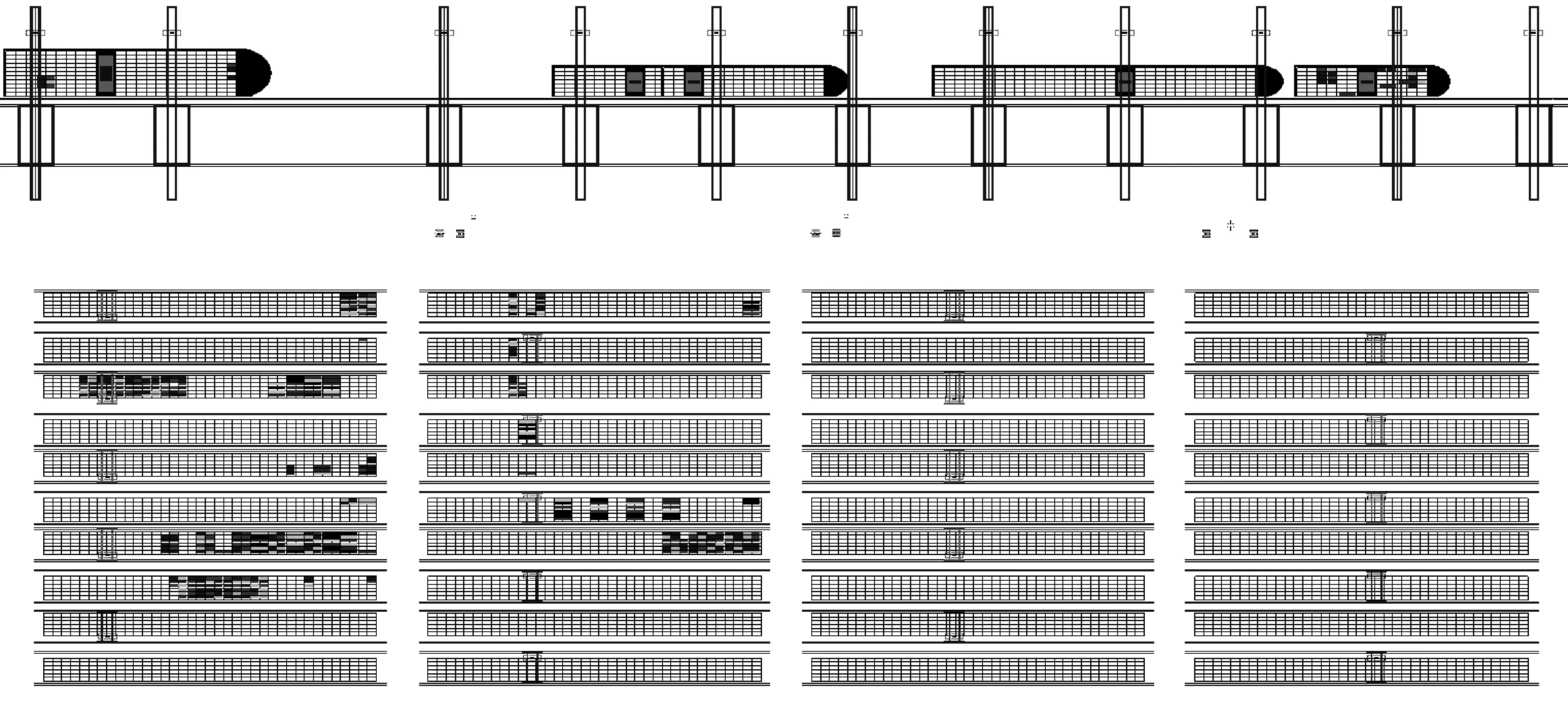


5 结束语


