耙吸挖泥船耙头密度估计器研究与分析
王柳艳,田雨,俞孟蕻
(1.江苏科技大学电子信息学院,江苏 镇江 212003;2.长沙理工大学,湖南 长沙 410114)
耙吸挖泥船耙头密度估计器研究与分析
王柳艳1,田雨2,俞孟蕻1
(1.江苏科技大学电子信息学院,江苏 镇江 212003;2.长沙理工大学,湖南 长沙 410114)
针对新型耙头的挖掘模式,利用黑箱模拟法与在线滚动优化预测理论,设计了一种耙头吸入密度估计器,采用现场实测数据进行了仿真实验。结果表明,该密度估计器可以较为准确地预测耙头底部的吸入密度,在疏浚作业中实时提供连续的混合物吸入密度信息,及时指导操作人员针对不同工况调整疏浚参数,满足高效疏浚的需求。
耙吸挖泥船;耙头密度估计器;黑箱模拟法;滚动优化预测
0 引言
耙吸式挖泥船在疏浚时耙头的吸入产量随挖掘地点土质的变化而不断变化,而很多土质特性是无法测量或难以测量的。因此本文利用非线性数据驱动的黑箱模拟法结合递推最小二乘法在线估计设计了一种耙头吸入密度估计器。
1 耙头疏浚机理分析
耙头是挖泥船的重要机具,其任务是挖掘河道底部的沙石、淤泥,然后由泥泵通过管道将吸入的泥水混合物输送到泥舱中。
耙头吸入混合物的总产量与挖掘模式有关[1]:
1) 传统的冲刷型耙头冲刷后通过泥泵和管线吸入耙头底部的泥沙混合物。
冲刷型耙头破土性能较低,仅由泥泵和管线吸水时产生的水流对耙头底部的泥沙冲刷挖掘。
2) 挖掘型耙头:由切割(或辅于高压冲水)挖掘后由泥泵和管线吸入耙头底部的泥沙混合物。
耙头由刀片、耙齿、高压冲水装置组成,河道底部淤泥通过切割和高压冲水后被输送到泥舱。现代大型耙吸挖泥船均装备挖掘型耙头,耙头挖掘过程见图1。
主动耙头与挖掘深度 hs和耙头活动罩(泥罩)入土纵深 hz之间的关系有以下 3 种情况:
1) 当 hs=hz时,挖掘深度 hs等于泥罩纵深hz,此状态下耙头工作最有效。
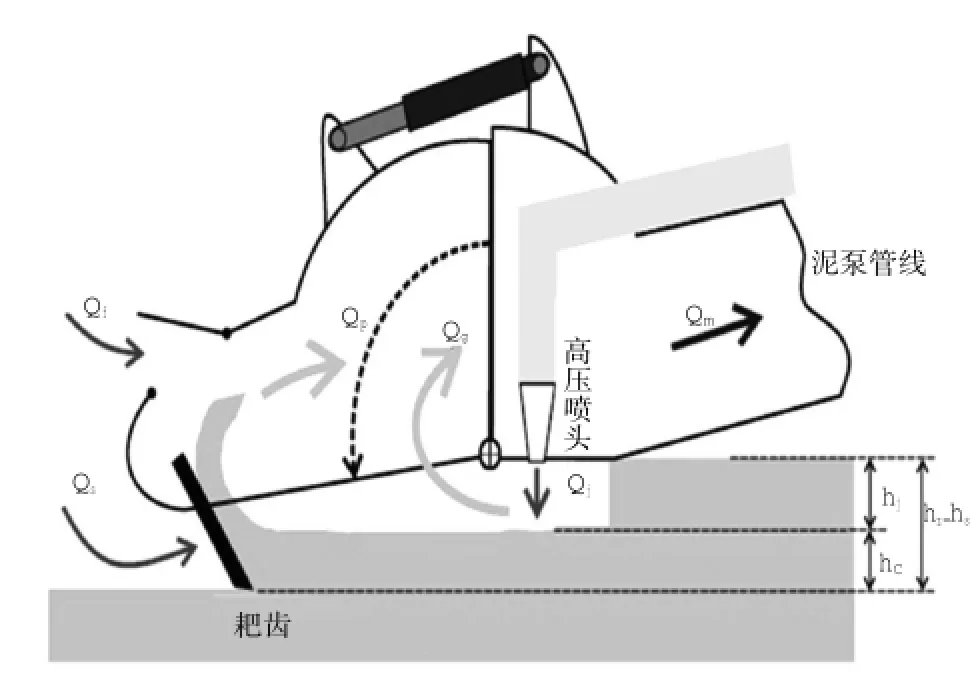
图1 耙头挖掘过程示意图Fig.1 Sketch of the drag-head during the excavation regime
2) 当 hs>hz时,耙头底部和跟部之间没有空隙。这种情况下无切削产生,这意味着整个吸入产量完全是通过高压冲水获得。
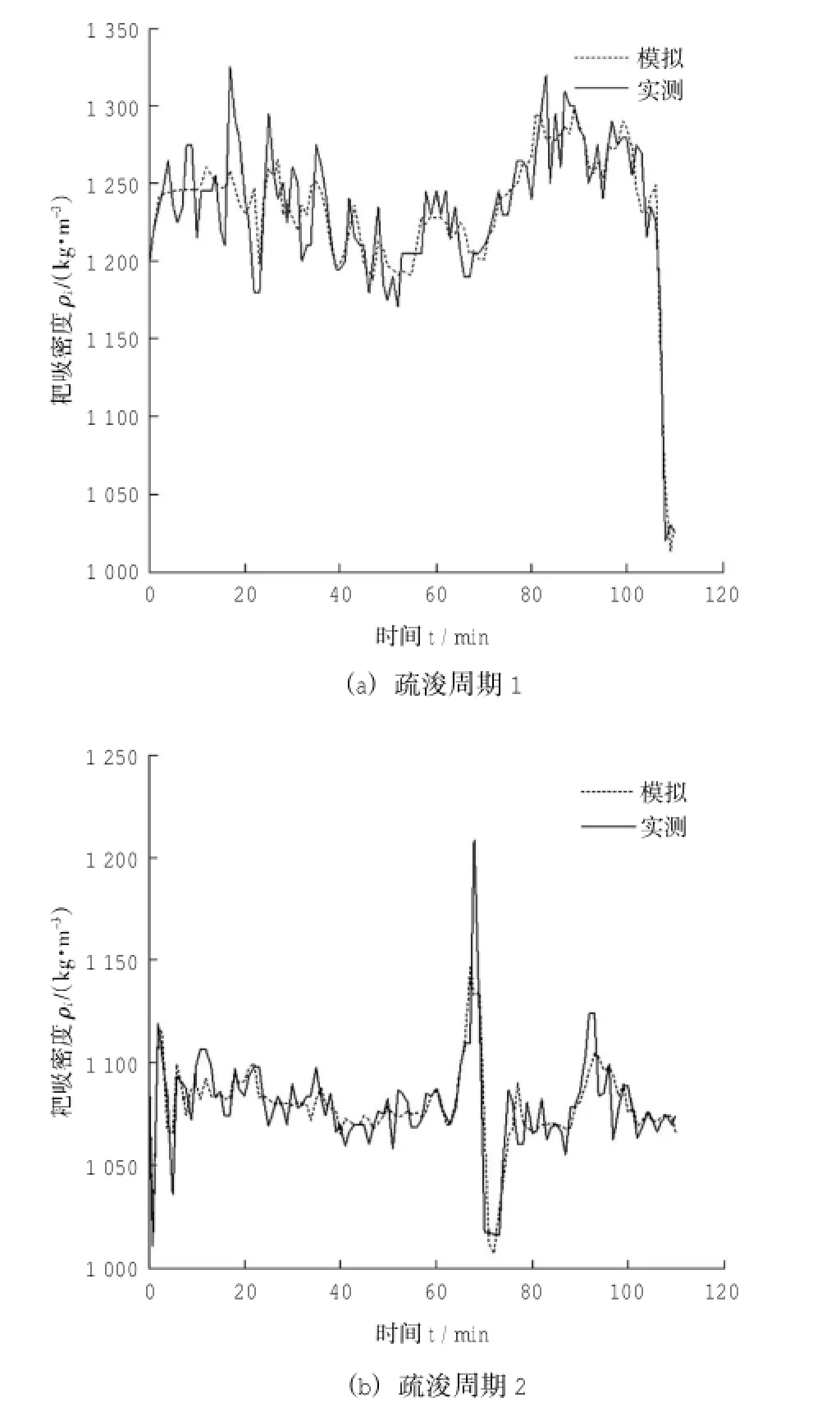
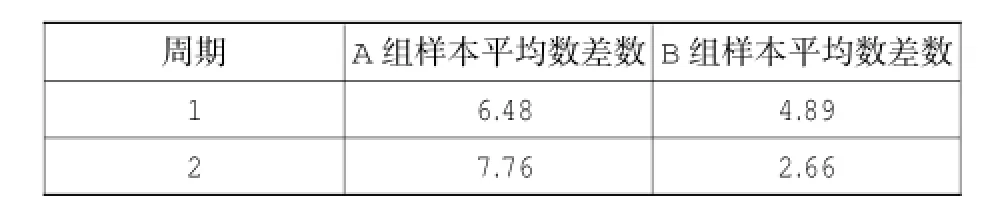
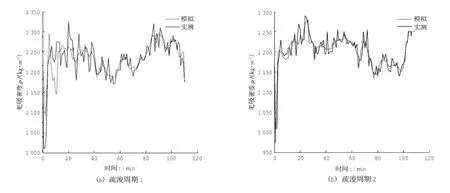
3) 当 hs 在本论文中,将对无间隙挖掘过程作分析。 耙头挖掘过程中可建立如下体积平衡关系式: 式中:Qm为左右 2个耙头各吸入混合物流量;Qp为耙齿切割时产生混合物供应量;Qg为高压冲水时松动土壤(砂)供应量;Qj为高压喷头产生的流量;Qa为周围的水流量;Qf为通过阀门的流量。 耙头的吸入流量来自于 Qp和 Qg,并且这两个量与喷射深度 hj、切削深度 hc、船的速度 vsh和耙头的宽度Wd有以下关系: 式中:Wd为已知的参数;vsh可测量得到。 2.1 经典模型 由耙头的疏浚机理可建立耙头模型,通过耙头模型可以估算吸入密度来预测吸入的产量。由耙吸挖泥船的传感器可测量得到吸入流量、航速、活动罩角度等变量的数据,泥泵转速控制吸入流量的大小。但耙齿的切割、高压冲水和水流冲刷之间的作用力通常无法测得,水下土壤密度也是未知可变参数。 针对模型的输入-输出机理,本文通过非线性数据驱动黑箱模拟法对耙头密度进行建模,引用多项式模型如下[2]: 式中:Qi为进舱流量;vsh为对地航速;ρi为耙头吸入密度;adh,bdh,cdh为模型中需估算的参数。 针对这一多项式,利用安装在耙臂上的流量计和密度计可以测得 Qi和 ρi,从而对上式进行仿真估计[3]。 3个参数的估算将通过实测数据用最小二乘法计算得到。 2.2 估算参数分析 考虑此参数估计问题是线性的,可以使用最小平方算法求解[4]。需求解的线性方程组 如下: 若将 tij记作数据矩阵 A ,A 为输入参数;参数 aj记作参数向量 b,b 为预估参数;观测值 yi记作y,为输出变量。则线性方程组为: 此方程组的二范数极小解的计算方法为: 2.3 耙头密度估计器研究分析 依据已建立的耙头产量模型方程式,并采用实际疏浚数据,对模型中的未知参数 adh,bdh,cdh进行了估计预测。但以往的研究都是将此参数估计值设为定值提供给疏浚优化控制系统,这样不仅没有在一个疏浚周期内准确预测到不断变化的吸入密度,也制约了优化控制系统的性能。 因此,对耙头吸入密度准确估计采用以下工作步骤: 1)滚动优化 由于实际疏浚过程中每个时间段采集若干组输入-输出数据,因此为了预测耙头吸入密度 ρi的准确性,优化其估计性能,针对测得数据每10组做 1 次 adh,bdh,cdh的参数估算,将最新的估计参数运用到公式 (4) 中,再循环进行下一组的吸入密度预测。每次仿真取一个疏浚周期中 100 组数据进行测试。这样滚动进行的实时预测不仅提高了预测的准确性,还为后续的疏浚性能评估提供了依据。 2)耙吸管道的延迟补偿 考虑到 Qi, ρi不是在耙头的进口处测得,而是在泥泵处由流量计和密度计测量所得,因此所测得的密度值具有约数秒的延迟。为了弥补此延迟,所以期望下个时间段的 ρi,mens(k+ τ)为: 式中:τ为样本延迟;k为时间指数。 但 ρi,mens(k+ τ)是未知的,可以计算前一个密度值,即 ρi,mens(k): 由于带入延迟 τ 的不同,预计 ρi,mens(k)也在变化,这里将通过计算预测和实测值的方差,寻找到τ=3时的密度估计达到最佳状态。 3) 性能评价 耙头密度估计器设计完成的同时还需确定一个性能指标来评价模型的性能。本文采用计算实测值和预测值2组数据的平均数差数的标准差来做性能评价,称为“数据差异显著性检验”[5]。这种检测方式可以明显针对2组的差异性进行检验,比较出每组调整后预测值的准确性,今后可利用预估的参数做具体分析并提高耙头挖掘效率。 样本平均数差数的标准差计算公式(2个样本个数相同时): 4) 利用 MATLAB 设计仿真耙头密度估计器 根据实际数据的输入轨迹和初始条件来做出模型的预测仿真,运用 MATLAB 仿真耙头密度估计器。 本次仿真实验使用了不同挖泥船在不同工况下的数据:挖泥船A在河北某港和挖泥船B在福建某港的实测数据对耙头密度估计器模型进行实验。在性能指标评价的A、B两组数据分别选取2个工况中的 2 个疏浚周期样本为 100 组点性样本作比较。 验证方法:将耙头密度估计器的密度估计值与船上安装的密度计测得的实际密度值进行比对,通过仿真图和数据验证此密度估计器的精准度。 1) A 组数据仿真结果 选取 2014 年 4 月 8 日,挖泥船 A 在河北某港作业时其中的 2 个疏浚周期中的 100 组数据进行仿真实验,当时航行平均速度在 4 kn 左右。 从以下仿真图可以看出在河北某港疏浚周期中预估吸入密度与实测密度的趋势走向较为吻合。比较每次疏浚过程中吸入的混合物平均密度有所不同,如图 2(a)所显示的平均吸入密度在 1 200~ 1 300 kg/m3之间,图 2(b)所显示的平均吸入密度约在 1 050~1 100 kg/m3之间。 图 2 耙吸密度 ρi在 A 组数据下预测和实测结果Fig.2 Drag suction density ρipredicted and measured results under A group of data 由仿真图可以看出:在耙头吸入密度有较大改变之前,此密度估计器可以较为准确的预测耙头密度的变化趋势。 从表 1A 组样本平均数差数可见耙头模型预估吸入密度结果表现良好,数据平均数差数的标准差也较小。这说明此耙头密度估计器可以用于黄骅港土质的预测,且预测较为准确。 表1 预测值与实测值的差异性检验Table1 Differences between the predicted and measured values of test 2) B 组数据仿真结果 第二个工况为 2014 年 6 月 2 日在福建某港使用挖泥船B进行疏浚时测得其中2个疏浚周期中的 100 组数据对模型进行仿真分析。当时平均航速在 3 kn 左右。 图 3 耙吸密度 ρi在 B 组数据下预测和实测结果Fig.3 Drag suction density ρipredicted and measured results under B group of data 通过以上仿真图可看出在福建某港的疏浚作业中预估吸入密度与实测密度的变化趋势基本相同,且当每次疏浚过程中吸入的混合物平均密度有 所 不 同 时 , 如 图 3(a)所 示 的 平 均 吸 入 密 度1 200~1 260 kg/m3之间, 图 3(b)所显示的平均吸入密度约在 1 150~1 250 kg/m3之间,可见在不同的疏浚周期中针对吸入混合物密度有较大改变时也能较为准确的预测耙头吸入密度。从表 1B组样本平均数差数可见预测值与实测值的差异较小。 比较仿真图 2、图 3时发现 B 组吸入密度的平均值比A组要小,实际为B组在疏浚时打开了高压冲水装置,且航速较第一个工况也小,从而吸入密度变小。通过第二组工况实验验证此耙头密度估计器在福建某港下的数据预测仿真结果比较好。 本文在耙头挖掘过程中耙头密度估计器的实现可以在管道的进口处预测出在后续疏浚周期中实时的吸入密度。通过此密度的确定,结合其他控制器的操作,工作人员可以调整泥泵转速、航速、活动罩角度等来提高耙头部分的疏浚效率。 [1] PAWEL M STANO.Nonlinear state and parameter estimation for hopper dredgers[M].Netherlands:Pawel Miroslaw Stano,2013: 8-9. [2]WANG Li.Intelligent data analysis and control of a hopper dredger [D].Netherlands:Delft University of Technology,2006:42,79,169. [3]MAERTENS K,BABUˇSKA R,BAERDEMAEKER.Evolutionary input selection for the non-linear identification of complex processes[J].Computers and Electronics in Agriculture,2005,49(3): 441-451. [4] 杨世兴,张宝泉,赵永秀.MATLAB 在最小二乘参数辩识中的应用[J].电工技术,2003(11):44-45. YANG Shi-xing,ZHANG Bao-quan,ZHAO Yong-xiu.Application of MATLAB in the least-squares parameter identification[J]. The Electrician Technology,2003(11):44-45. [5] 张凤菊,刘晓娟,赵丽平,等.数据差异性显著检验[J].农机使用与维修,2012(4):51-52. ZHANG Feng-ju,LIU Xiao-juan,ZHAO Li-ping,et al.Significant differences in test data[J].Agricultural Use and Repair,2012(4): 51-52. Research and analysis on drag head density estimator of trailing suction hopper dredger WANG Liu-yan1,TIAN Yu2,YU Meng-hong1 Based on the new type drag head of digging model,we used the black-box simulation and online rolling forecast to design a drag head density estimator,and carried the simulation experiment with field data.It proved that the estimator can accurately predicting the inhalation density,can provide continuous real-time to the operators when the density of the mixture inhaled dredging,can let the operator according to different working conditions to adjust each subsystem,and can meet the efficient dredging requirements. trailing suction hopper dredger;drag head density estimator;black box simulation method;rolling optimization forecast U674.31 :A文献标志码:2095-7874(2014)11-0069-04 10.7640/zggwjs201411020 2014-09-25 2014-10-21 航道疏浚技术交通行业重点实验室基金资助项目 (7200603023) 王柳艳 (1990 — ),女,江苏溧水人,硕士研究生。从事耙吸挖泥船高效化疏浚课题研究。E-mail:wangliuyanxx@163.com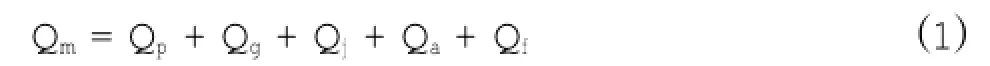

2 耙头吸入密度器的研究方法

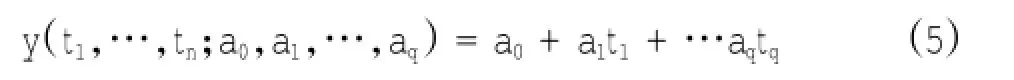


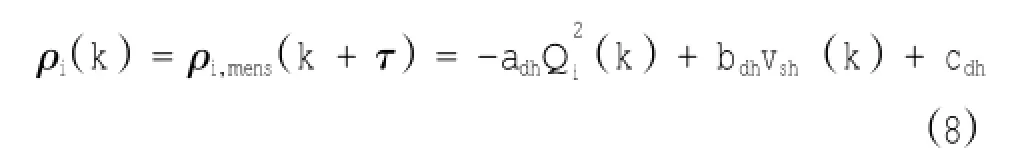
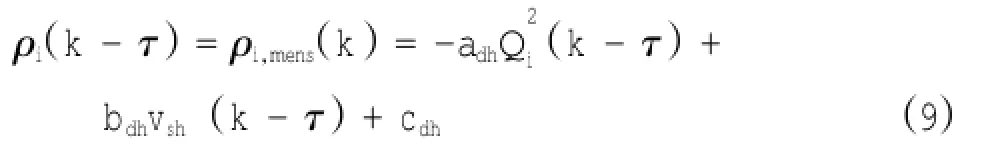

3 耙头密度估计器的仿真与验证
4 结语
(1.School of Electronics and Information,Jiangsu University of Science and Technology,Zhenjiang,Jiangsu 212003,China; 2.Changsha University of Science&Technology,Changsha,Hunan 410114,China)

