一种基于最优输出跟踪的多源动态载荷识别方法

陈 睿, 刘 杰, 张 正, 张 伟

(1. 湖南大学汽车车身先进设计制造国家重点实验室，湖南 长沙 410082；2. 吉首大学物理与机电工程学院， 湖南 吉首 416000 )

引 言

在机械、结构系统的力学计算、结构设计、故障诊断中，载荷的确定是一个非常重要的问题，它为结构的设计、计算以及分析提供可靠的载荷依据，为减小振动、提高结构的可靠性、安全性，提供确切的环境条件。然而在很多实际工程中，如导弹及航天器在飞行时的载荷、发电站工作时机组及脉动水压力、桥梁所受运动态载荷等，由于技术条件或经济条件，对结构所受外载荷难以直接测量甚至根本无法实测。因此，近年来基于结构测取的响应识别结构所受外载荷的技术取得了很大的进步。

载荷识别在结构动力学中属于第二类反问题，它根据已知系统的动态特性和实测的动力响应反求出结构所受的动态激励。动态载荷识别的研究最早可追溯到20世纪70年代末，从军事用途发展起来的[1]。目前动态载荷识别的方法主要有频域法和时域法两大类方法[2,3]。频域法发展较早，是比较成熟的识别方法，其应用较为广泛。该方法动态标定简单、识别精度较高，但要求测试数据的样本具有一定的长度，一般只适用于稳态或平稳随机载荷识别，对冲击型瞬态载荷的识别则受到限制。时域法提出较晚，它从系统动力学方程出发，根据响应的时间历程直接确定动态载荷的时间历程。时域法直观，广泛应用于工程中，其优点在于时域法可对非平稳动态载荷识别，对冲击型载荷识别更是具有实际工程价值。目前国内外已开展了广泛研究，并取得了一定的成果[4～6]。

本文从系统动力学方程出发，基于最优输出跟踪的基本思想，在载荷位置确定的基础上，通过实测的动力响应反求出结构所受的动态载荷。该方法针对集中力载荷，实现了多源动态载荷识别，并采用L曲线法确定了最优输出跟踪中性能指标的关键参数。数值算例结果表明了本文提出的基于最优输出跟踪的动态载荷识别方法的有效性和可行性。该方法在载荷作用的全部时间域内整体进行反求，应用方便，计算量较小且效率较高，并具有较强的抑制噪声能力。

1 载荷识别的正问题

结构动力响应的有限元离散形式为[7]

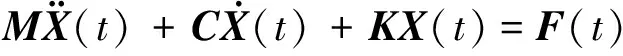
(1)

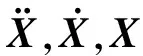
可将式(1)改写为

(2)

假设一空间向量

(3)

建立相应的系统方程

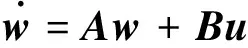
(4)

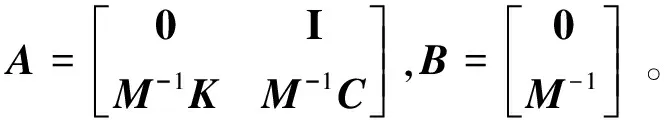
该系统结构响应的输出为

y=Dw

(5)

若实际测点响应量为z，(z=[z1z2…zn]，n为测点个数)。该响应可以为位移响应或速度响应。如果实测响应量z已知，需求结构的外载荷，就转化为最优跟踪问题，即寻求最优控制u，使得结构响应输出y(t)尽量跟踪上已知实测的响应输出z(t)。

记e为跟踪误差，即

e(t)=y(t)-z(t)

(6)

2 基于最优输出跟踪的载荷识别

最优输出跟踪问题是寻求一种最优控制，既能保证跟踪误差尽可能小，又要避免使用取值“过大”的控制，故选用下式的最优化性能指标[8]

(7)

式中t0为起始时间，tf为终止时间，f表示末值型性能指标参数，Q表示平均误差度量性能指标参数，R表示最小能量控制参数，且∀t∈[t0,tf],f≥0,Q≥0,R>0。本文假设这些性能指标参数都为常数。

由于载荷识别问题中结构的外载荷是肯定存在的，所以肯定存在最优控制。本文的载荷识别方法基于载荷位置已知，并通过实测获得测点的响应来反求载荷。此外，该载荷识别问题注重时间历程，对终端误差不关注，进而可忽略终端响应量的误差，即令f=0。因此，最优性能指标式(7)可改写为

(8)

式中r=R/Q。

从式(4)和(8)易知哈密尔顿函数为

λTAw+λTBu

(9)

u*(t)=R-1BTλ

(10)

由极大值原理知共轭方程和横截条件分别为

λ(tf)=0

(11)

将式(10)代入式(4)并结合式(11)得正则方程和端点条件

(12)

根据式(12)，可以假设

λ(t)=-p(t)w(t)+g(t)

(13)

微分式(13)并结合式(12)得

(14)

将式(13)代入式(11)，并联合式(14)得

p(t)BR-1BTp(t)]w(t)+[p(t)BR-1BT-

(15)

由于式(15)对任意w(t)均成立，利用w(t)的任意性可知，p(t)和g(t)分别满足

(16)

由式(11)及w(tf)的任意性得

p(tf)=0，g(tf)=0

(17)

从而可以得到最优跟踪器为

(18)

进而得到最优跟踪器相应的响应

(19)

因此，要最终求得最优跟踪器u*(t)，即结构所受的外载荷，就要求解式(16)和(17)，即带终端条件的Riccati微分方程以及带初始条件的微分方程(19)。

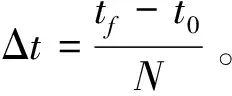
通过上述方法求解微分方程求得p,g,x，即可求出最优跟踪器，即结构所受的外载荷u*(t)。

3 L曲线法确定关键性能指标参数

利用上述方法进行载荷识别过程中，需要确定最优化性能指标中的指标参数，即式(8)中的权重系数r。当测量响应中存在误差时，跟踪误差和所获得的取值都会不同程度的变化，因此该权重系数r=R/Q的选取至关重要，既要保证跟踪误差尽可能小，又要避免取值“过大”。为了能有效地确定r值，本文采用适应性强的L曲线法以获取最佳的r值。

L曲线法是指用对数尺度来描述残差范数和解的范数的曲线对比[10]，该方法的典型特征是尺度图形中出现一条明显的L曲线，曲线的拐点所对应的参数当作优化参数。式(8)中eT(t)e(t)和uT(t)u(t)都是权重系数r的函数，选择不同的r值，以eT(t)e(t)的对数为横坐标，uT(t)u(t)的对数为纵坐标，得到许多点(lg(eT(t)e(t))，lg(uT(t)u(t)))，经过曲线拟合得到一条曲线。再利用L曲线法选择最佳的r值，其中本文采用最短距离来定位L曲线的最优点。

4 算 例

为了验证上述基于最优输出跟踪的载荷识别方法的正确性和有效性，下面给出3个多源载荷识别的数值算例。在数值算例中，测点的位移响应通过有限元数值仿真计算得到。此外，测点的选择至关重要，该测点的响应要对外载荷具有较强的敏感性，则一般通过敏感性分析来选取合适的测点，且测点的个数要大于等于外载荷的数目，以避免载荷识别时出现不适定性问题。载荷识别前，在仿真计算得到的位移响应中加入一定水平的随机噪声以模拟实验测量的响应，此时带噪声的位移响应可用下式表示

Yerr=Ycal+lnoise·std(Ycal)·rand(-1,1)

(20)

式中Ycal为计算得到的位移响应；std(Ycal)为计算的位移响应的标准差；lnoise为百分数，代表噪声水平；rand(-1,1)为[-1,1]之间的随机数。

4.1 算例 1

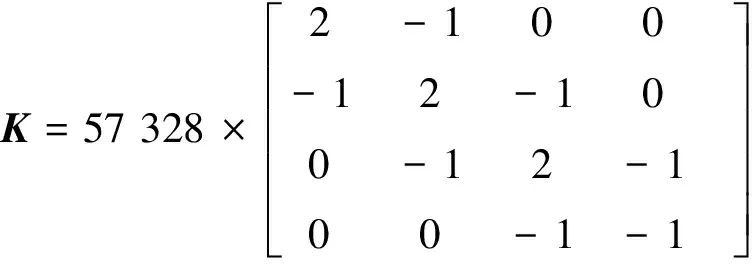
如图1所示一均匀的四层剪切楼板结构[11]，每一层楼板有m=175.126 kg，k=57.328 kN/m，并在第4层楼板和第2层楼板分别施加指数衰减载荷F1和三角形载荷F2的剪切力模拟瞬态冲击载荷，以及在第1层和第3层分别布置测点。

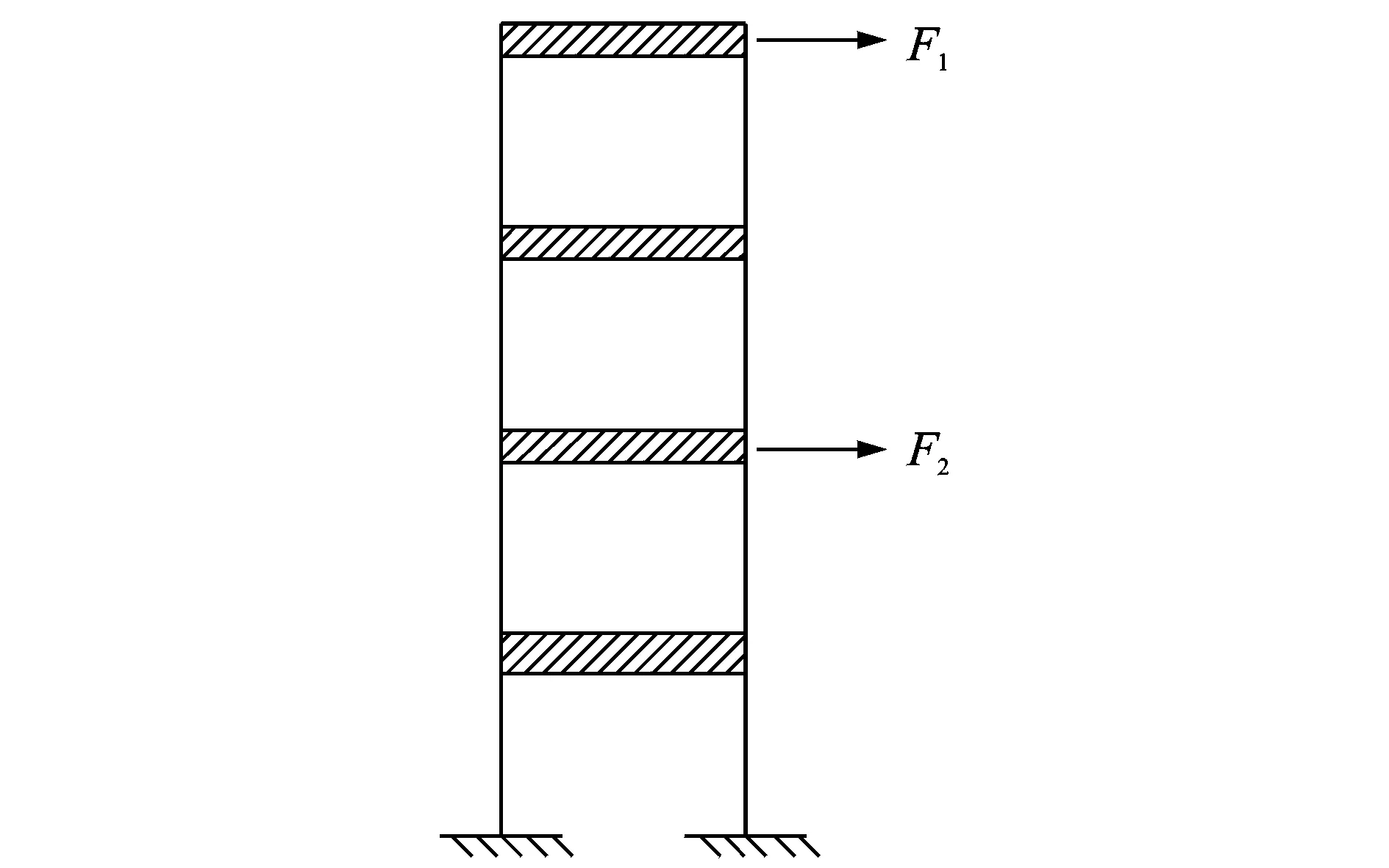
图1 结构简图

按结构动力学的方法可写出结构对应的质量阵和刚度阵：

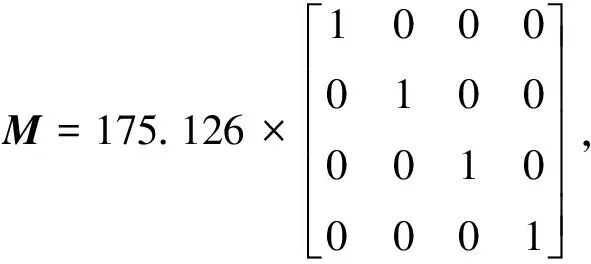
当位移响应中未加入随机噪声时，利用上述载荷识别的方法进行载荷反求重构，其结果如图2所示。从图中可以看出，在测量响应没有噪声污染的情况下，本方法可以很好地实现动态载荷时程的重构。同时，确定最佳r值的L曲线如图3所示。

当在测点位移响应加入5%水平的随机噪声时，利用本文所述方法进行载荷反求重构的结果如图4所示。从图中可以看出，在响应数据受噪声影响的情况下，本方法仍可较好地进行动态载荷识别。图5给出了确定最佳r值的L曲线。

表1给出了当测点位移含有5%水平的随机噪声时，9个不同时间点下识别的载荷值及其相对误差。从表中可以看出，本方法在测量响应受到较低水平噪声影响下识别载荷结果的相对误差均在10%以内。从上述结果可看出，本文所述的载荷识别方法能有效地在时域上重构出施加在结构上的多源载荷。

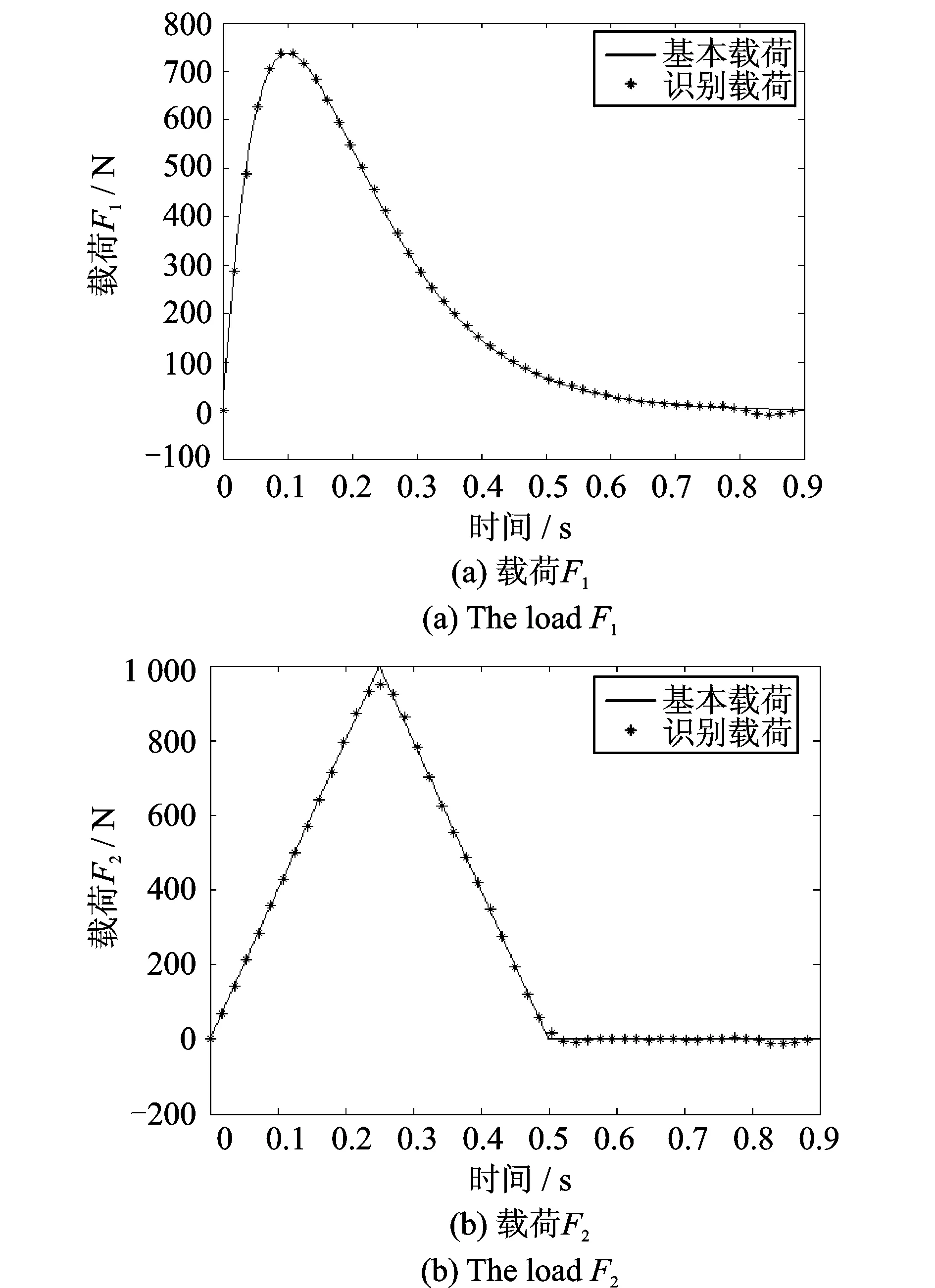
图2 多源载荷识别的结果(零噪声水平)

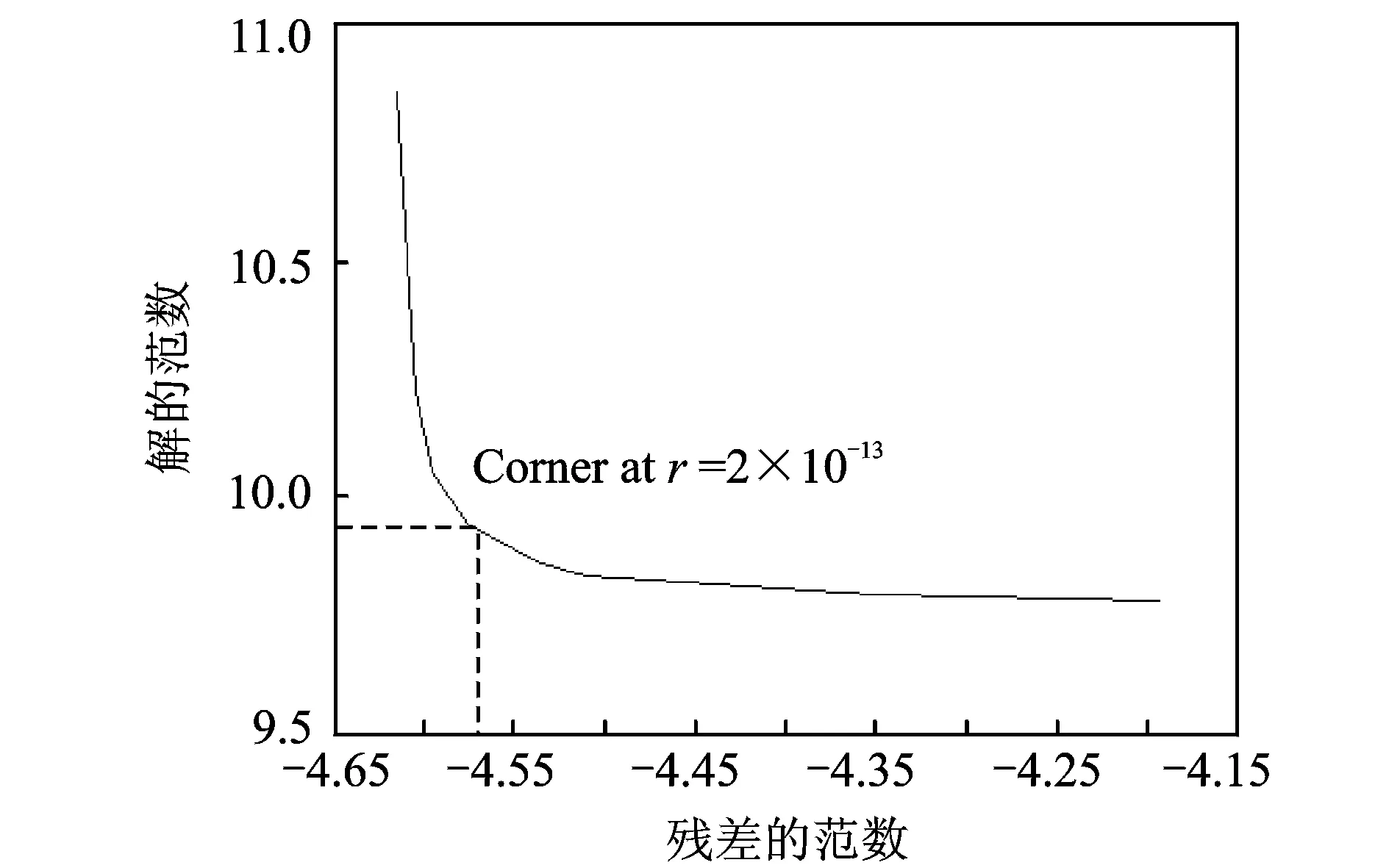
图3 确定最佳r值的L曲线(0%噪声水平)

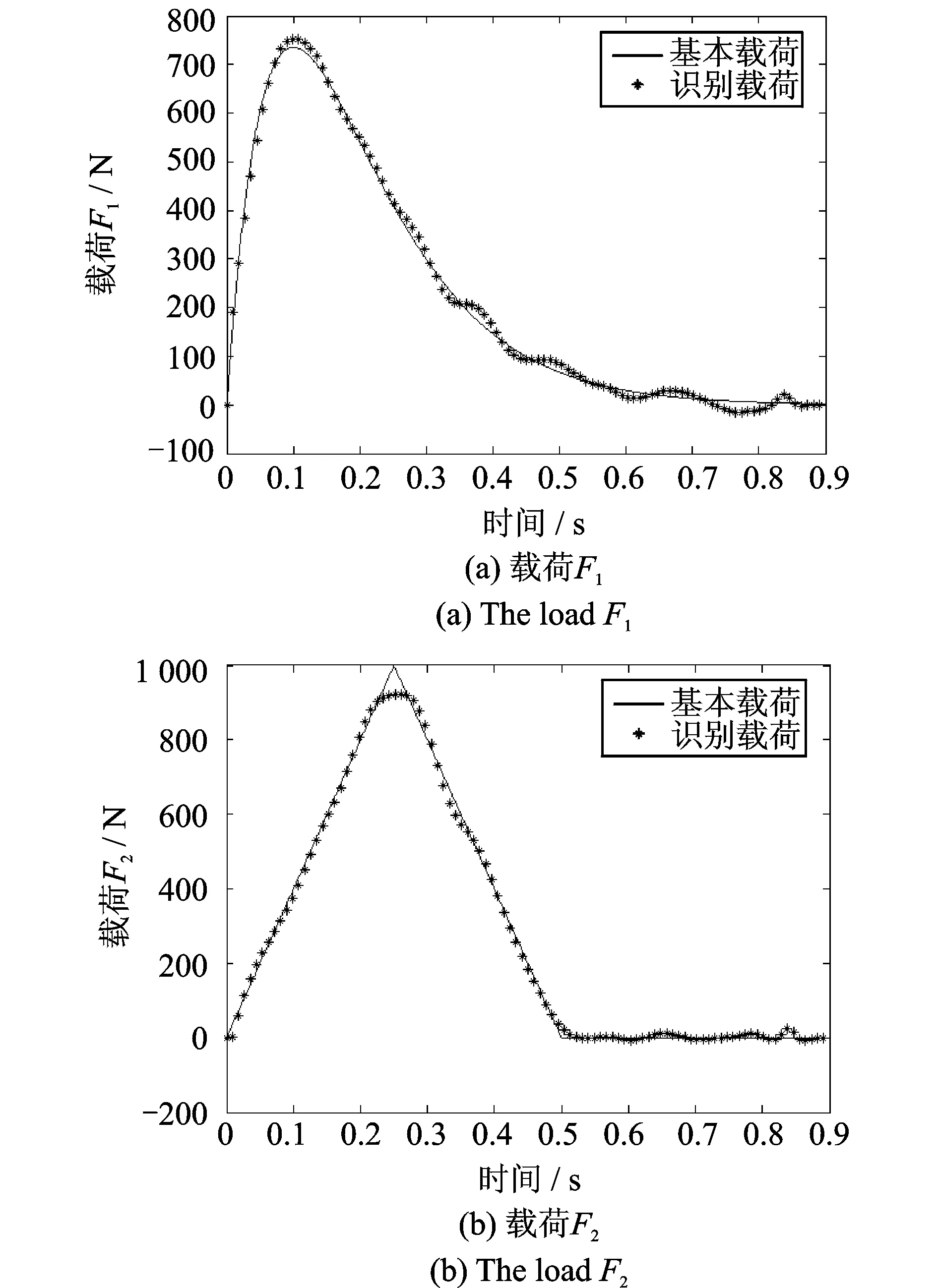
图4 多源载荷识别的结果(5%噪声水平)

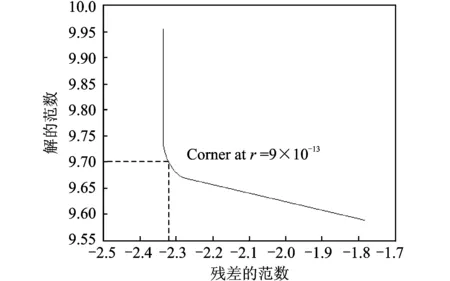
图5 确定最佳r值的L曲线(5%噪声水平)

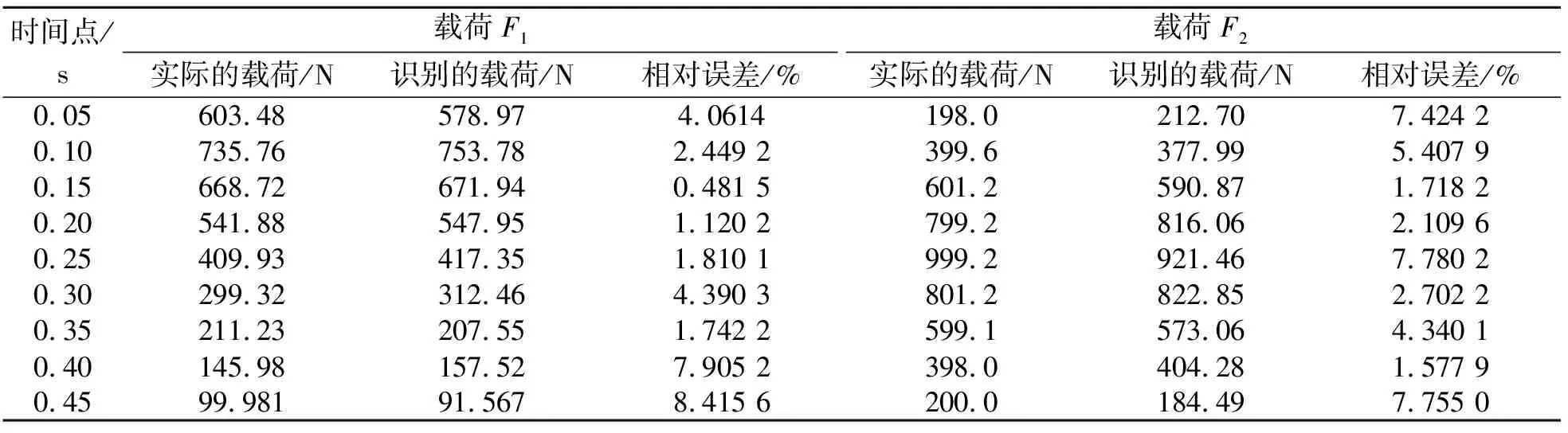
表1 不同时刻识别的动态载荷及其相对误差(5%噪声水平)

4.2 算例2

图6所示为一个高空索道塔架结构有限元模型。该结构立柱下端材料为等边角钢∠200×16，上端为等边角钢∠200×14，横杆、斜杆、撑杆下端为不等边角钢∠160×100×12，上端为不等边角钢∠140×90×10，其他用不等边角钢∠100×80×8，材料特性参数为密度7 860 kg/m3，弹性模量210 GPa，泊松比0.33，阻尼假设为比例阻尼，与质量阵相关的系数为10，与刚度阵相关的系数为2×10-4。整个塔架结构采用梁单元建模，塔架的四个支脚固支。在图6中所示的箭头处分别施变频正弦载荷F1和随机动态载荷F2，这些载荷模拟了高空索道在工作过程中钢索对塔架的垂向作用力。

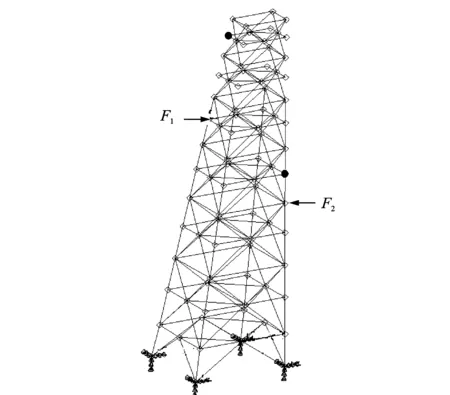
图6 高空索道塔架结构的有限元模型

图6中圆点处标出了响应测量的位置，通过仿真计算，可以得到测点的位移响应，在仿真得到的位移响应中加入10%水平的随机噪声来模拟实验测量的响应。利用本文提出的载荷识别方法进行载荷时间历程重构，其结果如图7所示。从图中可以看出，在测量响应数据受到较高噪声水平影响下，本文方法能够正确有效地实现动态载荷的识别。图8给出了确定最佳r值的L曲线。

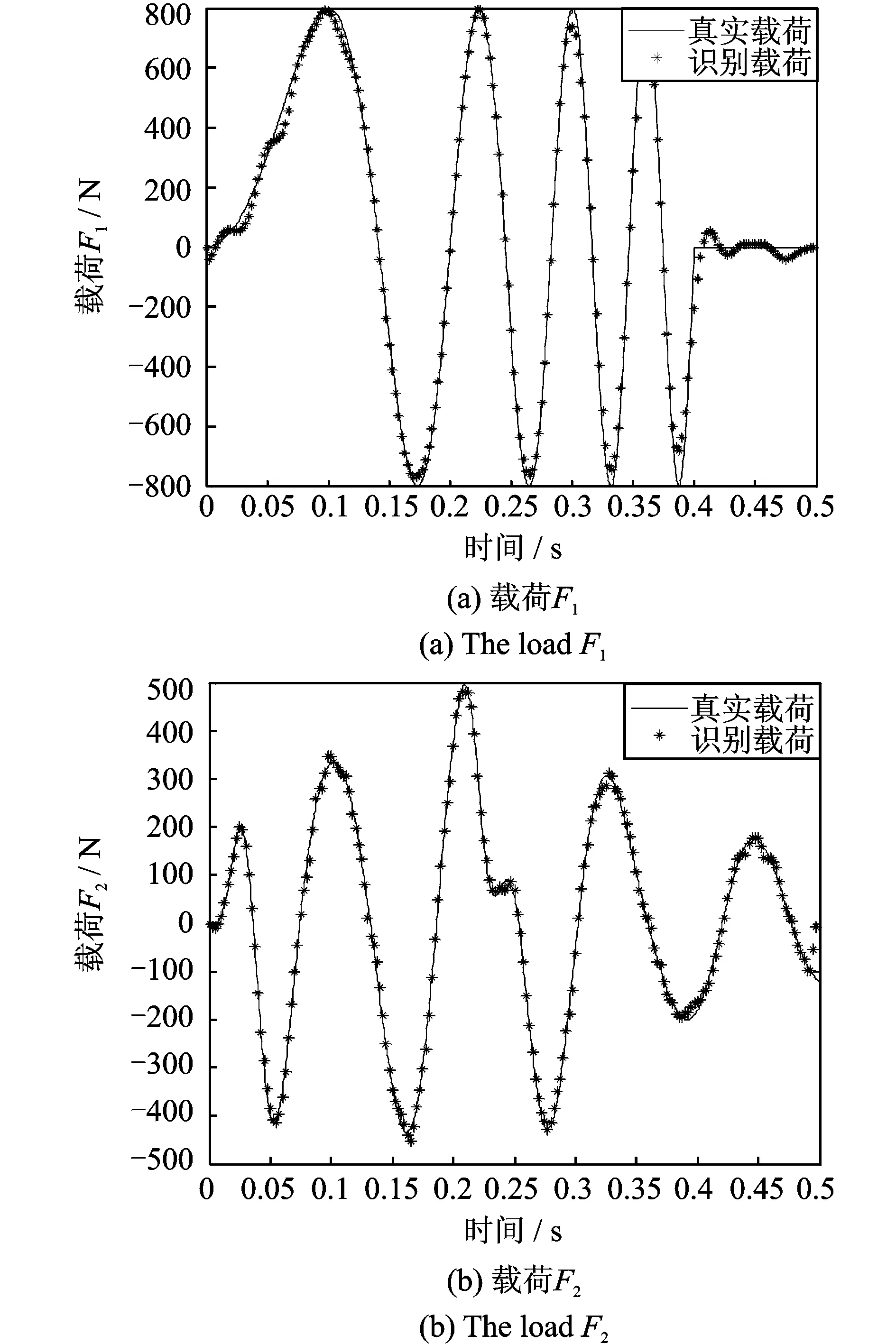
图7 多源载荷识别的结果(10%噪声水平)

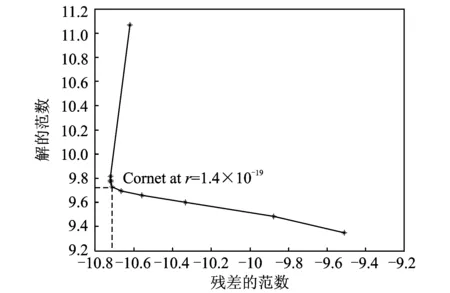
图8 确定最佳r值的L曲线(10%噪声水平)

4.3 算例3

图9所示一个25杆桁架结构，其中杆(1)～(4)有相同的横截面积A1=400 mm2，杆(16)～(25)、杆(11)～(15)和杆(5)～(10)的横截面积分别为A2=500 mm2，A3=600 mm2和A4=800 mm2。横向和纵向杆的长度L=15.24 m，杆的弹性模量为200 GPa，泊松比为0.33，密度为2 800 kg/m3。阻尼假设为比例阻尼，与质量阵相关的系数为0，与刚度阵相关的系数为0.003。连接点12为饺接支座，6，8和10为滚动支座。在3个不同的节点位置分别施加不同时间历程的载荷，其中一种为两个周期的正弦载荷，另外两种分别为一个周期的三角载荷和半个周期的三角载荷，其作用位置分别如图9中箭头F1，F2和F3所示。

建立结构的有限元模型，采用杆单元划分网格，共25个单元和12个节点。选择测点响应为连接点2处的横向位移、连接点3处的纵向位移和连接点7的横向位移。

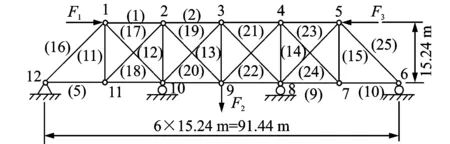
图9 25杆桁架结构

为了测试该算法对噪声的适应能力，在位移响应中加入15%水平的随机噪声作为测量响应，该动态载荷识别的结果如图10所示。从图中可以看出，在测量响应数据受到较高噪声水平影响下，本文载荷识别的方法可以较准确地实现动态载荷时程的重构。图11给出了确定最佳r值的L曲线。

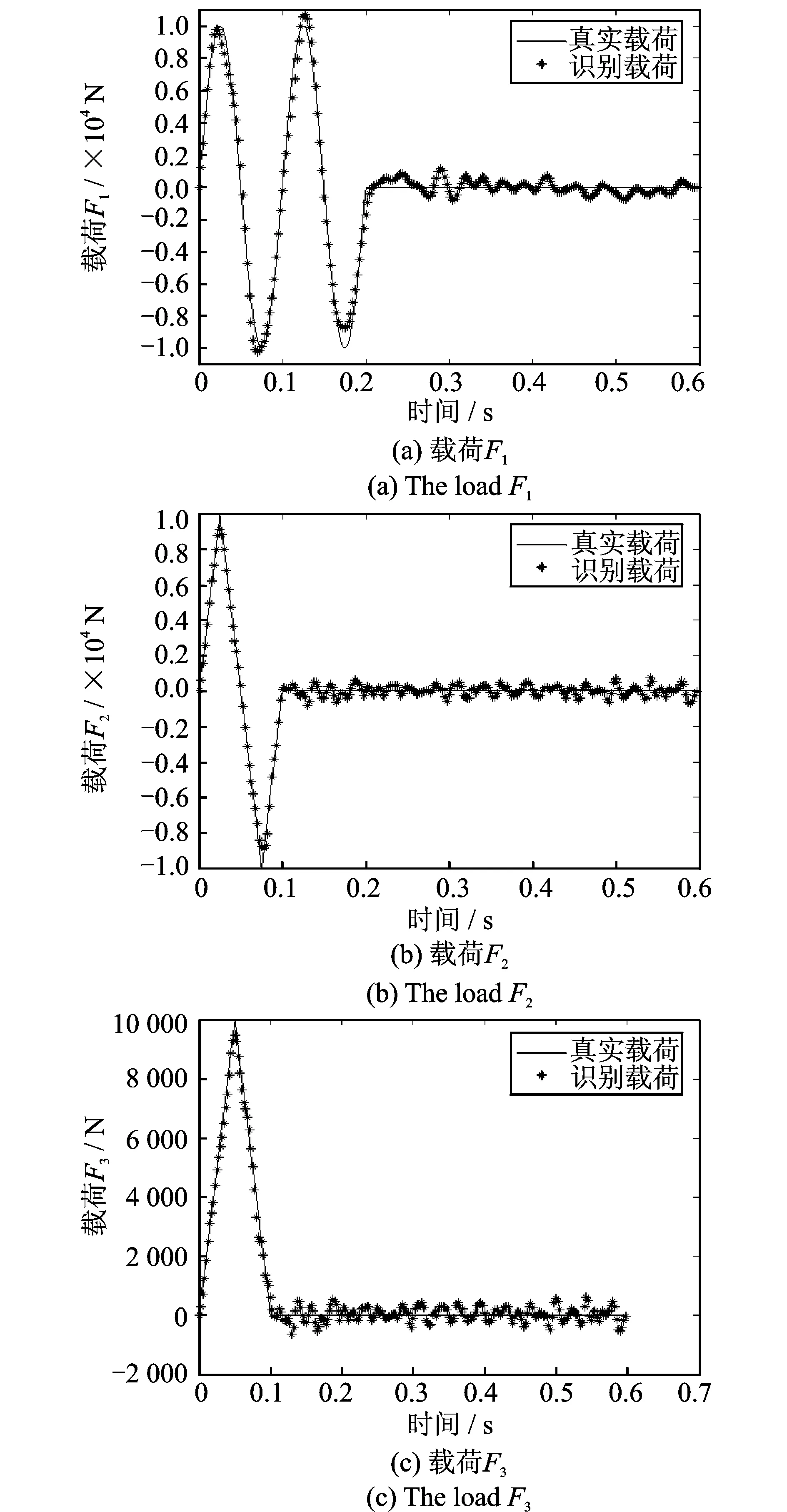
图10 多源载荷识别的结果(15%噪声水平)

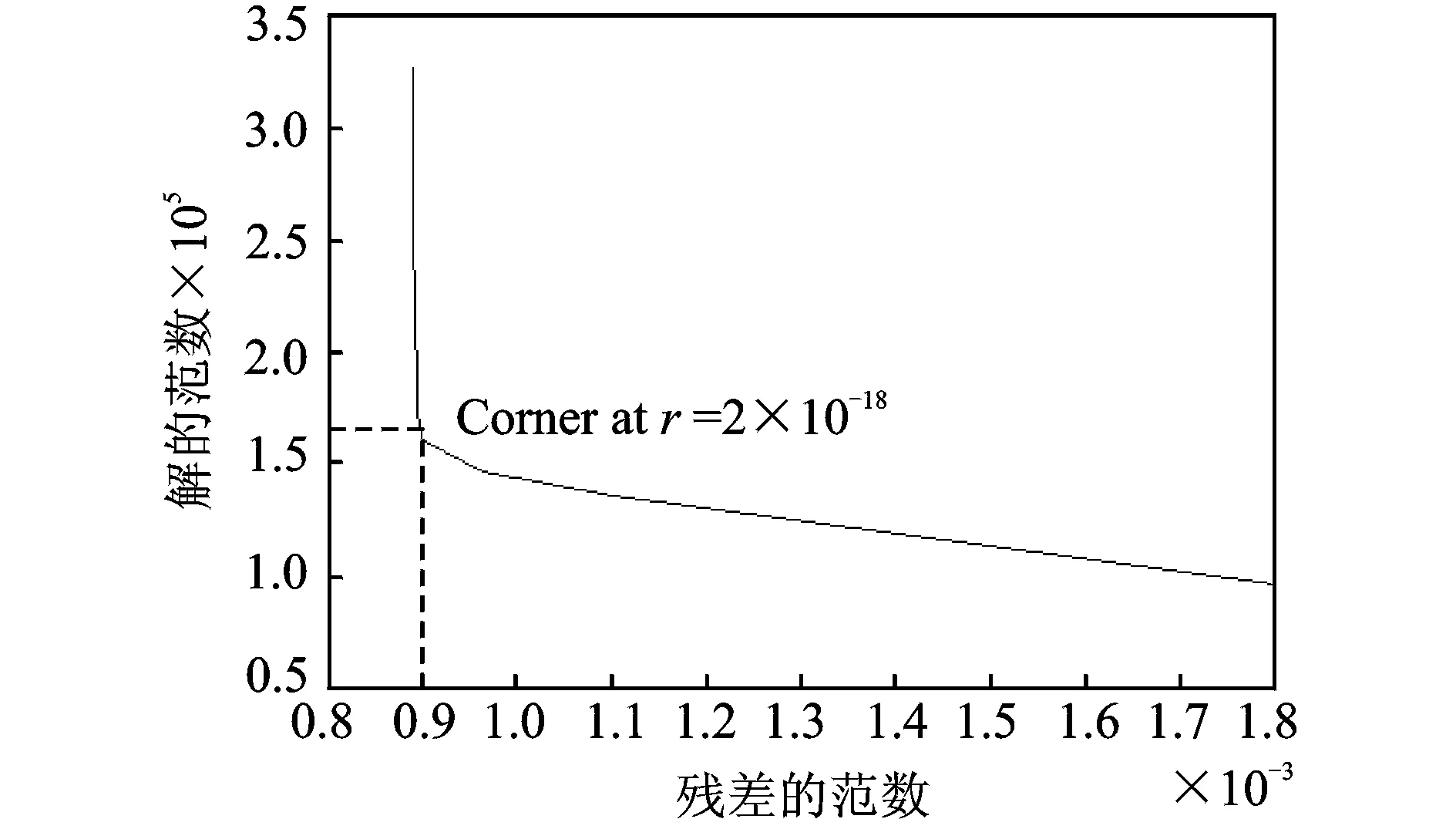
图11 确定最佳r值的L曲线(15%噪声水平)

表2给出了在15%噪声水平下3个不同时刻识别载荷的相对误差。识别载荷的相对误差都在12%以内，这说明本文所述的多源载荷识别方法能有效地抑制噪声对识别结果的影响，具有较好的稳健性。

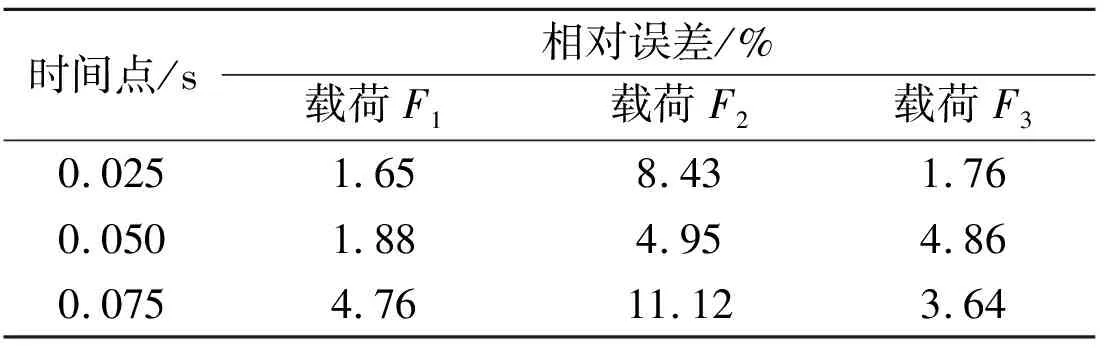
表2 15%噪声水平下不同时刻识别载荷的相对误差

5 结 论

工程实际中动态载荷的识别是一个难度较高且较为复杂的反问题，有许多共性问题需要亟待解决。本文基于最优输出跟踪的思想，提出了一种多源动态载荷识别的方法，并采用L曲线法确定了性能指标中的关键参数。数值算例表明该方法能有效抑制噪声对载荷识别结果的影响，能较为准确、稳健地实现载荷的反演识别。该方法计算简单快捷、抗噪声能力较强，具有一定的工程实际实用价值。

参考文献：

[1] Bartlett F D, Flannelly W D. Modal verification of force determination for measuring vibration loads[J]. Journal of the American Helicopter Society， 1979: 10—18.

[2] Liu Y, Shepard WS. Dynamic force identification based on enhanced least squares and total-squares schemes in the frequency domain[J]. Journal of Sound and Vibration, 2005, 282: 37—60.

[3] 刘杰. 动态载荷识别的计算反求技术研究 [D]. 长沙：湖南大学, 2011.Liu Jie. Research on computational inverse techniques in dynamic load identification [D]. Changsha:Hunan University, 2011.

[4] 韩旭, 刘杰, 李伟杰, 等. 时域内多源动态载荷的一种计算反求技术 [J]. 力学学报, 2009, 41(4): 598—605.Han Xu, Liu Jie, Li Weijie, et al. A computational inverse technique for reconstruction of multisource loads in time domain [J]. Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(4): 598—605.

[5] 伍乾坤, 韩旭, 刘杰, 等. 一种直接求解的动态载荷识别方法[J]. 应用力学学报, 2011, 28(2): 201—205.Wu Qiankun, Han Xu, Liu Jie, et al. A dynamic load identification method based on direct solution [J]. Chinese Journal of Applied Mechanics, 2011, 28(2): 201—205.

[6] 章继峰, 张博明, 杜善义. 最优化方法在动态载荷时程重构中的应用研究[J]. 振动与冲击, 2006, 25(4): 5—8.Zhang Jifeng, Zhang Boming, Du Shanyi. Application of optimization method to kinetic loading time history reconstruction [J]. Journal of Vibration and Shock, 2006, 25(4): 5—8.

[7] Paultre P. Dynamics of Structures [M]. Wiley-ISTE, 2010.

[8] Anderson B D O, Moore J B. Linear Optimal Control[M]. Prentice-Hall Inc, 1971.

[9] 李荣华, 刘播. 微分方程数值解法[M]. 北京: 高等教育出版社, 2009.Li Ronghua, Liu Bo. Numerical Solution of Differential Equations [M]. Beijing: Higher Education Press, 2009.

[10] Hansen P C, Leary D P. The use of the L-curve in the regularization of discrete ill-posed problems [J]. SIAM Journal on Scientific and Statistical Computing, 1993, 14:1 487—1 503.

[11] 帕兹 M. (美)著．结构动力学——理论与计算[M]. 李裕澈, 刘勇生，译. 北京: 地震出版社, 1993.Paz M. Structural Dynamics-Theory and Computation [M]. Beijing: Publish House of Seismological Bureau, 1993.