气囊着陆缓冲系统冲击动力学模型修正方法

何 欢， 倪 磊, 何 成, 陈国平

(1.南京航空航天大学振动工程研究所， 江苏 南京 210016；2.机械结构力学及控制国家重点实验室， 江苏 南京 210016；3.中航通用飞机有限责任公司， 广东 珠海 519040)

引 言

为节约研制经费，缩短研究周期，可以采用仿真分析手段对气囊着陆缓冲系统的着陆缓冲性能进行模拟。准确可靠的气囊着陆缓冲系统冲击动力学模型是开展仿真分析的前提条件。模型修正技术是获得准确可靠的气囊着陆缓冲系统冲击动力学模型的一种行之有效的方法。

近30年来，模型修正技术在结构动力学领域得到深入发展，国内外研究工作者针对结构动力学各个领域提出了多种有限元模型修正的方法[1～3]，其中以基于模态参数型修正方法发展相对较早，应用最为广泛。目前基于灵敏度的模型修正已有成熟的解析公式和有效算法[4]。Dascotte对修正方程的性态问题进行了研究[5]。Friswell等人提出了一种基于子空间的修正参数选择方法，还对修正方程求解进行了讨论[6,7]。此外，Friswell还讨论了阻尼的不同处理方法对模型的影响[8]。Khodaparast等人采用非概率型描述方式对考虑不确定性的模型修正问题进行了探讨[9,10]。

相对而言，考虑非线性因素的模型修正问题研究起步较晚，于上世纪90年代才逐渐开展开来。Francois等人以多自由度系统为对象，比较了在瞬态时域响应下基于最小二乘法和主分量分解两种修正方法[11]。John等人通过特征抽取压缩数据规模，采用代理模型技术完成了带不确定性冲击问题的模型修正[12]。Hasselman等人基于主分量分解技术对非线性模型相关性、修正以及不确定性量化进行了研究，并通过数值算例进行了验证[13]。费庆国等通过神经网络方法对考虑非线性因素的梁结构进行了模型修正[14]。

作为非线性动力学模型修正问题中的一类，冲击动力学模型修正问题具有较强挑战性。由于试验触发、采样频率等方面的原因，试验实测冲击响应信号与计算冲击响应信号往往不同步，给冲击动力学模型修正带来了很大困扰。郭勤涛等以冲击响应谱为响应特征，采用子结构模型修正方法对车架结构冲击响应进行研究，但采用的冲击动力学模型仍然是传统的线性模型[14]。除此之外，冲击动力学模型修正方面的研究鲜有报导。

本文探索一种适用于气囊着陆缓冲系统冲击动力学模型修正方法。考虑到气囊模型和回收舱模型的相互独立性，采用分级修正思路，在修正后的回收舱结构动力学模型基础上，结合冲击过载主要特点，定义冲击响应关键点和冲击过载序列。然后，以关键点冲击过载序列实测结果与计算结果之间的误差范数为修正目标，利用增广径向基函数法构造修正目标关于修正变量的代理模型。最后，通过对代理模型寻优获得修正结果。

1 径向基函数法

径向基函数法(RBF)是一种用于多元离散数据的插值方法，其基本思想是由一系列对称的、以样本点为中心的基函数的线性组合来逼近真实模型，是目前较为通用的一类构造全局近似函数的方法。

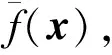
(1)

式中n为样本点数，x为修正变量构成的向量，xi为第i个样本点，φ(·)为基函数，λi为待定加权系数。

定义

r=‖x-xi‖

(2)

式中 ‖·‖为欧式范数，‖x-xi‖表征了任意修正变量与第i个样本点之间的欧拉距离。

将n个样本点的函数值代入式(1)，得

(3)

将式(3)表示为矩阵形式，得

f=Aλ

(4)

式中

(5)

将经典RSM和RBF相结合，可以得到下式所示的增广径向基函数模型

(6)

式中m为RSM模型阶数，qj(·)为第j阶多项式，βj(j=1,2，…，m)为待定加权系数。

引入正交性条件

(7)

将式(7)代入式(6)，结合式(5)，并将方程改写成矩阵形式，得

(8)

式中Qij=qj(xi)，β={β1β2…βm}T。

2 冲击响应置信因子

考虑到冲击响应的特征主要是冲击响应幅值和脉冲宽度，本文引入冲击响应峰值点及峰值点两侧的关键时刻点，通过比较关键点处的试验结果和计算结果来评价计算结果与试验结果之间的吻合程度。

设实测冲击过载为a，记实测冲击过载峰值点时刻为tp，以等时间间隔Δt从实测冲击过载序列中提取出过载峰值点及峰值点两侧共2n+1个时刻的冲击响应过载，构成实测关键点冲击过载序列

(9)

式中ai=a(tp+iΔt)，i=-n,-n+1,…，n。

(10)

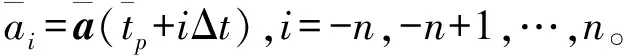
从式(9)和(10)不难看出，关键点冲击过载序列实际上描述出了冲击响应峰值点附近区域的冲击响应曲线基本特征。

定义冲击响应置信因子

(11)

从式(11)可以看出，RAC值越接近1.0，表示计算结果和试验结果的吻合程度越高，就说明冲击动力学模型越精确。

3 冲击响应模型修正

3.1 修正目标

记实测过载与计算过载之间的误差为

ε=at-ac(x)

(12)

定义误差范数

f(x)=εTε

(13)

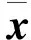
(14)

由于气囊着陆缓冲动力学模型较为复杂，着陆缓冲动力学分析也涉及到接触不等式约束、大变形等非线性因素，无法直接建立模型参数x与系统冲击响应之间的显式函数关系。也就是说，无法通过模型参数x直接获得式(13)所示的误差范数f(x)的显式函数表达式。

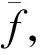
(15)

3.2 修正流程

根据上述讨论，可以给出如下模型修正基本流程：

1．采集冲击响应试验数据；

2．寻找冲击响应峰值点，选择适当的时间间隔，在冲击响应峰值点两侧选定若干过载数据，构造实测关键点冲击过载序列at；

3．构造修正变量样本空间x1,x2,…,xr，对任意样本点xj，建立气囊着陆缓冲系统动力学模型，并计算冲击过载，构造计算关键点冲击过载序列ac(xj)；

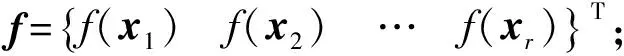
5．选择基函数，根据式(8)，确定λ和β；

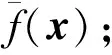
7．对代理模型进行优化，给出修正分析结果。

4 气囊系统冲击动力学模型修正算例

4.1 试验模型

气囊着陆缓冲系统试验件由3个相互连通的底部气囊和上部回收支架构成，如图1所示。

图1 气囊着陆缓冲系统试验件

回收支架总质量为3.0 kg，底部为3个圆形钢板，与气囊之间通过接触关系发生作用，顶部为等边三角形的钢板，有若干对称分布的螺孔，用于安装配重和加速度传感器。

气囊着陆缓冲系统冲击动力学试验方案示意图如图2所示。在开展试验时，通过行车和卷扬机将气囊系统试验件吊到预定高度和位置后，控制炸弹钩开启，完成气囊着陆系统的自由投放。

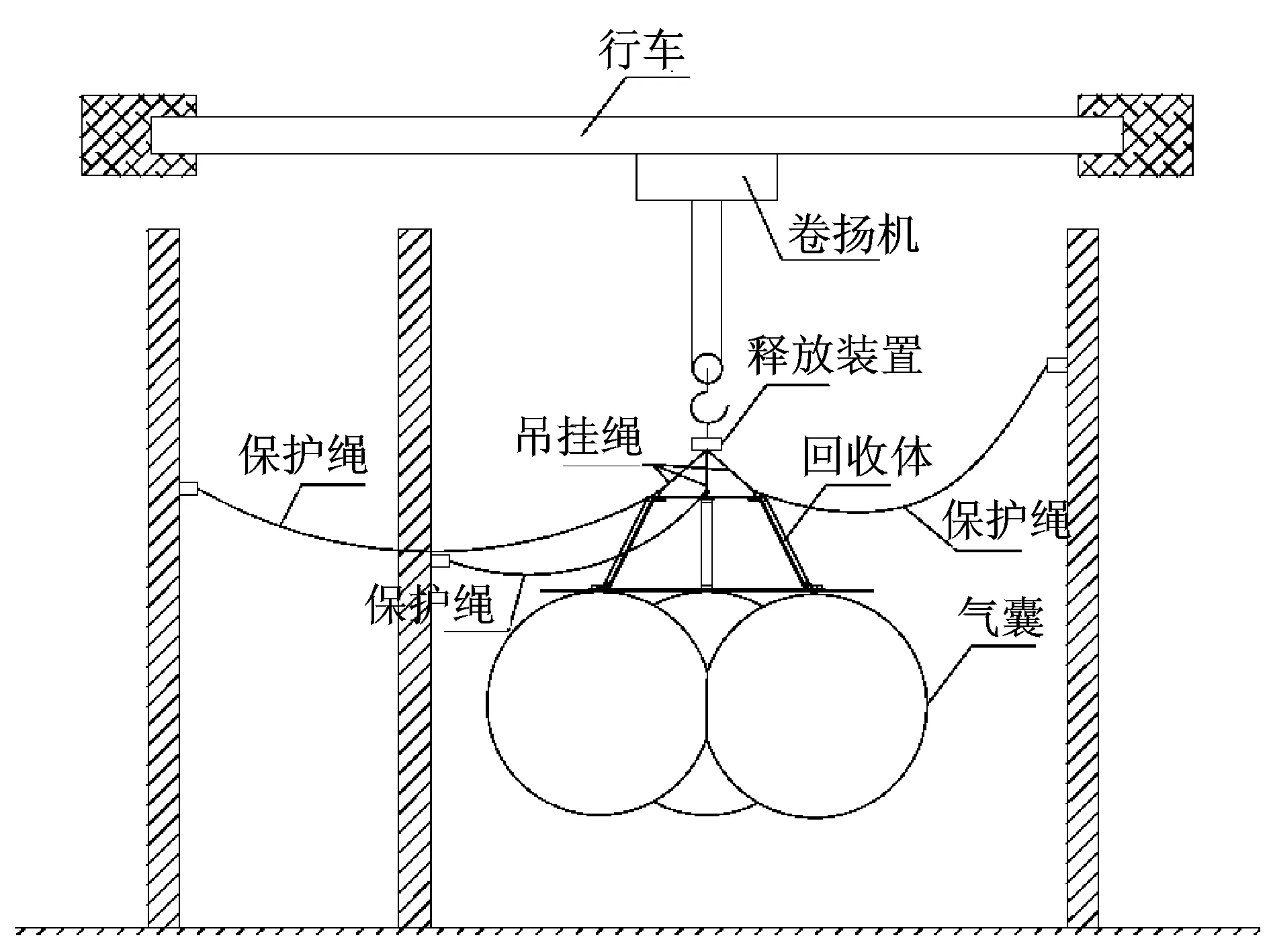
图2 气囊着陆缓冲系统冲击动力学试验方案示意图

采用BW14108加速度传感器测量回收支架上的着陆过载，选用动态信号分析仪Agilent35670采集、记录加速度信号。

4.2 仿真分析模型

根据试验样件建立了气囊着陆缓冲系统冲击动力学试验仿真分析模型，回收支架采用壳单元模拟，气囊织物采用膜单元模拟，气囊外部收缩绳采用索单元模拟，气囊内部气体采用均匀压力模型模拟，由理想气体方程描述

PV=nRT

(16)

式中P为囊内压强，V为气囊体积，n为气体摩尔数，R为气体常数，T为囊内气体温度。

外界环境气压为1个标准大气压，即101 325 Pa。气囊模型与回收支架模型底部之间通过接触关系模拟。所建立的气囊着陆缓冲系统有限元模型如图3所示。

图3 气囊着陆缓冲系统有限元模型

气囊系统和回收支架的动力学性能特征对缓冲过载均有影响。考虑到气囊和回收支架模型的相互独立性，对回收支架和气囊系统分别进行模型修正。

4.3 回收支架的结构动力学模型修正

通过模态试验对回收支架结构动力学模型进行修正。在试验中，将3个底部圆盘固定，采用锤击法测得40个点处的频响函数曲线，通过I-DEAS识别出固有频率及对应的振型。

由于回收支架各部件之间通过螺栓连接，考虑到螺栓连接对系统动特性有显著影响，本文在建立回收支架结构动力学模型时采用6自由度弹簧单元来等效模拟螺栓连接。

经初步试算可以发现，用于模拟螺栓连接的6自由度弹簧单元的转动刚度在一定范围内对模态分析结果不敏感。为减少修正变量，给定螺栓转动刚度，选择螺栓3个平动刚度、板厚、材料弹性模量和密度作为修正变量。修正变量参数设计空间如表1所示。

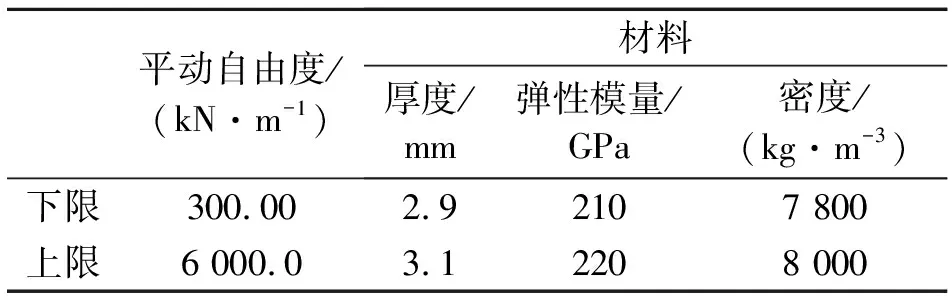
表1 回收支架修正变量参数设计空间

采用MSC.Nastran模态分析模块计算回收支架固有频率，以回收支架实测固有频率与计算结果中对应的固有频率的残差的最小二范数为修正目标，以增广径向基函数法构造修正变量关于修正目标函数的全局近似模型，并通过遗传算法进行寻优分析。修正结果如表2所示。

表2 回收支架修正结果

表3给出了根据修正结果计算得到的回收支架前4阶固有频率与模态试验实测固有频率的对比。

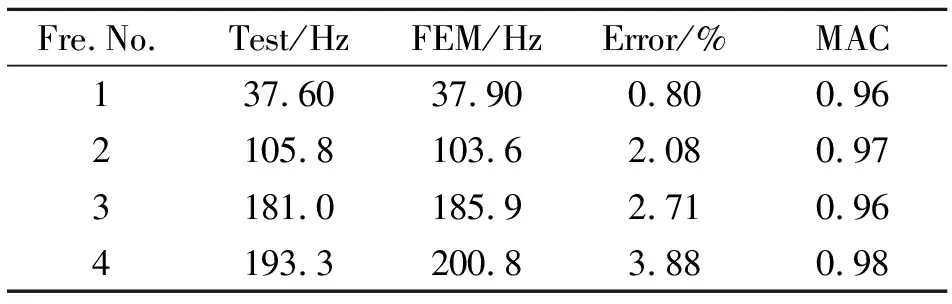
表3 试验实测固有频率与有限元计算结果对比

从表3中可以看出，修正后的回收支架有限元模型计算结果与试验实测结果吻合程度很好。为了检验修正后的模型预报能力，开展了回收支架自由-自由模态试验，试验实测前7阶固有频率与计算得到的固有频率对比如表4所示。

从表4中可以看出，回收支架自由-自由模态试验实测前7阶固有频率与修正后模型计算得到的固有频率误差均小于5%，满足工程精度要求，说明模型修正结果可靠，可以将该模型用于后续着陆缓冲动力学模型中。

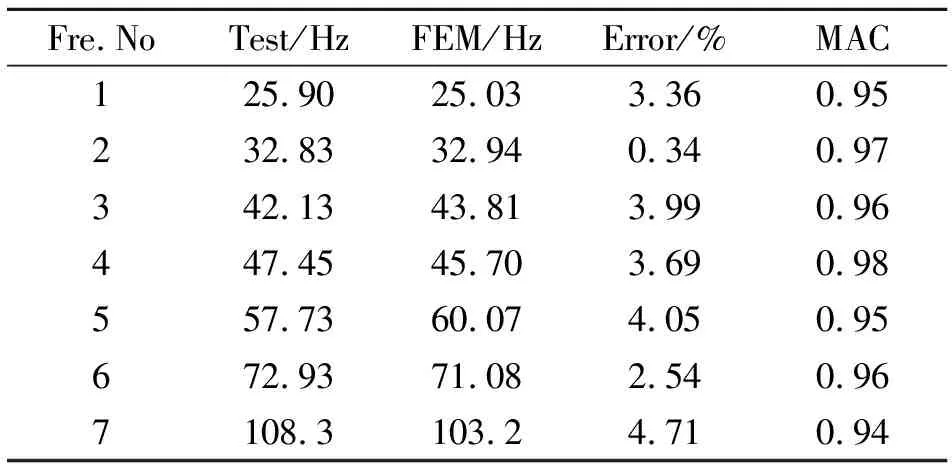
表4 试验实测固有频率与有限元计算结果对比(自由-自由)

4.4 气囊系统的模型修正

以图2所示的试验方案进行气囊着陆缓冲系统冲击动力学试验，将气囊系统起吊至与地面1.0 m高度，通过自由释放方式投放，气囊与地面接触速度为4.43 m/s，系统总质量为5.9 kg。

对气囊着陆缓冲系统来说，气囊内压和气囊织物弹性模量对冲击响应的影响显著，而且这两个参数不易准确测定。为此，本文选择气囊内压和气囊织物等效弹性模量作为修正变量，设计空间如表5所示。

表5 气囊模型修正变量参数设计空间

试验设计取为2因子，7水平的全面析因试验设计，共49个样本点。

对每一个样本点，采用MSC.Dytran计算气囊着陆缓冲系统的冲击过载，在冲击过载曲线的峰值点两侧每间隔1 ms取一个关键点，包括冲击过载峰值点在内，构造出一共包括33个关键点的冲击过载序列，并计算误差范数。

在计算完全部样本点后，利用增广径向基函数法构造误差范数的代理模型，如图4所示。

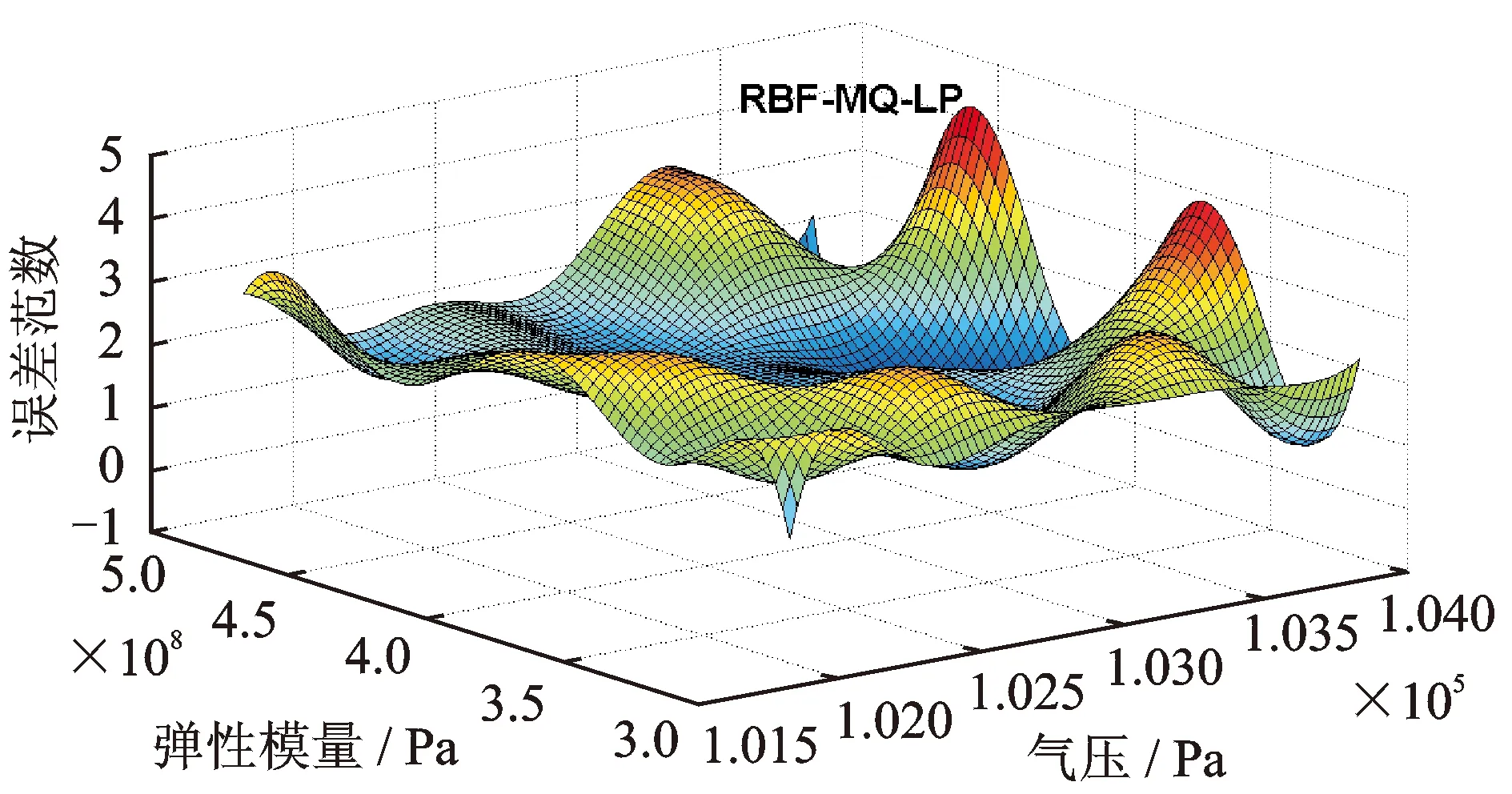
图4 误差范数的代理模型曲面

对代理模型进行寻优分析，得到参数修正结果如表6所示。

表6 气囊模型修正结果

根据修正结果对气囊着陆缓冲系统试验冲击过程进行模拟，得到的计算结果与试验实测最大冲击过载的比较如表7所示。

表7 修正后模型计算过载峰值与试验值的对比

计算得到的冲击过载时间历程与试验实测冲击过载时间历程的对比如图5所示。冲击响应置信因子RAC=0.998 5。

图5 修正后模型计算过载与试验过载曲线对比

从表7中容易看出，修正后的模型计算得到的冲击过载峰值与试验实测过载峰值之间误差仅有0.37%。图5所示的计算冲击过载曲线与试验实测冲击过载曲线吻合程度也很好，冲击响应置信因子接近1.0。说明本文提出的气囊着陆缓冲系统冲击动力学模型修正方法具有良好的修正精度。

为检验修正后的气囊缓冲系统冲击动力学模型预报精度，在气囊顶部回收支架上增加1.0 kg配重，系统总质量为6.9 kg，气囊与地面接触速度仍然为4.43 m/s。

利用修正后的气囊着陆缓冲系统冲击动力学模型对这种试验状态进行仿真模拟，得到的计算结果与试验实测最大冲击过载的比较如表8所示。

表8 修正模型计算过载峰值与试验值的对比

从表8中容易看出，利用修正模型对新试验状态下的着陆冲击过程进行模拟，计算过载峰值与试验实测过载峰值之间误差为1.55%。

计算冲击过载与试验实测过载曲线的对比如图6所示。从图中可以看出，计算冲击过载曲线与试验实测冲击过载曲线也基本吻合，冲击响应置信因子RAC=0.990 8，仍然接近1.0，说明修正模型预报精度良好，可以满足工程精度要求。

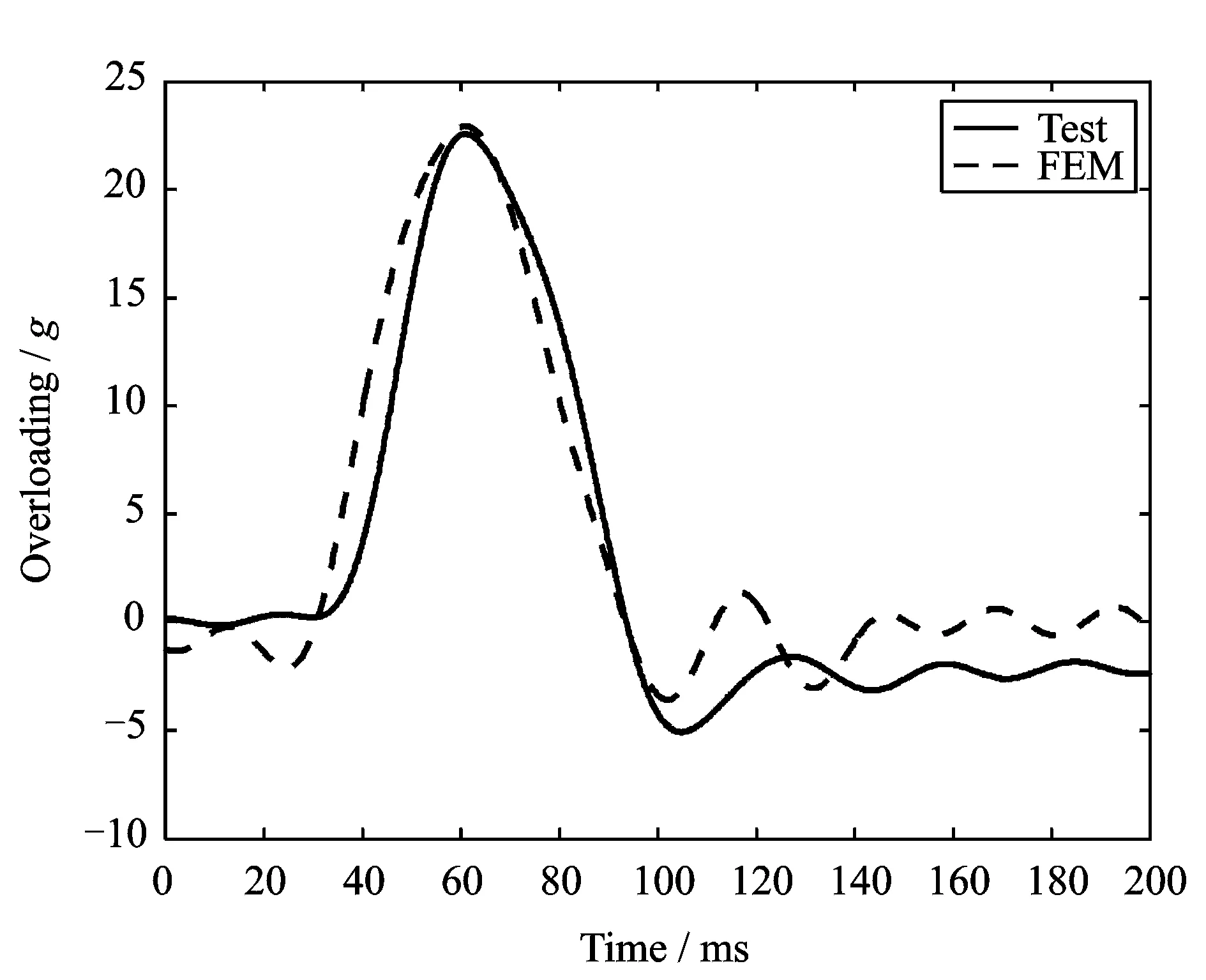
图6 修正模型计算过载与试验过载曲线对比

5 结 论

本文研究结果表明，采用分级修正思路，结合RBF方法构造冲击响应计算结果与试验结果之间的残差的代理模型，并通过常规优化算法来实现气囊着陆缓冲系统冲击动力学模型修正是可行的。数值算例表明，采用本文方法可以获得具有高计算精度的气囊着陆缓冲系统冲击动力学模型。

研究结果还表明，在构造冲击响应计算结果与试验结果的残差时，选择峰值点及两侧的关键点处的冲击响应数据可以有效解决因采样频率和试验触发差异带来的计算结果与实验结果数据比较与分析方面的困难。

虽然本文研究对象是气囊着陆缓冲系统，但所提出的研究方法具有一般性，也可以推广到一般的冲击动力学模型修正问题中。

参考文献：

[1] Chen J C, Garba J A. Analytical model improvement using modal test results[J]. Journal of AIAA, 1980,18(6):684—690.

[2] Link M. Identification and correction of errors in analytical models using test data: theoretical and practical bounds[A]. Proceedings of the 8th International Modal Analysis Conference[C]． Orlando, Kissimmee, 1990:570—578.

[3] Lin Xiankun, Zhang Lingmi， Guo Qintao, et al. Dynamic finite element model updating of prestressed concrete continuous box-girder bridge[J]. Earthquake Engineering and Engineering vibration, 2009,8(3):399—407.

[4] 秦仙蓉.基于灵敏度分析的结构计算模型修正技术及相关问题研究[D].南京:南京航空航天大学,2001.QIN Xianrong. A study of sensitivity analysis based computational model updating of dynamic structures and the relevant issues[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2001.

[5] Dascotte E, Strobbe J, Hua H. Sensitivity-based model updating using multiple types of simultaneous state variables[A]. Proceedings of the 13th IMAC[C]. Nashville, USA, 1995:1 113—1 116.

[6] Friswell M I, Mottershead J E, Ahmadian H. Combining subset selection and parameter constraints in model updating[J]. Journal of Vibration and Acoustics, 1998,120(4):854—859.

[7] Mottershead J E, Mares C, Friswell M I. Selection and updating of parameters for an Aluminum space-frame model[J]. Mechanical System and Signal Processing, 2000,14(6):923—944.

[8] Prells U, Friswell M I. A measure of non-proportional damping[J]. Mechanical System and Signal Processing, 2000,14(2):125—137.

[9] Khodaparast H H, Mottershead J E, Badcock K J. Propagation of structural uncertainty to linear aeroelastic stability[J]. Computers and Structures, 2010,88(3/4):223—236.

[10] Marques S, Badcock K J, Khodaparast H H, et al. Transonic aeroelastic stability predictions under the influence of structural variability[J]. Journal of Aircraft, 2010,47(4):1 229—1 239.

[11] Hemez F M, Doebling S W. Test-analysis correlation and finite element model updating for nonlinear transient dynamics[A]. Proceedings of the 19th International Modal Analysis Conference[C]. Kissimmee, FL, USA, 1999:1 501—1 510.

[12] John F Schultze, Francois M Hemez, Scott W Doebling, et al. Statistical based non-linear model updating using feature extraction[A]. Proceedings of IMAC-XIX, the 19th International Modal Analysis Conference[C]. Kissimmee, Florida, 2001:18—26.

[13] Hasselman T K, Anderson M C, Wenshui G. Principal components analysis for nonlinear model, correlation, updating and uncertainty evaluation[A]. Proceedings of the 16th IMAC[C]． Santa Barbara, CA, 1998:664—651.

[14] 费庆国,李爱群,张令弥.基于神经网络的非线性结构有限元模型修正研究[J].宇航学报,2005,26(3):267—269.FEI Qingguo, LI Aiqun, ZHANG Lingmi. Study on finite element model updating of nonlinear structures using neural network [J]. Journal of Astronautics, 2005,26(3):267—269.

[15] 郭勤涛,张令弥.以冲击响应谱为响应特征的有限元模型确认[J].振动与冲击,2005,24(6):32—36.Guo Qintao, Zhang Lingmi. FE model validation using shock response spectrum as response feature[J]. Journal of Vibration and Shock, 2005,24(6):32—36.