基于概率密度空间划分的符号化时间序列分析及其在异常诊断中的应用
胡世杰, 钱宇宁, 严如强
(东南大学仪器科学与工程学院,江苏 南京 210096)
引 言
在机械系统中异常检测是指在给定的数据集中提取出特征,并利用提取出的特征来判断其状态是正常还是异常。随着科学技术和现代工业的飞速发展,国民经济的机械、能源、石化、运载和国防等行业的机械设备日趋大型化、高速化、集成化和自动化,这对中国经济高速发展提供了有力保障。但是由于机械设备的故障失效引起的灾难性事故屡有发生,若能准确及时识别机械系统运行当中异常状态,对机械系统的安全运行,避免重大和灾难性事故意义重大[1]。随着对高质量、低能耗以及安全生产的需求,已经有多种信号处理方法引入到机械系统的异常检测当中。其中,符号化时间序列分析由于具有计算效率高,高信噪比等特性被广泛地应用在异常诊断当中。
符号化时间序列分析STSA起源于上世纪90年代中期,它是由符号动力学理论、混沌时间序列分析和信息论发展起来的一种新的信息分析方法。在符号化时间序列分析当中,最关键的一步是对原始时间序列的符号化。符号化即是对原始时间序列进行离散化,将有多种不同值的数据序列变为仅有几个互不相同符号的序列。这一过程能够保留原始时间序列当中的大尺度特征,从而降低动力学噪声和测量噪声的影响[2];同时由于数据的符号化,其计算效率大大提高。目前,符号化方法可以分为两类:1)基于值域的符号化方法;2)基于分布的符号化方法。基于值域的符号化方法主要是通过对时间序列值域的分析来进行符号化。例如,Asoky Ray提出了统一划分符号化的方法[3],该方法首先确定时间序列的最小值与最大值,然后将值域划分为N个值域大小相同并且连续的区间。其中N为采用符号的个数。Rajagopalan在统一划分符号化方法的基础上提出了最大信息熵符号化方法[4],该方法在符号化过程当中使每个符号出现的概率相同,从而保证在使用相同符号来符号化原始时间序列时系统拥有最大的信息熵。该方法可以通过以下步骤实现:首先将原始时间序列按照从小到大的顺序排列,然后将整个序列划分为N段长度相同的区间,最后将每个区间对应到一个符号即完成了符号化。这些基于值域的符号化方法(例如,等区间的统一划分,等概率的最大信息熵划分)在大多数情况下是有效的,但是机械系统的运行状态与时间序列概率分布是密切相关的,符号化过程当中不考虑其分布将会导致符号化后的信息丢失。另一类是基于分布的符号化方法,这类方法基于时间序列符合高斯分布假设。例如,Lin假设时间序列符合高斯分布(N(0,1)),然后根据高斯分布确定“断点”以得到若干等概率的区域[5]。然而实际应用中时间序列可能形成于一种未知的动力系统或者伴随着不同水平的噪声,这将导致时间序列实际分布与高斯分布相差甚远。所以基于分布的符号化方法有一定的局限性,不是一种普遍适用的方法。受上述研究的启发,本文提出一种称为概率密度空间划分的符号化方法。概率密度符号化方法结合了基于值域的符号化方法与基于分布的符号化方法的优点。该方法首先对原始时间序列进行统计分析并计算其概率密度图,然后选择时间序列的平均值作为概率密度图的中心点,以中心点为对称中心时间序列将被划分为等概率的若干区域,之后将每个区域映射到一个符号。通过上述步骤,可以得到基于概率密度符号化方法的符号序列。为了对符号序列进行异常检测,最后对符号化时间序列进行编码。本文第二部分将介绍符号化时间序列分析的理论背景以及概率密度符号化方法的实现;第三部分通过实际轴承疲劳实验数据验证算法并与其他划分方法的检测效果进行比较,最后一部分得出结论。
1 符号化时间序列分析与概率密度符号化方法
时间序列的符号化分析分为两步[6,7]:先将时间序列转化为符号序列,再对符号序列进行统计分析。
为了详细介绍算法流程,先定义以下变量:xn={x(1),x(2),…,x(n)}表示直接从传感器获得的时间序列。而原始时间序列xn的符号化表示为sn={s(1),s(2),…,s(n)}。其中sn通过将xn划分为q(q≥2)个不相交的区域并且将每个区域映射到一个符号s(i)∈{0,1,2,… ,q-1}=S,其中符号集S是有限个符号的集合,集合的大小为q。符号化过程所采用的空间划分方法对接下来的符号序列统计分析影响十分重大。在下一小节,将会详细介绍文中提出的概率密度符号化方法。
要将时间序列符号化,首先要选择符号集S的大小q,这是目前还有待研究的一个问题。若q太小将导致“粗粒化”过程当中原始时间序列有用信息丢失;若q太大将会导致计算效率大大降低。文献[3~5]选择q=2,3,4。为了阐述符号化的原理,在这里选取q=4简化说明
(1)
式中Ci为对xn进行空间划分得到的不相交集合。通过上述阈值函数,时间序列xn被转化符号序列sn。
在将获取的时间序列转化为符号序列之后,为了提取符号序列当中的特征信息需要对其编码[8]。首先选择一个标准长度L(L≥2),L个连续的符号组成一个字,每个字被编码成qL进制,这样就形成了新的编码序列。图1为L=4,q=4时符号序列的编码示意图。
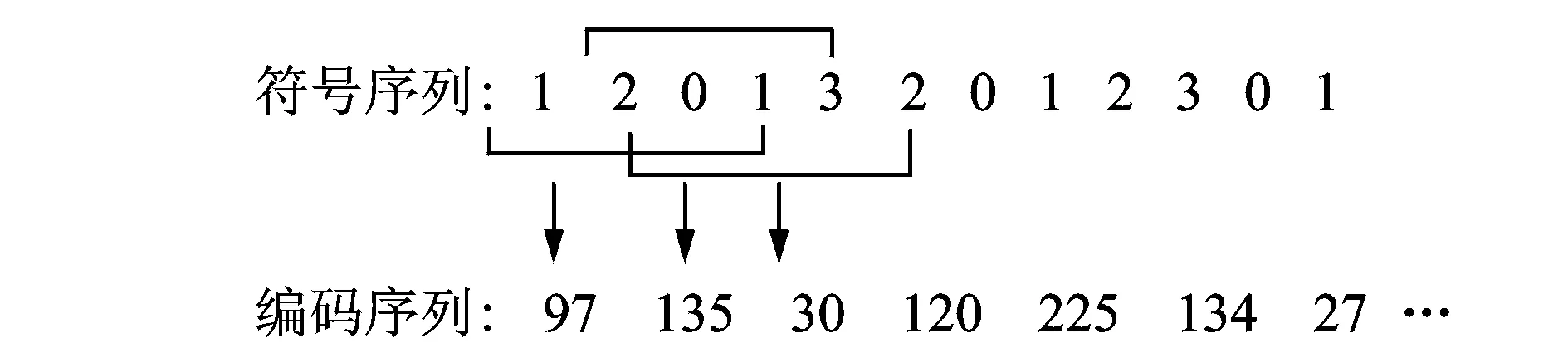
图1 编码示意图(L=4, q=4)
符号序列当中所含有的特征信息可以通过对编码序列进行统计学分析提取出来。对编码序列的分析方法有很多种,最常见的方法有信息熵法、标准差法。香农熵是通过计算编码序列的复杂度来确定系统的运行状态。香农熵越大则表示编码序列复杂度大,进而可以确定系统的不稳定性较大[9]。标准差法通过计算编码序列的标准差来衡量系统的运行状态,当机械系统运行正常时其编码序列的标准差较小,同时它会随着机械系统故障程度的加深而增大[10]。鉴于标准差法计算效率较高,本算法当中选取标准差法来对编码序列进行统计分析。
综上所述,符号化时间序列分析异常检测方法流程如图2所示。
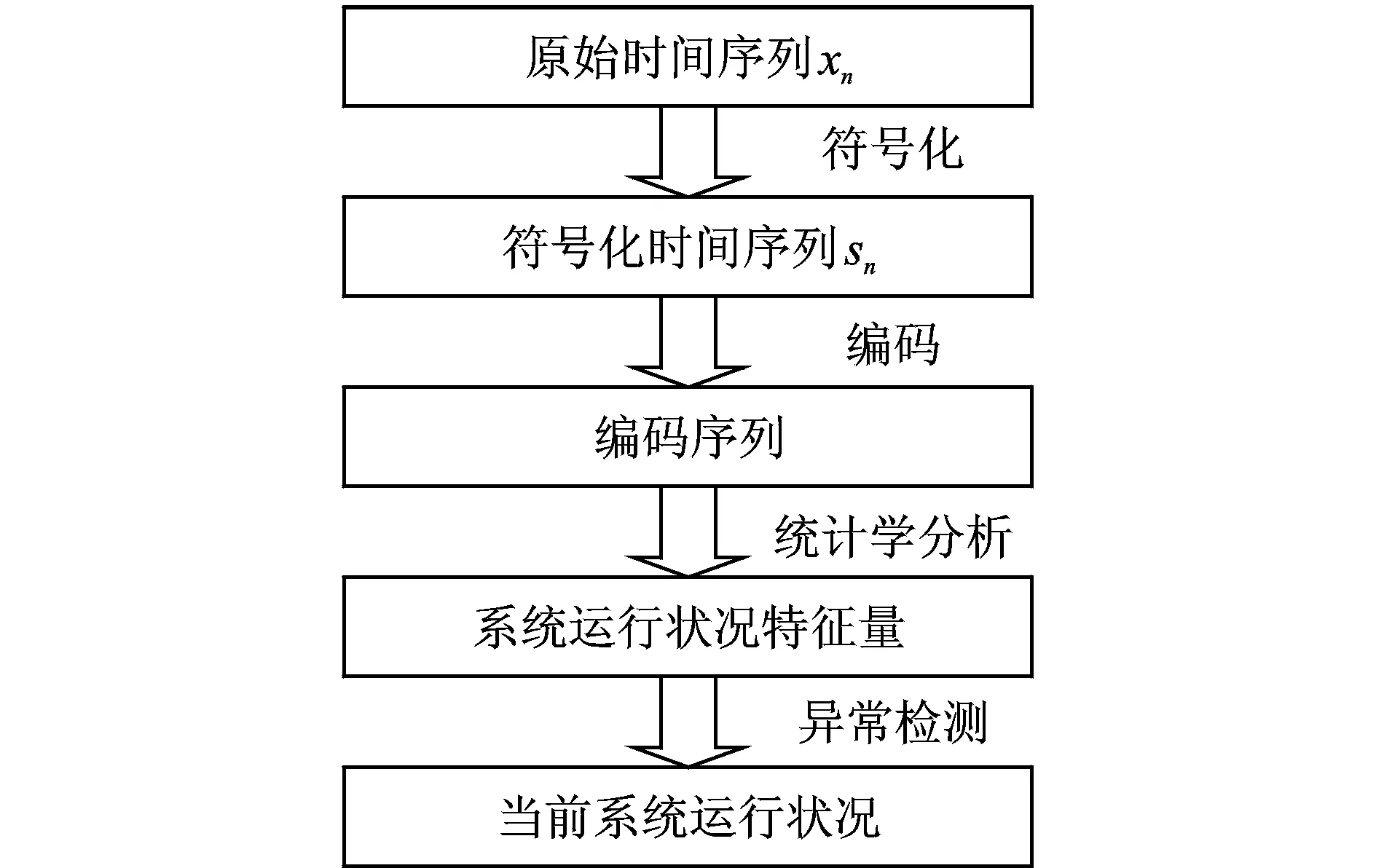
图2 符号化时间序列分析异常检测算法流程图
具体步骤如下所示:
(1)符号化:确定符号化当中符号集大小q,并选取划分方法将原始时间序列xn进行符号化。为了对比概率密度划分方法与其他符号化方法,本文中统一选取q=4。
(2)编码:确定编码字长L,并对符号序列sn进行编码。
(3)统计学分析:对编码序列进行统计学分析,本文中选取标准差为特征量。
(4)异常检测:将统计学分析中获得的表征系统运行状况的特征量与正常时系统运行特征量进行对比,从而判断当前系统运行状况。
2 概率密度划分方法
为了对原始时间序列进行概率密度划分,可以假设原始时间序列为连续型随机变量。然后对其进行数理统计分析,可以得到其概率密度函数f(x) 。密度函数f(x) 有如下性质:
(a)f(x)≥0;
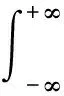
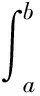
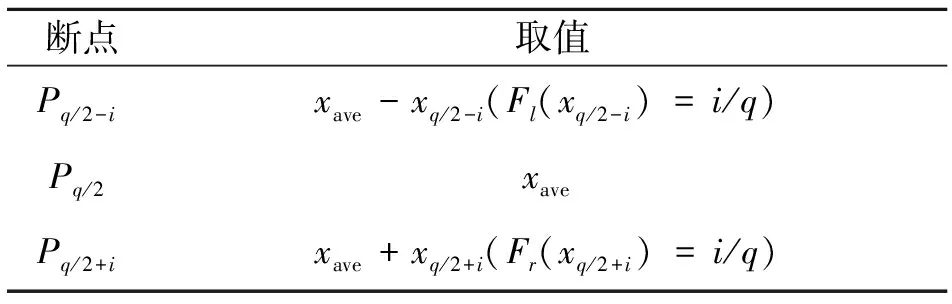
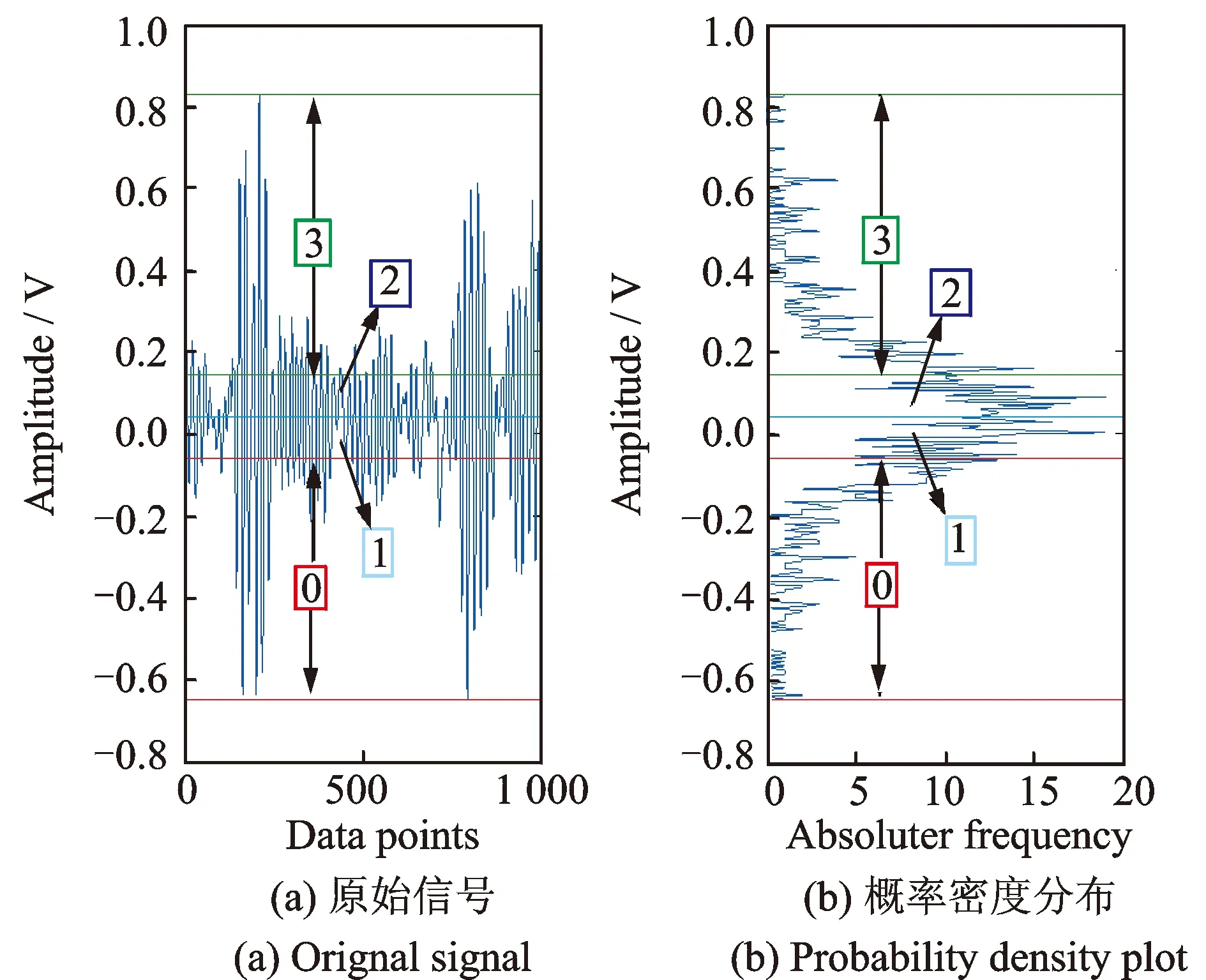
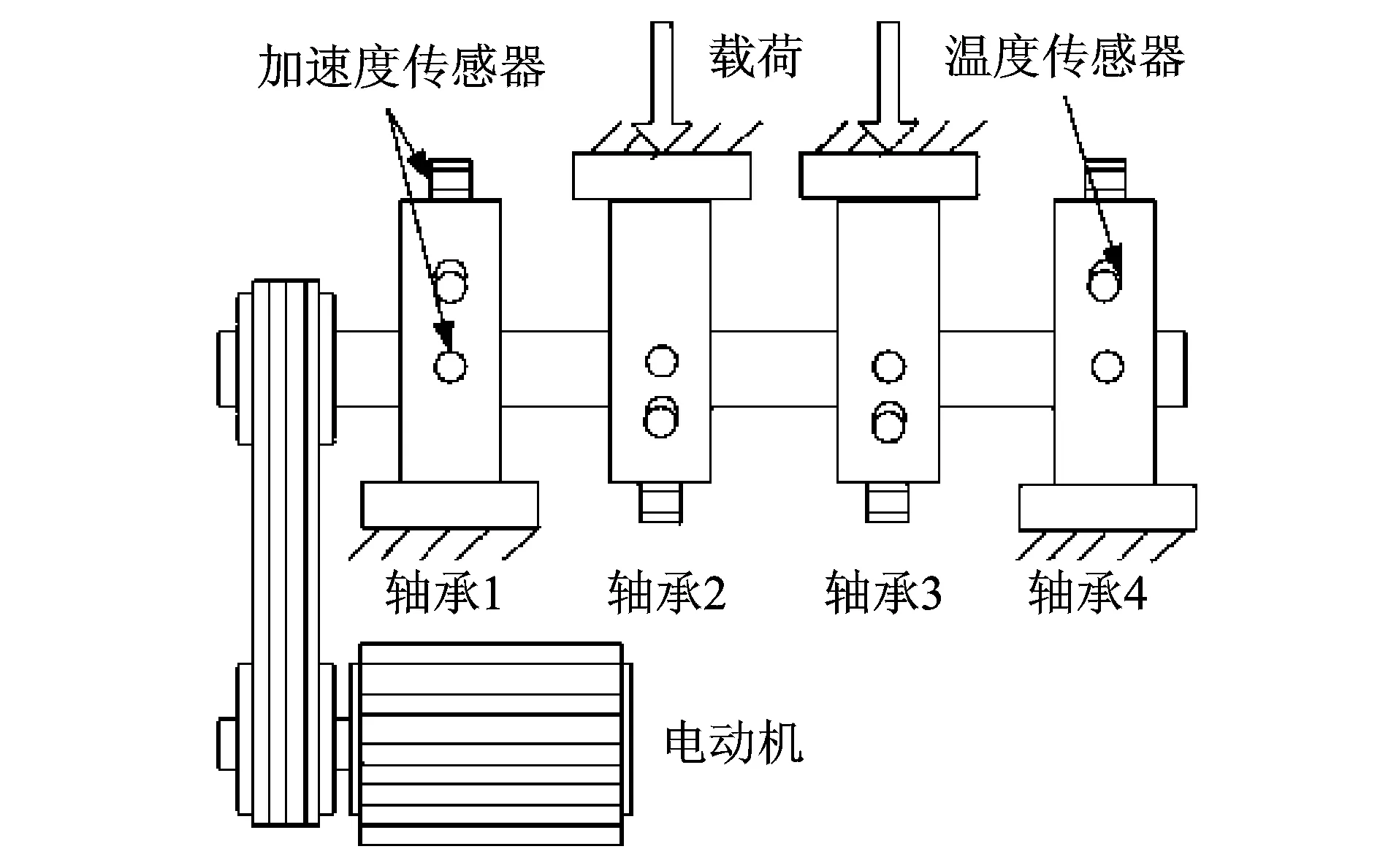
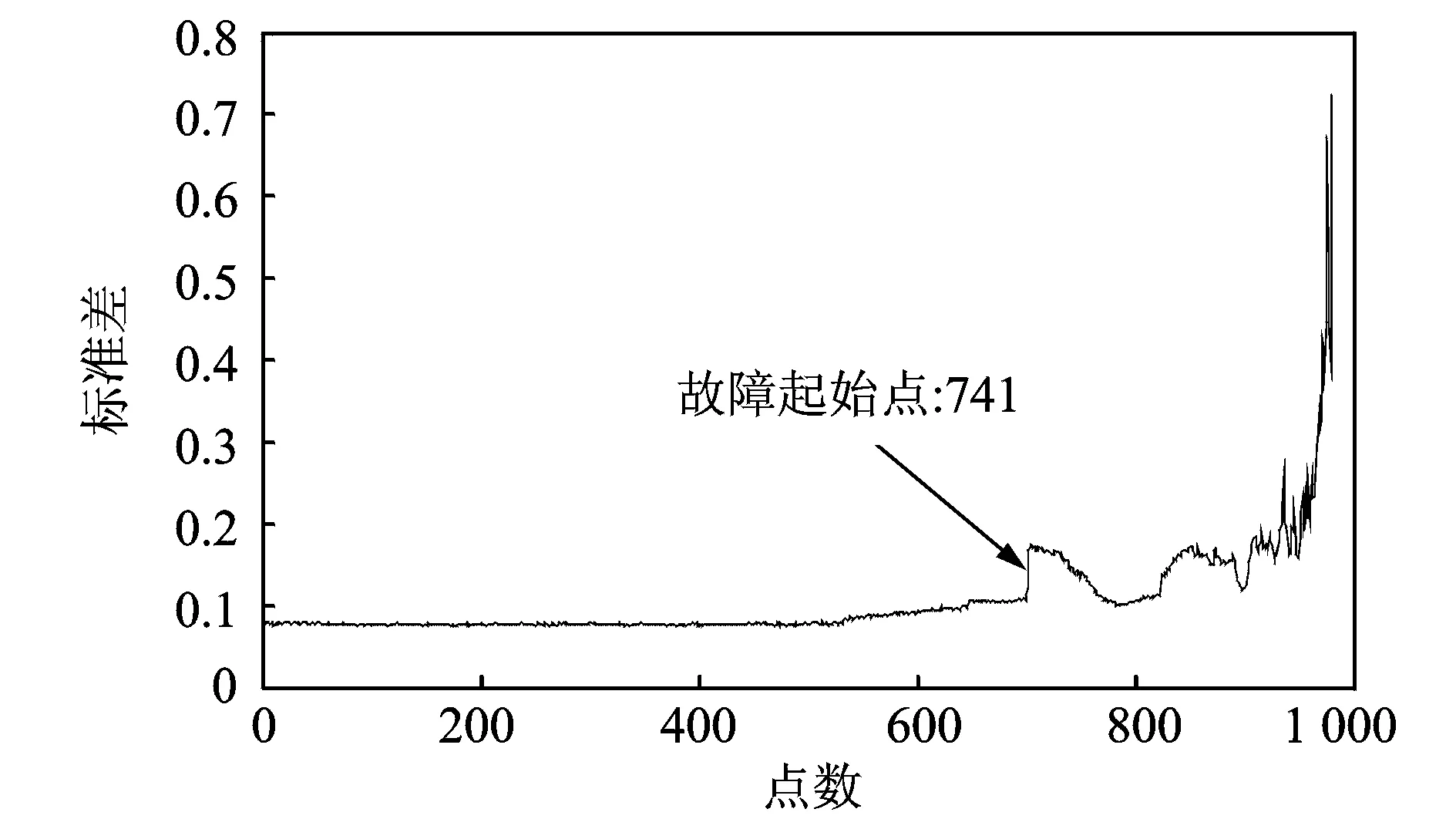
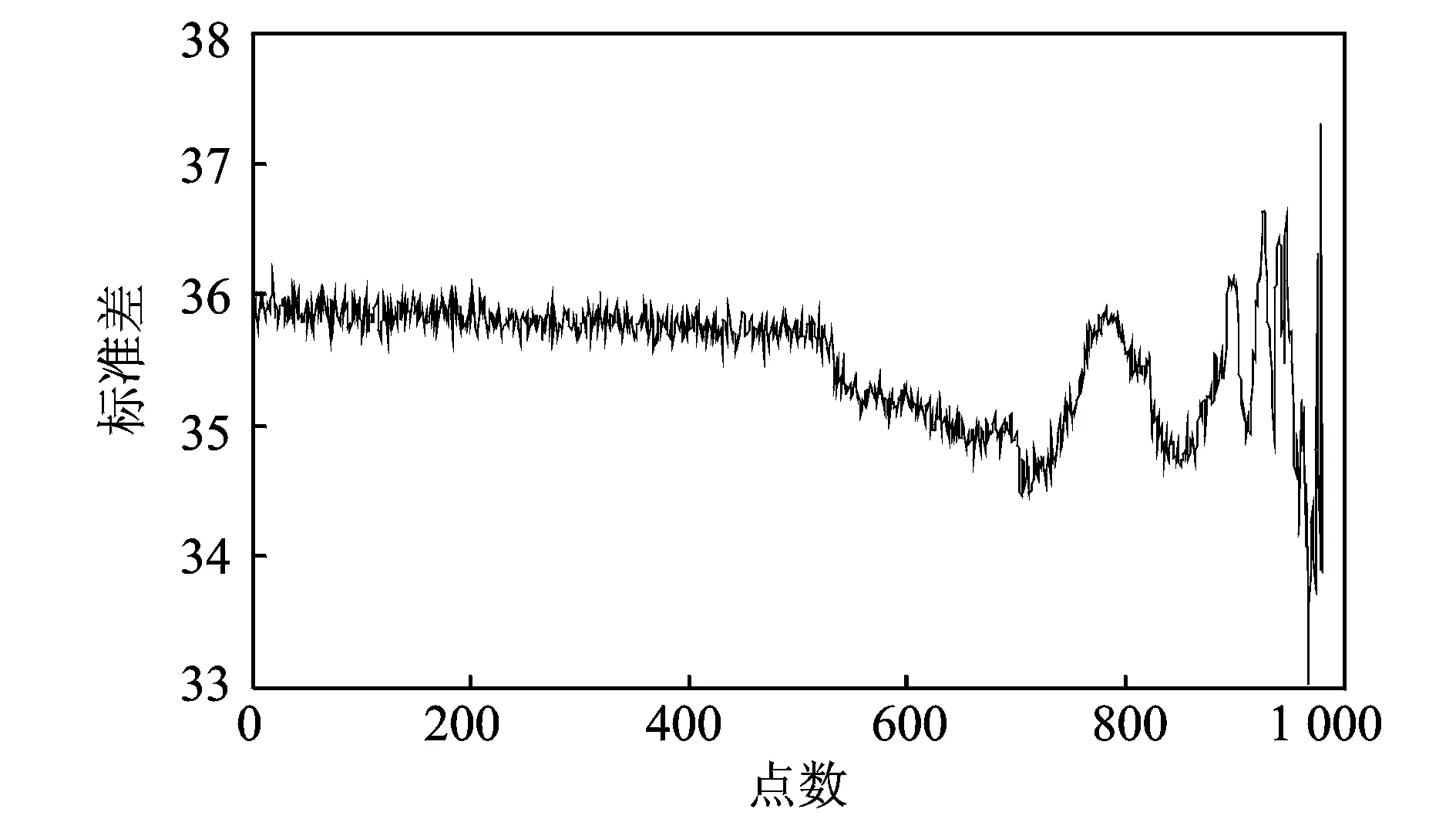
上述式子中,P(a 在确定概率密度函数f(x) 之后,选择时间序列的平均值xave作为中心点,可以按照下式分别计算右概率函数Fr(x) 和左概率函数Fl(x): (2) (3) 式中Fr(x) 表示时间序列当中取值在中心点xave到xave+x之间的概率。同理Fl(x)表示时间序列取值在(xave-x,xave]之间的概率。 接下来需要将原始时间序列进行空间划分, 即将其划分为q个区域。由于每个区域是连续的,所以其可以由两端“断点”来确定。“断点”是一系列点的集合,例如,概率密度划分P=[P1,…,Pi,…,Pq-2Pq-1],其中“断点”Pi到“断点”Pi+1为一个划分区域并且该区域的概率为1/q。根据符号集q的奇偶性,“断点”由两种不同的方式确定。如果q为偶数,按照表1来确定“断点”。如果q为大于2的奇数,其“断点”的确定方式如表2所示。 表1 偶数符号化断点 表2 奇数符号化断点 得到“断点”之后,空间划分的q个区域也就确定了。通过类似式(1)当中的阈值函数,原始时间序列将被转化为符号化时间序列。如图3所示为对实际机械振动信号进行概率密度划分的实例。其中图3(a)为原始信号,图3(b)为概率密度分布图。按照上述划分方法,信号被划分为4(q=4)个区间,每个区间分别表示为符号“0”, “1”,“2” ,“3”。 图3 概率密度划分示例 为了在实际实验中检验本划分方法的有效性,将基于概率密度划分的符号化方法应用在实际轴承故障数据上进行实验,并对结果进行分析。 轴承疲劳实验数据来自美国智能维护系统中心(IMS)[11],实验装置如图4所示。一个轴上安装了4套Rexnord ZA-2115 双列滚子轴承,每列滚子数量为16,滚子组节圆直径为75.501 mm,滚子直径为8.470 74 mm,接触角为15.17°。轴的转速保持2 000 r/min恒定不变,通过弹簧装置在轴上加载6 000 lb(2 721.554 kg)的径向载荷。所有轴承润滑固定,并且每个轴承座都安装2个PCB加速度传感器用来采集轴承的振动数据。振动信号由NI公司DAQCard-6062E数据采集卡每隔10 min采集一次,采样长度为20 480个点,采样频率为20 kHz。试验台中的4套轴承从2月12日11∶16∶18运行至2月19日06∶22∶39,一共采集到984个文件数据。在疲劳实验结束时,轴承1检测到外圈故障。 图4 轴承实验装置 对轴承1的振动数据进行基于概率密度划分的时间序列异常诊断。首先对轴承1的振动数据进行统计学分析,从而得到时间序列的概率密度分布。然后确定符号集q的大小。采用较大的q值划分之后的符号序列中含有更多的细节信息,但是这也会导致由噪声引起的错误符号增多,同时计算量也大大提高。采用较小的q值划分,则可能导致信息丢失[12]。合理的选取q值是很重要的,但是q值的选取不是本文主要研究内容。在本实验当中,参照以往文献经验性地选取符号集q=4。在完成对符号序列编码之后,每个文件编码序列的标准差如图5所示。编码序列的标准差越大,则其偏离正常状态越远。由于疲劳试验前期(前540个点)轴承处于健康状态,所以其编码序列标准差比较平稳并且处于较低水平。在541点时编码序列标准差检测到剧烈的增长,可以判断轴承故障在此时开始。编码序列的标准差随着故障程度的加深也逐渐增大。 为了检验基于概率密度划分符号序列分析算法的优劣,进行了对比实验2。在对比试验2中不采用符号序列分析方法,直接计算原始时间序列的标准差,其实验结果如图6所示。从图中可以看到在741点时标准差有剧烈增长,由异常检测原理可以判断该点为故障的起始点。与实验1的结果对比,检测到异常起始点滞后了200个点。本次对比实验可以证明基于概率密度划分的符号化方法对于系统中的异常更加敏感。 图5 基于概率密度划分符号序列分析结果 图6 原始时间序列标准差分析结果 对比实验3使用传统统一划分的STSA算法与本文方法进行比较。实验结果如图7所示。通过曲线可以观察到,当轴承处于健康状态时,曲线较为平稳。但是当异常发生时曲线发生剧烈的抖动,从而导致人们无法判断异常起始点。从本实验可以看到划分方法对于基于符号化时间序列分析异常诊断的影响,同时此实验结果也证明概率密度符号化方法相比统一划分方法更好。 图7 基于统一划分符号序列分析结果 在符号化时间序列分析当中,生成符号化序列这一步至关重要。本文提出了一种新颖的符号化方法,该方法利用原始时间序列的概率密度分布来对其划分,具有适用性强、符号化效果好的特点。同时将基于概率密度划分的STSA应用于实际轴承系统的异常诊断中。对比实验结果表明,相比直接标准差分析,本文提出的基于概率密度划分的符号化方法对于轴承的异常信息更加敏感,能够更早地发现故障。这对于故障的预防、轴承维护、安全生产具有重大意义。通过对比实验进一步发现,概率密度符号化方法相比于传统的统一划分在轴承的异常诊断当中更加有效、稳定。 本文当中也存在一些不足之处,例如未对符号集q的大小以及编码序列长度L进行细致的研究,只是根据以往文献经验性地取值。然而这些取值对与符号化时间序列分析具有很大的影响,这些问题需要更加深入的研究和验证。 参考文献: [1] 何正嘉, 陈进, 王太勇. 机械故障诊断理论及应用[M].北京:高等教育出版社,2010.He Z J, Chen Jin , Wang T Y. Theories and Applications of Machinery Fault Diagnostics[M]. Beijing:Higher Education Press, 2010. [2] 郭劲松, 卫武迪. 基于稀疏符号时间序列分析的转子碰摩故障早期检测方法[J]. 振动与冲击, 2008, 27(12): 148—150.Guo J S, Wei W D.Methods for identification and early detection of rub-impact fault in rotors based sparse symbolic time series analysis[J]. Journal of Vibration and Shock, 2008, 27(12): 148—150. [3] Ray A, Symbolic dynamics analysis of complex for anomaly detection[J]. Signal Processing, 2004, 84(7):1 115—1 130. [4] Rajagopalan V, Ray A. Symbolic time series analysis via wavelet-based partitioning[J]. Signal Processing, 2006, 86:3 309—3 320. [5] Lin J, Keogh E, Lonardi S, et al. A symbolic representation of time series with implications for streaming algorithms[A].Proceedings of the 8th ACM SIGMOD workshop on Research Issues in Data Mining and Knowledge Discovery[C]. ACM, 2003: 2—11. [6] 王妍, 徐伟. Lorenz 系统中时间序列的相空间重构方法与特性[J]. 振动工程学报, 2006, 19(2): 277—282.Wang Y, Xu W. The methods and performance of phase spacereconstruction for the time series in Lorenz system[J].Journal of Vibration Engineering, 2006, 19(2): 277—282. [7] Daw C S, Finney C E A, Tracy E R. A review of symbolic analysis of experimental data[J]. Review of Scientific Instruments, 2003, 74(2): 915—930. [8] Das G, Lin K I, Mannila H, et al. Rule discovery from time series[J]. Knowledge Discovery and Data Mining, 1998,98:16—22. [9] Tang X Z, Tracy E R, Boozer A D, et al. Symbol sequence statistics in noisy chaotic signal reconstruction[J]. Physical Review E, 1995, 51(5): 3 871—3 889. [10] Bishop C M. Pattern recognition and machine learning[M]. New York: Springer, 2006. [11] Qiu H,Lee J,Lin J,et al. Robust performance degradation assessment methods for enhanced rolling element bearing prognostics[J].Advanced Engineering Informatics,2003,17(3):127—140. [12] Finney C E A, Nguyen K, Daw C S, et al. Symbol-sequence statistics for monitoring fluidization[J]. ASME HEAT TRANSFER DIV PUBL HTD, 1998, 361: 405—412.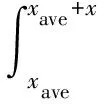
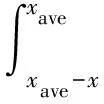

3 实验验证

4 结 论

