Crazy Climber算法与重采样技术在消除多普勒效应及列车轴承诊断中的应用

王 超， 孔凡让， 胡 飞， 刘 方

(中国科学技术大学精密机械与精密仪器系， 安徽 合肥 230022)

引 言

随着现代铁路运输的快速发展和不断提速，其安全性问题变得日益突出。轴承是火车上必不可少的重要零部件之一，而大多数旋转机械的失效都是由轴承故障和缺陷引起的[1～3],因此建立健全火车轴承的状态监测与故障诊断系统变得尤为重要。20世纪80年代，列车声音检测系统(ADBD)技术的发展在预报和诊断轴承失效和过热方面取得良好的效果[4]。ADBD通过在道旁设置固定麦克风阵列，当火车经过时麦克风阵列采集声音信号并传输至信号处理系统，由此实现火车轴承的监测与诊断，其相比于机载监视系统(OBM)[5]和热轴承检测系统(HBD)[6]有着经济实用、适应性强等优点[3]。

然而当列车高速运行经过ADBD时，其诊断的有效性将有所降低，其中一个重要的原因就是列车与麦克风阵列之间的高速相对运动引起的多普勒效应，多普勒效应会在时域和频域上对采集到的信号产生较大的畸变和频移，这无疑将严重影响诊断效果[7]。因此为了提高列车高速运行中麦克风采集到信号的可用性，进而提高列车轴承状态监测和故障诊断的有效性，多普勒效应的消除势在必行。

近年来，国内外许多学者针对多普勒效应的消除做了大量研究并取得相应的成果。杨殿阁等建立了基于测量面、辐射面和声全息面的运动学几何关系，提出了声源与测量信号之间的非线性时间映射方法，从而消除了多普勒效应[8]。但这种方法需要预先测量传感器与铁轨的垂直距离以及列车速度等参量，使得其在实际使用中受到了限制；Dybala提出了一种基于希尔伯特变换的面向干扰的动态信号重采样方法以消除道旁监测系统受到的多普勒效应的影响[7,9]，然而这种方法在频域处理时只能包含单一的频率谱线，这与实际使用环境中存在的宽带频率成分相矛盾；此外希尔伯特变换的端点效应也对此方法的有效性产生严重的影响。

针对上述两种方法存在的问题，提出一种基于短时傅里叶变换和Crazy Climber算法(STFT-CC)的瞬时频率估计方法，应用此方法得到拟合的瞬时频率曲线，结合莫尔斯理论得到信号重采样所需的各项参数，并针对多普勒效应进行运动学建模，确定时域重采样时间间隔，进而消除信号中多普勒效应的影响。此方法能够有效提取重采样所需各项参数，从而避免了对未知量的预测量。

文中首先介绍了声学运动学模型、时域重采样方法和基于STFT-CC的瞬时频率估计方法；然后针对提出的方法进行了信号仿真；最后将此方法应用于实际故障轴承的诊断中。仿真和实验结果均表明本文方法的可行性与有效性。

1 诊断方法和原理

1.1 诊断方法

消除列车轴承多普勒效应并进行故障诊断的方法主要分为五个步骤，即基于STFT的时频分析，基于CC算法瞬时频率估计，对估计得到离散时频点进行非线性拟合，基于时域重采样技术消除多普勒效应，包络分析得出诊断结果。图1给出了本文提出方法的流程图。首先对多普勒畸变信号进行STFT时频分析，从时频谱图上观察瞬时频率变化，估计CC算法阈值，然后利用CC算法对时频谱图上的各条瞬时频率脊线进行估计，并根据声学理论进行非线性最小二乘法拟合，得到连续的瞬时频率曲线，对拟合得到的连续瞬时频率做时域重采样，即可对原信号中的多普勒效应进行消除。最后，对去除多普勒效应的信号进行包络分析，分析包络谱图后可得到故障诊断结果。

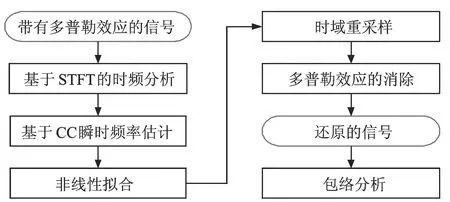
图1 消除信号多普勒效应流程图

1.2 时域重采样原理

消除多普勒效应最常用的方法是用不同的采样频率对原信号进行重采样，进而还原出不失真的信号，其中的关键就是确定重采样的时间序列。最近，Dybala提出了一种基于希尔伯特变换的面向干扰的动态信号重采样方法以消除多普勒效应[7]，这种方法需要已知被测对象的特征频率，而且其在频域处理时只包含有单一谱线。时域重采样方法与之相比具有明显的优势，由于其完全基于声学运动学模型，因此时域重采样方法更加易于理解和应用。

列车经过麦克风时的情况如图2所示，这里假定列车以恒定速度沿笔直铁轨运行，仅考虑单一声源和单一麦克风的情况。

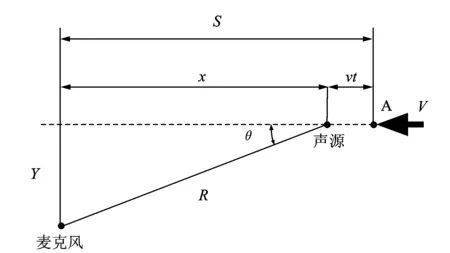
图2 列车经过麦克风示意图

由图2可知，在声源发声时刻与麦克风接收时刻之间存在一段延时，随着声源和麦克风之间距离的缩短，其延时时间将逐渐变短，这意味着信号在时间轴上被压缩了，因此信号频率提高了，反之当声源远离麦克风时，信号在时间轴上被拉伸，因此信号频率降低，这就是运动声源测量中多普勒效应的产生原因。

图2中点A即初始位置，此处时间为0。假设在时间为ts时，声源发出的信号幅值为x(ts)，此信号经过传播在时间tr时到达麦克风，因此有下式成立

tr=ts+Δt

(1)

式中 Δt即声音信号在空气中的传播时间，可由下式得到

(2)

式中c为空气中的声速(设为c=340 m/s)。R是声源与麦克风在发声时刻ts时的距离，将式(2)代入式(1)可得

(3)

式(3)建立了发声时刻ts和麦克风接收采样时刻tr之间的关系，因此重采样时间序列可通过式(3)的计算得到，式中参量Y,S和v可从1.3节中得到。

重采样的过程通过对原信号进行三次样条插值完成，如图3所示。图中tm为麦克风实际采样时间序列，tp为重采样时间序列，xp为原信号幅值序列，xr为校正信号的幅值序列。

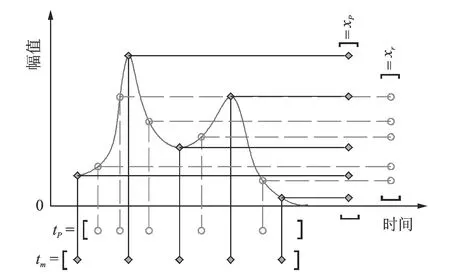
图3 重采样过程示意图

时域重采样的具体步骤如下：

(1)以声源在A点出发时刻为0时刻，校正麦克风采集信号时间原点，即tm=tr+R0/c，其中R0为出发时刻声源与麦克风之间的距离，c为声速。

(2)由式(3)计算得到tp，将tm代入式(3)中的ts，得到的tr即为tp。

(3)对离散的xp(tm)进行三次样条拟合，对拟合后的曲线利用tp插值。

(4)所得信号xr(tp)即为还原信号。

1.3 基于STFT-CC的瞬时频率估计

定义一个频率调制信号为

x(t)=Aexp(jφ(t))

(4)

则信号的瞬时频率定义为信号相位的一阶导数ω(t)=φ′(t)。信号的瞬时频率是一个非常重要的参量，其估计的准确程度关系到对其他信号参量的求取[10]。

自从Ville于1948年提出瞬时频率的概念以来，发展出许多计算和估计信号瞬时频率的方法，例如希尔伯特变换、分数阶傅里叶变换和Prony法等[11～14]，然而这些方法大都因频率估计效果不理想而在实际使用中受到限制。而基于STFT的瞬时频率估计以其线性时频变换、无交叉项等优点得到广泛应用，因此这里使用STFT获得信号的时频分布。此外，基于STFT的时频分布在信号瞬时频率变化较慢的情况下能够在后续的信号处理过程中表现出较为满意的效果。

获取信号瞬时频率的一般方法是求取信号时频分布的谱峰值，然而该方法不能同时提取多条瞬时频率曲线，且在高噪声和复杂工况环境下，时频分布谱峰检测法并不能给出理想的瞬时频率估计[15]。

Crazy Climber 算法是由Carmona 于1999年提出的[16]，该算法在一定程度上能够同时提取多个瞬时频率。在时频谱图上，信号的能量都集中在一些被称为脊线的地方，通过随机分布在该时频谱图上的质点受到脊线的吸引而建立的马尔可夫链。在提取脊的过程中，该算法将一系列按一定规则随机运动的点视为一种密度分布，所有的点在经过一定程度的移动以后形成整体上的密度分布图，然后将密度最为集中的区域指定为脊线的轨迹。

Crazy Climber 算法提取多脊线的核心思想是这样的[17]：在起始时刻时，一系列的质点(可称之为Climbers)随机的安排在时频分布图上，每一个质点可认为是分布密度的度量；然后每一个质点在时频面上按照一定的规则进行移动，而这个规则取决于该质点以及该点下一时刻可能在时频分布的非零矩阵M的值；经过移动后，质点逐渐被时频分布图上脊所在的位置吸引而逐渐聚集，就像在爬山一样。类似于模拟退火方法[18]，整个系统也是有一个设定的初始温度，并且温度逐渐降低，随之各个可以移动的点逐渐稳定下来，聚集在脊所在的位置上。

假设时频分布矩阵M的大小是B×U，M(j,k)表示在时频分布上位置为(j,k)的值，其中j=1,2,…,B为水平方向，k=1,2,…,U为竖直方向。所有质点独立地依据规则移动，该规则描述如下：

在初始时刻t=0，质点总数设为N，它们平均分布在网格上Γ={1,2,…,B}×{1,2,…,U}。质点的初始位置用Xα(0)表示，其中α=1,2,…,N作为质点的标记。另外，初始温度设为T(0)。

在某时刻t时，某一个质点停留在位置上Xα(t)=(j,k)，那么它的下一个位置Xα(t+1)=(j′,k′)由两个条件确定。首先是水平方向，如果2≤j≤B-1，那么j′=j-1或者j'=j+1各占50%的概率，即该点以相同的概率向左或向右移动一格；如果该质点刚好处于时频分布的边际位置，那么该质点须向边际的反方向移动，即如果j=1，质点向右移动一格j′=j+1，反之如果j=B，质点向左移动一格j′=j-1；因此在水平方向移动后，该质点的位置变为(j′,k)。然后是竖直方向，与水平方向一样质量向上或向下移动的概率相同(边际情况处理与水平方向相同)，但是它也可能不做移动而停留原位置，如果M(j′,k′)>M(j′,k)，质点须移动，即Xα(t+1)=(j′,k′)；反之，这个移动按照概率

(5)

执行，按照概率(1-pt)不执行。同时，系统温度将更新为T(t+1)。

当系统温度的值低于某个设定的阈值时，这个迭代移动过程结束。

当整个迭代过程结束后，需要对网格上的每个点进行度量，度量的方式存在两种。第一种称之为均值度量，在某一时刻，考虑每个移动点相当于质量为1/N的质点，则可以度量该网格点在t时刻的度量值为

(6)

第二种度量方式称之为加权度量，该方式考虑到了将原始的时频分布平面上的数据用来对上式的结果进行加权，期望不仅能提取到脊所在的正确的位置，而且脊上参数的变化能更加贴近原来的时频平面上参数的变化规律。该网格点在t时刻的加权度量值为

(7)

因为每个可移动点的运动是一个随机的过程，因此上述测量值也是一个随机量，为了对每个网格点进行最终的度量，需要用这个随机量的均值来代表度量值，因此有

(8)

式中T为总时间长度。基于上述算法的结果，将度量值相对突出的这些点连接起来实现对所有IF的提取。

考虑到噪声和脊线边缘的影响，需要设定一个阈值用于将脊线从低度量值中区分出来。

(9)

式中SH表示设定的阈值，由于一般情况下噪声和脊线边缘的测度值远小于脊线处的测度值，因此可以使用整个分布测度值的均值或是均值的倍数作为阈值。经过上述处理后的脊线点已经清晰显示出来，考虑瞬时频率是沿着时间轴方向缓慢变化的曲线，从网格左端时刻开始沿着时间轴提取与前一刻脊点频率坐标相近的脊线点作为下一时刻脊点频率值，并将二者连接成一条脊线，重复这一过程直到所有的脊线均被找到。

另外一个值得注意的是，由于一些具有较高能量的随机噪声可能在脊线提取过程中被凸显出来，形成局部极值点孤立的存在于时频矩阵中，但是由于随机噪声脊线的长度较信号脊线的长度要短很多，因此在提取IF时须设定一个最短长度，小于该长度的脊线认为是随机噪声，从而消除这些局部高能量随机噪声对脊线提取的影响。

2 仿真信号处理实例

2.1 构造仿真信号

图2给出了信号发生与接收的示意图，在列车速度为亚声速的情况下，考虑列车轴承声源为单极子点声源，并且传播介质为理想流体即不存在粘滞性，没有能量损耗。根据莫尔斯声学理论[19]，从波动方程和运动关系出发，略去影响甚微的高阶项后可以推导得出以下公式

(10)

式中P为麦克风处采集到的声压，q=q0·sin(2πf0t)为单极子点声源质量总流率，q′=∂q/∂t，R为发声时刻声源与麦克风之间的距离，θ为发声时刻声源与麦克风连线与声源运动方向之间的夹角，M=v/c为声源运动的马赫数。由式(10)可推导出信号频率的表达式[9]

f=f0·

(11)

式中Y为铁轨与麦克风的垂直距离，S为声源起始点与麦克风之间的水平距离。

仿真中采用3个频率彼此非常接近的信号(f1=1 000 Hz,f2=1 100 Hz,f3=1 200 Hz)以保证其不会被带通滤波器所提取。预先给定的参量为：S=8 m,Y=2 m,c=340 m/s和v=20 m/s，仿真信号的时域波形如图4所示。

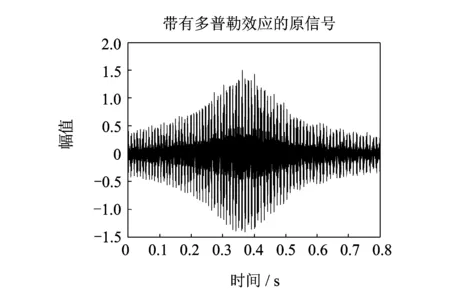
图4 仿真信号

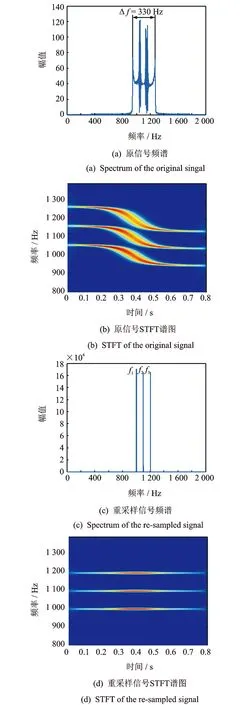
图5 原信号与重采样信号

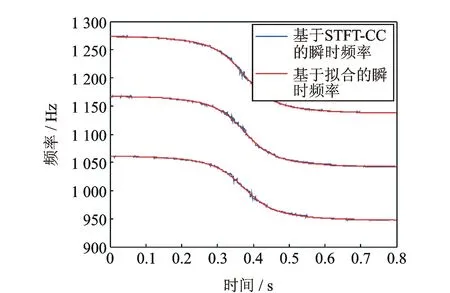
图6 仿真信号瞬时频率与非线性拟合曲线

2.2 仿真结果

对仿真信号以4 000 Hz频率进行采样，图5(a)给出了原信号的频谱图，从中可以明显看到由多普勒效应引起的频移。图5(b)给出的STFT时频分布图也明显受到了多普勒效应的影响。 对仿真信号进行CC算法处理，以3倍整体测度值的均值作为处理阈值，处理得到的离散瞬时频率及其非线性拟合曲线如图6所示。选择f2=1 100 Hz的畸变信号，根据拟合曲线并结合式(11)可以得到f0,Y,S和v四个参量，其值在表1中给出。将得到的参量代入式(3)可得到重采样时间序列tr，由此对原信号进行重采样，经过重采样后信号的频谱和STFT谱图分别如图5(c)和5(d)所示，可以看到经过本文方法处理后的信号已经完全消除了多普勒效应的影响。由此可以看出，在处理包含多种频率成分的多普勒畸变信号时，本文方法无需预测量其他参数，即可得出正确的诊断结果，相比杨和Dybala的方法具有明显的优势[7～9]。

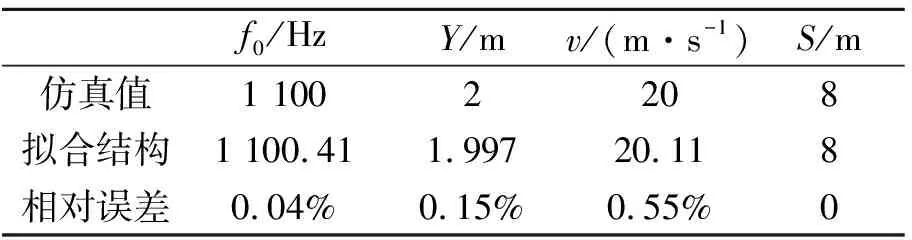
表1 非线性曲线拟合参数与给定参数的比较

3 实验验证

本实验平台由作者所在团队自主设计开发，被测轴承型号为目前列车上广泛使用的NJ(P)3226X1，声音采集采用B&K公司生产的4944-A型麦克风，对被测轴承的内圈和外圈分别进行线切割，宽度均为0.18 mm，如图7所示。实验分两组进行，分别采集内圈故障轴承和外圈故障轴承的声音信号，图8(a)为故障轴承测试平台，轴承由电机驱动(转速为1 430 r/min)，在一定负载作用下(负载为3 t)产生声音信号。使用NI公司开发的数据采集系统(DAS)采集数据信号(采样频率为50 kHz)。图8(b)为实验场景，测试平台和扬声器被固定在移动的汽车上，汽车沿直线以恒定速度行驶，产生的声音信号被固定的麦克风采集。

图7 内外圈故障

图8 实验平台和实验过程

被测轴承的具体参数如表2所示，对于轴承内外圈单点故障特征频率可有下式获得

(12)

式中fr为轴承旋转频率，即1 430 r/min，由此可计算得到外圈故障特征频率为138.7 Hz，内圈故障特征频率为194.8 Hz。

分析实验信号和消除多普勒效应的具体步骤如图1所示。然而实际实验环境远比仿真情况复杂，实验环境更易参杂各种频率的噪声，因此这里仅选择频率成分相对较高的部分进行分析。此外实验中的采样频率非常高，如果直接对采样所得数据进行分析，显然超出了现有计算机的能力范围。对图9中采集到的轴承外圈故障信号进行频谱分析，从图10(a)中可看到，外圈故障轴承的频率成分在1 000～2 000 Hz部分相对较高，因此这一部分是大家感兴趣的部分，所以选择2 500 Hz以下的频率成分进行分析，对信号低通滤波后以5 000 Hz进行降采样。为了更清楚地观察信号的时频分布，图11(a)给出了频率为800～1 600 Hz之间的STFT时频分布，从图中可以看到存在2条瞬时频率曲线，经过STFT-CC方法处理后的瞬时频率估计曲线如图11(b)所示，由非线性拟合得到的4个未知参量分别为f0=1 251 Hz;v=30.26 m/s;Y=2 m以及S=6 m，由此可以根据1.2节中介绍的时域重采样原理确定重采样时间序列，对原信号重采样后即可消除多普勒效应，图11(c)给出了去除多普勒效应后的信号STFT谱图，对比图11(a)，可以看到由多普勒效应引起的频移已得到较大的改善。

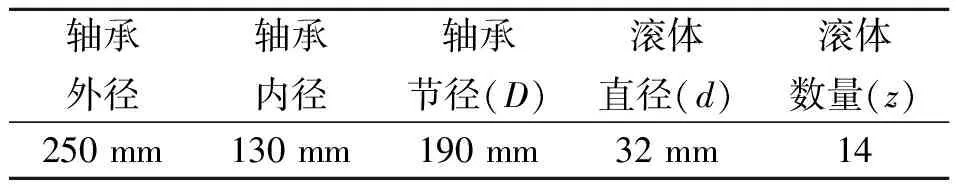
表2 NJ(P)3226X1轴承参数

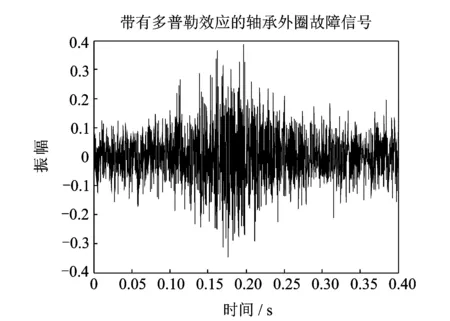
图9 列车轴承外圈故障信号

重采样后信号的频谱图和包络谱图如图10(c)和(d)所示，图中得到的轴承外圈故障特征频率为fo=138.3 Hz，与理论值138.7 Hz非常接近，而在原信号包络谱图10(b)中却由于多普勒效应的存在而不能得到正确的诊断结果。因此本实验验证了本文方法去除信号多普勒效应的有效性。

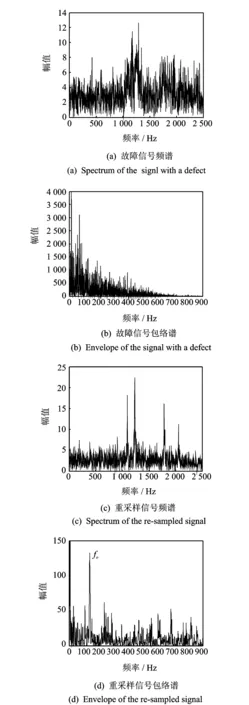
图10 外圈故障轴承信号频谱分析

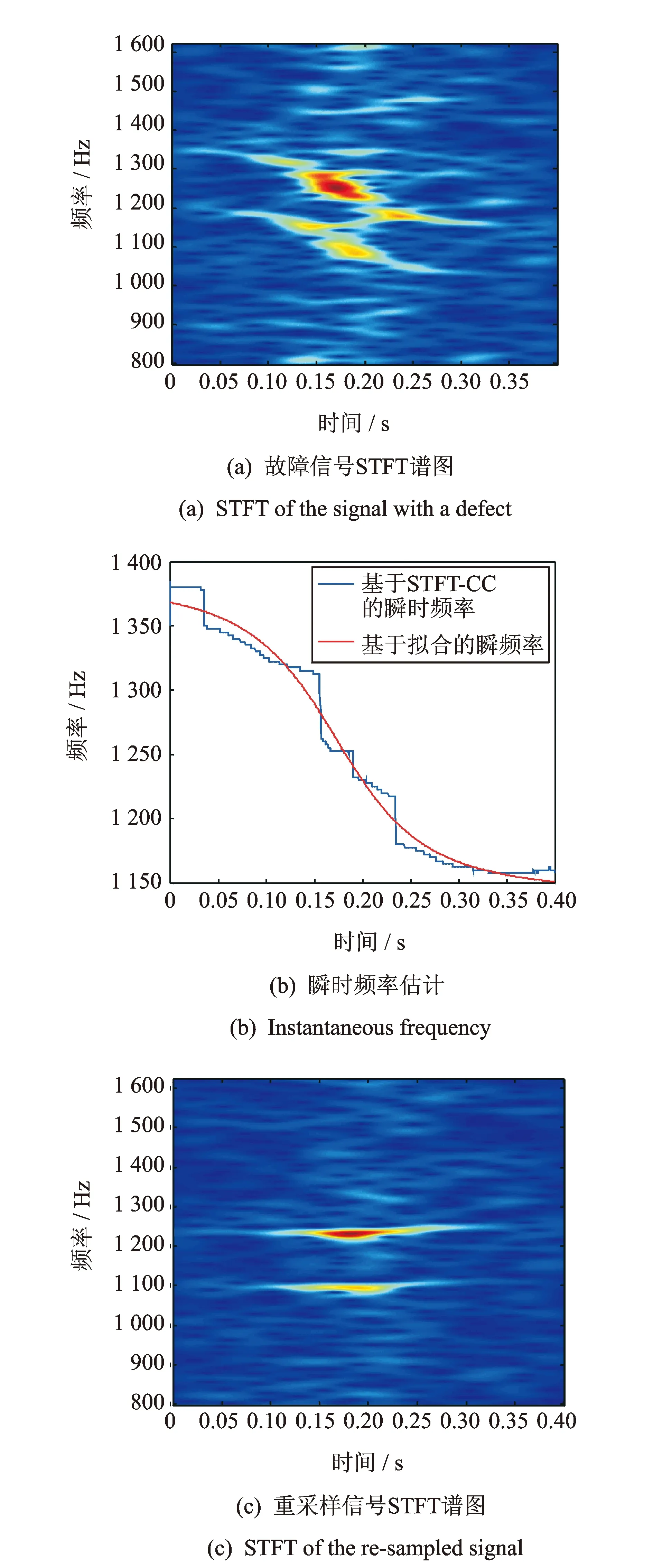
图11 外圈故障信号瞬时频率估计

对于内圈故障轴承信号的处理与外圈故障轴承信号的处理极为相似，这里就直接给出分析结果而不再赘述。图(12)为采集到的内圈故障轴承的时域信号。从图13(a)的频谱图中可以确定感兴趣的频带范围：1 300～2 100 Hz，与之对应的瞬时频率估计如图14所示。图13(b)为原信号的包络谱图，从中仅能得到轴承的旋转频率fr，而故障信息由于多普勒效应引起的频带展宽而被湮没了，因此对信号进行包络分析不能给出有效的故障诊断信息。而在重采样后信号的包络谱图13(d)中，由于多普勒效应的明显降低，使得故障信息集中地体现出来，可以明显地看到内圈故障特征频率fi=194 Hz，其与理论值194.8 Hz很接近。同时从图14(c)中也可以看出信号的多普勒效应得到了有效的去除。因此轴承内圈故障的实验再次表明了本文方法的有效性；同时实验的结果也再次显示了本文方法相比现有的两种多普勒校正方法在适用范围和可操作性上的明显优势。

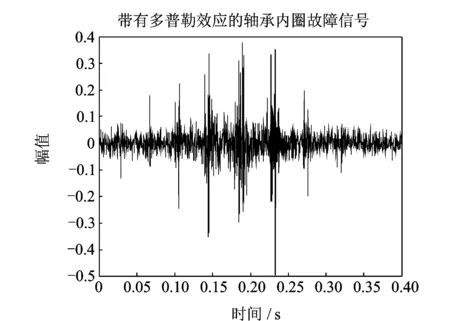
图12 列车轴承内圈故障信号

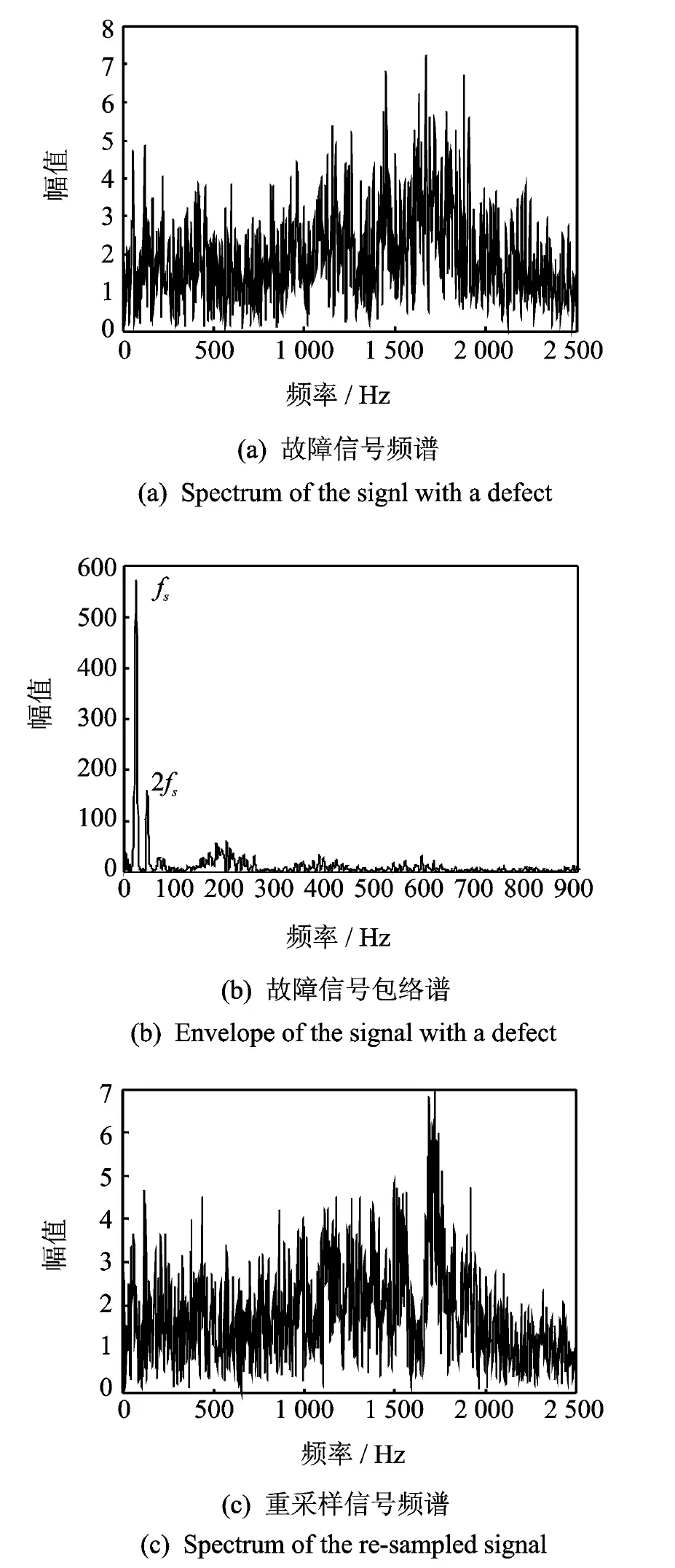
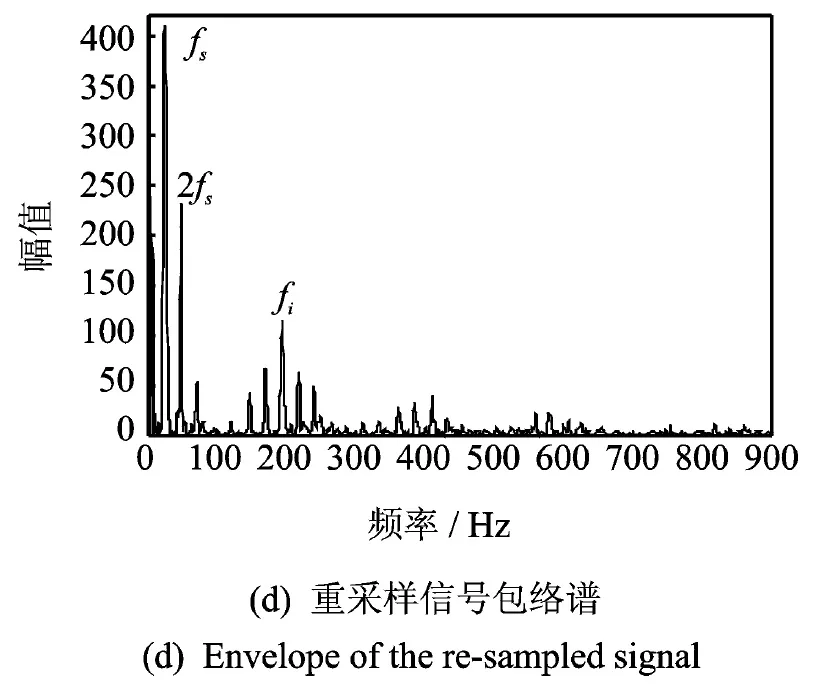
图13 内圈故障轴承信号频谱分析

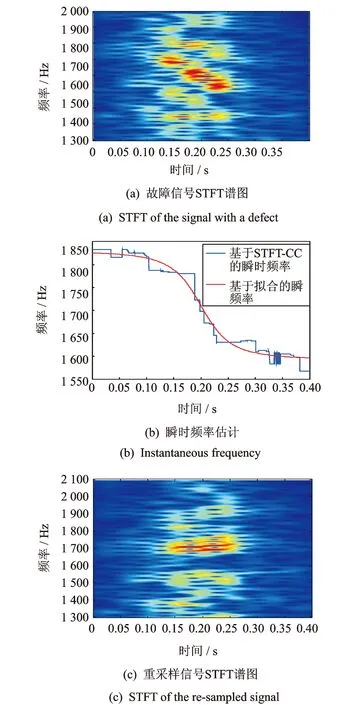
图14 内圈故障信号瞬时频率估计

4 结 论

本文提出了一种基于STFT-CC时频估计和时域重采样去除多普勒效应的方法，以此提高列车道旁轴承故障诊断的诊断效果。文中首先介绍了时域重采样理论和STFT-CC算法。STFT-CC可以通过非线性拟合的方式同时获取多个信号的时频估计曲线，这很好地解决了带通滤波器不能同时获得多条瞬时频率曲线的问题，避免了希尔伯特变换方法中存在端点效应的缺点；最后根据获得的时频曲线推导出曲线的对应参数，将其应用于时域重采样原理，可以得到重采样时间序列。因此时域重采样的过程不需要对其他参量进行预测量，大大提高了诊断的可行性和稳定性。

文中以3个频率彼此相近的信号对本文方法进行了仿真，并在实际测试平台上对外圈故障和内圈故障的轴承分别进行了实验，仿真和实验结果表明了本文方法在去除多普勒效应和道旁轴承故障诊断方面的有效性，展现了本文方法相比现有方法的优势所在。

参考文献：

[1] Xavier C, Fabrice B, Jean P D. Early detection of fatigue damage on rolling element bearings using adapted wavelet [J]. Trans. ASME Journal of Vibration and Acoustics, 2007, 129(4):495—506.

[2] Lei Yaguo, He Zhengjia, Zi Yanyang. Application of a novel hybrid intelligent method to compound fault diagnosis of locomotive roller bearings [J]. Trans. ASME Journal of Vibration and Acoustics, 2008, 130 (3):1—6.

[3] Yan Ruqiang, Gao R. Rotary machine health diagnosis based on empirical mode decomposition [J]. Trans. ASME Journal of Vibration and Acoustics, 2008, 130(2):021007.

[4] Choe H C, Wan Y, Chan A K. Neural pattern identification of railroad wheel-bearing faults from audible acoustic signals:comparison of FFT, CWT and DWT features [J]. SPIE Proceedings on Wavelet Applications, 1997, 3 087:480—496.

[5] Sneed W H, Smith R L. On-board real-time bearing defects detection and monitoring[A]. Proceedings of the 1998 ASME/IEEE Joint Railroad Conference[C]. Philadelphia,1998:149—153.

[6] Barke D, Chiu W K. Structural health monitoring in the railway industry:a review [J]. Structural Health Monitoring, 2005, 4:81—93.

[8] Yang Diange, Wang Ziteng, Li Bing, et al. Quantitative measurement of pass-by noise radiated by vehicles running at high speeds [J]. Journal of Sound and Vibration, 2011, 330:1 352—1 364.

[10] Djurovic′ I. Viterbi algorithm for chirp-rate and instantaneous frequency estimation [J]. Signal Processing, 2011, 91:1 308—1 313.

[11] 张旻,程家兴,樊甫华,等.利用Hilbert变换提取信号瞬时特征参数的问题研究 [J]. 电讯技术,2003,4:44—48.Zhang Min, Cheng Jiaxing, Fan Puhua, et al. Study on the problems in extracting instantaneous characters of signals based on Hilbert transform [J]. Telecommunication Engineering, 2003,4:44—48.

[12] Wang Yanxue, He Zhengjia, Zi Yanyang. A comparative study on the local mean decomposition and empirical mode decomposition and their applications to rotating machinery health diagnosis [J]. Trans. ASME Journal of Vibration and Acoustics, 2010, 132(2):021010.

[13] 赵义正,杨景曙.基于分数阶Fourier变换的瞬时频率估计方法 [J]. 安徽大学学报(自然科学版),2005, 29(1):44—49.Zhao Yizheng, Yang Jingshu. A method of instantaneous frequency estimation based on fractional Fourier transformation [J]. Journal of Anhui University Natural Science Edition, 2005, 29(1):44—49.

[14] 王磊,郝士琦,戎雁. 瞬时频率的Prony方法提取及MATLAB实现 [J]. 计算机仿真, 2008,25(2):303—305,309.Wang Lei, Hao Shiqi, Rong Yan. Prony method for instantaneous frequency detection and its implementation based on matlab[J]. Computer Simulation,2008,25(2):303—305.

[15] 赵晓平,赵秀莉,侯荣涛,等. 一种新的旋转机械升降速阶段振动信号的瞬时频率估计算法 [J]. 机械工程学报, 2011, 47(7):103—108.Zhao Xiaoping, Zhao Xiuli, Hou Rongtao, et al. A new method for instantaneous frequency estimation of run-up or run-down vibration signal for rotating machinery [J]. Journal of Mechanical Engineering, 2011, 47(7)：103—108.

[16] Carmona R A, Hwang W L, Torresani B. Multiridge detection and time-frequency reconstruction [J]. Signal Processing, 1999, 47(2):480—492.

[17] 张晓冬,王桥,吴乐南. 用于信号特征提取和重建的脊提取算法 [J].电子与信息学报, 2003, 25(7):878—883.Zhang Xiaodong, Wang Qiao, Wu Lenan. Characterization extraction and reconstruction of signal by the ridges of continuous wavelet transform [J]. Journal of Electronics and Information Technology, 2003, 25(7):878—883.

[18] 丁立新,康立山,陈毓屏,等. 演化计算研究进展 [J]. 武汉大学学报(自然科学版), 1998,44(5):561—568.Ding Lixin, Kang Lishan, Chen Yuping, et al. Research development of evolutionary computation [J]. Journal of Wuhan University (Natural Science Edition), 1998, 44(5):561—568.

[19] Morse P M, Ingard K U. 理论声学(下册)[M]. 杨训仁,吕如榆,戴根华,译. 北京:科学出版社, 1986:822—850.