运用数值迭代的动载荷识别算法

徐 菁， 张 方， 姜金辉， 浦玉学， 蒋 祺

(南京航空航天大学机械结构力学及控制国家重点实验室， 江苏 南京 210016)

引 言

在动力学问题研究中，准确知道结构的动载荷是非常重要的。动载荷识别技术主要发展了频域和时域两类载荷识别方法，通过时域法识别的载荷是一个载荷时间历程，可以直观了解载荷随时间的变化规律，更适用于工程实践。张方等用广义正交多项式特征技术建立载荷识别模型[1],解决了复杂结构的分布动态载荷识别问题。秦远田采用矩量法基函数来拟合未知动载荷[2]，将载荷识别转化成为在广义正交域中求解基函数拟合系数的问题。Allen和Carne采用SWAT方法对冲击载荷进行识别[3]，该方法可以同时识别稳态动态载荷与冲击型载荷。Gunawan等提出采用正则化二次样条函数来拟合冲击载荷[4]，利用基于L曲线的TSVD方法求解动载荷。Chen和Lee利用模态叠加正交技术获得梁的状态方程[5]，通过在线基于自适应权系数的递归算法来识别作用于桥梁结构的动态载荷，该方法具有较好的跟踪性能和误差估计特性。Mao和Guo将激励力描述为基函数与权系数之积的和[6]，为避免得到不稳定的解，在求解权系数的过程中，他们采用了基于GCV准则的Tikhonov正则化方法，在实验室中通过该方法来识别无人机机翼的瞬态冲击激励。韩旭等将动态载荷表示为一系列的脉冲或者阶跃函数的叠加[7]，并运用零相位滤波器、正则化技术和优化策略来实现载荷的稳定重构。高峰、李德武在Newmark法求解运动平衡方程的基础上[8]，推导了求解振动荷载的公式，提出由结构对振动荷载的反应求振动荷载时程的有限元方法。姜金辉等根据谱分解的思想[9]，提出多点任意相关的随机载荷识别方法，指出病态发生的原因和相应对策，提高了识别精度。Lin采用了广义卡尔曼滤波器以及基于常权系数的递归最小二乘法[10]，对单自由度非线性系统进行载荷识别，该方法能够较准确地估计正弦激励和多种冲击激励，并具有较好的抗噪性能。其后，他采用线性化卡尔曼滤波器以及基于自适应权系数的递归最小二乘法来识别非线性系统的时域载荷[11]，并将两种方法进行了对比，验证了后者的识别精度更高。Lee提出采用智能模糊权系数以改进自适应权系数的缺点[12]，识别结果表明智能模糊权收敛性好，能够有效降低测试误差、模型误差和仪器偏差的影响，且跟踪能力好。Lee和Chen在假设回转机械为刚体的基础上[13]，提出采用智能模糊权方法估计动态载荷。

本文对Wilson-θ反分析法的推导过程做了理论分析，找出其算法发散的原因。针对该原因提出了一种新的数值迭代修正方法，从数学上证明了修正的可行性，并且运用仿真和实验结果证明了修正算法的收敛。

1 Wilson-θ反分析法研究

Wilson-θ法是线性加速度法的扩展，在t至t+θΔt的时间区间内利用了线性加速度假设，并且计算得到系统的动力学方程。经严格数学证明，Wilson-θ法具有良好的数值稳定性，取θ>1.37即可保证结果无条件收敛，实际计算中一般取θ=1.4。文献[14]运用反问题的有限元方法[8]，推导得到一种反分析法来进行载荷识别。

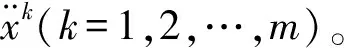
在t+θΔt时刻的系统拟静力方程为

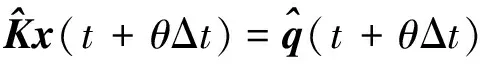
(1)

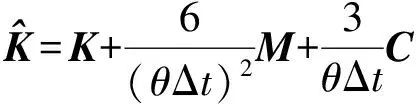
式(1)可分开写为

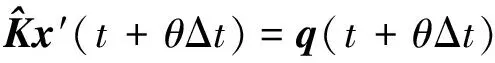
(2)

(3)

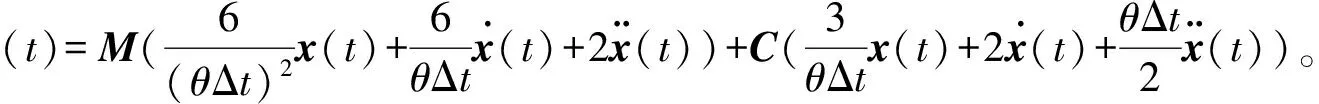
假设在每一微小的时间段内，可视为线弹性问题，根据叠加原理，有

x(t+θΔt)=x′(t+θΔt)+x″(t+θΔt)

(4)

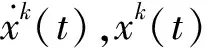
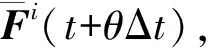
(5)

引入位移系数，得到如下方程

(6)

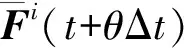
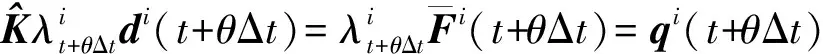
(7)

(8)

所以，式(2)的解满足下列线性关系

(9)

由式(4)得

xk(t+θΔt)-(x″(t+θΔt))k=v

(10)

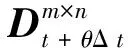
(11)

求出λt+θΔt后，根据式(5)，可以求出t+θΔt时刻的动载荷值qi(t+θΔt)，由于载荷qi(t)已知，故可得

qi(t+Δt)=(qi(t+θΔt)-qi(t))/θ+qi(t)

(12)

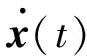
2 利用二分法迭代修正

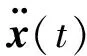
对于单点输入模型，可以采用二分法迭代对每一步的识别力进行修正。运用二分法迭代，必须先确定含根区间。由Wilson-θ法可知

(13)

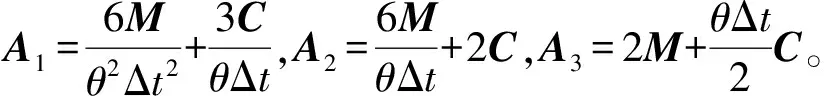
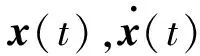
(14)

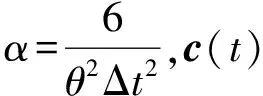
(15)

于是

(16)

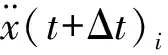
(17)

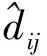
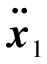
(18)

化简得

(19)

对gi(f)求导

(20)

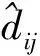
首先由Wilson-θ反分析法，得到识别力的时间序列q(t)。对于时间点tm，设其对应的载荷为q(tm)，令

a1=-rq(tm)，b1=rq(tm)

式中r为区间放大倍数，且满足g(a1)g(b1)<0，则[a1,b1]为初始含根区间(假设q(tm)>0)。

一般地，如果已计算得到含根区间[ak,bk](k=1,2,…)，则令ffk+1=(ak+bk)/2，若

终值f*=(ak+bk)/2，设真实值为f0，对于给定精度|f*-f0|<ε，实际计算是所采用的终止原则为

bk-ak<2ε=10-p

(21)

取ε=10-p/2，其中p为正整数，则有

(22)

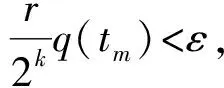
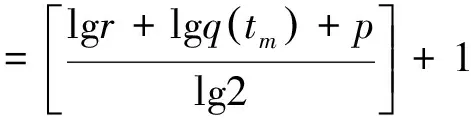
(23)

这里的[]为取整符号。

可以看到，这种步步迭代算法增加的计算量主要取决于每一次K*的大小，这又与初始含根区间的边界值密切相关，而结果的精确性主要是由ε来决定的。

3 仿真算例及抗噪性能

仿真计算模型为一根长度为0.68 m，截面尺寸为0.04 m×0.008 m的两端简支矩形截面梁，弹性模量70 GPa，材料密度2 700 kg/m3，划分为20个有限元单元。利用实验测得系统固有频率和模态阻尼比，调整建立的理论有限元模型，如表1所示。在第10自由度上加载f=10sin(4πt)N的正弦力，已知数据为第8自由度上的加速度响应。

设激励时间为t，计算次数为i，计算结果表明Wilson-θ反分析法不是一种成熟稳定的方法，不同的时间步长对计算结果有很大的影响。从图1(a)，(c)，(e)可以看出，无论时间步长的取何值，当计算次数达到一定数量，结果都会出现发散。而如图1(b)，(d)，(f)所示，修正计算后，识别结果收敛到了真实力。

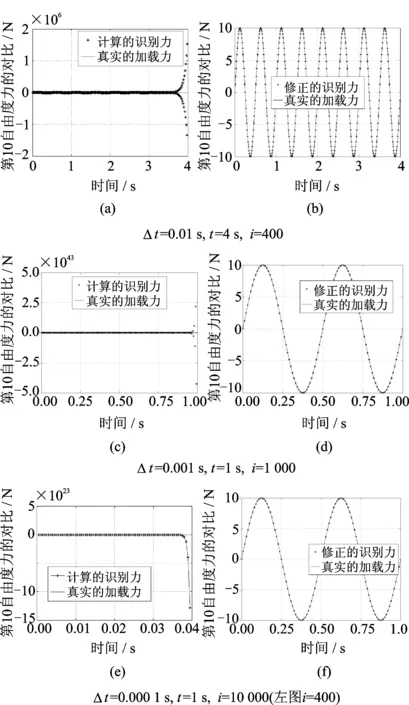
图1 不同时间步长下识别的载荷

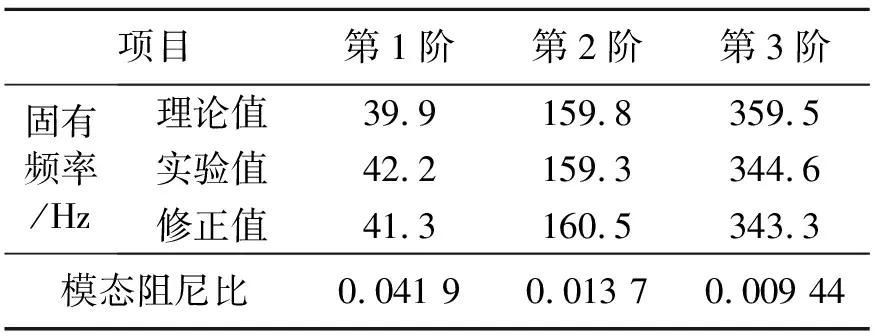
表1 模型参数

在实际工程问题中，噪声的影响是必须要考虑的，一个真正成熟稳定的算法应该具有不错的抗噪性能。在上述算例中，对于已知的加速度响应数据，加入5%的随机噪声(Δt=0.01 s)。图2对比了二分法迭代修正前后对于噪声的不同表现。可以看到修正后的识别力更能反映真实情况，而且发散的趋势明显减小。

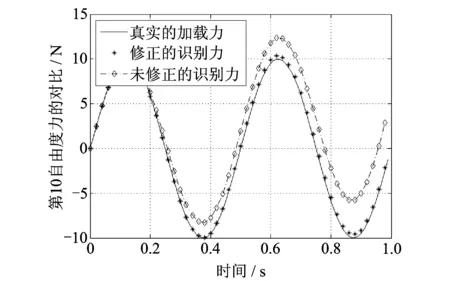
图2 加噪后的识别载荷(5%噪声水平)

下面考察对于实际工程问题中更常遇到的几种常见加载形式下的抗噪能力，图3显示了冲击载荷、方波、三角波和锯齿波的识别结果(Δt=0.001 s)。可见，由于噪声的影响，加载函数平直段的识别效果较差(如冲击载荷与方波载荷)，曲线段也不如没有噪声时光滑，但是基本能够反映出所加载荷的情况，是可以接受的识别结果。以组合三角函数波的长时间识别为例，加入5%的随机噪声，图4放大显示了尾段2 s的识别情况，可以看到在半分钟内，虽然些微不收敛，但该修正算法依然可以保持良好的稳定性(Δt=0.001 s)。

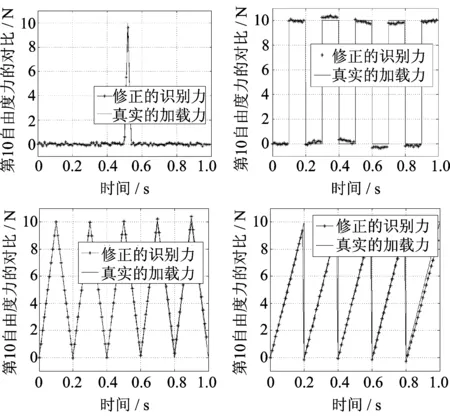
图3 不同形式加载下的识别结果(5%噪声水平)

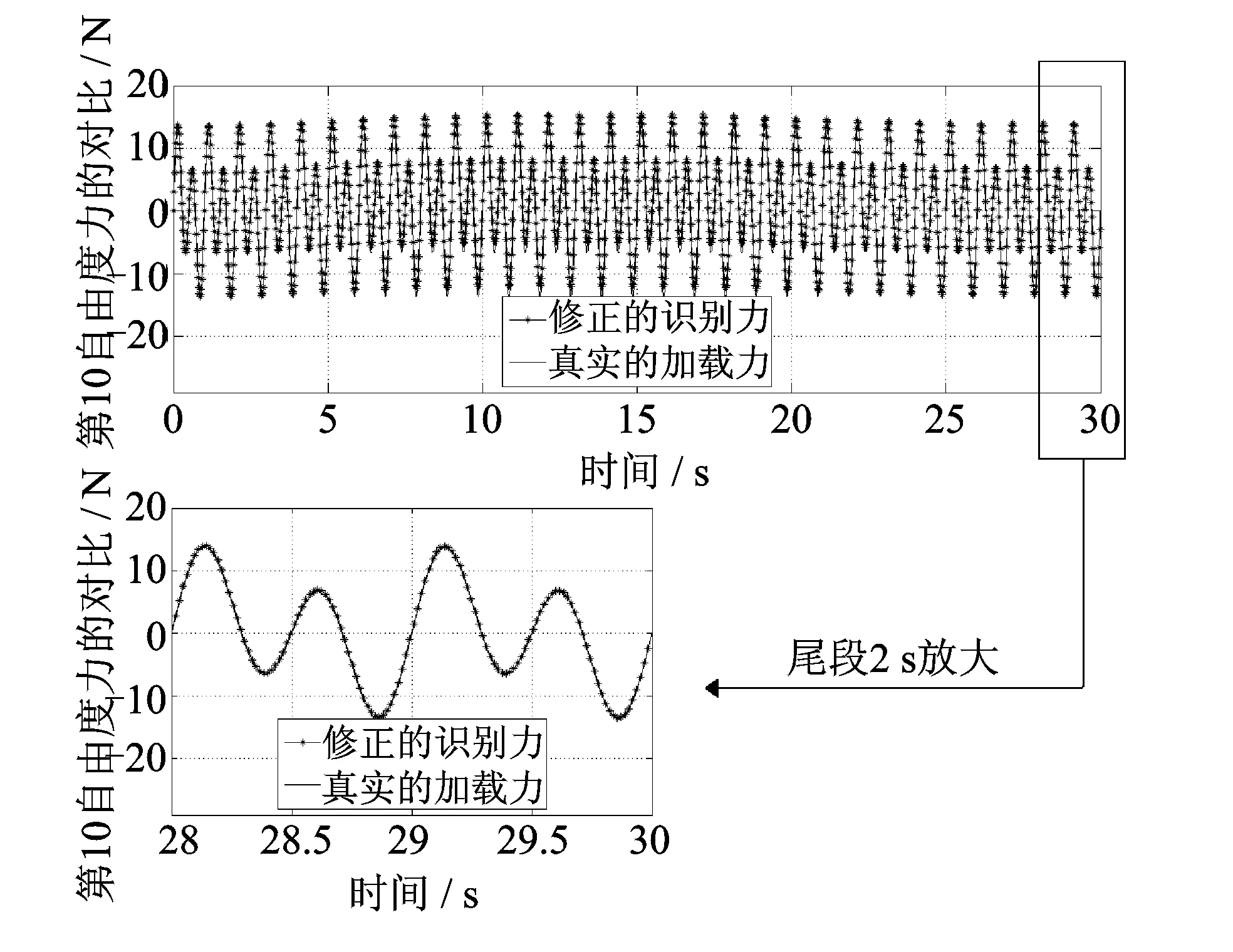
图4 长时间激励识别结果(5%噪声水平)

4 实验验证

实验模型与上述仿真模型一致，主要仪器设备有：Agilent35670动态信号分析仪，HEW 系列高性能电磁激振器，ICP型加速度传感器以及力传感器等。

在第6个结点上加载频率为16 Hz的正弦力，采样率2 048 Hz。测得第13和17结点上的加速度响应，应用上述修正算法分别得到两条识别力曲线，与实际所加载荷比较，结果如图5所示。

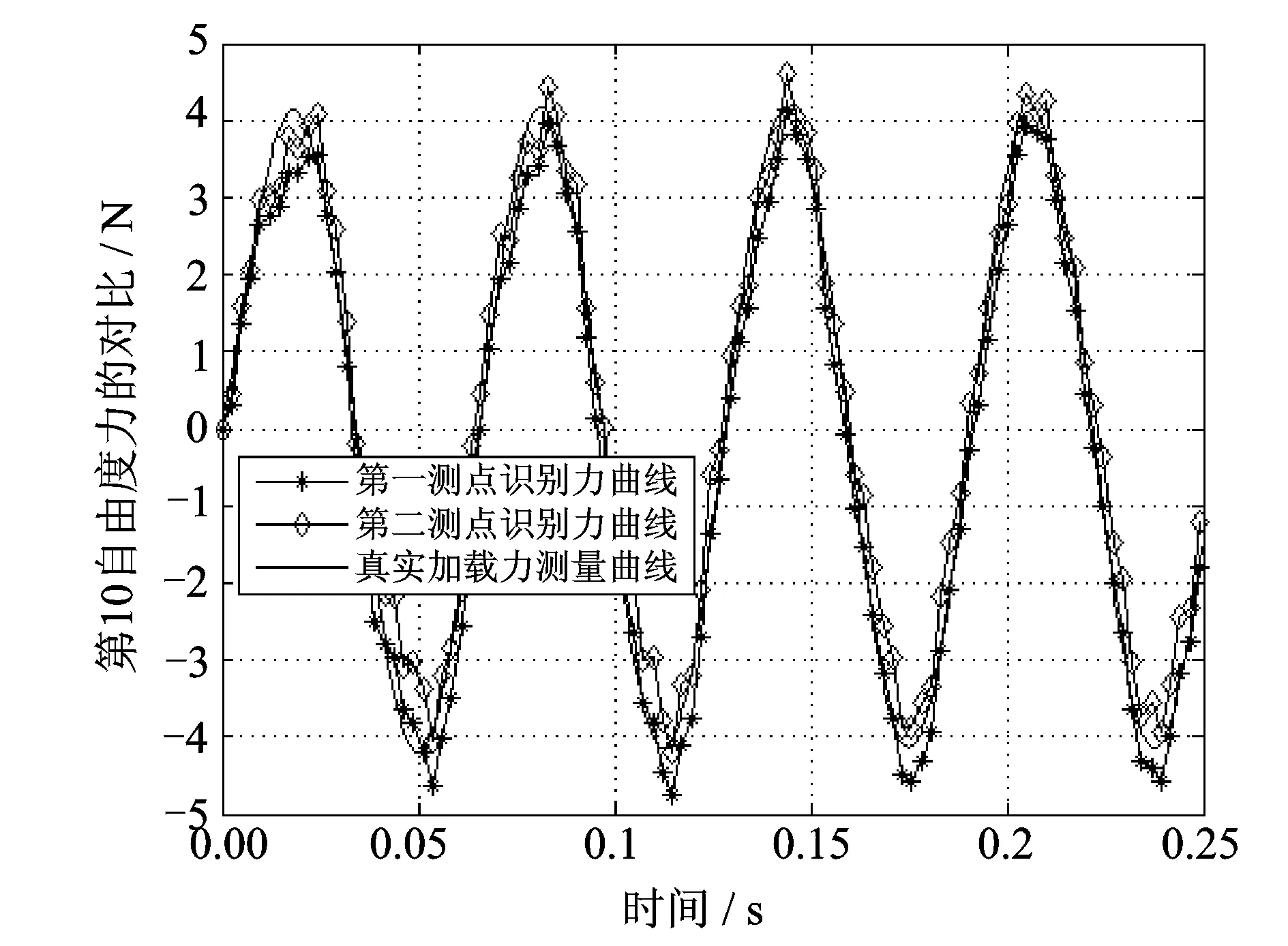
图5 实验数据得到的识别结果

为进一步分析实验结果数据，对于其中较为光滑的最后一个周期作分析，设每一个采样点的误差值为ei(i=1,…,N。其中，N为一周期内采样点数)，这些数组成了一个随机序列

(24)

式中fi为实际所加载荷，pi为计算识别力，fpeak为加载的峰值。该随机序列的统计数据如表2所示。

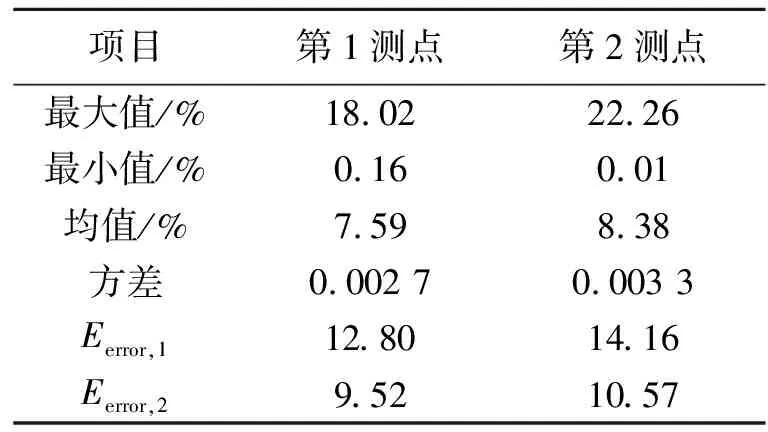
表2 误差统计

其中

(25)

(26)

不同于式(24)，这两个误差计算公式主要反映了每一个时间点的实时误差，式(25)是常用的误差计算公式，式(26)是一种考虑权重的误差计算方法，在接近零点时由于fi很小，其实时误差可能会很大，但是这个点的误差参考价值并不大，加权计算可以有效避免这个问题。

从图5来看，两条识别曲线都与实际所加载荷波形基本吻合，第1测点的识别力曲线要优于第2测点，虽然有个别点误差较大，但总体并没有发散的趋势。造成实验出现误差的原因有多种，计算所用的有限元模型与实际模型并不完全一致，实验仪器和设备的不稳定，以及布点位置不准确等都会造成计算值的偏差和波动。从实验可以看到，该修正算法计算结果基本反映了真实情况，误差在可以接受的范围内。

5 结 论

在以往一步到位直接得到载荷的算法中，难免会遇到误差累积的问题，本文提出了一种载荷识别的新思路，即在每一个时间步长内部迭代修正。典型载荷的仿真和实验结果表明，该修正算法可以有效的减小由于累积误差导致的发散，得到收敛的识别结果，并且有着理想的抗噪性能，具备一定的工程实用价值。

参考文献：

[1] 张方, 秦远田, 邓吉宏. 复杂动态载荷识别技术研究[J].振动工程学报, 2006, 19 (1): 81—85.Zhang Fang, Qin Yuantian, Deng Jihong. Research of identification technology of dynamic load distributed on the structure[J]. Journal of Vibration Engineering,2006,19 (1):81—85.

[2] 秦远田. 动载荷识别应用技术研究[D]. 南京: 南京航空航天大学, 2007.Qin Yuantian. Study on dynamic load identification applications [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2007.

[3] Matthew S Allen, Thomas G Carne． Delayed, multi-step inverse structural filter for robust force identification [J].Mechanical Systems and Signal Processing, 2008, 22:1 036—1 054.

[4] Fergyanto E Gunawan, Hiroomi Homma， Yuichi Morisawa. Impact force estimation by quadratic spline approximation [J]. Journal of Solid Mechanics and Materials Engineering, 2008, 2(8):1 092—1 103.

[5] Chen Tsung-Chien, Lee Ming-Hui. Determination of moving tank and missile impact forces on a bridge structure [J]. Defence Science Journal, 2008, 58(6): 752—761.

[6] Mao Yu-ming,Guo Xing-lin. Experiment study on dynamic force identification by a parameter estimation method [A]. Proceedings of the SEM Annual Conference [C]. Albuquerque,2009:1—4.

[7] 韩旭, 刘杰, 李伟杰, 等. 时域内多源动态载荷的一种计算反求技术[J]. 力学学报, 2009, 41(4): 595—602.Han Xu, Liu Jie, Li Weijie, et al. A computational inverse technique for reconstruction of multisource loads in time domain[J]. Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(4): 595—602.

[8] 高峰, 李德武. 运用振动反分析方法计算振动荷载[J]． 工程力学, 1999, 16(4):91—96.Gao Feng, Li Dewu. Evalution of dynamic loading by using the inverse analysis method in vibration[J]. Engineering Mechanics, 1999, 16(4):91—96.

[9] 姜金辉, 陈国平, 张方. 多点平稳随机载荷识别方法研究[J].振动工程学报, 2009, 22 (2): 162—167.Jiang Jinhui, Chen Guoping, Zhang Fang. Identification method of multi-point stationary random Load [J]. Journal of Vibration Engineering, 2009, 22 (2): 162—167.

[10] Lin Dong-Cherng. Input estimation for nonlinear systems [J]. Inverse Problems in Science and Engineering, 2010, 18(5): 673—689.

[11] Lin Dong-Cherng. Adaptive weighting input estimation for nonlinear systems[J].International Journal of Systems Science, 2012,43(1): 31—40.

[12] Ming-Hui Lee. Intelligent fuzzy weighted input estimation method for the input force on the plate structure [J]. Structural Engineering and Mechanics, 2010, 34,(1): 1—14.

[13] Lee M H, Chen T C. Intelligent fuzzy weighted input estimation method for the forces generated by an operating rotating machine [J]. Measurement, 2011, 44(5):917—926.

[14] 赵凤遥. 水电站厂房结构及水力机械动力反分析[D]. 大连: 大连理工大学, 2006.Zhao Fengyao. The dynamic identification of hydropower house structure and hydraulic machinery[D]. Dalian: Dalian University of Technology, 2006.