政策不确定性与股票市场波动溢出效应
陈国进
厦门大学 王亚南经济研究院,福建 厦门 361005
张润泽 姚莲莲
厦门大学 经济学院,福建 厦门 361005
近年来,学者已经逐渐意识到政策不确定性对金融市场产生的重要影响,政策的制定和变迁对资产价格的波动产生了关键性的作用。很多学者将中国的股市称为“政策市”,也足以见得政策不确定性对于中国股市的影响程度之大。反过来,股票市场映了经济的总体运行状况,因此长期以来被政策制定者作为判断经济走势和决策的重要依据。可见,分析政策不确定性与股票市场的波动溢出效应,既能更全面地剖析股票市场暴涨暴跌的原因,为股票市场的金融异象提供新的理论研究视角,又能为投资者和决策者的投资行为和宏观调控提供依据,具有很强的理论与现实意义。
一、文献综述
目前只有为数不多的学者从理论的角度研究政策不确定性与股票市场的关系,并且采用的分析方法大多基于一般均衡模型和动态最优化。如Croce et al.(2012)[1]、P'astor and Veronesi(2013)[2]等。从实证研究而言,Li and Born(2006)[3]运用GARCH模型发现在美国重要选举的前几周,尤其是不确定性较高的选举,股票市场回报往往会特别高。Goodell and Vahamaa(2012)[4]研究了在美国政治选举周期时的政策不确定性对VIX指数提取的股票市场隐含波动率的影响。Sialm(2009)[5]分别运用税收的时间序列变化和横截面变化的数据验证了税收的不确定性是否在资产定价中被估值,得出的结论是总估值水平与股票市场上征收的总的个人税负相关。Lam and Zhang(2013)[6]利用1995~2006年期间49个国家的面板数据和Fama-French的风险因子分析方法检验了政策不确定性对于国际股票市场的影响。
国内对于政策不确定性市场效应的研究还处于起步阶段,选取的研究角度一般是分析财政政策、货币政策工具本身对于股票市场的影响。陈其安等(2010)[7]利用GARCH模型实证研究了宏观经济环境、政府调控政策与中国股票市场波动性的关系。金雪军等(2014)[8]运用FAVAR方法分析了政策不确定性冲击对中国宏观经济的影响,其中简要证明了政策不确定性通过预期效应促使股票价格的下跌。
现有对股市和政策不确定性之间关系的考察主要从以下两方面展开:一是从收益率角度考察政策不确定性对股市的风险溢价效应;二是从波动率角度,考察政策不确定性对股市的单向波动溢出效应然而,不仅政策不确定性能够对股市的波动产生溢出效应,股市波动率反过来也能影响政策的制定和变迁。在股市暴涨时,政府倾向于推行紧缩性的政策以使股市降温,而当股市暴涨时,政府又倾向于为投资者提供一定的看跌式保护。正是由于股市是经济的“晴雨表”,因此决策者在政策制定的过程中往往都将股市的表现作为重要的决策依据之一。由此说明股市和政策不确定性之间存在双向的波动溢出效应,而之前学者还鲜有对该现象进行深入的研究。
本文借鉴Baker et al.(2013)[9]最新提出的与经济相关的政策不确定性指标,弥补了学术界在政策不确定性代理变量选取上的不足,同时运用DCC-MGARCH模型和BEKK-MGARCH模型较为系统地分析了以下两个命题:第一,运用 DCCMGARCH模型考察了中国股市与政策不确定性之间的动态变化,说明两者间存在的内在关联性;第二,运用VARMA-BEKK-MGARCH模型具体分析股市与政策不确定性之间的双向波动溢出效应,并分析两者波动率之间的传导机制。上述分析在一定程度上弥补了国内外学界关于政策不确定性与股票市场波动性实证研究的不足。
三、研究方法
(一)序列的ARCH效应检验
大量学者已经证明股票市场收益率存在尖峰厚尾和波动率聚类现象,而政策不确定性尽管并非在市场交易中产生,但是其变化过程仍然近似地服从某种随机过程,因此与股票市场收益率特征具有很强的相似性。这使得经典计量理论中序列扰动项同方差的假设不再成立,而GARCH类模型能够很好地刻画序列的条件异方差特征。在运用GARCH类模型进行实证分析之前,首先需要对模型均值方程的残差进行ARCH效应检验。
(二)VARMA模型及条件MLE估计
VARMA(p,q)模型可以表示为:

而VAR模型则是对应于q=0时的简化的VARMA(p,q)模型。

其中L为滞后算子,则式(1)可以表示为Φ(L)Yt=φ0+Θ(L)θt(2)
对于VARMA(p,q)模型的参数估计可以采用条件MLE方法。该方法假定θ0=0,在这个假定下,式(2)可以改写为θt= ΦtY1-φ0+Θθt-1,可以递推地计算θt有:

因此,似然函数变为:
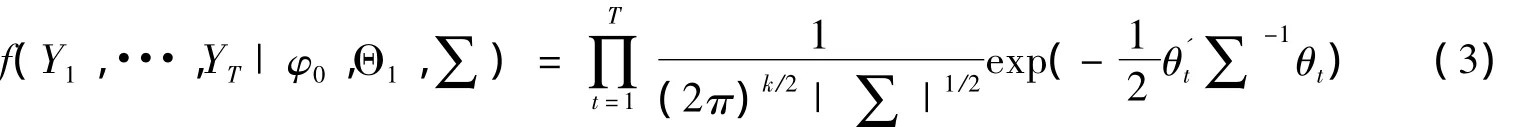
并据此得到参数估计。
(三)两序列动态相关性的DCC-MGARCH模型
首先分别对两序列建立GARCH(1,1)模型:
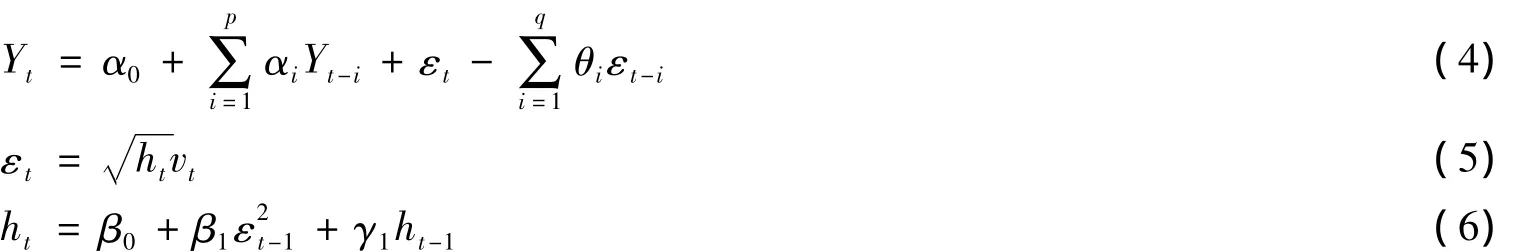
式(4)中变量含义同前所述,{vt}是均值为0、方差为1的独立同分布(iid)随机变量,ht是条件异方差。
以下式子中i=1,2,j=1,2,其中1表示股票市场收益率,2表示政策不确定性指标。定义 Rt为动态相关性矩阵,其元素 Qij,t可认为是序列 ri,t、EPUj,t的相关系数,变量均值接近于0,则
Qij,t+B(qij,t-1-),为非条件协方差。设 Qt=(qij,t)2×2,则由此得出两序列的条件方差协方差矩阵:Ht=DtRtDt=其中 Dt=Rt的元素 Q12,t的变化反映了两个序列之间相关性的动态变化。
(四)两序列波动溢出效应的BEKK-MGARCH模型
由于DCC模型只能用于研究序列波动率之间的动态相关系数,而无法判断波动溢出效应的传导方向,因此,需要利用BEKK模型来具体分析两序列之间波动溢出效应的传导路径。
BEKK(p,q)模型假设:

其中,C为下三角阵,Ai、Bj均为方阵。对于两变量的BEKK(1,1)模型来说,具体形式为:

将矩阵方程展开可得:

式(9)、(10)分别是股票收益率和政策不确定性序列的条件方差方程。在这两个式子中,第一个括号内的项为ARCH项,即前一期冲击εt-1对当期条件方差ht的影响;第二个括号内的项为GARCH项,即前一期条件方差ht-1对当期条件方差ht的影响。因此,系数a12和b12反映了政策不确定性波动对股市波动的溢出效应,而系数a21和b21反映了股市波动对政策不确定性波动的溢出效应。
四、实证研究
(一)数据描述
基于数据的可得性,本文中的样本使用的周数据,样本区间为1995年1月2日~2013年12月30日,共992个数据。
1.股票市场收益的度量指标。学术界普遍采用以连续复利计算的收益率作为股票市场收益的衡量指标。因此,股票市场收益水平选用连续复利计算的上证综合指数的周收益率,其定义如下:rt=ln(It)-ln(It-1),其中rt表示第t周的上证综合指数收益率,It为第t周最后一天的上证综合指数收盘指数。数据来源于雅虎财经数据库。
2.政策不确定的度量指标。政策不确定性度量指标选取的是EPU指数,该指数由三个部分组成。第一个部分是报纸中与经济政策不确定性相关的内容出现的频率。第二个部分是未来几年联邦将终止税法的可能性以及税法改变的福利效应;第三个部分是个人对未来通货膨胀和政府购买预测差异性。根据上述指标的均值和标准差对其进行标准正态化处理,并参照三个指标相应的概率分布赋予指标对应的权重,运用数据合成方法,构建了EPU指标。
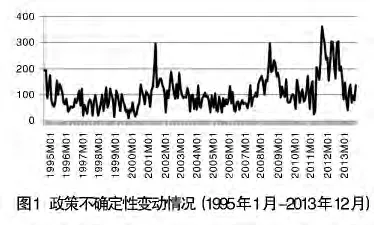
由于中国的EPU指标只有月度数据,考虑到EPU数据在短期内波动性较大的特征,因此,采用Cubic-match last方法进行低频数据向高频数据转换,并采用Quadratic-match average频率转换方法补充前几项缺失值。图1是1995年1月至2013年12月间政策不确定性的走势图,从图中可以看出,政策不确定性在整个样本期都有较大波动,具有很强的时变性特征。
(二)数据平稳性检验与HP滤波
1.平稳性检验。为避免序列的伪回归现象,对序列进行平稳性检验(表1)。

表1 序列的平稳性检验
ADF检验和PP检验结果显示,EPU序列和收益率序列在5%的显著性水平下均拒绝原假设“序列含有一个单位根”,可以认为两序列均为平稳序列。从趋势项检验结果来看,EPU序列的趋势项对应的t统计量显著,因此认为该序列含有趋势项。
2.HP滤波。对符合滤波条件的EPU序列进行HP滤波,滤波后的序列记为EPUC,并利用EPUC序列进行实证分析。由表2可以看出,经过HP滤波后的EPUC序列趋势项消失。

表2 EPUC序列的平稳性检验
(三)ARCH效应检验
为更好地对比分析ARCH效应,分4种情况对比序列的ARCH效应。情况1:不考虑股票市场和政策不确定性自身滞后项的影响,即认为两序列均满足Yt=α0+εt;情况2:只考虑两序列自身滞后项的影响,即两序列都独立地以Yt=α0+α1Yt-1+εt形式出现;情况3:只考虑两序列自身滞后项及残差滞后项的影响,即两序列都独立地以Yt= α0+ α1Yt-1+ εt- θ1εt-1形式出现;情况4:不仅考虑序列自身滞后项的影响,还考虑另一个序列滞后项影响,即两序列服从VAR(1)过程,表达式为:

分别对上述4种情况进行条件异方差的ARCH LM检验,得到了设定滞后p=3时的ARCH LM检验结果。

表3 ARCH效应检验结果
所有模型结果均显示,两个序列存在显著的ARCH效应,符合GARCH族模型建立的条件。
(四)股市与政策不确定性动态相关性分析
为了分析股市与政策不确定性之间的动态相关性,首先建立两个序列的GARCH(1,1)模型,综合考虑序列的自相关图、偏相关图、AIC、BIC准则以及模型拟合系数的显著程度,确定最优收益率序列均值方程为ARMA(1,1)过程,最优政策不确定性序列均值方程为ARMA(2,3)过程。对上述模型形式进行估计,估计结果如表4所示。表4结果表明,两个序列具有显著的ARCH效应,且ARCH项和GARCH项系数之和均接近于1,说明两序列的波动率存在聚集性和持久性的特征。

表4 GARCH(1,1)模型参数估计结果
其次,基于DCC模型进行极大似然估计,估计结果如表5所示。

表5 DCC模型参数估计结果
通过表5的系数A和B的参数估计值可以计算出股市收益率与政策不确定性之间的相关系数(图2)。从图2可以看出,两序列整体上呈现负相关的特征,并且相关性具有很强的时变性。
从统计结果来看,样本区间内上述动态相关系数的均值为-0.0124。对相关系数的显著性进行假设检验。原假设H0为动态相关系数均值为零,检验结果显示t值为-4.342422,p值接近于零,即拒绝原假设,说明两序列的动态相关系数显著异于零,进一步说明两序列之间存在显著的动态关系。
(五)股市与政策不确定性波动溢出效应分析
为了更好地揭示两序列之间的动态影响机制,采用 BHHH算法对BEKK模型进行极大似然估计。根据AIC和 BIC准则,得到均值方程为VAR(3)时AIC和SC值同时达到最小,故确定VAR(3)为最优模型。同时,为了更好地反映EPUC序列中存在的自相关现象,考虑VARMA(1,1)和VARMA(2,1)两种低阶的向量ARMA形式。原因在于,当涉及的时间序列是非季节性模型时,低阶的向量ARMA形式已经能够满足分析的需要,而高阶的向量ARMA形式大大地增加了参数估计的难度。因此,分别对VAR(3)-BEKK(1,1)、VARMA(1,1)- BEKK(1,1)和 VARMA(2,1)- BEKK(1,1)模型进行估计(表6)。

在条件均值方程中,所有模型都表明EPUC序列存在一定的自相关性,因此适合用VARMA模型刻画其特征。同时,VARMA(1,1)和VARMA(2,1)模型表明存在较为显著的股市收益率向政策不确定性的均值溢出效应,而政策不确定性向股市收益率的均值溢出效应不显著。
在条件方差方程中,a11、b11、a22、b22的估计值显著,这表明两序列都存在较大的波动率聚集现象,即在局部时间内,各期的波动率易于同时保持较高或较低水平。
对于两序列波动率的交叉项,a21、b21估计值分别在5%和1%水平下显著,说明股市上一期的ARCH冲击ε1,t-1和股市上一期的条件方差h11,t-1对政策不确定性当期条件方差h22,t有显著的影响。具体而言,假设t-1期股市上出现了一个冲击ε1,t-1,根据式(10),政策不确定性t期条件方差h22,t将增大。又由于股市自身的波动率聚类,根据式(9),股市t期的条件方差h11,t将由于t-1期的冲击而增大。因此,在t+1期,股市t期的条件方差h11,t将以b21的平方项增大政策不确定性条件方差h22,t+1。同时,由于b21平方小于1,因此该作用将以递减的程度持续下去。从而可以得出结论:中国股市的波动率冲击会通过h11对政策不确定性产生持久性的影响,该持久性具有拖尾的性质。
而从政策不确定性对股市的波动溢出效应来看,a12的估计值在5%的水平下显著,而b12的估计值在10%的水平下仍不显著,说明在短期内,政策不确定性上一期的冲击ε2,t-1对当期股市的波动有显著的影响,然而政策不确定性无法通过方差h22项对股市波动产生持久性的影响,从而说明政策不确定性对股市的波动溢出效应表现出截尾的特征。
为了从统计上验证两个序列波动溢出效应的真实性,本文分别做出以下三个联合假设检验。采用的方法为Wald检验法。Wald检验法的基本思想如下:设定原假设H0为 Rβ =r,构造统计量,其中q为约束条件个数,则拒绝域为

表7 波动溢出效应的检验
如表7所示,上述三个原假设都被拒绝,说明两序列之间确实存在波动溢出效应,由此证明了上文所述的波动溢出效应传导方向,即两序列之间存在显著的双向溢出效应。在具体方式上,股市对于政策不确定性的溢出效应具有长期拖尾的性质,而政策不确定性对于股市的溢出效应具有短期截尾的性质。两者之间的溢出效应并非严格对称。仅就波动率而言,股市对政策不确定性的影响大于政策不确定性对股市的影响。
五、基本结论
股票市场与政策不确定性的显著动态相关性说明股票市场与政策不确定性同时受到来自投资者层面和政府层面的共同因素的影响,而股票市场和政策不确定性本身所表现出的随机性特征决定了两者之间相关性的时变特征。
在波动率方面,两个序列波动率的双向溢出效应和不对称效应一方面说明了中国政府在政策制定上将股票市场短期和长期的波动性作为重要的决策依据,另一方面说明了中国投资者情绪存在强烈的非理性和投机成分,对于政策短期效应的过度反应和长期效应的反应不足造成政策不确定性只具有短期的溢出效应。
因此,中国在制定货币政策和财政政策等过程中,既要充分考虑股票市场波动性这一市场先行指标的预测作用,根据股票市场短期和长期的变化特征适时地调整政策变迁的强度和频率,降低股票市场对于经济的不利冲击。同时,面对投资者的非理性,应通过完善上市公司的分红制度以及股票市场的资本结构,引导投资者由短期的投机行为逐渐转向长期的投资行为,减缓股市在面临政策冲击时短期表现出的剧烈波动性,提高政策变动对股市的长期溢出效应。
[1]Croce,Maximiliano M.,Thien T.Nguyen,and Lukas Schmid,2012.The Market Price of Fiscal Uncertainty,Journal of Monetary Economics,401 -416.
[2]P'astor,ˇLuboˇs,and PietroVeronesi,2013.Political Uncertainty and Risk Premia,Journal of Finanial Economics,520 -545.
[3]Li,Jinliang,and Jeffery A.Born,2006.Presidential Election Uncertainty and Common Stock Returns in the United States,Journal of Financial Research,609 -622.
[4]JW Goodell,and S.V.Vahamaa,2013.US Presidential Elections and Implied Volatility:The Role of Political Uncertainty,Journal of Banking&Finance,1108 -1117.
[5]Sialm,2009.Tax Changes and Asset Pricing,American Economic Review,Vol.99,No.4:1356-1383.
[6]SS Lam,W.Zhang,2013.Does Policy Uncertainty Matter for International Equity Markets?Working Paper.
[7]陈其安,张媛,刘星.宏观经济环境、政府调控政策与股票市场波动性——来自中国股票市场的经验数据[J].经济学家,2010(2).
[8]金雪军,钟意,王义中.政策不确定性的宏观经济后果[J].经济理论与经济管理,2014(2).
[9]Baker,Scott,Nicholas.Bloom,and Steve Davis,2013.Measuring Economic Policy Uncertainty,Stanford University Mimeo.

