基于小世界效应的中国矿业上市公司关联性研究

安 静，安海忠,,

(1.中国地质大学(北京)外国语学院，北京 100083；2.中国地质大学(北京)人文经管学院，北京 100083；3.中国地质大学(北京)资源环境管理实验室，北京 100083；4.国土资源部资源环境承载力评价重点实验室，北京 100083)

在矿业行业包含的所有矿业企业中，各个企业之间存在着各种各样的关系，比如企业之间的借贷关系、供应链关系等，这种错综复杂的关系结构不仅关乎每个企业的生存，同时也和整个行业的发展密切相关。对此一些学者已经进行了相关的研究[1-2]。事实上，由于大部分矿业企业已经上市，这些上市的矿业公司不但在整个行业中的地位举足轻重，而且也关系到广大投资者的利益问题。因此研究矿业上市公司之间的关系具有重要意义。

在我国的矿业上市公司中，为了规避风险和获得稳定的利润，一个上市公司往往选择多种经营产品，这就使得它们之间的主营项目出现重叠交叉现象，而在市场经济的环境下，主营产品重叠的上市公司之间必定存在某种关联性，这种关联性体现在两个方面：一方面是竞争关系，因为从产业组织学可知,生产同质产品(包括有形产品和无形的服务)的企业的关系是竞争关系；另一方面也是命运共同体，因为当外界环境发生改变时，会对相关公司产生相同的影响。因此主营产品是公司之间联系的重要纽带。本文运用复杂网络方法，从两个上市公司之间所经营的共有主要产品的关系视角来研究矿业上市公司之间的关系特征，分析关系中是否存在小世界效应的特点以及这种特征对矿业上市公司的影响。而从理论上说，小世界特性有助于网络中信息的传递，会促进企业的发展。因此此项研究有助于矿业上市公司了解自身，不断发展和完善自己，更好地在越来越激烈的竞争中把握机遇，扩大可持续性发展潜力。

复杂网络是复杂系统的表象[3-4]，如果复杂系统中的个体表示成网络中的节点，个体之间的联系表示成网络的边，则现实中许多复杂系统都可以用复杂网络的相关特性进行描述和分析，比如社会关系网络，科研合作网络，演员合作网络，计算机共享网络，新陈代谢网络，万维网，城市交通网络以及电力网等都可以采用复杂网络进行研究。运用复杂网络的理论和方法来研究和解释社会经济中的各种关联性受到了学者的重视，文献利用复杂网络的理论及研究方法对中国股市网络进行了分析，发现该网络具有许多复杂网络的典型特性[5-6]。

1 数据与研究方法

1.1 数据来源

本文的数据来自我国证券公司的股票交易系统，它提供了许多上市公司的相关信息。在石油、有色金属、煤炭等板块中，选择了共125家的矿业上市公司，所涉及的公司列在表1中。在系统中提取这些矿业上市公司主营产品信息，这些公司经营的产品涉及矿产资源的开发、选矿、冶炼，各种稀有金属以及贵金属产品等及对矿产资源的深加工及相关服务，将产品归类80余种主营产品，采用的数据截至2012年9月30日。

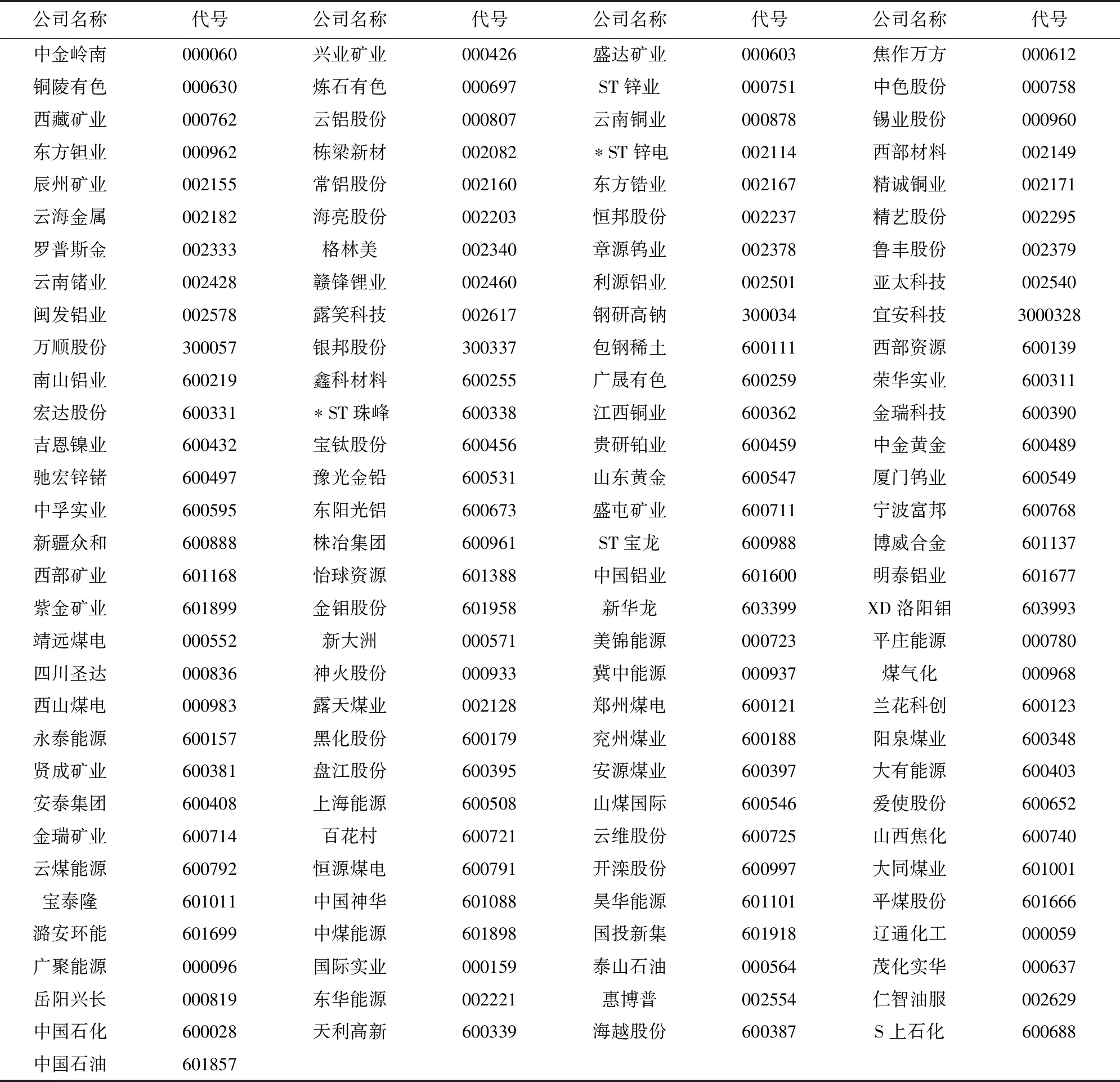
表1 125家矿业上市公司

1.2 小世界效应理论

复杂网络的典型特性之一就是小世界效应，它源于Milgram提出的六度分离推断[7]，即“世界上任何人之间都通过大约6步就可以建立联系”。Watts 等通过实验验证了这一假说，并于1998年与Strogatz将小世界模型引入对复杂网络的研究中，称为WS模型[8]。而后Newman和Watts对该模型进行了改进，建立了NW模型[9]。这两个小世界模型本质上是一样的，都反映了实际复杂网络的一个性质，即大部分节点只与它们的邻近节点相连，同时也有某些节点可与非邻近节点直接相连。研究一般会从两个角度来确定是否具有小世界效应，即平均最短路径长度和聚集系数。

小世界网络具有两个特性，第一个特性是连接各个节点之间最短的路径长度，网络的平均最短路径d定义为任意两个节点之间距离的平均值，见式(1)。

(1)

其中，N为网络中节点的个数，dij为节点i和节点j之间的最短的路径长度。

第二个特点是聚集系数C，节点的聚集系数是指与该节点相邻的所有节点之间连边的个数占这些相邻节点之间最大可能连边个数的比例，而网络的聚集系数则是指网络中所有节点聚集系数的平均值，它表示网络中节点的聚集程度，也就是说同一个节点的两个相邻节点仍然是相邻节点的概率有多大，它反映了网络的局部特性。一般情况下中心性较大的上市公司出现的波动会对其它公司的经营产生一定影响，其影响力的大小与所成网络的聚集程度相关。用ci表示节点i的聚集系数，假设对节点i来说，如果有ni条边和其它mi节点相连，Li代表这ki个节点之间的连线数量。则见式(2)。

(2)

网络的聚集系数C见式(3)。

(3)

式中N表示网络节点的数目。

Newman M E J、Watts指出由于以上的两个参数，高度结构化的网络有长路径和大的聚集度,而随机网络则有段路径长度和很小的集聚度[9]。一个小世界网络展示了与随机网络相近的路径长度，但却拥有高聚集度。设平均最短路径为L，网络中节点个数为N，网络节点的平均度为k，对于“小世界”网络，则有式(4)。

L≈lin(N)/lin(k)

(4)

针对网络小世界特性的研究最早主要是通过对网络的拓扑结构、集聚系数和平均路径长度的观察或者利用聚类系数与平均路径长度的比值来确定网络的小世界特性的。

1.3 网络模型构建

以表1中的矿业上市公司为节点，根据两个矿业上市公司是否有相同的主营产品来构建上市公司是否有边的关系，这一过程可以通过把反应每个公司所包含的主营产品的二部图(图1)转换成公司与公司之间关系的一部图(图2)。

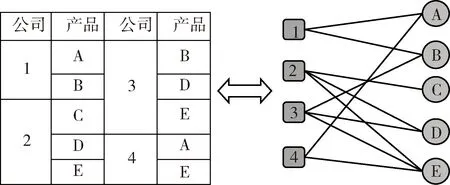
图1 公司与产品关系二部图

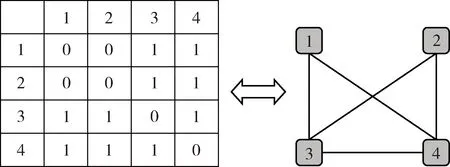
图2 公司与公司关系一部图

按照上述原理利用UCINET 6.0由图1和图2可以得到125家上市的矿业公司的基于主营产品关系网络。

2 实证分析

2.1 计算结果

根据125家矿业上市公司的关系矩阵，利用软件UCINET 6.0分别计算网络的平均最短路径的长度和聚集系数(表2)。

1)平均路长

Average distance=1.000

Distance-based cohesion (“Compactness”)=1.000

(range 0 to 1；larger values indicate greater cohesiveness)

Distance-weighted fragmentation (“Breadth”)=0.0

以上的计算结果说明网络平均最短路径长度为1，并且基于距离的凝聚系数也为1，距离权重段为0，路径很短，具有显著的小世界特性。

2)聚类系数

Overall graph clustering coefficient：0.818

Weighted Overall graph clustering coefficient：0.740

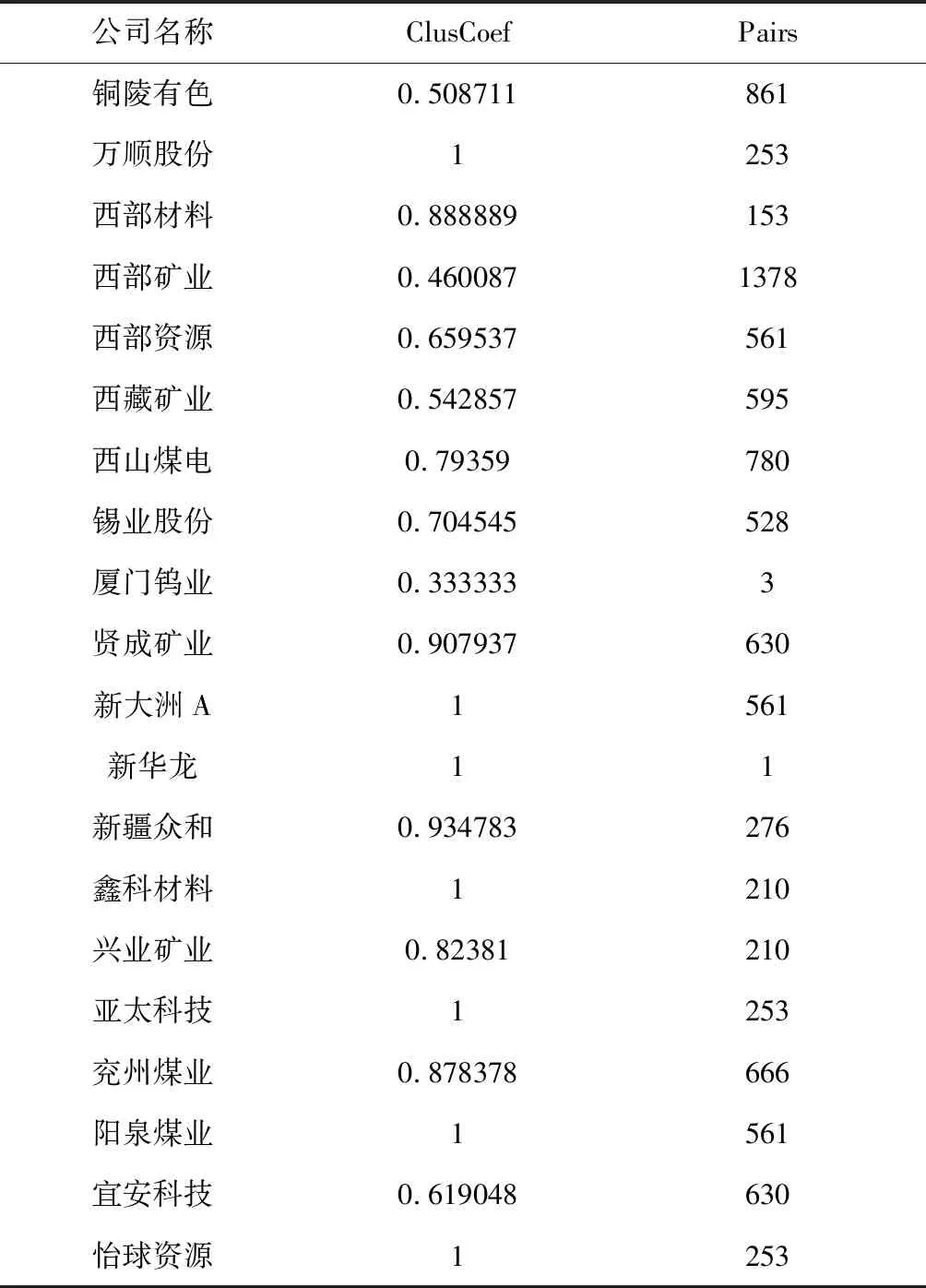
表2 节选整体中一段节点的聚集系数

2.2 结果分析

聚集系数表示网络中点间相互连接的情况。集聚系数的取值范围为[0,1]，当集聚系数取值为 1 时，表明网络中任意两点之间都有连接；当集聚系数取值为 0 时，表示网络中不存在三个点相互完全连通的情况。平均路径长度指网络中所有点相互之间距离的平均数。它反映了网络中各企业信息传递的效率。取值越大，效率越低；反之则效率越高。上述相关数据分析表明，基于相同主营产品的矿业上市公司的关系网络中，平均最短路径为1远小于网络规模125，由此可以证明矿业上市公司具有小世界网络的特征，网络中的上市公司形成“抱团”和“桥接”现象，抱团特征会增进上市公司之间的合作，同时促进相互之间的信任；而桥接特征会是上市公司之间的距离拉近，使上市公司更容易获取网络中其他上市公司的信息。而聚集系数接近1，总体显示聚集度非常高，连边数也非常多，也证明了基于主要产品的矿业上市公司之间具有明显的小世界效应特征，这说明在众多的矿业上市公司中，从一个公司到达另一个公司的联系只用很短的路径就能达到，也就是说一个公司对另外公司的影响力，很快地就能传达到另一个公司。从高度的聚类和上市公司众多的关联边数验证了我国矿业上市公司之间存在高度聚类的特征。

3 结论

本文基于主营产品对我国125家矿业上市公司的关联性进行了研究，按照各个上市公司重叠的主营产品构建上市公司之间的网络结构关系图，并通过计算相关数据验证了矿业上市公司关联性网络系统具有小世界效应的特征。这种高度聚类性从另一个方面揭示了矿业上市公司之间的关联性很强，相互之间关联密切，彼此的影响较大。而上市公司之间的联系越紧密，就越有利于各种相关信息的交流和融合，而不同的上市公司所拥有的信息有可能通过合作行为得到高频率深层次的交流，有利于整体行业的共同发展，同时也有助于各个上市公司做到知己知彼，有效地进行相关调整以提高公司利润并不断增进可持续性发展。

[1] 张昕瑞，王恒山.复杂供应链网络结构模型研究[J].工业技术经济.2008，27(2),79-81.

[2] 丁青艳.复杂网络结构下供应链企业间合作关系研究[D].北京：北京交通大学，2012.

[3] Barabasi Albert-Laszlo，AlbertReka.Emergence of scaling in random networks [J].Science，1999，286(10)：509-512.

[4] Barabasi Albert-Laszlo，Albert Reka，JeongHawoong.Mean-field theory for scale-free random networks [J].Physics A，1999( 272)：173-187.

[5] 马兴福，王红，李园园.基于复杂网络的中小企业板股市网络特性分析[J].计算机技术与发展，2012,22(4)：172-175.

[6] 鲁巍巍，林正春.基于复杂网络理论的沪深A股分析[J].科学技术与工程，2009，9(11)：2859-2862.

[7] Milgram S.The Small-World Problem[J].PsychologyToday，1967(2)：60-67.

[8] Watts DJ,Strogatz SH.Collective dynamics of Small-World networks[J].Nature，1998，393(6638)：440-442.

[9] Newman M E J，Watts D J.Renormalization GroupAnalysis of the Small-World Network Model[J].Physics Letters A，1999，263(4-6)：341-346.