基于未确知测度理论的排土场滑坡风险评价模型

栾婷婷，谢振华，吴宗之，何娜，张雪冬

(1. 北京科技大学 土木与环境工程学院，北京，100083；2. 中国安全生产科学研究院，北京，100029)

露天矿排土场是堆放剥离废岩(土)的场所，可能引起滑坡、泥石流等灾害，关系到矿山安全生产、人民生命财产安全和环境保护等各个方面[1]。近年来，排土场滑坡事故多发。2008 年8 月1 日，太钢尖山铁矿发生特大排土场滑坡事故，造成巨大的生命财产损失，再次警醒人们要关注排土场的滑坡灾害。目前，对于排土场稳定性的研究仍未形成一套较成熟的理论。相关的研究多借鉴矿山边坡稳定性研究的成果来开展。在边坡研究中，祝玉学[2]将可靠性理论引入岩质边坡稳定性分析中，薛新华等[3]提出一种判定边坡稳定性的模糊神经网络模型，谢全敏等[4]为评价多种因素对边坡稳定性的影响，提出岩体边坡稳定性灰色聚类空间预测方法。边坡稳定性评价的难点在于影响因素的复杂性和不确定性，因此，为使评价结果更加符合实际情况，需要采用适当的方法处理这些未确知信息。未确知数学理论[5]是有别于灰色理论和模糊数学的一种新的不确定性方法。刘开第等[6]将未确知测度评价模型应用于城市环境质量评价，并与模糊综合评判、灰色聚类分析、物元分析、BP 人工神经网络等评价方法比较,认为未确知测度评价模型的结果更合理。未确知测度模型也被成功运用到其他风险评价领域[7-9]。本文作者将应用未确知测度的模型，通过信息熵理论确定影响因素的权重，以便对露天矿排土场的滑坡进行风险评价。

1 未确知测度理论

设某个评价对象有m 个评价因素，用X1, X2, …,Xm表示，则评价对象空间X ={X1,X2,…,Xm}；某个评价因素有n 个评价指标，用I1, I2, …, In表示，则指标空间为I={I1,I2,⋅⋅⋅,In}。若xij表示第i 个评价因素Xi关于第j 个评价指标Ij的测量值，对xij有p 个评价等 级 C1, C2, …, Cp， 评 价 空 间 记 为 U ，U={C1,C2,⋅⋅⋅,Cp}。设第k 级比第k+1 级安全程度高，记 为Ck＞ Ck+1， 若C1＞C2＞⋅⋅⋅＞Cp， 则 称{C1,C2,⋅⋅⋅,Cp}是评价空间U 的1 个有序分割类[8-9]。

若uijk=u(xij∈Ck)表示测量值xij属于第k个评价等级Ck的程度，且u 满足：

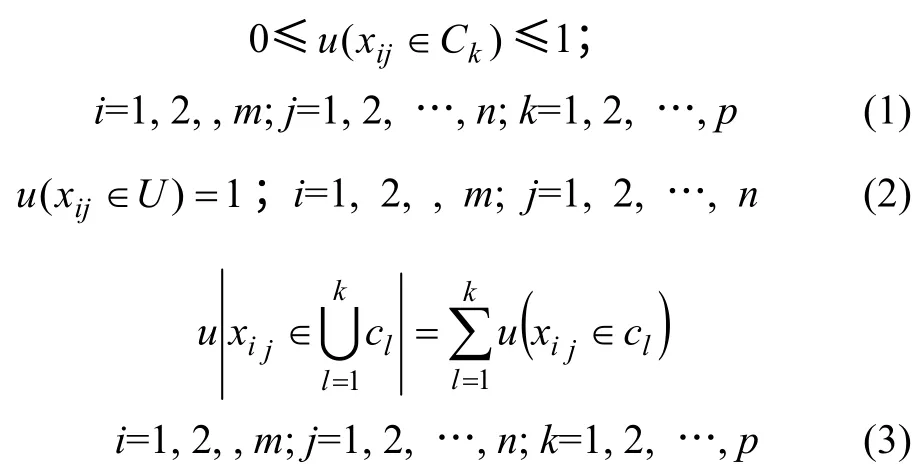
则称u 为未确知测度，式(1)称为测度的非负有界性；式(2)称为u 对评价空间U 满足归一性；式(3)称为u对评价空间U 满足可加性。上述3 条关于测度的限制条件是必须恪守的准则，有悖于其中任何1 条，其正确性都是值得怀疑的。在测度u 前冠以“未确知”是由于决策者经常是在信息不够完整的条件下构造测度函数，因此，除了必需的先验知识外，还包含着决策者个人的偏好、需求等主观因素。

1.1 构造单指标未确知测度

根据未确知测度的定义，构造单指标测度函数：u(xij∈Ck)( i=1, 2, , m; j=1, 2, …, n; k=1, 2, …, p)以便求出某评价因素Xi的各指标测度值uijk，则称各指标测度值uijk构成的矩阵(uijk)m×p为单指标测度评价矩阵。

根据具体问题的特征以及对状态变化的剧烈程度的认识，分别采用直线、二次曲线、正弦曲线和指数曲线等不同曲线连接，以构造测度函数的具体表达式。但不管采用什么形式的模拟函数，“非负、归一、可加”的限制条件是必须被满足的，否则，就不是严格测度意义下的测度。直线型未确知测度函数是应用最广、最简单的测度函数。

1.2 指标权重的确定

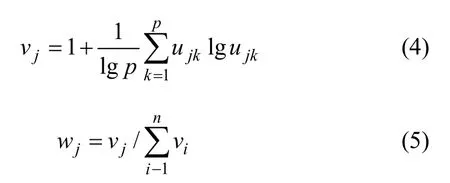
由于单指标测度评价矩阵是已知的，可根据式(4)和(5)求得各指标的权重 wj。

1.3 多指标未确知测度

若 wj为评价指标 Ij的权重，则存在 uik满足：

那么，向量uik=(ui1,ui2,…,uip)为 Xi多指标综合测度评价向量。

1.4 置信度识别准则

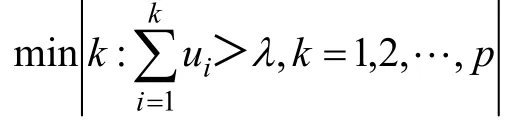
2 露天矿山排土场滑坡评价指标体系建立

排土场滑坡在排土场灾害中最普遍。由于影响排土场滑坡的因素很多，本课题组在对马钢姑山排土场、首钢水厂铁矿排土场、太钢尖山铁矿排土场、首云矿业排土场等典型露天矿排土场进行现场调研，对国内外部分露天矿山排土场典型滑坡事故进行案例分析，同时借鉴相关文献的研究成果[12-15]的基础上，建立排土场滑坡三级评价指标体系，如表1 所示。该评估指标体系包含地质因素、工程因素、气象因素和环境因素这4 个二级指标，以及地基坡度I1、边坡高度I2、边坡角I3、防排水设施I4、爆破质点振动速度I5、日降雨量I6、月累计雨量I7、最大地震烈度I8；下游人数I9、下游财产I10、乱采乱挖I11共11 个三级指标。每个三级指标分为4 个评价等级，Ⅰ级、Ⅱ级、Ⅲ级和Ⅳ级，分别对应于{C1, C2, C3, C4}，表示发生滑坡的危险性极高、危险性较高、危险性一般和危险性较低。每级都有一个规定的数值区间，三级指标中，9 个定量指标和2 个定性指标，对于定性指标，先根据指标的分级标准，进行定性到定量的转化，如表1 和2所示。

根据前面单指标测度函数的定义和表1 中各评价指标的赋值标准，构建露天矿山排土场滑坡评价指标体系的各指标测度函数，选择直线型测度函数，如式(7)所示。

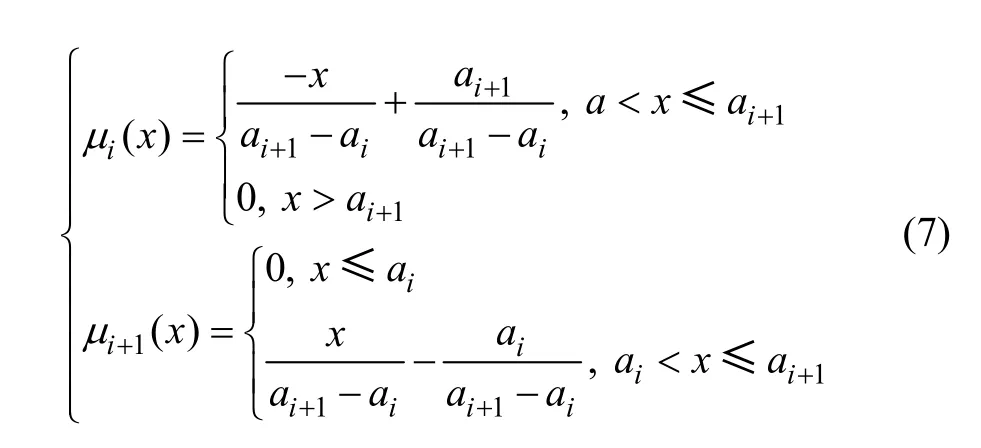
其中，ai是对象属性观测值分布区间上的点，假设在点ai的左测的属性值处于i 状态，当属性值从ai增加到ai+1的过程中，属性的i 状态的程度逐渐减弱，至ai+1时，i 状态的程度减为0，与此同时，当观测值从ai增加到ai+1时，属性观测值的i+1 状态程度由0 增加至1；则地基坡度、边坡高度、边坡角、爆破质点振动速度、日降雨量、月累计降雨量、最大地震烈度、下游人数和下游财产9 个定量评价指标的单指标测度函数依次如图1～9 所示。

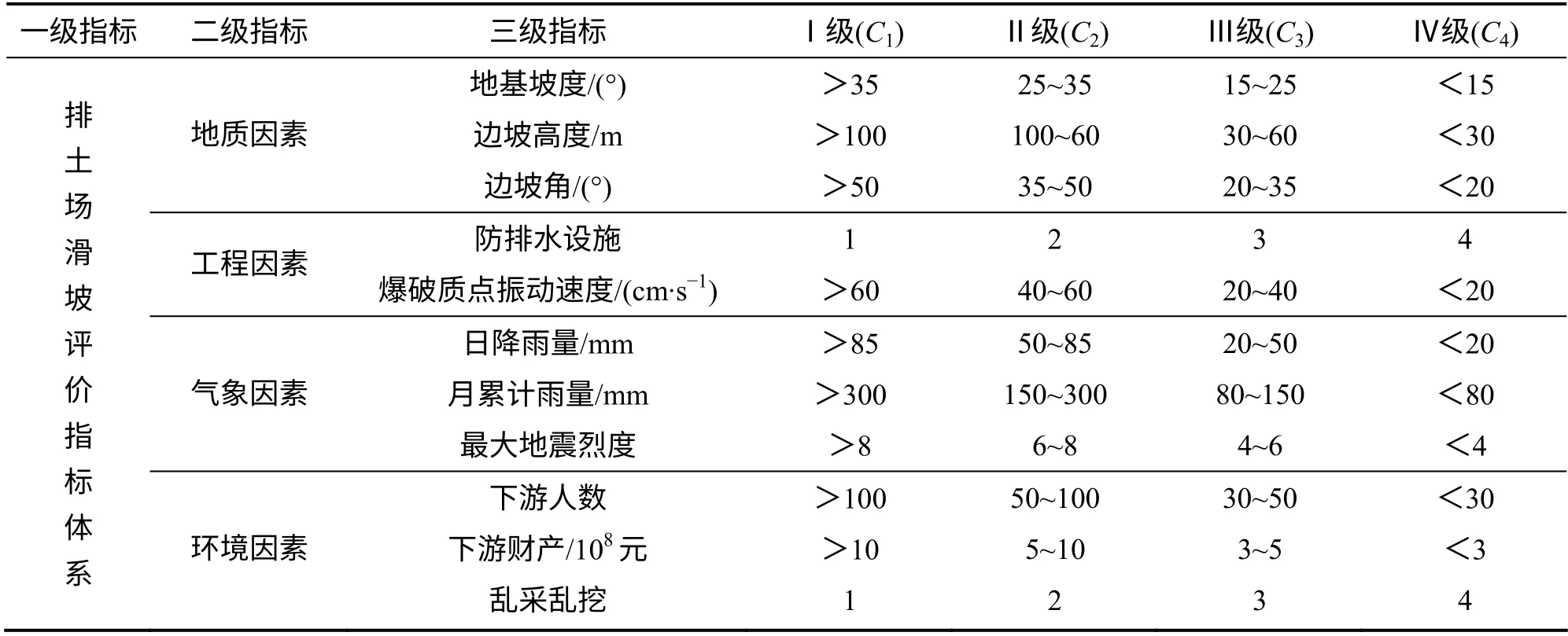
表1 排土场滑坡评价指标体系及对应的评价等级标准Table 1 Index system of waste dump landslide evaluation and corresponding classification criterion

表2 排土场滑坡评价中定性指标的分级标准Table 2 Classification criterion of qualitative indexes in the evaluation of waste dump landslide

图1 地基坡度的单指标测度函数Fig.1 Uncertainty measurement function of foundation slope

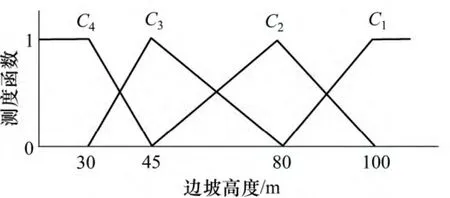
图2 边坡高度的单指标测度函数Fig.2 Uncertainty measurement function of slope height

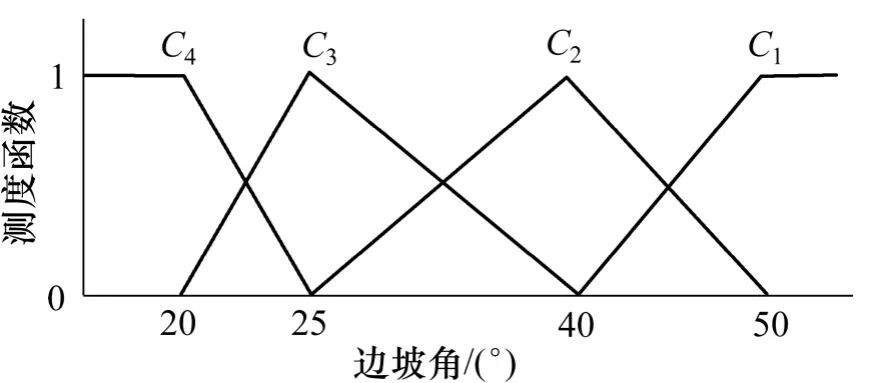
图3 边坡角的单指标测度函数Fig.3 Uncertainty measurement function of slope angle

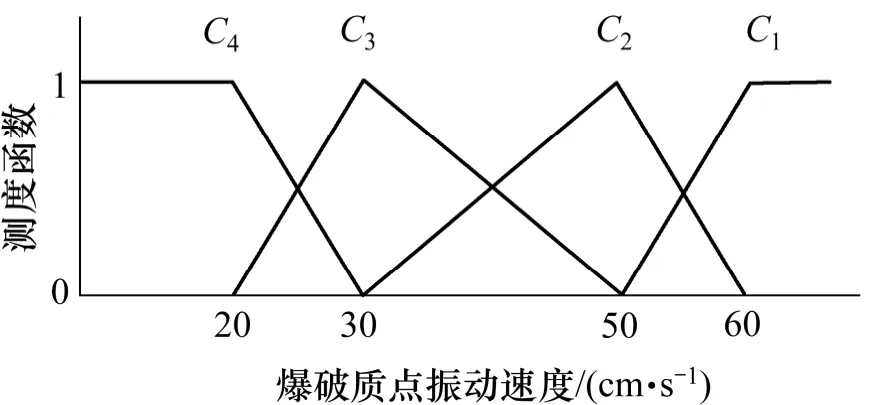
图4 爆破质点振动速度的单指标测度函数Fig.4 Uncertainty measurement function of blasting particle vibration velocity

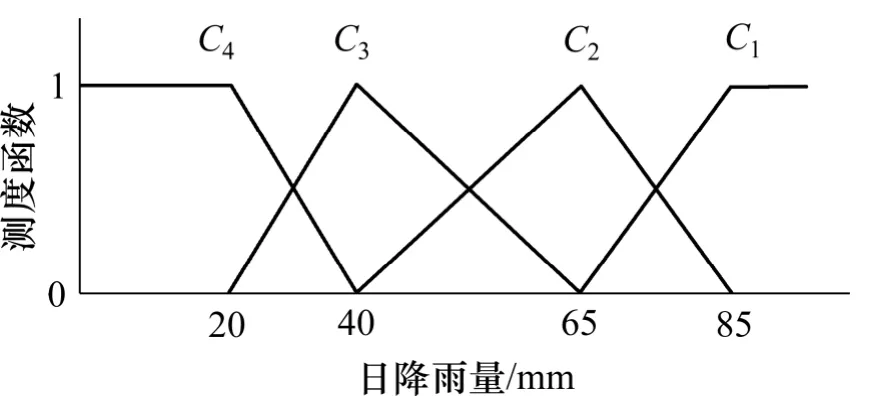
图5 日降雨量的单指标测度函数Fig.5 Uncertainty measurement function of daily maximum rainfall

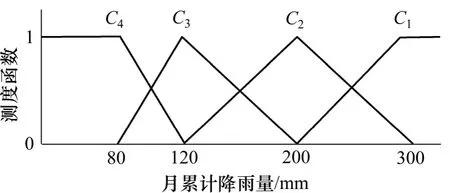
图6 月累计降雨量的单指标测度函数Fig.6 Uncertainty measurement function of monthly cumulative rainfall

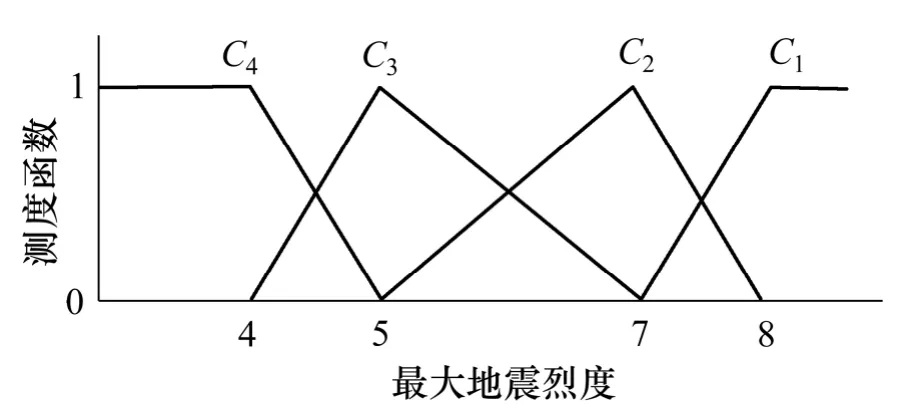
图7 最大地震烈度的单指标测度函数Fig.7 Uncertainty measurement function of maximum seismic intensity

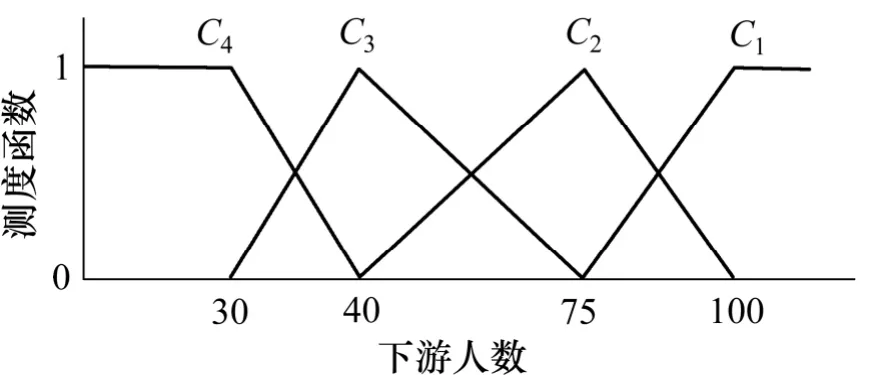
图8 下游人数的单指标测度函数Fig.8 Uncertainty measurement function of downstream population

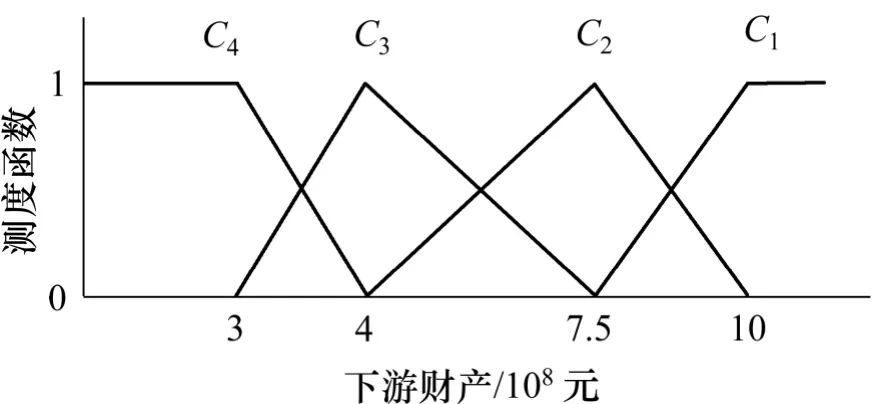
图9 下游财产的单指标测度函数Fig.9 Uncertainty measurement function of downstream property

3 案例分析

某露天矿山位于我国中部地区，矿山开采规模为每年9×106t，采剥量每年0.45×109t，排土场选择在露天采场的南部，到终了状态时形成最高近300 m 的覆盖式排土场。目前，该排土场分为2 个台阶，土场分段高度80～100 m，最终堆高达200～300 m。该排土场的边坡高度为45 m，边坡角为36°。该地区属大陆性半干旱高原季风气候，最高气温为36 ℃，最低气温为-21.4 ℃，年降雨量为440～600 mm，降水主要集中在7～8 月份，雨期60～80 d。在该排土场附近A 村和B 村有2 个雨量监测站，根据雨量站的监测数据，可获得日最大降雨量和月累计降雨量这2 个指标。该地区属于6 级地震烈度区，下游人数约100 人，下游财产大约3.5×108元，该排土场坡脚存在严重的乱采乱挖现象。

选取该排土场2008 年7 月中旬的指标，如表3所示。根据前面所建立的未确知测度理论模型，对这一时间段内排土场的滑坡危险性进行评价。

表3 某露天矿山排土场滑坡评价指标值Table 3 Index value of waste dump landslide evaluation in a certain open-pit mine

将表3 中排土场的各指标值分别代入图1～9 相应的单指标未确知测度函数中，定性指标的取值参见表1 和2，应用式(6)计算求得该排土场的单指标评价矩阵如下：

应用信息熵法确定指标权重，由式(4)和(5)求得露天矿山排土场评价指标权重为：W={0.074, 0.094,0.077, 0.133, 0.079, 0.066, 0.079, 0.066, 0.133, 0.066,0.133}。计算过程如下：

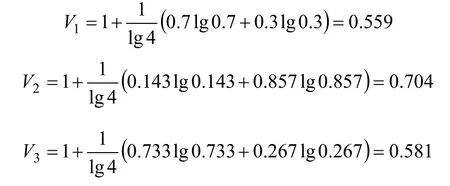
由求得的指标权重向量、式(6)和(8)，可求出露天矿山排土场滑坡的多指标综合测度评价向量：

取置信度λ=0.5，由多指标综合测度评价向量和置信度评价准则，从小到大有k0=0.266+0.307=0.573＞λ，即排土场的滑坡危险性等级为Ⅱ级；从大到小有k0=0.086+0.341+0.307=0.734＞λ，排土场的滑坡危险性等级也为Ⅱ级。由此可见， 2 次判别的结果一致，可判定该露天矿山排土场的滑坡等级为II级，即排土场发生滑坡的危险性较大，矿石企业要做好滑坡预防工作。

据调研资料显示，该排土场在此时确实存在着滑坡危险，因矿山有关部门没有重视此时的排土场稳定状况，导致该排土场在随后的半个月内发生了较大规模的滑坡灾害。这也验证了此方法的可行性和有效性。通过分析可知，地基坡度、边坡角、降雨量、下游人数、乱采乱挖等几个评价指标，对该排土场的滑坡影响很大，此次滑坡发生在7 和8 月份，正好是这一地区雨量比较集中的月份，从雨量站的监测情况来看，滑坡前的月累计降雨量已经有所升高；该排土场下游村民较多，一旦发生滑坡，后果极为严重，在排土场下部捡矿，掏空坡脚等现象严重，引起土场失稳。该矿山应加强排土场安全管理，清理排土场作业区和排土场边坡面违规乱采乱挖行为；尽量疏散排土场下游的村民，加强排土场日常监测与安全评价工作，对检查中发现的重大隐患，必须立即采取措施进行整改，并向安全生产监管部门报告。

4 结论

(1) 针对排土场滑坡过程中诸多因素的不确定性和复杂性，建立基于未确知测度理论的露天矿山排土场滑坡风险评价模型，运用信息熵理论确定评价指标的权重，采用置信度识别准则来评价滑坡的风险等级，为露天矿排土场的滑坡提供了较好的评价方法。

(2) 运用该模型对国内某露天矿山排土场滑坡危险性进行了定量评价，评价结果与该矿山的实际情况较吻合；为矿山企业的安全生产提供指导，对存在滑坡隐患的地方及时采取有效的预防措施，这也为排土场的安全管理提供了一种新思路。

(3) 为更好地验证模型的正确性和普适性，还需针对不同类型的露天矿山排土场滑坡进行调研分析，进一步完善排土场滑坡评价指标体系，使这种理论方法更科学合理地应用到实际中。

[1] 王运敏, 项宏海. 排土场稳定性及灾害防治[M]. 北京: 冶金工业出版社, 2011: 1-4.WANG Yunming, XIANG Honghai. Stability of dump and its disaster prevention and control[M]. Beijing: Metallurgical Industry Press, 2011: 1-4.

[2] 祝玉学. 边坡可靠性分析[M]. 北京: 冶金工业出版社, 1993:11-15.ZHU Yuxue. Slope reliability analysis[M]. Beijing: Metallurgical Industry Press, 1993: 11-15.

[3] 薛新华, 姚晓东. 边坡稳定性预测的模糊神经网络模型[J].工程地质学报, 2007, 15(1): 77-82.XUE Xinhua, YAO Xiaodong. A fuzzy neural network model for predicting slope stability[J]. Journal of Engineering Geology,2007, 15(1): 77-82.

[4] 谢全敏, 朱瑞赓. 岩体边坡稳定性灰色聚类空间预测方法[J].金属矿山, 1997, 6: 2-5.XIE Quanmin, ZHU Reigeng. The grey classification together method for space prediction of the stability of rock-mass slope[J].Metal Mine, 1997, 6: 2-5.

[5] 王光远. 论未确知性信息及其数学处理[J]. 哈尔滨建筑工程学院学报, 1990, 23(4): 52-58.WANG Guangyuan. Uncertainty information and its mathematical treatment[J]. Journal of Harbin Architecture and Engineering Institute, 1990, 23(4): 52-58.

[6] 刘开第, 庞彦军, 孙光勇, 等. 城市环境质量的未确知测度评价[J]. 系统工程理论与实践, 1999(12): 52-58.LIU Kaidi, PANG Yanjun, SUN Guangyong, et al. The uncertainty measurement evaluation on a city’s environmental quality[J]. Systems Theory and Practice Engineering, 1999,19(12): 52-58.

[7] 彭康, 李夕兵, 王世鸣, 等. 基于未确知测度模型的尾矿库溃坝风险评价[J]. 中南大学学报(自然科学版), 2012, 43(4):1447-1452.PENG Kang, LI Xibing, WANG Shiming, et al. Optimization model of unascertained measurement for dam-break risk evaluation in tailings dams[J]. Journal of Central South University (Science and Technology), 2012, 43(4): 1447-1452.

[8] 董陇军, 王飞跃. 基于未确知测度的边坡地震稳定性综合评价[J]. 中国地质灾害与防治学报, 2007, 18(4): 74-77.DONG Longjun, WANG Feiyue. Comprehensive evaluation on seismic stability of slopes based on unascertained measurement[J]. The Chinese Journal of Geological Hazard and Control, 2007, 18(4): 74-77.

[9] 阳富强, 吴超. 基于未确知测度理论的硫化矿石爆堆自燃危险性评价[J]. 中南大学学报(自然科学版), 2010, 41(6):2373-2380.YANG Fuqiang, WU Chao. Risk assessment on spontaneous combustion of sulfide ore dump in stope based on uncertainty measurement theory[J]. Journal of Central South University(Science and Technology), 2010, 41(6): 2373-2380.

[10] 曹庆奎, 刘开展, 张博文. 用熵计算客观型指标权重的方法[J]. 河北建筑科技学院学报, 2000, 17(3): 40-42.CAO Qingkui, LIU Kaizhan, ZHANG Bowen. Calculation method of objective index weight by entropy[J]. Journal of Hebei Institute of Architectural Science and Technology, 2000,17(3): 40-42.

[11] 郭章林, 雒燕. 未确知测度模型在城市燃气管道安全评价中的应用[J]. 中国安全科学学报, 2007, 17(7): 144-149.GUO Zhanglin, LUO Yan. Application of unascertained measure model to the safety evaluation of urban gas pipeline system[J].China Safety Science Journal, 2007, 17(7): 144-149.

[12] 杨胜利, 王云鹏. 排土场稳定性影响因素分析[J]. 露天采矿技术, 2010, 3: 4-6.YANG Shengli, WANG Yunpeng. Analysis of factors affecting dump stability[J]. Opencast Mining Technology, 2010, 3: 4-6.

[13] 马福恒, 何心望, 吴光耀. 土石坝风险预警指标体系研究[J].岩土工程学报, 2008, 30(11): 1735-1737.MA Fuheng, HE Xinwang, WU Guangyao. Risk early-warning index system for earth and rockfill dams[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(11): 1735-1737.

[14] 金海元. 岩石高边坡监测预警综合评价方法研究[J]. 长江科学院院报, 2011, 28(1): 29-33.JIN Hai-yuan. Research on comprehensive evaluation methods of monitoring and early-warning for rock slope[J]. Journal of Yangtze River Scientific Research Institute, 2011, 28(1): 29-33.

[15] 谢旭阳, 王云海, 张兴凯. 尾矿库区域预警指标体系的建立[J]. 中国安全科学学报, 2008, 18(5): 167-171.XIE Xuyang, WANG Yunhai, ZHANG Xingkai. Establishment of regional pre-warning index system for tailing reservoirs[J].China Safety Science Journal, 2008, 18(5): 167-171.